高速弹体冲击侵彻混凝土靶数值模拟分析
- 格式:doc
- 大小:546.00 KB
- 文档页数:10

弹体侵彻混凝土过程中炸药动态响应数值模拟贾宪振;李媛媛;郭洪卫;王建灵;高立龙【摘要】采用动力学计算程序AUTODYN对弹体侵彻混凝土过程进行了数值模拟.重点分析了弹体内部炸药所受压力的变化规律及装药与壳体之间的相互作用.数值模拟结果表明:弹体在侵彻过程中,装药前端主要受压缩作用,导致弹体前端的炸药产生明显的塑性应变.弹体尾部装药受到拉伸和压缩作用,并且装药和壳体尾部之间发生强烈碰撞,装药遭受明显的冲击作用.根据计算结果,侵彻型弹药设计应重点防护装药前端和尾部.%The process that a loaded projectile penetrated into a concrete target was simulated by using hydro-dynamic code AUTODYN. The study emphasis focused on the pressure imposed on the explosive charge and the interaction between the explosive charge and the projectile shell. Calculated results show that: the fore of the explosive charge mainly endures compressed effect which induces to plastic damage, and the tail of the explosive charge endures both compressed effect and tensile effect, as well as it is impacted by the tail shell which leads to strongly shock effect on the tail of explosive charge during the projectile penetration. According to our investigation, both the fore and the tail of the explosive charge need to be protected in the projectiles are used to penetration.【期刊名称】《科学技术与工程》【年(卷),期】2012(012)011【总页数】4页(P2528-2531)【关键词】爆炸力学;炸药;侵彻;动态响应;数值模拟【作者】贾宪振;李媛媛;郭洪卫;王建灵;高立龙【作者单位】西安近代化学研究所,西安710065;西安近代化学研究所,西安710065;西安近代化学研究所,西安710065;西安近代化学研究所,西安710065;西安近代化学研究所,西安710065【正文语种】中文【中图分类】O389;TJ55侵彻内爆型弹药可用于打击地下深层工事、混凝土/钢筋混凝土结构工事等军事目标[1,2]。

大质量高速动能弹侵彻钢筋混凝土的实验研究汪斌;曹仁义;谭多望【摘要】A metallic penetrator with the mass of 52 kg was designed by considering reasonably its structure and head shape. Based on the sub-caliber launch technology, the designed penetrator was accelerated to 1 300 m/s by a Davis gun to experimentally penetrate a six-layer reinforced concrete target with the size of 3. 0 m×3. 0 m×6. 0 m. The penetration experiment displays that the sub-caliber penetrator departed distinctly from the Davis gun, its flight attitude was stable, the attack angle was less than 2° , and the residual velocity was about 260 m/s after the penetration of the penetrator into the reinforced concrete of 6 m thickness. After the penetration experiment, the recovered penetrator was intact and only a little plastic deformation on the penetrator head. And the penetrator mass lost a-round 1. 2 percent, its length shortened 0. 7 percent, and the erosion phenomenon was unconspicuous.%设计了弹头形状和弹体结构合理的金属侵彻弹体,利用口径为320 mm的平衡炮,采用次口径加载技术,将直径为136 mm、长度为680 mm、质量为52kg的金属侵彻体加速到1 300 m/s,去侵彻尺寸为3 m×3 m×6 m的钢筋混凝土靶.实验结果表明:次口径弹托与弹丸完全分离,弹体飞行姿态稳定,飞行攻角小于2°,弹体侵彻6 m厚的钢筋混凝土后剩余速度约为260 m/s.实验后回收的金属弹体结构完整,仅弹体头部存在一定塑性变形,弹体质量损失约1.2%,长度缩短约0.7%,弹靶作用过程的侵蚀现象不明显.【期刊名称】《爆炸与冲击》【年(卷),期】2013(033)001【总页数】5页(P98-102)【关键词】爆炸力学;金属侵彻体;次口径发射技术;钢筋混凝土【作者】汪斌;曹仁义;谭多望【作者单位】中国工程物理研究院流体物理研究所冲击波物理与爆轰物理重点实验室,四川绵阳621900【正文语种】中文【中图分类】O385高速侵彻战斗部凭借高速度的优势能够对地下深埋、加固的重要军事目标进行毁伤打击。






混凝土-钢筋混凝土高速侵彻贯穿问题的数值模拟与试验探究关键词:混凝土;钢筋混凝土;高速侵彻贯穿;数值模拟;试验探究Numerical simulation and experimental study on high speed penetration problem of concrete/reinforced concreteAbstract: In view of the problem of high-speed penetration of concrete/reinforced concrete structure, this paper adopts the method of combining numerical simulation and experimental study to analyze the penetration situation under different materials and parameters. Firstly, a numerical model of high-speed penetration of concrete/reinforced concrete was established, and solved by finite element method. Through numerical simulation, the influence of material properties, penetration velocity, size and diameter of steel bars on penetration depth, impact time and energy absorption were studied. Secondly, a series of experimental schemes were designed. Through high-speed relative collision test, the performanceindicators such as penetration depth, deformation and crack development under different materials and parameters were measured and analyzed, and compared with the numerical simulation results. The results show that the main factors affecting penetration depth are penetration velocity and material properties, among which reinforced concrete has better protective performance; the main factors affecting impact time and energy absorption are the viscoelastic properties and size of materials, and it is suggested to increase the viscoelastic properties of materials and study the micro mechanism of impact damage. The research results of this paper have certain reference significance for improving the protection ability ofconcrete/reinforced concrete structures and optimizing design scheme.Keywords: concrete; reinforced concrete; high-speed penetration; numerical simulation; experimental stud。

中国地震局工程力学研究所硕士学位论文基于ANSYS/LS-DYNA的混凝土靶板侵彻问题的数值模拟与分析姓名:冯国忠申请学位级别:硕士专业:防灾减灾工程及防护工程指导教师:赵振东20060501中国地震局工程力学研究所硕士学位论文头部为半球头部为平头头部为锥形图4.1弹丸的头部形状4.2.2混凝土靶板模型本文中混凝土靶板首先采用*MATSOILCONCRETE关键字,可在一定程度上模拟破碎和崩落现象。
考虑到弹丸直径较小,影响范围有限,靶板尺寸取为40cm×40cm。
为简化计算,取1/4模型进行计算,用三维实体单元SOLIDl64划分网格,在对称面上施加对称边界约束,靶板边界施加固定约束。
混凝土的密度P=23×103堙/m3,泊松比V=O2。
在进行网格划分时,弹、靶作用范围内划分较细,其他部分划分较粗,这样既保证了计算精度,又能在一定程度上减少计算时间,充分利用计算资源。
划分网格之后靶板模型(如图4—2)的实体单元数目约为140000个,节点数目约为150000个。
4.2.3模型汇总图4—2土混凝二r靶板模型形状4数值模拟所用的实体模型总共九个:一个基本模型;根据混凝土的强度、板的厚度、弹丸着靶速度和弹丸头部形状,分别又取八个模型。
其中基本模型取混凝土板板厚80mm,混凝土的强度等级为C25(E=2.8×106Ⅳ/cm2),弹丸头部为半球状,弹丸着靶速度为1000m/s。
其他八个模型中混凝土板厚度分别取100mm和60mm,混凝土强度等级分别取C20(E=7.55×106N/cm2)和C30(E=3.00×106N/cm2),弹丸的着靶速度分别为1200m/s和800m/S,弹丸头部形状分别为平头和圆锥形。
为了便于和基本模型作比较,模型参数变化时只依次变化其中一项,其它参数与基本模型相同。
如板厚依次取100mm和60mm,其它参数不变,这样得到两个模型。

第28卷 第1期爆炸与冲击Vol.28,No.1 2008年1月EXPLOSION AND SHOC K WAV ES J an.,2008 文章编号:100121455(2008)0120033205弹体攻角侵彻混凝土数值模拟3马爱娥1,黄风雷1,初 哲2,李金柱1(1.北京理工大学爆炸科学与技术国家重点实验室,北京100081;2.西北核技术研究所,陕西西安710024) 摘要:利用L S2D YNA程序的用户自定义模型功能,在L S2D YNA程序中嵌入了用于描述混凝土及钢筋混凝土侵彻贯穿的动态损伤模型。
模型拉伸部分用Taylor2Chen2Kuszmaul(TC K)模型描述,体现了应变率对拉伸作用的敏感性;压缩部分则采用Holmquist2Johnson2Cook(HJ C)强度模型。
模型中考虑了拉伸损伤、压缩损伤、应变软化、静水压力效应以及应变率效应。
利用该方法对弹体攻角非正侵彻混凝土靶过程中的弹体变形、混凝土靶的损伤破坏、弹体的速度变化规律及弹体的变形进行了计算,并将计算结果与实验结果进行了比较,结果表明,采用该模型可以较好地模拟弹体非正侵彻混凝土过程。
关键词:爆炸力学;动态损伤模型;数值模拟;混凝土 中图分类号:O385;TJ4012.4 国标学科代码:130・3530 文献标志码:A1 引 言 混凝土目标侵彻和贯穿的数值模拟研究越来越受到重视,其中混凝土的动态损伤、失效模型以及开发相应的数值算法成为该方向的研究热点及难点。
目前应用较广的本构模型有Taylor2Chen2Kusz2 maul(TC K)[1]、Holmquist2Johnson2Cook(HJ C)[2]及Riedel2Thoma2Hiermaier(R H T)[3]模型。
TC K 模型以脆性拉伸损伤为主,损伤演化与平均拉应力、裂纹密度和体积应变率有关,该模型能较好地反映开坑、崩落以及裂纹扩展,但是未考虑材料的压缩损伤累积以及材料在压缩下的非弹性响应,致使预测的弹体剩余速度和侵彻深度偏差较大[4]。
弹箭与制导学报收稿日期:2010-03-30基金项目:重点实验室基金ZDKT 08-4-10作者简介:练兵(1980-),男,河南永城人,博士研究生,研究方向:弹药终点效应,E-mail:980205@高速长杆弹侵彻半无限混凝土靶深度分析模型练兵1, 2,蒋建伟1,樊虎2,门建兵1,王树有1(1.北京理工大学爆炸科学与技术国家重点实验室,北京 100081;2.空军驻襄樊地区军事代表室,湖北襄樊 441003)摘要:将高速长杆弹对半无限混凝土靶的侵入过程分为开坑、侵蚀阶段侵彻和刚体阶段侵彻。
侵蚀过程中计算长杆弹质量的减少量,侵彻过程中计算侵彻深度的增加量,对侵彻增量进行求和得到侵蚀状态侵彻总深度。
刚性阶段侵彻混凝土时,运用空腔膨胀理论计算侵彻深度。
应用分析模型对钨杆侵彻半无限混凝土靶深度进行了计算,与实验结果吻合较好。
关键词:高速;长杆弹;侵彻;混凝土 中图分类号:O313.4 文献标志码:ADepth Analysis Model of Penetration of high Speed Projectiles into Semi-infiniteConcreteLIAN Bing 1,2, JIANG Jianwei 1, FAN Hu 2, MEN Jianbing 1, WANG Shuyou 1(1. State Key Laboratory of Science and Technology of Explosion, BIT, Beijing 100081, China 2. Military Representative Office of Air Force in Xiangfan Area, Hubei Xiangfan 441003,China)Abstract : The penetration of long-rod projectiles into semi-infinite concrete was divided into cratey, penetration during eroding state and penetration during rigid state. The mass loss of projectiles was calculated in the eroding state while the increment of penetration of projectile was calculated in the penetration state. The total penetration depth during eroding state was obtained by summing the increment of penetration. When the projectiles penetrated concrete at rigid state, the penetration depth of projectiles was calculated based on cavity expansion theory. Penetration depth of tungsten alloy eroding projectiles into semi-infinite concrete was obtained by this analysis model and it was identical to the result obtained by the experiment. Keywords : high speed; long-rod projectile; penetration; concrete0 引言低速(着速小于1000m/s )弹丸对混凝土靶的冲击响应和破坏国内外进行了大量研究,空腔膨胀理论在低速侵彻问题上获得了较好的效果。
第28卷 第3期2008年06月弹 箭 与 制 导 学 报Journal o f P rojectiles,Ro cke ts,M issile s and G uidanceVo l.28 No.3Jun2008弹丸在不同速率下斜侵彻混凝土的数值模拟*冷冰林1,许金余1,陈 勇2,樊圣军3(1空军工程大学工程学院,西安 710038;295538部队,四川新津 611430;3西安建筑科技大学,西安 710055)摘 要:关于混凝土侵彻的研究一直是一个很活跃的领域,但由于整个侵彻过程时间极短,实验研究很难对侵彻过程进行全面准确的分析。
文中利用LS-DY NA3D有限元程序对弹丸在不同速率和着角下侵彻混凝土靶进行了三维数值模拟,得到了侵彻的整个图像和主要数据,分析了速率和着角与侵彻深度及破坏情况之间的关系。
研究表明:速率和着角对侵彻深度具有重要影响。
关键词:侵彻;数值模拟;速率;混凝土;弹丸着角中图分类号:O383.2 文献标志码:ANumerical Simulation of Projection Oblique Penetration ofConcrete Under Different VelocityLEN G Binglin1,X U Jinyu1,CH EN Yong2,FA N Sheng jun3(1T he Engineering Institute,A ir Fo rce Eng ineering U niver sity,Xi'an710038,China;2N o.95538U nit,Sichuan Xinjin611430,China;3Xi'an U niversity of A r chitecture T echnolog y,Xi'an710055,China)A bstract:T he research on projectile pene trating into concrete tar get is alway s a realm.But the time of the w ho le pene-tratio n process is very sho rt,w hich makes re sear cher s difficult to give the ge nera l and accurate analysis acco rding to ex-periment.In the paper,projectile penetr ating into concrete ta rge t wa s simulated under the different velo city and ang le of incidence,the whole picture of the penetr ation and main data wa s g ained.Acco rding to resea rch,velocity and angle of incidence plays an impo r ta nt par t in penetration depth.Keywords:penetration;nume rical simulatio n;velo city;concrete;pro jectile incidence1 引言混凝土作为一种重要的工程材料被广泛地应用于各个领域,如何有效地提高混凝土的抗侵彻能力,一直是结构工作者所关注的研究课题。
弹体侵彻混凝土靶板的数值模型作者:徐刚来源:《山东工业技术》2014年第12期摘要:基于细观力学原理,采用离散元软件PFC3D对Hanchak侵彻的部分试验进行了数值建模,使用平行粘结模型来模拟混凝土颗粒之间的接触力和力矩,并通过模拟弹体以不同速度侵彻混凝土靶板,将弹体在不同速度下剩余速度与试验值进行对比分析,数值模拟得到的结果相对于试验值的偏差都在允许范围内,验证了离散元侵彻模型和程序编写及算法的有效性。
关键词:混凝土;离散元法;侵彻1 引言近年来,国内外学者[1-3]在混凝土靶板侵彻过程分析方面,通过试验及理论推导得出了侵彻过程中阻力分析、侵彻深度等计算方法,并且大量的试验结果表明弹体侵彻或穿甲过程中均出现大小不一的偏转程度,但是无论是经验公式还是无量纲分析的理论模型,均将混凝土材料认为是均匀连续性介质,无参数涉及到弹体侵彻混凝土靶板过程中的偏转问题。
随着目前计算机技术的快速发展,数值模拟逐渐成为了解决复杂力学分析问题的主要手段之一,对于混凝土靶板侵彻问题的数值模拟分析也越来越多,同时也取得了一定的研究成果,但大部分集中在宏观层面上,且部分结果与试验结果存在较大的差距,为此本文采用PFC3D(particle flow code in three dimension)[4]建立混凝土靶板离散元数值模型。
2 离散元法的物理方程假设两个颗粒A和B接触,接触的两个颗粒可以视为一个弹性梁,梁的两端位于颗粒的中心,外力和外力矩作用于梁的两端。
梁的特征参数可以分为:(1)几何参数—长度(L)、横截面积(A)和惯性矩(I);(2)变形参数—杨氏模量(E)和泊松比(v);(3)强度参数。
2.1 接触刚度模型接触刚度是将接触力和相对位移通过力—位移法则联系起来,即:式中,是法向接触刚度,表征总的法向力与位移。
式中,是切向接触刚度,表征增量形式联系切向力与位移。
在离散元法中有两种接触刚度模型,即Hertz-Minlin接触刚度模型与线性接触刚度模型,接触刚度模型不同则接触刚度值亦不同。
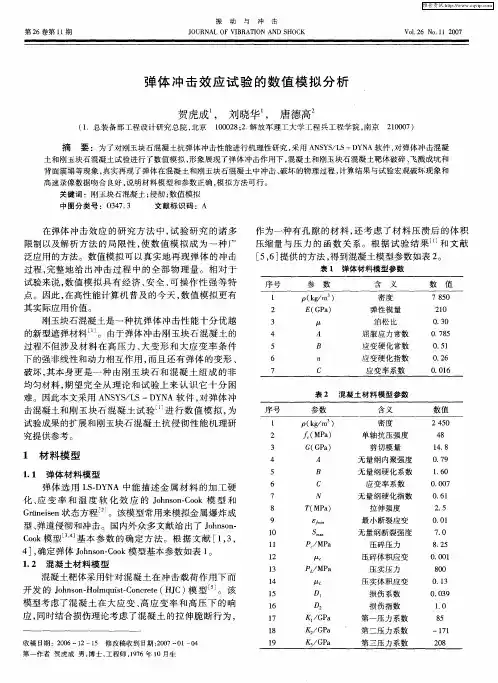
高速弹体冲击侵彻混凝土靶数值模拟分析摘 要: 采用有限元程序LS-DYNA 对高速弹体侵彻混凝土靶进行了数值仿真研究,根据Hamilton 原理和有限元理论建立了由弹塑性动力学控制方程。
结果表明:接触冲击算法能较为真实反映高速弹体对混凝土靶的侵彻过程;不同速度及弹头长径比不同的弹体对混凝土靶的侵彻深度有较大影响;通过与经验公式的验算结果对比进行误差分析,证明数值分析所得结果可靠。
基于HJC 材料模型的损伤分析可以提取出靶体单元的损伤情况。
研究结果对我国高速弹体对混凝土靶体的侵彻设计具有重要参考价值。
关键词:哈密尔顿原理;动力学控制方程;侵彻;经验公式;损伤Numerical simulation of High-velocity projectilepenetrating concrete targetsAbstract:LS-DYNA finite element software was applied to simulate the concrete target penetrated by High-velocity rigid projectile ,According to Hamilton principle and finite element theory, the dynamical governing equation of non-conservative system consist of elastic-plastic material was built. The result show that: the process of High-velocity projectile penetrating concrete targets can be well demonstrated by the contact impact algorithm . The velocity and the Hr/d ratio of projectile significant effect penetrating depth ;there were a contrast between the results from the formulas and the result from Numerical simulation , prove the Numerical simulation are reliable .based on the Johnson-Holmquist-concrete constitutive relations and damage model ,concrete element damage can obtained. The simulation result provide some reference for the design of projectiles and targets.Key words :Hamilton principle ; dynamical governing equation ; penetration ;emprical formula ;damage1 引言高速弹体在军事上有着广泛的应用,它能够钻入地下,贯穿防护工事,进入目标内部发生爆炸。
弹体侵彻靶体的过载特性及侵彻深度关系到提高侵彻武器打击性能的研究和防护材料,防护结构的优化设计。
侵彻问题属于高速冲击动力学的研究范畴,是高应变率,大变形,非线性碰撞现象,其过程具有高速,高温,高压等基本特征。
进行侵彻的原型实验需要耗费大量的人力,物力,财力。
数值模拟因其经济性和高效性日益成为侵彻问题的重要研究手段。
本文采用大型非线性LS-DYNA 有限元程序,建立三维模型动态模拟了高速弹体侵彻混凝土靶体的侵彻过程。
模拟结果可为侵彻武器设计者和防护工事设计者提供很好的理论参考。
2 基于Hamilton 原理的弹塑性动力学控制方程动态有限元程序是以动力学控制方程为基础的。
本文将耗散能引入到Lagrange 函数中,根据Hamilton 原理推导出了考虑能量耗散的弹塑性体动力学控制方程的有限元格式。
首先取一单元体,设单元体的动能为T ,应变能为U ,外力势能为W e ,对于保守系统,Lagrange 函数可取为:e W U T L --= (1)对于弹塑性介质的非保守系统,设塑性耗散功为W d ,建立拉格朗日函数为d e L T U W W =--- (2)设u 为单元体中任一点的位移矢量,eu 为单元体上各节点的位移矢量,它是时间t 的函数。
令单元体中任一点的位移矢量u 用单元体上各节点的位移矢量eu 表示为:e Nu u = (3)式中N 为形函数矩阵,它是坐标z y x ,,的函数。
e u N u= (4) 于是可求得单元体的动能为()dV u N N u dV u u T eT T e vT v ρρ⎰⎰⎰⎰⎰⎰==2121 (5) 式中ρ为单元体积的质量。
按照几何关系,应变与节点位移之间的关系为e Bu =ε (6)式中B 为应变位移矩阵,它是几何矩阵,与时间t 无关。
则应变率与节点速率的关系为e Bu ε= (7) 对于弹塑性介质单元体的应变能为vU UdV =⎰⎰⎰ (8)式中:U 表示单位体积的应变能实际结构均存在着阻尼,计算结构在动载荷作用下的动态响应时,阻尼对结构动态响应的幅值和相位都有很大影响,正确的描述结构的阻尼对结构的动态响应分析至关重要。
结构的阻尼耗散可分为2个部分,(1)与质点的运动速度有关的耗散,其耗散力与质点的运动速度成正比,(2)与应变率有关的耗散对于阻尼耗散的第一部分,设单元体振动时,阻尼系数为c ,则单元体积上所受的阻尼力v f 为uc f v -= (9) 对于阻尼耗散的第二部分,与应变率有关的广义阻尼力r f 为εβ D f r = (10) 则单元体上阻尼力所消耗的能量为()()dV Nu N u c udV u c W eT T e vT v v ⎰⎰⎰⎰⎰⎰-=-=2121 (11)()dV u DB B u dV D W e VT T e V T r ⎰⎰⎰⎰⎰⎰-=-=βεβε2121 (12) 单元体上所受的外力分为两部分,即体积力),,(z y x V F F F F =和表面力),,(z y x S F F F F =。
它们的势能分别为21,e e W W 。
()dV F N u dV F u W V T TVe vV T e ⎰⎰⎰⎰⎰⎰-=-=1 (13)()dS F N u dS F u W SS T Te SS T e ⎰⎰⎰⎰-=-=2 (14)于是拉格朗日函数为()()()()12()T T T e T e e T e e T e vTe T T e T V S vSL u N Nu U c u N Nu u B DBu dV u N F dV uN F dSρβ⎡⎤=-++⎢⎥⎣⎦++⎰⎰⎰⎰⎰⎰⎰⎰ (15)由哈密尔顿原理[1-3],将其在时间(t 1,t 2)上对L 积分,并使其变分等于0。
02121==⎰⎰t t t t Ldt Ldt δδ (16)Lagrange 函数中各项的变分可表达如下:()dV u N N uT ve T Te ⎰⎰⎰= ρδδ (17) T vvU UdV dV δδδεσ==⎰⎰⎰⎰⎰⎰ (18)()()()() =Te Te p v TTe Te e Te e p vvU uB D dV uBD Bu dV uBD dVδδεεδδε⎛⎫=- ⎪⎝⎭-⎰⎰⎰⎰⎰⎰⎰⎰⎰ (19)()dV Nu cN u W e T Tve v ⎰⎰⎰-= δδ (20) ()dV Bu D B uW e e T Tve r βδδ⎰⎰⎰-= (21) ()1Te T e V VW u N F dV δδ⎛⎫=- ⎪⎝⎭⎰⎰⎰ (22)()2Te Te S S W uN F dS δδ⎛⎫=- ⎪⎝⎭⎰⎰ (23)将表达式(17)~(23)代入表达式(16)采用分部积分,并有()01=t u e δ,()02=t u e δ可得()()()()()()()0][2121=⎪⎪⎭⎫ ⎝⎛+⎪⎪⎭⎫ ⎝⎛+-⎪⎪⎭⎫ ⎝⎛-⎪⎪⎭⎫ ⎝⎛+⎪⎪⎭⎫⎝⎛-⎪⎪⎭⎫ ⎝⎛-=⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰dt dS F N u dV F N u dV u B D B u u dV N cN u u BdV D B u u BdV D B u u dV N N u Ldt S S T T e V V T T e ee T T v e e v T T e e v p T T e ev e T Te t t e vT Te t t δδβδδδδρδδ (24) 令,,,,eq eq eq eq p K M C F F 分别表示单元体的刚度矩阵,质量矩阵,阻尼矩阵,外载荷矩阵和由塑性变形产生的广义荷载矩阵则有T eq e vT p e p vT eq vT T eq e vvT T eq V s vSK B D BdVF B D dVM N NdVC cN NdV BD BdVF N F dV N F dSερβ====+=+⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰ (25)由此得到()[]02121=++---=⎰⎰t t eq p e eq e eq e eq Te t t dt F F u C u K uM u Ldt δδ (26) 因为积分区间任意,所以被积函数()[]0=++---eq p e eq e eq e eq Te F F u C u K uM u δ (27) 由于单元体的变分()Teu δ任意,所以0=++---eq p e eq e eq e eq F F u C u K uM (28) 即e e e eq eq eq eq p M uC u K u F F ++=+ (29) 将式(29)写为增量形式的动力学控制方程:e e e eq eq eq eq p M uC u K u F F ∆+∆+∆=∆+∆ (30) 式(30)中,eq F ∆和p F ∆分别表示外载荷矩阵增量和由塑性变形产生的广义荷载矩阵增量,其表达式为:T p e p vF B D dV ε∆=∆⎰⎰⎰T T eq V s vSF N F dV N F dS ∆=∆+∆⎰⎰⎰⎰⎰动态有限元程序,是通过逐步时间积分来求解动力学方程的,需要选定合适的加载时间步长控制解法的稳定性,加载时间步长Δt 选得过小,将增加计算时间,加载时间步长Δt 选得过大将影响计算精度,对于冲击动态载荷,本文参考文献[4]中的公式确定时间步长为18lt λ∆∆≤(31) 式中:Δl 为结构中最小单元的特征尺寸,λ为纵波波速。