七年级下册数学知识竞赛

2022-2023学年度下学期七年级第一次知识竞赛数学试题学校:___________姓名：___________班级：___________考号：___________第I 卷（选择题）一、单选题(共64分)1．下列万程中，是二元一次方程组的是（ ）①2327x y y z -=⎧⎨+=⎩ ①1421y x y x ⎧+=⎪⎪⎨⎪-=-⎪⎩①()34215x x x y ⎧--=⎨-=⎩ ①1231232x y x y ⎧-=⎪⎪⎨⎪+=⎪⎩ A ．①①① B ．①① C ．①① D ．①①2．小亮求得方程组2212x y x y ●+=⎧⎨-=⎩的解为5x y =⎧⎨=⎩★，由于不小心，滴上了两滴墨水，刚好遮住了两个数●和①，请你帮他找回这两个数，“●”“①”表示的数分别为（ ）A ．5，2B ．5，2-C ．8，2D ．8，2-3．如图，下列条件中：①①1=①3；①①4=①5；①①2+①4=180°；①①2=①6，其中不能判断直线1l //2l 的是（ ）A ．①①①B ．①①C ．①D ．①4．某地突发地震，为了紧急安置40名地震灾民，需要搭建可容纳6人或4人的帐篷，若所搭建的帐篷恰好(既不多也不少)能容纳这40名灾民，则不同的搭建方案有（ ） A ．2种 B ．3种 C ．4种D ．6种5．下列判断中，正确的是（ ）A ．方程x y =不是二元一次方程B ．任何一个二元一次方程都只有一个解C ．方程25x y -=有无数个解，任何一对x 、y 都是该方程的解D ．21x y =⎧⎨=-⎩既是方程24x y -=的解也是方程231x y +=的解 6．已知21x y =⎧⎨=⎩是二元一次方程组91mx ny nx my +=⎧⎨-=⎩的解，则3m n -的值为（ ） A ．8 B ．5 C ．3 D ．107．由方程组 可得出x 与y 的关系式是（ ）A ．x+y=9B ．x+y=3C ．x+y=－3D ．x+y=－98．以一个二元一次方程组中的两个方程作为一次函数画图象，所得的两条直线（ ） A ．有一个交点 B ．有无数个交点 C ．没有交点 D ．以上都有可能 9．天虹商场现销售某品牌运动套装，上衣和裤子一套售价500元，若将上衣价格下调5%，将裤子价格上调8%，则这样一套运动套装的售价提高0.2%，设上衣和裤子在调价前单价分别为x 元和y 元，则可列方程组为（ ）A ．500(15%)(18%)500(10.2%)x y x y +=⎧⎨++-=⨯+⎩B ．500(15%)(18%)5000.2%x y x y +=⎧⎨-+-=⨯⎩C ．500(15%)(18%)500(10.2%)x y x y +=⎧⎨-++=⨯+⎩D ．5005%8%500(10.2%)x y x y +=⎧⎨+=⨯+⎩ 10．某校开展社团活动，参加活动的同学要分组活动，若每组7人，则余3人；若每组8人，则少5人；求课外活动小组的人数x 和分成的组数y ，可列方程组为( )A ．7385y x y x =-⎧⎨=+⎩B ．7385y x y x =+⎧⎨+=⎩C ．7385x y x y +=⎧⎨-=⎩D ．73 85y x y x =+⎧⎨=+⎩11．A ，B 两地相距100 km ，甲、乙两人骑车同时分别从A ，B 两地相向而行．假设他们都保持匀速行驶，则他们各自到A 地的距离()km s 都是骑车时间()h t 的一次函数，其图像如图所示．已知1 h 后乙距离A 地80 km ，2 h 后甲距离A 地30 km ，则经过多长时间两人将相遇？（ ）A ．3 hB ．20h 7C ．7h 2D ．4 h 12．如图，一次函数y =kx +b 与正比例函数y =2x 的图象交于点A ，则关于x ，y 的方程组2y kx b y x =+⎧⎨=⎩的解为( )A ．21x y =⎧⎨=-⎩B ．12x y =⎧⎨=⎩C ．21x y =⎧⎨=⎩D ．13x y =-⎧⎨=⎩13．某车间有60名工人生产太阳镜，1名工人每天可生产镜片200片或镜架50个．应如何分配工人生产镜片和镜架，才能使产品配套？设安排x 名工人生产镜片，y 名工人生产镜架，则可列方程组（ ）A ．60200250x y x y +=⎧⎨=⨯⎩B ．6020050x y x y +=⎧⎨=⎩C ．6050200x y x y +=⎧⎨=⎩D ．60220050x y x y +=⎧⎨⨯=⎩14．甲是乙现在的年龄时，乙10岁，乙是甲现在的年龄时，甲25岁，那么（ ） A ．甲比乙大5岁 B ．甲比乙大10岁 C ．乙比甲大10岁 D ．乙比甲大5岁 15．在同一平面直角坐标系中，一次函数y ax b =+与()0y mx n a m =+<<的图象如图所示，小星根据图象得到如下结论：①在一次函数y mx n =+的图象中，y 的值随着x 值的增大而增大；①方程组y ax b y mx n-=⎧⎨-=⎩的解为32x y =-⎧⎨=⎩； ①方程0mx n +=的解为2x =；①当0x =时，1ax b +=-．其中结论正确的个数是（ ） A ．1 B ．2 C ．3 D ．416．在平面直角坐标系中，点P （x ，y ）的坐标x ，y 满足二元一次方程21x y -=-，则称点P 为“智慧点”．例如：点A （1，3）满足213=1⨯--，所以点A 为“智慧点”．如图，在平面直角坐标系中，点 1A ，2A ，3A ，…均在格点上，其按图中“−−→”方向排列，如1A （0，0），201A （，），311A （，），410A （，）…，则依图中所示规律，1A ，2A ，3A ，…，2022A 这些点中，“智慧点”的总数为（ ）A ．503个B ．504个C ．505个D ．506个第II 卷（非选择题）二、填空题(共24分)17．如图，C 岛在A 岛的北偏东50︒方向，C 岛在B 岛的北偏西35︒方向，则ACB ∠的大小是____________．18．若方程()()2293210m x m x y ---++=是关于x y ，的二元一次方程，则m 的值为______．19．光线从空气射入水中时，光线的传播方向会发生改变，这就是折射现象．如图，水面MN 与底面EF 平行，光线AB 从空气射入水里时发生了折射，变成光线BC 射到水底C 处射线X BD 是光线AB 的延长线，160∠=︒，243∠=︒，则DBC ∠的度数为___________． 20．小颖家离学校1200米，其中有一段为上坡路，另一段为下坡路．她去学校共用了16分钟．假设小颖上坡路的平均速度是3千米/时，下坡路的平均速度是5千米/时．若设小颖上坡用了x 分钟，下坡用了y 分钟，根据题意可列方程组为_____________．21．小慧去花店买鲜花，若买6支玫瑰和4支百合，则她所带的钱还剩11元；若买4支玫瑰和6支百合，则她所带的钱还缺5元．若她想购买10支百合，则她所带的钱还缺______元．22．若关于x ，y 的方程组111222a xb yc a x b y c +=⎧⎨+=⎩的解为32x y =⎧⎨=⎩，则方程组11122252605260a x b y c a x b y c +-=⎧⎨+-=⎩的解为__________．三、解答题(共92分)23．（共10分）用适当的方法解下列方程组：(1)2127y x x y =-⎧⎨+=-⎩． （5分） (2)11233210x y x y +⎧-=⎪⎨⎪+=⎩．（5分）24．（8分）阅读下面情境：甲、乙两人共同解方程组51542ax y x by +=⎧⎨-=-⎩①②，由于甲看错了方程①中的a ，得到方程组的解为31x y =-⎧⎨=-⎩；乙看错了方程①中的b ，得到方程组的解为54x y =⎧⎨=⎩．试求出a 、b 的值，并计算20222021110a b ⎛⎫+- ⎪⎝⎭的值．25．（8分）有一个两位数，它的十位上的数字比个位上的数字小2，十位上的数字与个位上的数字之和的4倍刚好等于这个两位数．求这个两位数．26．（10分）已知关于x ，y 的方程组53212x y m x y m +=-⎧⎨-=-+⎩的解中x 与y 的和为3，求m 的值及此方程组的解．27．（12分）初中生涯即将结束，同学们为友谊长存，决定互送礼物，于是去某礼品店购进了一批适合学生的毕业纪念品．已知购进3个A 种礼品和2个B 种礼品共54需元，购进2个A 种礼品和3个B 种礼品共需46元．(1)A ，B 两种礼品每个的进价是多少元？（6分）(2)该店进货时，A 种礼品不少于60个，已知A 种礼品每个售价为20元，B 种礼品每个售价为9元，若该店全部售完获利为W 元，试说明如何进货获利最大？最大为多少元？（6分）28．（14分）已知关于x ，y 的方程组37x y ax b y -=⎧⎨+=⎩和28x by a x y +=⎧⎨+=⎩的解相同． (1)求a ，b 的值；（6分）(2)若直线11:l y ax =+与直线21:2l y x b =-+分别交y 轴于点A 、B ，两直线交于点P ，求ABP 的面积．（8分）。

七年级数学竞赛试题及答案一、选择题1. 下列哪个分数是最简分数？A. 2/4B. 3/6C. 5/10D. 3/52. 计算：(2x + 3)(x - 2) = ?A. 2x^2 - x - 6B. 2x^2 - 4x + 3x - 6C. 2x^2 - 6x + 3D. 2x^2 - 2x - 63. 一个长方形的长是12cm，宽是8cm，那么它的面积是多少平方厘米？A. 20B. 96C. 120D. 2004. 一个等差数列的前三项分别是2，5，8，那么第10项是多少？A. 20B. 22C. 24D. 265. 一个圆的半径是7cm，求这个圆的周长（π取3.14）。

A. 14cmB. 28cmC. 42cmD. 56cm二、填空题1. 一个等边三角形的每个内角是______度。

2. 如果a:b = 3:4，那么b:a = ______3. 一个分数的分子是12，分母是18，这个分数化简后的结果是______。

4. 一个长方体的体积是60立方厘米，长是5cm，宽是2cm，那么它的高是______厘米。

5. 一个圆的直径是10cm，求这个圆的面积（π取3.14）。

三、解答题1. 甲乙两人同时从A地出发，甲以每小时5公里的速度向东走，乙以每小时7公里的速度向南走。

如果他们各自沿着直线走到B地和C地，且B、C两地相距10公里，求甲乙两人出发后多少时间相遇。

2. 一个班级有40名学生，其中男生和女生的比例是3:2。

如果增加10名女生，那么男生和女生的比例将变为多少？3. 一个数除以4余1，除以5余2，除以6余3，这个数最小是多少？4. 一块长方形的草坪长是20米，宽是15米。

现在要在草坪的四周种上一圈花，每株花占地0.2平方米，问需要多少株花？5. 一个数的平方减去它的三倍再加上20得到的结果是5，求这个数是多少？四、证明题1. 证明：勾股定理。

在一个直角三角形中，直角边的平方和等于斜边的平方。

2. 证明：两个等边三角形如果它们的边长相等，那么这两个三角形全等。

初一下数学竞赛试题及答案【试题一】题目：一个数的平方根是另一个数的立方根，求这个数。

【答案】设这个数为 \( x \)，则根据题意，我们有 \( \sqrt{x} =\sqrt[3]{y} \)，其中 \( y \) 是另一个数。

将等式两边立方，得到\( x = y^{1/3} \)。

由于 \( y \) 可以是任意数，\( x \) 也可以是任意数的立方。

例如，如果 \( y = 8 \)，则 \( x = 2 \)。

【试题二】题目：一个直角三角形的两条直角边分别为 \( 3 \) 厘米和 \( 4 \) 厘米，求斜边的长度。

【答案】根据勾股定理，直角三角形的斜边长度 \( c \) 可以通过公式 \( c = \sqrt{a^2 + b^2} \) 计算，其中 \( a \) 和 \( b \) 是直角边的长度。

将 \( a = 3 \) 和 \( b = 4 \) 代入公式，得到 \( c = \sqrt{3^2 + 4^2} = \sqrt{9 + 16} = \sqrt{25} = 5 \) 厘米。

【试题三】题目：如果一个数的 5 倍加上 12 等于这个数的 3 倍减去 8，求这个数。

【答案】设这个数为 \( x \)，根据题意，我们有 \( 5x + 12 = 3x - 8 \)。

将等式两边的 \( x \) 项移项，得到 \( 2x = -20 \)。

解得 \( x = -10 \)。

【试题四】题目：一个圆的半径是 7 厘米，求这个圆的面积。

【答案】圆的面积 \( A \) 可以通过公式 \( A = \pi r^2 \) 计算，其中\( r \) 是圆的半径。

将 \( r = 7 \) 代入公式，得到 \( A = \pi \times 7^2 = 49\pi \) 平方厘米。

【试题五】题目：一个分数的分子和分母的和是 21，且这个分数等于\( \frac{3}{4} \)，求这个分数。

人教版初一下数学竞赛试题及答案一、选择题（每题3分，共30分）1. 下列哪个数是最小的正整数？A. 0B. -1C. 1D. 22. 如果a和b是两个连续的整数，且a > b，那么a-b的值是：A. 1B. 0C. -1D. 23. 一个数的平方根是它本身，这个数可以是：A. 1B. -1C. 0D. 44. 一个数的立方等于它本身，这个数有：A. 1个B. 2个C. 3个D. 4个5. 一个圆的半径是r，它的面积是：A. πr²B. 2πrC. πrD. r²6. 一个长方体的长、宽、高分别是a、b、c，它的体积是：A. abcB. 2abcC. a+b+cD. a²b²c²7. 一个等差数列的首项是a，公差是d，第n项是：A. a+(n-1)dB. a+ndC. a-dD. a-d(n-1)8. 如果一个三角形的三边长分别为a、b、c，且a² + b² = c²，那么这个三角形是：A. 直角三角形B. 等边三角形C. 等腰三角形D. 不规则三角形9. 一个分数的分子和分母同时扩大相同的倍数，其值：A. 增大B. 减小C. 不变D. 无法确定10. 一个数的绝对值是它本身，这个数：A. 必须为正数B. 必须为负数C. 可以是正数或零D. 可以是负数或零二、填空题（每题4分，共20分）11. 一个数的平方等于16，这个数是________。

12. 如果一个数的相反数是-5，那么这个数是________。

13. 一个数的绝对值等于5，这个数可以是________。

14. 一个数的立方根是2，那么这个数是________。

15. 一个数的倒数是1/4，这个数是________。

三、解答题（每题10分，共50分）16. 计算下列表达式的值：(3+5)² - 2×(4-1)。

17. 一个长方体的长是10厘米，宽是8厘米，高是6厘米，求它的表面积和体积。

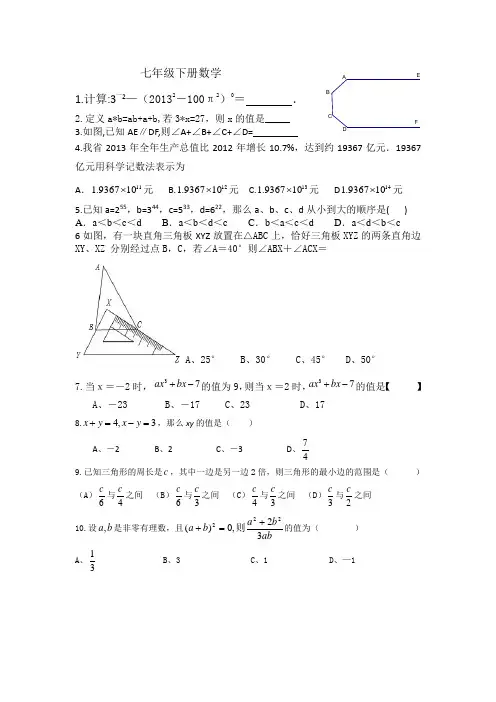
七年级下册数学1.计算:3—2—（20132－100π2）0＝ ．2.定义a*b=ab+a+b,若3*x=27，则x 的值是_____3.如图,已知AE ∥DF,则∠A+∠B+∠C+∠D=_________4.我省2013年全年生产总值比2012年增长10.7%，达到约19367亿元．19367亿元用科学记数法表示为A ．11109367.1⨯元 B.12109367.1⨯元 C.13109367.1⨯元 D 14109367.1⨯元55443322XY 、XZ 分别经过点B ，C ，若∠A ＝40°则∠ABX ＋∠ACX ＝A 、25°B 、30°C 、45°D 、50°7.当ｘ＝－2时， 37ax bx +-的值为9，则当ｘ＝2时，37ax bx +-的值是【 】A 、－23B 、－17C 、23D 、178.4,3x y x y +=-=，那么xy 的值是（ ）A 、－2B 、2C 、－3D 、749.已知三角形的周长是c ，其中一边是另一边2倍，则三角形的最小边的范围是（ ） （A ）6c 与4c 之间 （B ）6c 与3c 之间 （C ）4c 与3c 之间 （D ）3c 与2c之间 10.设b a ,是非零有理数，且abb a b a 32,0)(222+=+则的值为（ ）A 、31B 、3C 、1D 、—1 FEDCBA14.已知m m Q m P 158,11572-=-=（m 为任意实数），则P 、Q 的大小关系为（ ） A 、Q P > B 、Q P = C 、Q P < D 、不能确定16.设12142++mx x 是一个完全平方式，则m =______________20.计算2(123456789)123456788123456790-⨯=23.如果2005m -与()22006n -互为相反数，那么()2007m n -=24. 2005200640.25⨯= 24(21)(21)(21)+++=29.如上图，正方形ABCD 的边长为1，点M 、N 分别为BC 、CD 上的动点， 且满足△CMN 的周长为2，则∠MAN ＝_______度. 30如图，直线l 1∥l 2，AB ⊥l 1，垂足为O ，BC 与l 2相 交与点E ，若∠1=43°则∠2= 度.31.已知三角形的两边长分别为7和2，第三边的数值是奇数，则第三边长是_ __. 32.设n 是一个非零自然数，那么一定存在自然数m ，能使mn ＋1是完全平方数，这样的自然数对（m ，n ）很多，请写出两对.35.时钟在12点25分时，分针与时针之间的夹角度数为36.已知一个三角形三边是不相等的整数，且周长小于13，这样的三角形有个38.已知x+x 1- 6=0, (1)求x 2+21x的值。

卜人入州八九几市潮王学校长郡教育集团二零二零—二零二壹七年级数学下学期知识竞赛试题一、填空题〔每一小题4分，一共40分〕 1、a 、b 互为相反数，c 、d 互为倒数，那么()=-+cdb a 351_______________； 2、假设71-=x ，那么x =；3、假设A 22223,3y xy xB y xy x +-=++=，那么A —[B+2B —(A+B)]化简后的结果为_________〔用含x 、y 的代数式表示〕 4、设多项式M d cx bx ax=+++35，当x ＝0时，5-=M ；当3-=x 时，7=M ，那么当3=x 时，M＝；5、一队卡车运一批货物，假设每辆车装7吨货物，那么尚余10吨货物装不完；假设每辆车装8吨货物，那么最后一辆车只装3吨货物就装完了这批货物，那么这批货物一共有______________吨；6、方程组的解为；7、关于x 的不等式组0321x a x -≥⎧⎨-≥-⎩的整数解一共有5个，那么a 的取值范围是________8、如图：在△ABC 中，AB=5，AC=9，那么BC 边上的中线AD 的长的取值范围是______；9、如图，在△ABC 中，AB=AC ，∠BAD ＝30°， 且AE=AD ，那么∠EDC 的度数是10、组织同学们看电影，排队在街上匀速行走， 有位同学注意到从背后每隔4分钟过一辆公一共汽车， 而迎面每隔12分钟有一辆公一共汽车驶过，车站 发车的时间是间隔是一样的，那么车站每隔分钟发一辆车； 二、选择题〔每一小题3分，一共30分〕 11、数：2003(1)--是〔〕.〔A 〕最大的负整数〔B 〕绝对值最小的整数〔C 〕最小的正整数〔D 〕最大的负数12、假设为有理数，且，那么〔〕第9题图ABC D第8题图BCEDA〔A 〕－8 〔B 〕－16 〔C 〕8 〔D 〕1613、由1，2，3，4这四个数字组成四位数abcd 〔数字可重复使用〕，要求满足a c b d +=+.这样的四位数一共有〔〕〔A 〕36个〔B 〕40个〔C 〕44个(D)48个.14、假设方程组3133x y k x y +=+⎧⎨+=⎩的解为x,y ，且2<k <4，那么x-y 的取值范围是〔〕〔A 〕0<x-y <0.5〔B 〕0<x-y <1〔C 〕-3<x-y <-1〔D 〕-1<x-y <1 15、如图，AB ∥ED ，∠C ＝o90，∠ABC ＝∠DEF ，∠D ＝o130， ∠F ＝o100，那么∠E 的度数为〔〕 (A)160°〔B 〕150°〔C 〕145°〔D 〕140° 16、黑板上写有111123100，　， ，，　一共100个数字．每次操作先从黑板上的数中选取2个数a b ，，然后擦去a b ，，并在黑板上写上数a b ab ++，那么经过99次操作后，黑板上剩下的数是〔〕． 〔A 〕2021〔B 〕101〔C 〕100〔D 〕9917、在古代生活中，有很多时候也要用到不少的数学知识，比方有这样一道题： “隔墙听得客分银，不知人数不知银.七两分之多四两，九两分之少半斤〞〔注：古秤十六两为一斤〕 请同学们想想有几人，几两银？〔〕. 〔A 〕六人，四十四两银〔B 〕五人，三十九两银 〔C 〕六人，四十六两银〔D 〕以上都不对18、王老伯在集上先买回5只羊，平均每只a 元，稍后又买回3只羊，平均每只b 元，后 来他以每只2ba +的价格把羊全部卖掉了，结果发现赔了钱，赔钱的原因是〔〕 〔A 〕b a>〔B 〕b a <〔C 〕b a =〔D 〕与a 、b 的大小无关19、如图，正方形ABCD 的面积为90．点P 在AB 上，；X ，Y ，Z 三点在BD 上，且，那么△PZX 的面积为()A BCDEF20、正三角形ABC所在平面内有一点P，使得△PAB、△PBC、△PCA都是等腰三角形，那么这样的P点有〔〕〔A〕1个〔B〕4个〔C〕7个〔D〕10个三、解答题〔第21题6分，第22至23题每一小题7分，第24题10分，一共30分〕22、由于电力紧张，某地决定对工厂实行“峰谷〞用电．规定：在每天的8:00至22:00为“峰电〞期,电价为a元/度；每天22:00至8:00为为“谷电〞期,电价为b元/度．下表为某厂4、5月份的用电量和电费的情况统计表：月份用电量〔万度〕电费〔万元〕4 125 16〔1〕假设4月份“谷电〞的用电量占当月总电量的13，5月份“谷电〞的用电量占当月总用电量的41，求a、b的值．〔2〕假设6月份该厂预计用电20万度，为将电费控制在10万元至万元之间〔不含10万元和万元〕，那么该厂6月份在“谷电〞的用电量占当月用电量的比例应在什么范围？23、光华农机租赁公司一共有50台结合收割机，其中甲型20台，乙型30台.现将这50台结合收割机派往A、B两地区收割小麦，其中30台派往A地区，20台派往B地区.两地区与该农机租赁公司商定的每天的租赁价格见下表：每台甲型收割机的租金每台乙型收割机的租金A地区1800元1600元B地区1600元1200元〔1〕设派往A地区x台乙型结合收割机，租赁公司这50台结合收割机一天获得的租金为y(元)，用含x的代数式表示y〔即写出y与x之间的数量关系式〕，并写出x的取值范围；〔2〕假设使农机租赁公司这50台结合收割机一天获得的租金总额不低于79600元，说明有多少种分派方案，并将各种方案设计出来；21、FMD ABCN 〔3〕假设要使这50台结合收割机每天获得的租金最高，请你为光华农机租赁公司选择分派方案。

数学竞赛试题初一及答案一、选择题（每题3分，共30分）1. 下列哪个数是最小的正整数？A. 0B. 1C. -1D. 2答案：B2. 计算下列哪个选项的结果等于10？A. 3 + 7B. 4 × 2C. 5 - 3D. 6 ÷ 2答案：A3. 如果一个数的平方等于9，那么这个数是：A. 3B. -3C. 3或-3D. 以上都不是答案：C4. 一个长方形的长是10厘米，宽是5厘米，那么它的面积是多少平方厘米？A. 20B. 30C. 50D. 60答案：C5. 一个数加上它的相反数等于：A. 0B. 1C. 2D. 无法确定答案：A6. 下列哪个分数是最简分数？A. 6/8B. 9/12C. 5/10D. 7/14答案：D7. 一个圆的直径是14厘米，那么它的半径是多少厘米？A. 7B. 14C. 28D. 无法确定答案：A8. 如果一个三角形的两个内角分别是40度和60度，那么第三个内角是多少度？A. 40B. 60C. 80D. 无法确定答案：C9. 一个数的立方等于8，那么这个数是：A. 2B. -2C. 2或-2D. 以上都不是答案：A10. 一个数的绝对值是5，那么这个数可能是：A. 5B. -5C. 5或-5D. 以上都不是答案：C二、填空题（每题4分，共20分）11. 一个数的平方根是4，那么这个数是______。

答案：1612. 如果一个数的一半是10，那么这个数是______。

答案：2013. 一个数的倒数是2，那么这个数是______。

答案：1/214. 一个数的立方等于27，那么这个数是______。

答案：315. 一个数的绝对值是3，那么这个数可能是______或______。

答案：3或-3三、解答题（每题10分，共50分）16. 计算下列表达式的值：(3x - 2) + (4x + 5)，其中x = 2。

答案：首先将x的值代入表达式，得到(3×2 - 2) + (4×2 + 5) = 6 + 8 + 5 = 19。

七年级下数学竞赛试题一、选择题（每题3分，共15分）1. 如果一个数的平方等于它本身，那么这个数可能是：A. 0B. 1C. -1D. 所有选项2. 下列哪个代数式不能表示为两个数的平方和：A. 5B. 6C. 7D. 83. 一个直角三角形的两条直角边分别为3和4，那么它的斜边长度是：A. 5B. 6C. 7D. 84. 一个数列的前三项是1, 1, 2，从第四项开始，每一项都是前三项的和。

这个数列的第10项是：A. 144B. 89C. 233D. 14405. 一个圆的半径是5，那么它的面积是：A. 25πB. 50πC. 75πD. 100π二、填空题（每题2分，共10分）6. 如果一个数的立方等于它本身，那么这个数是______。

7. 一个数的绝对值是它本身，这个数是______或______。

8. 一个数的相反数是它本身，这个数是______。

9. 如果一个数的平方根是2，那么这个数是______。

10. 一个数的立方根是3，那么这个数是______。

三、解答题（每题5分，共20分）11. 证明勾股定理：在一个直角三角形中，斜边的平方等于两直角边的平方和。

12. 解方程：\( x^2 - 5x + 6 = 0 \)。

13. 证明：如果一个数的平方和它的立方相等，那么这个数只能是0或1。

14. 计算：\( \sqrt{81} + \frac{1}{2} - \frac{2}{3} \)。

四、应用题（每题10分，共20分）15. 一个农场主有一块长为20米，宽为10米的矩形土地。

他想在这块土地上种植果树，每棵果树需要2平方米的空间。

请问他最多可以种植多少棵果树？16. 一个班级有40名学生，其中1/3的学生参加了数学竞赛，1/4的学生参加了科学竞赛。

如果参加数学竞赛的学生中有一半也参加了科学竞赛，那么至少有多少名学生参加了至少一项竞赛？五、开放性问题（每题15分，共30分）17. 假设你有一个无限长的直尺和一个圆规，你能用它们来构造一个正十七边形吗？如果可以，请描述你的构造方法。

初一数学下竞赛试题及答案一、选择题（每题3分，共30分）1. 若a和b互为相反数，且a+b=0，那么a的值是多少？A. 0B. 1C. -1D. 无法确定2. 下列哪个数是质数？A. 8B. 9C. 10D. 113. 一个数的平方根是4，这个数是多少？A. 16B. 8C. 4D. 24. 一个长方体的长、宽、高分别是a、b、c，它的体积是多少？A. abcB. a + b + cC. a - b - cD. a/b + c5. 一个圆的半径是5，它的周长是多少？A. 10πC. 25πD. 30π6. 一个数的绝对值是5，这个数可能是？A. 5B. -5C. 5或-5D. 都不是7. 如果x=2y，那么2x=？A. 2yB. 3yC. 4yD. 5y8. 一个直角三角形的两条直角边分别是3和4，斜边是多少？A. 5B. 6C. 7D. 89. 一个数的立方是-27，这个数是多少？A. 3B. -3C. 9D. -910. 一个数的倒数是1/4，这个数是多少？A. 4B. 1/4D. 1二、填空题（每题2分，共20分）11. 一个数的平方是25，这个数是________。

12. 一个数的立方是64，这个数是________。

13. 一个数的绝对值是10，这个数是________。

14. 如果一个数的相反数是-7，那么这个数是________。

15. 一个数的平方根是2或-2，这个数是________。

16. 一个数的倒数是3，这个数是________。

17. 如果x=3y，那么3x=________。

18. 一个直角三角形的两条直角边分别是5和12，斜边是________。

19. 一个圆的半径是10，它的周长是________。

20. 一个数的立方根是2，这个数是________。

三、解答题（每题10分，共50分）21. 证明勾股定理。

22. 解方程：x + 2 = 5。

23. 计算一个长方体的表面积，如果长方体的长、宽、高分别是2m、3m、4m。

2023~2023年七年级下学期数学竞赛试题一.选择题(每小题5分,共30分)1.若a<0 , ab<0 , 那么51---+-baab等于( )A . 4B .-4C . -2a+2b+6 D. 19962.数轴上坐标是整数的点称为整点,某数轴的单位长度是1厘米,若在这个数轴上随意画出一条长为2023厘米的线段AB,则线段AB盖住的整点的个数是( )A.2023 或2023 B . 2023或2023 C . 2023 或2023 D . 2023 或20233.已知{a x b y==是方程组{5272=+=+y x y x的解, 则a-b的值为( )A . 2B . 1 C. 0 D. -14.若a<3 , 则不等式(a-3)x<a-3的解集是( )A. x>1 B .x<1 C . x>-1 D . x<-15.方程2x+y=7的正整数解有( )A.一组 B .二组 C .三组 D . 四组6.不等式组{5335+<-<xxax的解集为x<4, 则a满足的条件是( )A. a<4 B .a=4 C .a≤4 D .a≥4二.填空题(每小题4分,共24分)1.不等式组{4252>+<-axbx的解集是0<x<2, 则a+b的值等于_______2.已知543zyx ==, 且10254=+-z y x ,则z y x +-52的值等于________3.计算200920081431321211⨯+⋅⋅⋅+⨯+⨯+⨯ = _________4.一个角的补角的31等于它的余角, 则这个角等于_____度.5.计算（1+715131++）×-91715131⎪⎪⎭⎫ ⎝⎛+++（1+91715131+++）×（715131++）=．6。

b b a -=+22若，______622=+-+b a b a 则三. 解答题:(,共46分). 1（本题6分）解方程组 345238x y x y -=⎧⎨+=-⎩，．2.（本题10分）已知: 0634=--z y x ，072=-+z y x ()0≠xyz ， 求代数式222222103225z y x z y x ---+的值3（本题10分）.如图,已知CD ⊥AB ，DE ∥BC,∠1=∠2求证:FG ⊥AB21G F E D CB A4．（本题10分）在平面直角坐标系中，已知三点()()()b c C b B a A ,,0,,,0，其中c b a ,,满足关系式()a b c b a -==-+-2,0322；（1）求c b a ,,的值,（2）请你将三点()()()b c C b B a A ,,0,,,0在平面直角坐标系中描出来，并计算出ABC ∆的面积。

七年级下册数学竞赛题和经典题含解答共10题1. 题目：甲、乙两个正整数的和是300，差是120，求甲、乙两个数分别是多少？解答：设甲的数为x，乙的数为y。

根据题意，我们可以得到以下两个方程：x + y = 300 （方程1）x - y = 120 （方程2）解方程组得到甲的数x = 210，乙的数y = 90。

2. 题目：某数的4倍减去该数的2倍等于30，求这个数。

解答：设这个数为x。

根据题意，我们可以得到以下方程：4x - 2x = 30化简得到2x = 30解方程得到x = 153. 题目：一个正整数加上自身的平方等于140，求这个正整数。

解答：设这个正整数为x。

根据题意，我们可以得到以下方程：x + x²= 140化简得到x²+ x - 140 = 0解方程得到x = 10 或x = -14，由题目要求为正整数，所以x = 10。

4. 题目：一个三位数加上它的逆序数等于1333，求这个三位数。

解答：设这个三位数为xyz。

根据题意，我们可以得到以下方程：100x + 10y + z + 100z + 10y + x = 1333化简得到101x + 20y + 101z = 1333由于101为质数，所以x和z只能为1，y只能为6。

解方程得到x = 1，y = 6，z = 1，所以这个三位数为161。

5. 题目：甲、乙两个数的和是90，差是20，求甲、乙两个数分别是多少？解答：设甲的数为x，乙的数为y。

根据题意，我们可以得到以下两个方程：x + y = 90 （方程1）x - y = 20 （方程2）解方程组得到甲的数x = 55，乙的数y = 35。

6. 题目：某个三位数的百位数是7，个位数是2，且各位上的数字之和是13，求这个三位数。

解答：设这个三位数为xyz。

根据题意，我们可以得到以下方程：x = 7 （百位数是7）z = 2 （个位数是2）x + y + z = 13 （各位上的数字之和是13）代入得到7 + y + 2 = 13解方程得到y = 4所以这个三位数为742。

七年级下册数学竞赛题1. 小明在一张纸上画了一个周长为24厘米的直角三角形，如图所示。

请问这个三角形的面积是多少平方厘米？2. 一年级学生自己制作五个0～9的数字卡片，每次从中抽出两个不同的数字，把它们组合成两位数，然后用随机数表把这个两位数放到一个十格点数表的一个格子里，如下图所示。

请问这个点数表里能填满的最大的整数是多少？3. 在坐标平面上，有一个顶点在原点的正方形和一个圆。

他们的四个交点是A、B、C、D四个点。

请问，一个已知的点E （-1，1）是否在这个图形内，如果在，它在哪个区域？4. 小华用一片正方形的铁皮和两个线性烟缸做成了一个三棱柱，如图所示。

请问这个三棱柱的表面积是多少平方厘米？5. 一家超市有三种口香糖，每种口香糖的售价分别为1元、2元和3元。

现在要购买10块口香糖，每次购买可以选择任意一种口香糖，但每种口香糖的购买数量不超过4块。

请问，有多少种不同的购买方案？6. 一家咖啡店推出了一种新品，每杯售价12元。

现在有一项优惠活动，每购买10杯，可以减免2元。

小明想买50杯这种新品，请问他最少要支付多少钱？7. 有一张边长为6个单位的正方形纸片，你可以把它折叠成一个立体图形。

请问，这个立体图形的表面积最小可能是多少平方单位？8. 在一个2×2×2的立方体中，有6个顶点。

现在我们选择其中的三个顶点连接成一个三角形，请问，有多少种不同的三角形？9. 一组正整数之积为1000，它们的和最小为多少？10. 如果a+b+c=3，a²+b²+c²=5，且a,b,c均为正实数，那么3abc的最大值是多少？。

七年级（下）数学基础知识竞赛试卷题号一 二 三 总分 1—13 14—23 24 25 26 27 28 29 30 31 得分一、填空题（每题2分，共26分） 1． 若5814=--m x m 是关于x 的一元一次方程，则m =______。

2、三角形中有两边长为5和8，第三边长为x ，则x 的取值范围是 。

3、根据“a 的2倍与－5的和是非负数”列出不等式是 。

4、不等式13-3x ＞0的正整数解是_____ _____。

5、不等式6x<11x 成立的条件是 。

6、写出你喜欢的两个轴对称图形： 。

7、一个多边形的外角和是内角和的15，则边数n 等于 。

8、若等腰三角形的一个角的大小等于30°，则这个等腰三角形的顶角的大小为 。

9、如图，△ABC 中，AB=10cm ，AC 的中垂线ED 交AC 于E ，交AB 于D ，若BC=6cm ，则△CDB 的周长是 cm 。

10、K 时,方程k x 332-=5(x-k)+1的解是非负数。

11、设a 表示两位数，b 表示三位数，如果把a 放在b 的左边组成一个五位数，用代数式表示为 。

12、某商品售价a 元，利润为成本的20%，若把利润提高到30%，售价应提高到____ ___元。

13、一个等腰三角形一腰上的高与另一腰的夹角为45°，则该三角形顶角的度数为 。

二、选择题（每题3分，共30分）14、下列说法正确的是 ( )A ．圆的直径是它的对称轴B ．角的平分线是它的对称轴C ．线段的垂直平分线是它的对称轴D ．长方形只有4条对称轴15、已知等腰三角形的一边长为3，另一边长为8，则它的周长为（ ）A 、14B 、 19C 、11D 、14或1916、方程■52+=-x y x 是二元一次方程，■是被弄污的x 的系数，请你推断■的值属于下列情况中的（ ）A.不可能是-1B. 不可能是-2C.不可能是1D. 不可能是2 17、如果|y x 2-|+)3(-+y x 2=0成立，那么xy =（ ）B. 2C.9 18、我市股市交易中心每买、卖一次需千分之七点五的各种费用，某投资者以每股10元的价格买入上海某股票1000股，当该股票涨到12元时全部卖出，该投资者实际盈利为( )A ．1835元B ．1925元C ．2000元D ．1910元19、由下列所给边长相同的正多边形的结合中，不能铺满地面的是（ ）A 、正三角形与正方形结合B 、正三角形与正六边形结合C 、正方形与正六边形结合D 、正三角形、正方形、正六边形三者结合20、不等式组⎩⎨⎧>-<+-m x x x 62的解集是4>x ，那么m 的取值范围是（ ） A ．4≥m B ．4=m C ．4<m D ．4≤m21、不等式组240,10x x -<⎧⎨+⎩≥的解集在数轴上表示正确的是（ ）A ．B ．C ．D ．22、已知方程组2342x y ax by -=⎧⎨+=⎩与3564x y bx ay -=⎧⎨+=-⎩有相同的解，则a 、b 的值为( )° ．° －1 ． ．． ° °第9题A ．21a b =-⎧⎨=⎩B ．12a b =⎧⎨=-⎩C ．12a b =⎧⎨=⎩D ．12a b =-⎧⎨=-⎩23、如图，在AB=AC 的△ABC 中，D 是BC 边上任意一点，DF ⊥AC 于F ，E 在AB 边上，使ED ⊥BC 于D ，∠AED=155°，则∠EDF 等于（ ）A 、65°B 、50°C 、70°D 、75°三、解答题（共64分）24、解下列方程（组）：（1）142312-+=-x x （4分） （2） ⎪⎩⎪⎨⎧=--+-=+2)(5)(432y x y x y x y x （7分）25、求不等式组2(1)41413x x x x +-<⎧⎪+⎨>-⎪⎩ 的自然数解。

七年级下册数学竞赛试题一、选择题（每题3分，共15分）1. 下列哪个数不是整数？A. -5B. 0C. 3.14D. 20232. 一个长方形的长是宽的两倍，如果宽是a米，那么长方形的面积是多少？A. a^2B. 2a^2C. 3a^2D. 4a^23. 如果一个数的平方根是5，那么这个数是多少？A. 25B. -25C. 5D. -54. 下列哪个分数不能化简？A. 4/8B. 5/10C. 6/9D. 7/145. 一个圆的半径是5厘米，那么它的周长是多少？A. 10π cmB. 20π cmC. 30π cmD. 40π cm二、填空题（每题2分，共10分）6. 如果一个数的立方是-27，那么这个数是______。

7. 一个数的相反数是-3，那么这个数是______。

8. 如果a和b互为倒数，那么ab等于______。

9. 一个直角三角形的两条直角边分别是3和4，那么斜边的长度是______。

10. 一个数的绝对值是5，那么这个数可以是______。

三、计算题（每题5分，共20分）11. 计算下列表达式的值：(3x - 2y)(3x + 2y)。

12. 解方程：2x + 5 = 17。

13. 计算：(-2)^3 + 5 * (-3) - 4。

14. 简化分数：\(\frac{8}{12}\)。

四、解答题（每题10分，共30分）15. 一个班级有40名学生，其中2/3的学生参加了数学竞赛。

问有多少学生参加了数学竞赛？16. 一个商店销售两种类型的自行车，A型自行车每辆售价为300元，B型自行车每辆售价为400元。

如果商店总共卖出了20辆自行车，总收入为7200元，问A型和B型自行车各卖了多少辆？17. 一个长方体的长、宽、高分别是10厘米、8厘米和6厘米。

求这个长方体的表面积和体积。

五、应用题（每题15分，共30分）18. 某工厂计划在一个月内生产一批零件，如果每天生产120个零件，那么30天可以完成生产任务。