第十一章几何光学

第十一章 几何光学通过复习后，应该:1.掌握单球面折射成像、共轴球面系统、薄透镜成像、薄透镜的组合、放大镜和显微镜;2.理解共轴球面系统的三对基点、眼的分辨本领和视力、近视眼、远视眼、散光眼的矫正;3.了解透镜像差、眼的结构和性质、色盲、检眼镜、光导纤维内窥镜。

11-1 一球形透明体置于空气中，能将无穷远处的近轴光线束会聚于第二个折射面的顶点上，求此透明体的折射率。

习题11-1附图（原11-2附图）解: 无穷远处的光线入射球形透明体，相当于物距u 为∞，经第一折射面折射，会聚于第二折射面的顶点，则v=2r（r 为球的半径），已知n 1 =1.0，设n 2 =n（即透明体的折射率），代入单球面折射成像公式，得rn r n 1.0-20.1=+∞ 解得n =2.0，即球形透明体的折射率。

11-2 在3m 深的水池底部有一小石块，人在上方垂直向下观察，此石块被观察者看到的深度是多少?（水的折射率n =1.33）习题11-2附图（原11-3附图）解: 这时水池面为一平面的折射面，相当于r 为∞，已知u =3m，n 1 =1.33，n 2 =1.0，观察者看到的是石块所成的像，设其像距为v ，应用单球面折射成像公式，得∞=+ 1.33-.010.1m 333.1v 解得v =-2.25m，这表明石块在水平面下2.25m 处成一虚像，即观察者看到的“深度”。

11-3 圆柱形玻璃棒（n =1.5）放于空气中，其一端是半径为2.0cm 的凸球面，在棒的轴线上离棒端8.0cm 处放一点物，求其成像位置。

如将此棒放在某液体中（n =1.6），点物离棒端仍为8.0cm，问像又在何处?是实像还是虚像?习题11-3附图 （a）【原11-5附图（a）】解: ①如本题附图（a）所示，已知n 1 =1.0，n 2 =1.5，u =8.0cm，r =2.0cm，代入单球面折射成像公式，得cm0.2 1.0-.515.1cm 0.80.1=+v得v =12cm，在玻璃棒中离顶点12cm 处成一实像。

11 几何光学一、选择题1、单球面折射成像公式适用的条件为:(A)平行光入射； (B)近轴光线；(C)曲线半径为正；(D)折射率应满足21n n > 。

[ ]2、一圆球形透明体能将无穷远处射来的近轴平行光线会聚于第二折射面的顶点， 则此透明体的折射率为:(A)2； (B)1.3；(C)1.5； (D)1。

[ ]3、某折射率为1.5的平凸透镜，在空气中的焦距为50cm ，则其凸面的曲率半径为:(A)20cm ； (B)50cm ；(C)25cm ； (D)30cm 。

[ ]4、焦度为12D 的放大镜，它的角放大率为:(A)2.08； (B)0.02；(C)2.5； (D)3.0。

[ ]5、人眼可分辨的最短距离为0.1mm ，欲观察0.2m μ的细节，若物镜的线放大率为25，则目镜的焦距应为:(A)2cm ； (B)2.5cm ；(C)1.25cm ； (D)1.75cm 。

[ ]6、某人看不清2.5m 以外的物体，则他需要配戴的眼镜度数应该为:(A)40度； (B)-40度；(C)250度；(D)-250度。

[ ]7、某人看不清1m以内的物体，则他需要配戴的眼镜度数应该为:(A)100度；(B)-100度；(C)300度；(D)-300度。

[ ]8、一折射率为1.5的薄透镜，在空气中的焦距为50cm。

若将它置于折射率为1.4的液体中，则此时透镜的焦距为:(A)150cm；(B)250cm；(C)350cm；(D)500cm。

[ ]9、一个将眼睛紧靠焦距为15cm的放大镜去观察邮票，看到邮票在30cm 远处。

邮票离透镜的距离为:(A)紧靠透镜；(B)10cm；(C)23cm；(D)30cm。

[ ]10、黑板上有两条相距2mm的直线，学生能分辨这两条直线的最大距离为:(A)3.4m；(B)6.88m；(C)13.6m；(D)27.2m。

[ ]11、一架显微镜的物镜焦距为4mm，中间像成在物镜后160mm处，如果目镜的放大倍数是20倍，显微镜总放大率为:(A)200倍；(B)400倍；(C)600倍；(D)800倍。

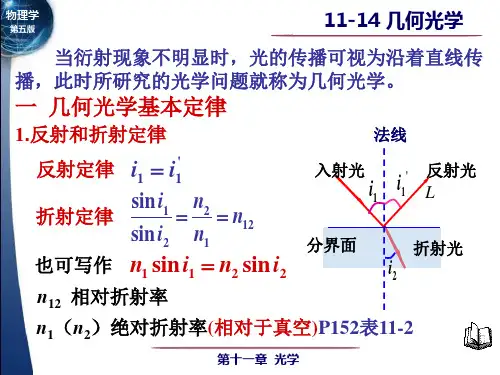
第十一章 波像差前面对像差的讨论是以几何光学为基础的，用光线经过光学系统的实际光路相对于理想光路的偏离来度量的，统称为几何光学。

但光线本身是一抽象的概念，用它的密集程度来评价像质，在很多场合下与实际情况并不符合，而且像差也不可能校正为零。

因此，必须考虑像差的最佳校正方案和像差的容限问题，它与系统的使用要求和使用状况有关。

这些像质评价问题常须基于光的波动本质才能解决。

几何光学中的光线相当于波动光学中波阵面的法线，因此，物点发出的同心光束与球面波对应。

此球面波经过光学系统后，改变了曲率。

如果光学系统是理想的，则形成一个新的球面波，其球心即为物点的理想像点（实际上，由于受系统有限孔径的衍射，即使是理想系统也不可能对物点形成点像）。

但是，实际的光学系统的像差将使出射波面或多或少地变了形，不再为理想的球面波。

这一变了形的实际波面相对于理想球面波的偏离，就是波像差。

波像差与像质评价问题密切相关。

例如要计算斯特列尔强度比（即中心点亮度）和光学传递函数时，就必须求知波像差，而瑞利判断更是直接以波像差的大小来作评价标准的。

加之波像差与几何像差之间有内在联系，利用这种联系，可在一定程度上解决像差的最佳校正问题和容限问题。

§1. 轴上点的波像差对于轴对称光学系统，轴上点发出的球面波经系统以后，只是由于唯一的球差，使出射波面变形而偏离于球面。

由于轴上点波面是轴对称的，其波像差只需从波面与子午平面相截的截线上，取光轴以上的一方来考察即可。

图11－1 轴上点的波像差如图11－1所示，//Z P 是波面的对称轴（即系统的光轴），/P 是系统的出射光瞳中心。

以实际光线与光轴//Z P 的交点/A 为圆心，以r P A =//为半径做圆（实际为球面），即为实际波面。

过/A 点做与光轴成像方孔径角/U 的直线，就是实际光线，设实际光线与实际波面相交于M 点，则r M A =/。

选择光轴上的一点为参考点，例如高斯像点/A ，那么//A A 即为像方孔径角为/U 时的球差：///A A LA =。