当前位置：文档之家 › Matlab教程Ch6 (多项式及其运算)

Matlab教程Ch6 (多项式及其运算)

  • 格式：ppt
  • 大小：1.12 MB
  • 文档页数：34

下载文档原格式

  / 34

合集下载

matlab多项式运算和方程组的求解

matlab多项式运算和方程组的求解

二、多项式（1）多项式的表达式和创建MATLAB中使用一维向量来表示多项式，将多项式的系数按照降幂次序存放在向量中。

例如：多项式2X4+3X3+5X2+1可以用向量[2 3 5 0 1]来表示。

例2-1，输入多项式3x4-10x3+15x+1000在命令窗口输入：p=[3 -10 0 15 1000]输出结果如下：（2）多项式求根1、多项式的根找出多项式的根，即使多项式为零的值，MATLAB提供了特定的函数roots求解多项式的根。

例2-2，求解多项式3x4-10x3+15x+1000的根。

在命令窗口输入：输出的结果如下：2、由根创建多项式在MATLAB中，无论是一个多项式，还是它的根，都是以向量形式存储的，按照惯例，多项式是行向量，根是列向量。

因此当我们给出一个多项式时，MATLAB 也可以构造出相应的多项式，这个过程需要使用函数poly。

例2-3输入及结果（3）多项式四则运算1，多项式的加法MATLAB并未提供一个特别的函数，如果两个多项式向量大小相同，那么多项式相加时就和标准的数组加法相同。

例2-4在命令窗口输入：a=[1 3 5 7 9];b=[1 2 4 6 8];c=a+b输出结果：C（x）=2x4+5x3+9x2+13x+172、多项式的乘法运算在MATLAB中，函数conv支持多项式乘法（运算法则为执行两个数组的卷积）。

例2-5在命令窗口输入：a=[1 3 5 7 9]; b=[1 2 4 6 8];c=conv(a,b)输出的结果如下：C(x)=x8+5x7+15x6+35x5+69x4+100x3+118x2+110x+72PS：conv指令只能进行两个多项式的乘法，两个以上的多项式的乘法需要重复使用conv。

3、多项式的除法运算在MATLAB中，由函数deconv完成的。

例2-6在命令窗口输入：c=[1 5 15 35 69 100 118 110 72];b=[1 2 4 6 8]; [a,r]=deconv (c,b)输出的结果：（4）多项式微分1、多项式的导数MATLAB为多项式求导提供了函数polyder。

matlab多项式运算

matlab多项式运算

在MATLAB中进行多项式运算，可以采用以下方法：1. 表示多项式：在MATLAB中，多项式可以用一个向量表示，向量的元素是多项式的系数，按照降幂排列。

例如，2次多项式2x^2 + 1可以表示为[2 0 1]。

2. 多项式乘法：使用`conv`函数可以进行多项式乘法。

例如，假设有两个多项式p1=[2 0 1]和p2=[3 1]，则可以使用以下命令计算它们的乘积：```matlabp = conv(p1, p2);```这会返回一个新的向量，它是p1和p2的卷积。

3. 多项式除法：使用`deconv`函数可以进行多项式除法，它返回商式和余式。

例如，假设有两个多项式p1=[2 0 1]和p2=[3 1]，则可以使用以下命令计算它们的商式和余式：```matlab[q, r] = deconv(p1, p2);```其中，q是商式，r是余式。

4. 求多项式的根：使用`roots`函数可以求多项式的根。

例如，对于多项式p=[2 0 1]，可以使用以下命令求根：```matlabr = roots(p);```这会返回一个向量，其中包含了多项式的所有根。

5. 求多项式的值：使用`polyval`函数可以求多项式在给定点的值。

例如，对于多项式p=[2 0 1]和点x=1，可以使用以下命令计算多项式的值：```matlabv = polyval(p, 1);```这会返回一个标量值v，它是多项式在x=1处的值。

如果x是一个向量或矩阵，则`polyval`函数会对矩阵或向量中的每一个值求多项式的值。

6. 矩阵多项式求值：使用`polyvalm`函数可以像`polyval`一样求矩阵的值，但要求x为方阵。

例如，对于多项式p=[2 0 1]和方阵x，可以使用以下命令计算多项式在矩阵x中的值：```matlabv = polyvalm(p, x);```这会返回一个矩阵，其中包含了多项式在矩阵x中每一个位置的值。

Matlab教程Ch6

Matlab教程Ch6

12
图形窗口的控制
举例 例题：作出函数y=sin(x)在区间[0，10]上的图形。 x=0:0.01:10; x=0:0.01:10; y=sin(x); h=figure(1); plot(x,y); get(h); set(h,'visible','on'); set(h,'visible','off');
6
设置图形格式
主要有三个方面的设置： （1）线形及其标记的设置。 （2）坐标轴范围、坐标轴标识、网格线的设置。 （3）坐标轴标签、图例、文本等方面的设置。
7
举例
例题 例如： 内作出正弦函数的图形。 例如：在[0，2]内作出正弦函数的图形。 ， 内作出正弦函数的图形 x=0:0.5:2*pi; y=sin(x); plot(x,y,'r:*'); title('sin(x)'); xlabel('x'); ylabel('y'); grid on;
13
6.1 二维图形
plot函数绘制二维曲线，常用格式有： 函数绘制二维曲线，常用格式有： 函数绘制二维曲线
plot(x)：缺省自变量的绘图格式，x可为向量或矩阵。 plot(x, y)：基本格式，x和y可为向量或矩阵。 plot(x1, y1, x2, y2,…)：多条曲线绘图格式，在同一坐 标系中绘制多个图形。 plot(x, y, s)：开关格式，开关量字符串s设定了图形曲 线的颜色、线型及标示符号。 plot(x1, y1, s1,x2, y2,s2,…) 开关格式,多条曲线绘图
23
6.1 二维图形
例题 x=linspace(0,7); y1=sin(2*x); y2=sin(x.^2); y3=(sin(x)).^2; %曲线1：红色实线，+号显示数据点 %曲线2：黑色点线，*号显示数据点 %曲线3：蓝色虚线，上三角形显示数据点 plot(x, y1, 'r+-', x, y2, 'k*:', x, y3, 'b--^')

matlab 求解多项式方程

matlab 求解多项式方程

Matlab求解多项式方程简介多项式方程是数学中常见的方程类型，它由若干个变量的幂次项和常数项组成。

求解多项式方程是数学计算中的基本问题之一，对于复杂的多项式方程，手工求解往往非常困难甚至不可能完成。

而Matlab作为一种强大的科学计算软件，提供了丰富的函数和工具来解决这类问题。

本文将介绍如何使用Matlab求解多项式方程，包括多项式方程的表示方法、求解方法以及具体实现步骤等内容。

多项式方程表示方法多项式方程一般采用以下形式表示：f(x)=a n x n+a n−1x n−1+⋯+a1x+a0其中，a n,a n−1,…,a1,a0为系数，x为变量，n为次数。

在Matlab中，可以使用向量表示系数，例如：coefficients = [a_n, a_{n-1}, ..., a_1, a_0];求解多项式方程的方法Matlab提供了几种不同的方法来求解多项式方程，包括根据系数求解、根据方程求解以及使用符号计算工具箱等方法。

根据系数求解使用roots函数可以根据多项式方程的系数求解方程的根。

该函数的输入参数为系数向量，输出结果为根向量。

coefficients = [a_n, a_{n-1}, ..., a_1, a_0];roots = roots(coefficients);根据方程求解使用solve函数可以根据多项式方程本身求解方程的根。

该函数的输入参数为方程本身，输出结果为根向量。

syms x;equation = a_n*x^n + a_{n-1}*x^{n-1} + ... + a_1*x + a_0;roots = solve(equation, x);使用符号计算工具箱Matlab中的符号计算工具箱提供了更加强大的多项式方程求解功能。

通过定义符号变量，并使用相关函数进行运算，可以得到更加精确和全面的结果。

首先，需要定义符号变量：syms x;然后，可以使用一系列函数进行多项式方程求解，例如：•solve：用于求解代数方程组；•vpasolve：用于数值方式求解代数或者超越方程组；•polyval：用于计算多项式在给定点处的值；•polyfit：用于多项式拟合；•等等。

matlab解多项式方程

matlab解多项式方程

matlab解多项式方程一、引言多项式方程是数学中常见的一类方程，它包含一个或多个未知数，并且每个未知数的指数都是整数。

解多项式方程是求解这个方程中的未知数的值，对于一般的多项式方程，解的求解是一个复杂的过程。

然而，使用MATLAB这样的数学软件，可以大大简化这个过程，提高求解的效率。

本文将介绍如何使用MATLAB解决多项式方程的问题。

二、MATLAB解多项式方程的方法MATLAB提供了多种方法来解决多项式方程的问题，包括求解代数方程的根、求解多项式方程的特殊解等。

下面将介绍几种常见的方法：1. 使用roots函数求解代数方程的根roots函数是MATLAB中用于求解代数方程的根的函数，对于给定的多项式方程，它可以返回该方程的所有根。

使用方法如下：p = [1, -3, 2];r = roots(p);上述代码中，p是一个向量，表示一个多项式方程的系数，r是一个向量，表示该方程的所有根。

例如，对于多项式方程x^2 - 3x + 2 = 0，p表示的向量是[1, -3, 2]，r表示的向量是[1, 2]，即方程的根是1和2。

2. 使用poly函数求解多项式方程的特殊解poly函数是MATLAB中用于求解多项式方程的特殊解的函数，它可以根据给定的根来返回对应的多项式方程的系数。

使用方法如下：r = [1, 2];p = poly(r);上述代码中，r是一个向量，表示一个多项式方程的根，p是一个向量，表示该方程的系数。

例如，对于多项式方程的根是1和2，r表示的向量是[1, 2]，p表示的向量是[1, -3, 2]，即方程的系数是1、-3、2.三、MATLAB解多项式方程的示例为了更好地理解MATLAB解多项式方程的方法，下面将通过一个示例来演示具体的步骤：1. 求解一元二次方程假设我们要求解方程x^2 - 3x + 2 = 0的根，我们可以使用roots函数来实现：p = [1, -3, 2];r = roots(p);运行上述代码后，我们可以得到方程的根r是[1, 2]。

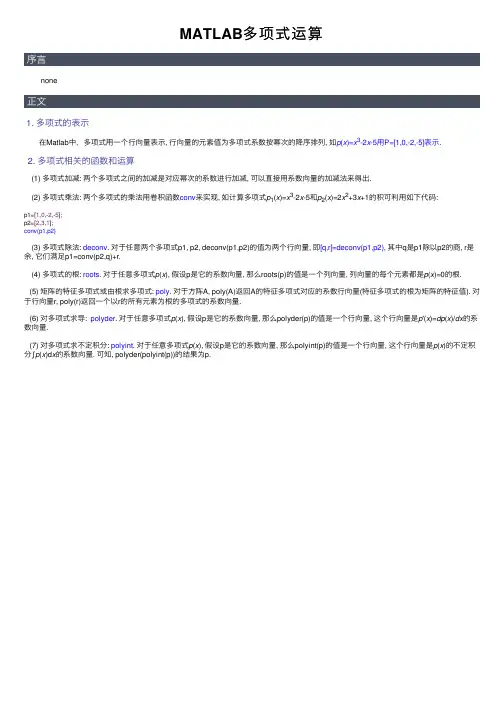
MATLAB多项式运算

MATLAB多项式运算

MATLAB多项式运算 none1. 多项式的表⽰ 在Matlab中，多项式⽤⼀个⾏向量表⽰, ⾏向量的元素值为多项式系数按幂次的降序排列, 如p(x)=x3-2x-5⽤P=[1,0,-2,-5]表⽰.2. 多项式相关的函数和运算　(1) 多项式加减: 两个多项式之间的加减是对应幂次的系数进⾏加减, 可以直接⽤系数向量的加减法来得出.　(2) 多项式乘法: 两个多项式的乘法⽤卷积函数conv来实现, 如计算多项式p1(x)=x3-2x-5和p2(x)=2x2+3x+1的积可利⽤如下代码:p1=[1,0,-2,-5];p2=[2,3,1];conv(p1,p2)　(3) 多项式除法: deconv. 对于任意两个多项式p1, p2, deconv(p1,p2)的值为两个⾏向量, 即[q,r]=deconv(p1,p2), 其中q是p1除以p2的商, r是余, 它们满⾜p1=conv(p2,q)+r.　(4) 多项式的根: roots. 对于任意多项式p(x), 假设p是它的系数向量, 那么roots(p)的值是⼀个列向量, 列向量的每个元素都是p(x)=0的根.(5) 矩阵的特征多项式或由根求多项式: poly. 对于⽅阵A, poly(A)返回A的特征多项式对应的系数⾏向量(特征多项式的根为矩阵的特征值). 对于⾏向量r, poly(r)返回⼀个以r的所有元素为根的多项式的系数向量.(6) 对多项式求导: polyder. 对于任意多项式p(x), 假设p是它的系数向量, 那么polyder(p)的值是⼀个⾏向量, 这个⾏向量是p'(x)=dp(x)/dx的系数向量.(7) 对多项式求不定积分: polyint. 对于任意多项式p(x), 假设p是它的系数向量, 那么polyint(p)的值是⼀个⾏向量, 这个⾏向量是p(x)的不定积分∫p(x)d x的系数向量. 可知, polyder(polyint(p))的结果为p.。

第6章MATLAB数据分析与多项式计算

第6章MATLAB数据分析与多项式计算

第6章MATLAB数据分析与多项式计算MATLAB是一种面向科学和工程计算的计算机语言和环境。

它具有强大的数据分析和多项式计算功能，可以用于数据处理、统计分析、曲线拟合、插值计算、解方程等多种应用。

数据分析是从数据中提取有用信息的过程，其中使用MATLAB可以轻松地进行各种数据操作和分析。

MATLAB提供了各种统计分析函数，可以计算数据的统计特征，如均值、方差、标准差、相关系数等。

同时，它还提供了数据绘图功能，可以将数据以直方图、散点图、折线图等形式展示出来，帮助用户更好地理解数据。

多项式计算是利用多项式进行数值计算的过程。

在MATLAB中，可以使用多种方法进行多项式计算，如多项式加减乘除、多项式求值、多项式插值等。

MATLAB提供了丰富的多项式操作函数，可以方便地进行多项式运算和计算。

在数据分析中，多项式计算经常用于曲线拟合和插值计算。

曲线拟合是根据给定的数据点，找出一个与之最接近的曲线。

MATLAB提供了polyfit函数，可以根据给定的数据点和多项式阶数，自动拟合出最优的多项式曲线。

此外，MATLAB还提供了curvefit函数，可以进行更加复杂的曲线拟合，如指数曲线拟合、对数曲线拟合等。

插值计算是根据已知的数据点，通过插值方法找出在这些数据点之间的未知点的近似值。

MATLAB提供了interp1函数，可以根据给定的数据点和插值方法，自动进行插值计算。

此外，MATLAB还提供了interp2函数，可以进行二维插值计算。

除了数据分析和多项式计算功能，MATLAB还具有其他强大的数值计算功能，如数值积分、数值微分、解线性方程组等。

这些功能使得MATLAB成为科学与工程领域中常用的计算工具。

在使用MATLAB进行数据分析和多项式计算时，需要注意数据的有效性和合理性。

数据分析的结果只能作为参考，不能作为绝对的判断依据。

多项式计算的结果也可能存在误差，需要进行适当的精度控制。

总之，MATLAB是一款功能强大的数据分析和多项式计算工具，可以帮助科学家和工程师快速、准确地进行各种数值计算和分析任务。

matlab符号运算 多项式

matlab符号运算 多项式

matlab符号运算多项式（实用版）目录1.MATLAB 中的多项式运算2.MATLAB 中的符号运算3.字符数组和 ASCII 码4.创建二维字符数组5.单元数组和字符串6.判断字符串是否相等正文在 MATLAB 中，多项式运算是一个非常常用的功能。

多项式运算的函数通常以向量来表示，这与符号表达式有所不同。

在 MATLAB 中，你可以使用符号运算来处理代数表达式，这种运算允许运算对象包含非数值的符号变量。

在 MATLAB 中，字符串可以用字符数组来表示，而字符数组则与ASCII 码相对应。

每个字符都有两个字节来构成。

你可以使用 whos 函数来查看字符数组。

如果想要将字符串转换为它的 ASCII 码，可以使用double 函数；如果想将 SACII 码转换为原来的字符，可以使用 char 函数。

当你需要创建二维的字符数组时，需要先确定数组的每一行字符的个数都必须相等。

例如，你可以使用 name 函数创建一个二维字符数组，如"Thomas R.Lee";"Sr.Developer"。

在 MATLAB 中，你可以通过利用单元数组来保存字符串的数据，这比字符串数组更加方便。

你可以使用 cellstr 函数将字符数组转换为单元数组。

当需要判断两个字符串是否相等时，MATLAB 提供了两个函数：strcmp 和 strncmp。

strcmp 函数用于比较两个输入字符串是否相等，而 strncmp 函数用于比较两个输入字符串的前几个字符是否相等。

总的来说，MATLAB 提供了强大的多项式运算和符号运算功能，同时它也提供了方便的字符数组和 ASCII 码转换功能，以及字符串的创建和比较功能。

Matlab中多项式的运算

Matlab中多项式的运算

Matlab中多项式的运算1:直接键入p=[ 1 2 3 4]系统就自动建立起多项式y=x3+2x2+3x+42:利用roots(p)命令就可以求解这个多项式的根,例如：>> p=[1 2 3 4 ];>> roots(p)ans = -1.6506-0.1747 + 1.5469i-0.1747 - 1.5469i3：利用poly(a)命令可以由多项式的根求解多项式的系数，其中a=[ 2 3]的表示形式。

例如：>> a=[2 3];>> poly(a)ans = 1 -5 6则这个多项式为x2+5x+6.4：多项式的相加减：若干个多项式相加减时就是把它们的系数数组直接相加减，但是系数数组元素的个数必须相等，若不够，可以补0，例如：a=[1 2 3 4];b=[2 2 1 2];c=a+bc =[ 3 4 4 6]5：利用conv(a,b)命令可以求解a,b两个多项式的乘积。

例如：>> a=[1 2];>> b=[1 -2];>> c=conv(a,b)c = 1 0 -4.因为a=x+2,b=x-2,所以a,b的乘积为c=x2-4.6:利用polyder(a)命令可以去、求多项式的微分（求导数），例如：>> a=[1 2 0 -5 6]; >> b=polyder(a)b =4 6 0 -5,其中a=x4+2x3-5x+6;b=4x3+6x2-5.6;给出x的范围，利用polyval(a)命令可以求出x对应的多项式的值，例如：>> x=-1:0.1:2;>> a=[1 2 0 -5 6];>> y=polyval(a,x);>> plot(x,y)>> grid 绘图结果如下：。

matlab中进行多项式运算的一般步骤

matlab中进行多项式运算的一般步骤

在使用MATLAB进行多项式运算时，一般可以遵循以下几个步骤：1. 创建多项式我们需要创建多项式。

在MATLAB中，可以使用`poly`函数来创建多项式。

如果我们要创建一个多项式3x^3+2x^2-5x+4，可以使用以下命令：```matlabp = [3, 2, -5, 4];```其中，`p`即为所创建的多项式。

通过上述命令，MATLAB会将多项式系数按照从高次到低次的顺序存储在数组`p`中。

2. 求多项式的根求多项式的根是多项式运算中常见的操作。

在MATLAB中，可以使用`roots`函数来求多项式的根。

对于上述创建的多项式`p`，可以使用以下命令求其根：```matlabr = roots(p);```其中，`r`即为所求得的多项式的根。

通过上述命令，MATLAB会返回多项式的根，并存储在数组`r`中。

3. 多项式求导多项式求导是指对多项式进行微分操作。

在MATLAB中，可以使用`polyder`函数来对多项式进行求导。

对于上述创建的多项式`p`，可以使用以下命令对其进行求导：```matlabdp = polyder(p);```其中，`dp`即为所求得的多项式的导数。

通过上述命令，MATLAB会返回多项式的导数，并存储在数组`dp`中。

4. 多项式积分多项式积分是指对多项式进行积分操作。

在MATLAB中，可以使用`polyint`函数来对多项式进行积分。

对于上述创建的多项式`p`，可以使用以下命令对其进行积分：```matlabP = polyint(p);```其中，`P`即为所求得的多项式的积分。

通过上述命令，MATLAB会返回多项式的积分，并存储在数组`P`中。

5. 多项式加减乘除在MATLAB中，可以使用`polyadd`、`polysub`、`polymul`和`polydiv`函数来进行多项式的加减乘除运算。

对于两个多项式`p1`和`p2`，可以使用以下命令进行加减乘除运算：```matlabp_sum = polyadd(p1, p2);p_diff = polysub(p1, p2);p_product = polymul(p1, p2);[p_quotient, p_rem本人n] = polydiv(p1, p2);```通过上述命令，MATLAB会返回多项式的和、差、积、商和余数，并存储在相应的数组中。

matlab计算多项式

matlab计算多项式

matlab计算多项式
Matlab是一款强大的数学计算软件，可以用于解决各种数学问题，包括多项式计算。

在Matlab中，我们可以使用多种方法计算多项式，如使用多项式函数、向量运算、循环和递归等。

一种常用的方法是使用多项式函数，Matlab中有多种多项式函数可供使用，例如polyval函数可以计算多项式函数在给定点的值。

使用polyfit函数可以拟合多项式函数，并返回多项式系数的向量。

同时，还可以使用polyder函数求解多项式的导数，使用polyint函数求解多项式的积分。

除了使用多项式函数，我们还可以使用向量运算计算多项式。

例如，我们可以将多项式的系数存储在一个向量中，然后使用Matlab 中的向量运算函数计算多项式的值。

例如，使用dot函数可以计算向量之间的点积，而使用cross函数可以计算向量之间的叉积。

在某些情况下，循环和递归也可以用于计算多项式。

例如，我们可以使用for循环计算多项式的值，或使用递归函数计算多项式的系数。

这种方法通常需要更多的代码和计算时间，但可以处理更复杂的多项式。

总之，在Matlab中计算多项式有多种方法，我们可以根据问题的需求选择适合的方法。

无论使用哪种方法，我们都可以利用Matlab 强大的计算能力轻松地计算多项式，并解决各种数学问题。

- 1 -。

MATLAB编程与工程应用——第6章 MATLAB数据分析与多项式计算

MATLAB编程与工程应用——第6章 MATLAB数据分析与多项式计算

MATLAB数据分析与多项式计算
二、二维数据插值
某实验对一根长10 10米的钢轨进行热源的温度传播测 例6.10 某实验对一根长10米的钢轨进行热源的温度传播测 表示测量点0:2.5:10( 0:2.5:10(米 试。用x表示测量点0:2.5:10(米)，用h表示测量时间 0:30:60(秒 表示测试所得各点的温度(℃) (℃)。 0:30:60(秒)，用T表示测试所得各点的温度(℃)。试用 线性插值求出在一分钟内每隔20 20秒 钢轨每隔1 线性插值求出在一分钟内每隔20秒、钢轨每隔1米处的温 TI。 度TI。 命令如下： x=0:2.5:10; h=[0:30:60]'; T=[95,14,0,0,0;88,48,32,12,6;67,64,54,48,41]; xi=[0:10]; hi=[0:20:60]'; TI=interp2(x,h,T,xi,hi) exp6_10.m
MATLAB数据分析与多项式计算
6.2 数据插值
二、二维数据插值
z1=interp2(x,y,z,x1,y1,'method') 其中x,y是两个向量，分别描述两个参数的采样点， z是与参数采样点对应的函数值， x1,y1是两个向量或标量，描述欲插值的点。 z1是根据相应的插值方法得到的插值结果。 method的取值与一维插值函数相同。 x,y,z也可以是矩阵形式。 x1,y1的取值范围不能超出x,y的给定范围，否则，会给 出“NaN”错误。
MATLAB数据分析与多项式计算
MATLAB数据分析与多项式计算
一、最大值和最小值
格式3 3. 格式3 U=max(x,y) U=min(x,y) 如果x为标量，则y可为标量、向量或矩阵 如果x为向量或矩阵，则y可为标量或与x同维的向量或 矩阵 x,y是两个同型的向量或矩阵，结果U是与x,y同型的向 量或矩阵，U的每个元素等于x,y对应元素的较大/小者。 如果y是一个标量，结果U是与x同型的向量或矩阵，U 的每个元素等于x对应元素和y中的较大/小者。 例6.3 求两个2×3矩阵x, y所有同一位置上的较大元素 求两个2 矩阵x, y所有同一位置上的较大元素 构成的新矩阵p 构成的新矩阵p。exp6_3.m

第六讲：Matlab多项式和代数方程求解器

第六讲：Matlab多项式和代数方程求解器
x= -0.1819 -1.6630 2.2172 -0.4467
线性方程组的解析解
linsolve(A,b)：解线性方程组 Ax b
例：解方程组
x
2yz xz3
2
x 3y 8
>> A=[1 2 –1; 1 0 1; 1 3 0]; >> b=[2;3;8]; >> x=linsolve(A,b)
Matlab 没有提供专门进行多项式加减运算的函数，事实 上，多项式的加减就是其所对应的系数向量的加减运算
对于次数相同的多项式，可以直接对其系数向量进行 加减运算；
如果两个多项式次数不同，则应该把低次多项式中系 数不足的高次项用 0 补足，然后进行加减运算。
例： p1 2x3 x2 3
p2 2x 1 p1 p2 2x3 x2 2x 4
Matlab 多项式运算 与代数方程求解器
Matlab 多项式运算
Matlab 中多项式的表示方法
在 Matlab 中，n 次多项式是用一个长度为 n+1的向量来 表示，缺少的幂次项系数为 0。
p( x) an x n an1x n1 a1x a0 在 Matlab中表示为向量：[an ,an1, ,a1,a0 ]
1.恰定方程组的解
方程ax=b(a为非奇异) x=a-1 b 矩阵逆
两种解: x=inv(a)b — 采用求逆运算解方程 x=a\b — 采用左除运算解方程
例: x1+2x2=8 2x1+3x2=13
方程ax=b
1 2
2 3
x1
x
2
=
8 13
a x=b
a=[1 2;2 3];b=[8;13];

matlab语言多项式计算的分析与概述

matlab语言多项式计算的分析与概述

matlab语言多项式计算的分析与概述1、多项式的表示在MATLAB中创建多项式向量时，注意三点:(1)多项式系数向量的顺序是从高到低。

(2)多项式系数向量包含0次项系数，所以其长度为多项式最高次数加1。

(3）如果有的项没有，系数向量相应位置应用0补足。

2、多项式的四则运算(1)多项式的加减运算多项式的加减运算非常简单，即相应向量相加减。

(2)多项式乘法conv (P1,P2):多项式相乘函数。

在这里，P1、P2是两个多项式系数向量。

(3）多项式除法[Q,r]=deconv(P1,P2):多项式相除函数。

其中，Q返回多项式P1除以P2的商式，r返回P1除以P2的余式。

这里，Q和r仍是多项式系数向量。

deconv是conv的逆函数，因此有Pl=conv(Q,P2)+r即商式(Q)乘以除式(P2)加止余式( r)等手被除式(P1)> > f = [ 3 - 5 0 - 7 5 6 ] ; g = [ 3 5 - 3 ] ; g1 = [ 0 0 0 g ] ; y1= f + g1 % 多项式相加 , 等长向量可加减 y1 = 3 - 5 0 - 4 10 3 > > y2 = f - g1 % 多项式相减 y2 = 3 - 5 0 - 10 0 9 > > y3 = conv ( f ,g ) % 多项式相乘，积向量的长度为两个因子向量的长度之和减 1 y3 = 9 0 - 34 - 6 - 20 64 15 - 18 > > [ y4 r ] = deconv ( f , g ) % 多项式相除，y4是商式，r是余式 y4 =1.0000 -3.33336.5556 -16.5926 r = 0 0 0 0107.6296 -43.7778 > > y5 = conv ( y4 , g ) + r % 商式乘以除式加上余式 , 看看是否与被除式f相等 y5 =3.0000 -5.0000 0 -7.00005.00006.0000补充：三个或者三个以上的多项式相乘可用以下方法syms y1 y2 y3 x y1 = x ^ 2 + 5 * x + 2 ; y2 = - 2 * x ^ 2 + 2 * x - 3 ; y3 = 9 * x + 7 ; ans = y1 * y2 * y3 ; disp ( ans ) % 显示的结果没有展开 ans1 = expand ( ans ) % 使用expand函数将结果展开ans2 = factor ( ans ) % 将多项式因式分解% % 运行结果 ans = - ( 9 * x + 7 ) * ( x ^ 2 + 5 * x + 2 ) * ( 2 * x ^ 2 - 2 * x + 3 ) ans1 = - 18 * x ^ 5 - 86 * x ^ 4 - 29 * x ^ 3 - 78 * x ^ 2 - 131 * x - 42 ans2 = [ - 1 , 9 * x + 7 , x ^ 2 + 5 * x + 2 , 2 * x ^ 2 - 2 * x + 3 ]3、多项式的求导polyder( ):多项式求导函数。

MATLAB语言基础 ch6数值计算

MATLAB语言基础 ch6数值计算

5.2.1 矩阵运算和特征参数
1. 矩阵运算 2. 矩阵的标量特征参数
秩 迹 行列式
rank(A) trace(A) det(A)
5.2.2 矩阵的变换和特征值分解
[R,ci]=rref(A)
借助初等变换把A变换成行阶梯矩阵 借助初等变换把 变换成行阶梯矩阵R 变换成行阶梯矩阵
X= null(A)
• • • • • • • • • • • • x=[1 8 4 2;9 6 2 5;3 6 7 1] % 产生一个二维数组 产生一个二维数组x x= 1 8 4 2 9 6 2 5 3 6 7 1 y0=median(x) % 按列操作 y0 = 3 6 4 2 y1=median(x,1) % 此时 此时DIM=1,故按列操作 结果 为行 故按列操作,结果 故按列操作 结果y1为行 向量 y1 = 3 6 4 2 y2=median(x,2) % 此时 此时DIM=2,故按行操作 结果 为列 故按行操作, 故按行操作 结果y2为列 向量 y2 = 3.0000 5.5000 4.5000
的平均值赋予行向量Y。 若 X为向量 ， 则 Y为单变量 。 为向量， 为单变量。 的平均值赋予行向量 。 为向量 为单变量
• Y= mean(X,DIM)：按数组 的第 的第DIM维的方向 ：按数组X的第 维的方向
的元素求其平均值赋予向量Y。 的元素求其平均值赋予向量 。若DIM=1，为按列操 ， 为二维数组， 为 作 ； 若 DIM=2，为按行操作 。 若 X为二维数组， Y为 ， 为按行操作。 为二维数组 一个向量； 为一维数组， 为单变量。 一个向量；若X为一维数组，则Y为单变量。 为一维数组 为单变量
（2）自变量的增量选取一定要大于原数据 ） 相对精度的10倍以上 相对精度的 倍以上 • （3）尽量使用 ）尽量使用Matlab提供的现成指令 提供的现成指令 • • Dx=diff(X) 求差分 • FX=gradient(F) 求一元函数梯度 • [FX,FY]=gradient(F) 求二元函数梯度

MATLAB-ch6_编程

MATLAB-ch6_编程

1/5
1/6
1/7
1/8
1/5
1/6
1/7
1/8
1/9
3）
%
clear
tic
%
K=1000;
for m = 1:K
for n = 1:K
A1(m,n) = 1/(m+n -1);
end
end
t1=toc
%
t1 =
17.434
%
tic
K=1000;
A2 = zeros(K,K);
%
for m = 1:K
'及格' '良好'
'不及格' '优秀' '满分'
〖说明〗
6.1.3for 循环和 while 循环
for ix=array
for 循环
表 6.1-3 循环结构的使用方式 while 循环
while expression
(commands) end
(commands) end
【例 6.1-3】创建 Hilbert 矩阵。
双分支
多分支
if expr (commands1)
else (commands2)
end
if expr1 (commands)
elseif expr2 (commands) …….
else (commandsk)
end
【例 6.1-1】
1） function [xmin,fmin,n]=exm060101(fx,a,b,Nt) % exm060101.m % fx % a、b % Nt % xmin、ymin %n
for n = 1:K
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
16
例．用以上4种方法对y cos x在[0,6]上的一维插值效果 进行比较.
17
1 例．用以上4种方法对y ( x [2, 2])选用11个数据点 2 2 x 进行插值并画图比较结果.
>> x=-2:4/(11-1):2; >> y=1./(2+x.^2); >> xi=-2:0.1:2; >> y1=interp1(x,y,xi,’*nearest’); >> y2=interp1(x,y,xi,’*linear’); >> y3=interp1(x,y,xi,’*spline’); >> y4=interp1(x,y,xi,’*cubic’); >> subplot(2,2,1),plot(x,y,’rp’,xi,y1),title(‘nearest’) >> subplot(2,2,2),plot(x,y,’rp’,xi,y2),title(‘linear’) >> subplot(2,2,3),plot(x,y,’rp’,xi,y3),title(‘spline’) >> subplot(2,2,4),plot(x,y,’rp’,xi,y4),title(‘cubic’)
21
22
23
输入方式
变量＝input(‘提示符号串’) 如：x=input(‘x=’); y=input(‘please input y=’); 输出方式 （1）直接输出 x %变量后无分号“;”,变量直接输出 disp([a]) %可以是标量、向量、矩阵 （2）格式控制输出 fprintf(‘x=%.3f,s=%.0f\n',a,b)
18
nearest 0.5 0.4 0.3 0.2 0.1 -2 0.5 0.4 0.3 0.2 0.1 -2
linear
-1
0 spline
1
2
-1
0 cubic
1
2
0.5 0.4 0.3 0.2 0.1 -2
0.5 0.4 0.3 0.2 0.1 -2
-1
0
1
2
-1
0
1
2
19
二维多项式插值： yi=interp2(x,y,z,xi,yi,method) 已知同维数据点x、y和z，运用method指定的方法（要 在单引号之间写入）计算插值点(xi,yi)处的数值zi. Method指定的方法同一维多项式插值.
ans = 1.0000 -5.0000 -2.0000
即
1
3
2 2 5 2 4
4
多项式求根
r=roots(p) 求多项式p（用系数行向量）表示的根.
例：求多项式f ( x ) x 3 6 x 2 72 x 27的根.
>>p=[1 -6 -72 -27]; >>r=roots(p)
14
插值
在离散数据的基础上补插连续函数，使得这条连续曲线 通过全部给定的离散数据点。插值是离散函数逼近的重 要方法，利用它可通过函数在有限个点处的取值状况， 估算出函数在其他点处的近似值。 插值和拟合 相同之处：寻找一条“光滑”的曲线将已知数据点连贯起来 不同之处：拟合点曲线不要求一定通过数据点 插值的曲线要求必须通过数据点

[q,r]=deconv(P1,P2)
多项式P1和P2作除法运算, q为商，r
为余数
>> [q, r] = deconv(c, a) %多项式c和a作除法运算 q= 2 0 -1 r= 0 0 0 0
8
多项式的求导
polyder(p)
对多项式p求导
>> q = polyder(p)
q= 3 0 -2
运行结果： r= 12.1229 -5.7345 -0.3884
5
多项式求值
y=polyval(p,X) X可以是向量也可以是矩阵. >> polyval(p,5) %按数组规则计算5处多项式的值 ans = 110 >> subs(sym_p,5) % 符号变量代值 ans = 110 >> X = [2 4 5; -1 0 3; 7 1 5]; >> Y = polyvalm(p, X) %按矩阵规则计算X处多项式的值 Y= 377 179 439 111 81 136 490 253 639
3
生成多项式
>> p = [1 0 -2 -5]
3 x 2x 5 %表示多项式
>> r = [0, 1, -1]; poly(r) %生成多项式 x( x 1)( x 1) 根为 0,1,-1 ans = 1 0 -1 0
>> a = [1 2; 3 4]; poly(a) % 生成矩阵的特征多项式
如：fprintf(‘x=%.5f,y=%.0f\n',pi,sqrt(2));
x=3.14159,y=1
2018/10/10 24
流程控制

程序流程控制包含控制程序的基本结构和语法 结构化的程序主要有三种基本的程序结构 顺序结构 指所有组成程序源代码的语句按照由上至下的次序 依次执行，直到程序的最后一个语句。 选择结构 依照不同的判断条件进行判断，然后根据判断的结 果选择某一种方法来解决某一个问题。 循环结构 就是在程序中某一条语句或多条语句重复多次的运 行。 MATLAB语言的程序结构与其它高级语言是一致的，分 为顺序结构、选择结构、循环结构
【例】用一个5次多项式在区间[0，2π]内逼近函数sin(x)
X=linspace(0,2*pi,50);Y=sin(X); [P,S]=polyfit(X,Y,5) %得到5次多项式的系数和误差 plot(X,Y,‘r*',X,polyval(P,X))
10
11
例．现有一组实验数据：x的取值是从1到2之间的数，间隔 为0.1，y的取值为2.1, 3.2, 2.1, 2.5, 3.2, 3.5, 3.4,4.1,4.7,5.0,4.8. 要求分别用二次、三次和七次拟合曲线来拟合这组数据， 观察这三组拟合曲线哪个效果更好？
1
第六章 多项式及其运算
多项式的表示方式
若f ( x )为一n次一元多项式，则 f ( x ) an x n a1 x a0 在Matlab中使用行向量来表示多项式的系数，并按自变量x 的幂次由高到低的顺序排列出相应的系数. 如多项式f ( x ) an x n a1 x a0的系数向量为: a n a n 1 a 0 若缺项，则其对应项的系数用0补齐.
15
例．用以上4种方法对y cos x在[0,6]上的一维插值效果 进行比较.
x=0:6; y=cos(x);
xi=0:0.25:6;
yi1=interp1(x,y,xi,'*nearest') yi2=interp1(x,y,xi,'*linearபைடு நூலகம்) yi3=interp1(x,y,xi,'*spline') yi4=interp1(x,y,xi,'*cubic') plot(x,y,'ro',xi,yi1,'+', xi,yi2,'-', xi,yi3,'k.-', xi,yi4,'m:') legend('原始数据','最近点插值','线性插值','样条插值','立 方插值')
( x 2x 5)
3
>> a = [1 3 5]; b = [2 4 6]; >> c = polyder(a,b) %多项式a,b乘积的导数
c= 8 30 56 38
( x 2 3x 5) q( x) (2 x 2 4 x 6) d ( x)
2
将多项式的行向量转化为相应的一般多项式的命令形式如下： poly2str(p,'x') 或 poly2sym(p)
例 : 输出多项式f ( x ) x 4 5 x 3 3 x 1的一般表达式.
>> p=[1 5 0 -3 1]; >> f=poly2str(p,’x’) >> sym_p = poly2sym(p) f= x^4 + 5 x^3 - 3 x + 1 sym_p = x^4+5*x^3-3*x+1
20
例．f 用以上4种方法对z xe 效果进行比较.
( x2 y2 )
在[2, 2]上的二维插值
>> [x,y]=meshgrid(-2:0.5:2); >> z=x.*exp(-x.^2-y.^2); >> [x1,y1]=meshgrid(-2:0.1:2); >> z1=x1.*exp(-x1.^2-y1.^2); >> figure(1) >> subplot(1,2,1),mesh(x,y,z),title('数据点') >> subplot(1,2,2),mesh(x1,y1,z1),title('函数图象') >> [xi,yi]=meshgrid(-2:0.125:2); >> zi1=interp2(x,y,z,xi,yi,'*nearest'); >> zi2=interp2(x,y,z,xi,yi,'*linear'); >> zi3=interp2(x,y,z,xi,yi,'*spline'); >> zi4=interp2(x,y,z,xi,yi,'*cubic'); >> figure(2) >> subplot(2,2,1),mesh(xi,yi,zi1),title('最近点插值') >> subplot(2,2,2),mesh(xi,yi,zi2),title('线性插值') >> subplot(2,2,3),mesh(xi,yi,zi3),title('样条插值') >> subplot(2,2,4),mesh(xi,yi,zi4),title('立方插值')