结构力学第九章习题及参考答案大题

《结构力学习题》(含答案解析)本页仅作为文档封面，使用时可以删除This document is for reference only-rar21year.March20 第三章 静定结构的位移计算一、判断题：1、虚位移原理等价于变形谐调条件，可用于求体系的位移。

2、按虚力原理所建立的虚功方程等价于几何方程。

3、在非荷载因素(支座移动、温度变化、材料收缩等)作用下，静定结构不产生内力，但会有位移且位移只与杆件相对刚度有关。

4、求图示梁铰C 左侧截面的转角时，其虚拟状态应取：A.;; B.D.M C.=1=1=15、功的互等、位移互等、反力互等和位移反力互等的四个定理仅适用于线性变形体系。

6、已知M p 、M k 图，用图乘法求位移的结果为：()/()ωω1122y y EI +。

M kM p 21y 1y 2**ωω( a )M =17、图a 、b 两种状态中，粱的转角ϕ与竖向位移δ间的关系为：δ=ϕ 。

8、图示桁架各杆E A 相同，结点A 和结点B 的竖向位移均为零。

Aa a9、图示桁架各杆EA =常数，由于荷载P是反对称性质的，故结点B的竖向位移等于零。

2121二、计算题：10、求图示结构铰A 两侧截面的相对转角ϕA ，EI = 常数。

q l l l /211、求图示静定梁D 端的竖向位移 ∆DV 。

EI = 常数 ，a = 2m 。

a a a 10kN/m12、求图示结构E 点的竖向位移。

EI = 常数 。

l l l /3 2 /3/3q13、图示结构，EI=常数 ，M =⋅90kN m , P = 30kN 。

求D 点的竖向位移。

P 3m 3m 3m14、求图示刚架B 端的竖向位移。

q15、求图示刚架结点C 的转角和水平位移，EI = 常数 。

q16、求图示刚架中Ｄ点的竖向位移。

EI ＝常数。

l ll/217、求图示刚架横梁中Ｄ点的竖向位移。

EI＝常数。

18、求图示刚架中D点的竖向位移。

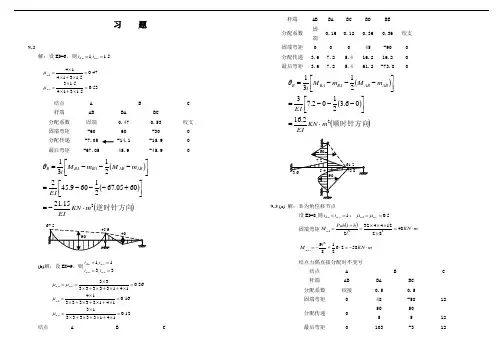
习 题9-2解：设EI=6，则5.1,1==BC AB i i 53.05.13145.1347.05.131414=⨯+⨯⨯==⨯+⨯⨯=BC BA μμ结点 A BC 杆端 AB BA BC 分配系数 固端 0.47 0.53 绞支 固端弯矩 -60 60 -30 0 分配传递 -7.05 -14.1 -15.9 0 最后弯矩-67.0545.9-45.9()()()逆时针方向215.216005.6721609.4522131m KN EI EI m M m M i AB AB BA BA B ⋅-=⎥⎦⎤⎢⎣⎡+---=⎥⎦⎤⎢⎣⎡---=θ(b)解：设EI=9，则3,31,1====BE BD BC AB i i i i12.0141333331316.0141333331436.01413333333=⨯+⨯+⨯+⨯⨯==⨯+⨯+⨯+⨯⨯==⨯+⨯+⨯+⨯⨯==BC BA BE BD μμμμ结点 A BC杆端 AB BA BC BD BE 分配系数 固端 0.16 0.12 0.36 0.36 绞支 固端弯矩0 45 -90 0 分配传递 3.6 7.2 5.4 16.216.20 最后弯矩 3.6 7.25.461.2 -73.8()()()顺时针方向22.1606.32102.732131m KN EI EI m M m M i AB AB BA BA B ⋅=⎥⎦⎤⎢⎣⎡---=⎥⎦⎤⎢⎣⎡---=θ9-3 (a) 解：Ｂ为角位移节点设EI=8,则1==BC AB i i ，5.0==BC BA μμ 固端弯矩()m KN l b l Pab M BA ⋅=⨯⨯⨯⨯=+=4882124432222 m KN l M BC ⋅-=⋅+-=582621892 结点力偶直接分配时不变号结点 A BC 杆端 AB BA BC 分配系数 铰接 0.5 0.5 固端弯矩 0 48 -58 12 分配传递0 50 50 5 5 12 最后弯矩103-312(b) 解：存在B 、C 角位移结点设EI=6，则1===CD BC AB i i i73741413145.0141414==⨯+⨯⨯==⨯+⨯⨯==BC CB BC BA μμμμ固端弯矩：mKN M M M m KN M m KN M CDCB BC BA AB ⋅-=⨯+⨯-===⋅-=⋅-=14021808640080802结点 A BC杆端 AB BA BC CB CD 分配系数 固结 0.5 0.5 4/7 3/7 固端弯矩-80 80 0 0 -140 分配传递-20 -40 -40 -2047.5 91.4 68.6 -11.4 -22.8 -22.8 -11.4 3.25 6.5 4.9 -0.82-1.63-1.63-0.820.6 0.45 最后弯矩-112.2215.57-15.4866.28-66.05(c) 解：B 、C 为角位移结点51411,5441454414,51411=+==+==+==+=CD CBBC BA μμμμ固端弯矩：mKN M mKN M mKN M mKN M mKN M mKN M DC CD CB BC BA AB ⋅-=⨯-=⋅-=⨯-=⋅=⨯=⋅-=⨯-=⋅=⨯=⋅=⨯=10065242003524501252450125241283424646424222222结点 A BCD 杆端 AB BA BC CB CD 滑动 分配系数 滑动 0.2 0.8 0.8 0.2 -100固端弯矩64 128 -50 50 -200 分配传递15.6 -15.6 -62.4 -31.272.48 144.96 36.24 -36.24 14.5 -14.5 -58 -29 11.6 23.2 5.8 -5.8 2.32-2.32-9.28-4.643.7 0.93 -0.93 最后弯矩96.4295.58-95.6157.02-157.03-142.9796.42(d) 解：11313141413114131414145.0141414=⨯+⨯+⨯⨯===⨯+⨯+⨯⨯===⨯+⨯⨯=DBDE DCCD CA μμμμμ 固端弯矩：mKN M mKN M ED DE ⋅=⋅-=⨯-=383812422 结点 A CD E 杆端 AC CA CD DC DB DE ED 分配系数 固结 0.5 0.5 4/11 3/11 4/11 固结 固端弯矩0 0 0 0 0 -2.67 2.67 分配传递-5 -10 -10 -546/33 92/33 69/33 92/33 46/33 -0.35 - 23/33- 23/33-0.35 0.127 0.096 0.127 0.064 最后弯矩-5.35-10.7-9.3-2.442.190.254.12(e) 解：当D 发生单位转角时：()()2414-=⨯⨯=m EI K Y C 则()）假设12(441==⨯=-m EI EIM DC73,74,3716,379,371216,12,16,9,12=====∴=====∴EB ED DE DA DC DE EB DE DA DC S S S S S μμμμμ 结点D EB 杆端 DC DA DE ED EB BE 分配系数 12/37 9/37 16/37 4/7 3/7 固结 固端弯矩0 0 -9 9 0 0 分配传递-2.57 -5.14 -3.86 -1.93 3.75 2.81 5 -2.5 -0.72 -1.43 -1.07 -0.54 0.230.18 0.31 0.16 最后弯矩3.982.99-6.985-5-2.47(f) 解：截取对称结构为研究对象。

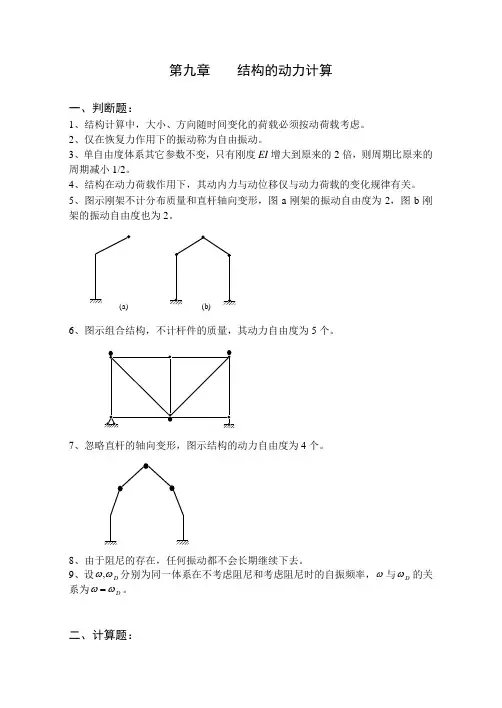
第九章 结构的动力计算一、判断题：1、结构计算中，大小、方向随时间变化的荷载必须按动荷载考虑。

2、仅在恢复力作用下的振动称为自由振动。

3、单自由度体系其它参数不变，只有刚度EI 增大到原来的2倍，则周期比原来的周期减小1/2。

4、结构在动力荷载作用下，其动内力与动位移仅与动力荷载的变化规律有关。

5、图示刚架不计分布质量和直杆轴向变形，图a 刚架的振动自由度为2，图b 刚架的振动自由度也为2。

6、图示组合结构，不计杆件的质量，其动力自由度为5个。

7、忽略直杆的轴向变形，图示结构的动力自由度为4个。

8、由于阻尼的存在，任何振动都不会长期继续下去。

9、设ωω,D 分别为同一体系在不考虑阻尼和考虑阻尼时的自振频率，ω与ωD 的关系为ωω=D 。

二、计算题：10、图示梁自重不计，求自振频率ω。

l l /411、图示梁自重不计，杆件无弯曲变形，弹性支座刚度为k ，求自振频率ω。

l /2l /212、求图示体系的自振频率ω。

l l0.5l 0.513、求图示体系的自振频率ω。

EI = 常数。

ll 0.514、求图示结构的自振频率ω。

l l15、求图示体系的自振频率ω。

EI =常数，杆长均为l 。

16、求图示体系的自振频率ω。

杆长均为l 。

17、求图示结构的自振频率和振型。

l /2l /2l /18、图示梁自重不计，W EI ==⨯⋅2002104kN kN m 2,，求自振圆频率ω。

B2m2m19、图示排架重量W 集中于横梁上，横梁EA =∞，求自振周期ω。

EIEIW20、图示刚架横梁∞=EI 且重量W 集中于横梁上。

求自振周期T 。

EIEIWEI 221、求图示体系的自振频率ω。

各杆EI = 常数。

a aa22、图示两种支承情况的梁，不计梁的自重。

求图a 与图b 的自振频率之比。

l /2l/2(a)l /2l /2(b)23、图示桁架在结点C 中有集中重量W ，各杆EA 相同，杆重不计。

求水平自振周期T 。

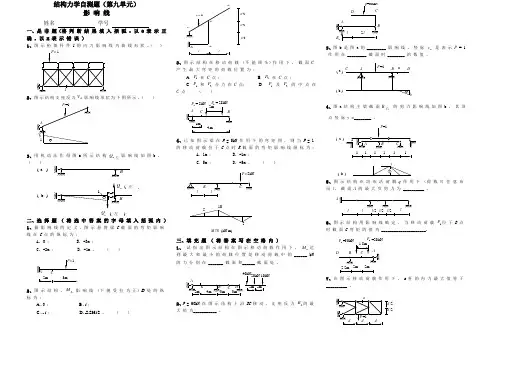
结构力学自测题（第九单元）影 响 线姓名 学号一、是 非 题（将 判 断 结 果 填 入 括 弧 ：以 O 表 示 正 确 ，以 X 表 示 错 误 ）1、图 示 桁 架 杆 件 1 的 内 力 影 响 线 为 曲 线 形 状 。

（ ）2、图 示 结 构 支 座 反 力 V A 影 响 线 形 状 为 下 图 所 示 。

（ ）3、用 机 动 法 作 得 图 a 所 示 结 构 Q B 左 影 响 线 如 图 b 。

（ ）( )ab( )B( 左 )Q B )二、选 择 题 （ 将 选 中 答 案 的 字 母 填 入 括 弧 内 ）1、据 影 响 线 的 定 义 ，图 示 悬 臂 梁 C 截 面 的 弯 矩 影 响线 在 C 点 的 纵 标 为 ：A. 0 ；B. -3m ；C. -2m ；D. -1m 。

（）2、图 示 结 构 ，M A 影 响 线 （下 侧 受 拉 为 正）D 处 的 纵标 为 ：A . 0 ；B . l ；C . - l ；D. -2.236l /2 。

（ ）ll22l/23、图 示 结 构 在 移 动 荷 载 （不 能 调 头）作 用 下 ， 截 面 C产 生 最 大 弯 矩 的 荷 载 位 置 为 ：A. P 1 在 C 点 ；B. P 2 在 C 点 ；C. P 1 和 P 2 合 力 在 C 点；D. P 1 及 P 2 的 中 点 在 C 点 . （ ）P 2= 28kN4、已 知 图 示 梁 在 P = 5kN 作 用 下 的 弯 矩 图 ， 则 当 P = 1的 移 动 荷 载 位 于 C 点 时 K 截 面 的 弯 矩 影 响 线 纵 标 为 ：A. 1m ；B. -1m ；C. 5m ；D. -5m 。

（ ）1055图 M (kN.m)三、填 充 题 （ 将 答 案 写 在 空 格 内 ）1、 试 指 出 图 示 结 构 在 图 示 移 动 荷 载 作 用 下 ， M K 达到 最 大 和 最 小 的 荷 载 位 置 是 移 动 荷 载 中 的 ______ kN 的 力 分 别 在 _______ 截 面 和______ 截 面 处 。

一．是非题（将判断结果填入括弧：以O 表示正确，X 表示错误）（本大题分4小题，共11分）1 . (本小题 3分)图示结构中DE 杆的轴力F NDE =F P /3。

（ ）.2 . (本小题 4分)用力法解超静定结构时，只能采用多余约束力作为基本未知量。

（ ）3 . (本小题 2分)力矩分配中的传递系数等于传递弯矩与分配弯矩之比，它与外因无关。

（ ）4 . (本小题 2分)用位移法解超静定结构时，基本结构超静定次数一定比原结构高。

（ ）二．选择题（将选中答案的字母填入括弧内）（本大题分5小题，共21分）1 （本小题6分）图示结构EI=常数，截面A 右侧的弯矩为：（ ） A ．2/M ； B ．M ； C ．0； D. )2/(EI M 。

22. （本小题4分）图示桁架下弦承载，下面画出的杆件内力影响线，此杆件是：（ ） Ａ.ch; B.ci; C.dj; D.cj.3. (本小题 4分)图a 结构的最后弯矩图为：A. 图b;B. 图c;C. 图d;D.都不对。

（ ）( a)(b) (c) (d)4. (本小题 4分)用图乘法求位移的必要条件之一是： A.单位荷载下的弯矩图为一直线； B.结构可分为等截面直杆段； C.所有杆件EI 为常数且相同； D.结构必须是静定的。

( ) 5. （本小题3分）=1图示梁A 点的竖向位移为（向下为正）：( )Ａ．F P l 3/(24EI); B. F P l 3/(!6EI); C. 5F P l 3/(96EI); D. 5F P l 3/(48EI).三（本大题 5分）对图示体系进行几何组成分析。

四（本大题 9分）图示结构B 支座下沉4 mm ，各杆EI=2.0×105 kN ·m 2，用力法计算并作M 图。

五（本大题 11分） 用力矩分配法计算图示结构，并作M 图。

EI=常数。

六（本大题14分）已知图示结构，422.110 kN m ,10 kN/m EI q =⨯⋅=求B 点的水平位移。

A B
C D
、单自由度体系在简谐荷载作用下，下列哪种情况内力与位移的动力系数相同？
A B
C D
、当简谐荷载作用于有阻尼的单自由度体系质点上时，若荷载频率远远大于体系的自振频率时，则此时与动荷载相平衡的主要是
A B
C D
、如果体系的阻尼增大，下列论述错误的是
A B
C D
、在低阻尼体系中不能忽略阻尼对什么的影响？
A B
C D
E、动力位移
2、单自由度体系的强迫振动主要计算
A、频率
B、周期
C、振型
D、动力内力
E、动力位移
3、具有弹性支座的梁，如要降低梁的自振频率ω，可采取下列那些措施？
A、增大质量
B、减小梁的刚度
C、减小弹性支座的刚度
D、增大荷载值
E、增大荷载频率
4、在低阻尼体系中可以忽略阻尼对什么的影响？
A、频率
B、周期
C、自由振动的振幅
D、主振型
E、共振区外的强迫振动的振幅
5、如果体系的阻尼数值减小，下列论述正确的是
A、动力系数变大
B、动力系数减小
C、自由振动的振幅衰减速度加快
D、自振周期减小
正确错误、连续分布质量体系是无限自由度体系。

正确错误、具有集中质量的体系，其动力计算自由度就等于其集中质量数。

正确错误β也称为动力放大系数，它总是大于
正确错误、在简谐振动情况下，质点的惯性力永远与质点位移同向。

正确错误。

9.1　复习笔记【知识框架】【重点难点归纳】一、力矩分配法（见表9-1-1）　★★★★图9-1-1二、无剪力分配法（见表9-1-2）　★★表9-1-2　无剪力分配法表9-1-3　剪力分配法9.2　课后习题详解复习思考题1．什么是转动刚度？什么是分配系数？为什么一刚结点处各杆端的分配系数之和等于1？答：（1）转动刚度的定义杆端的转动刚度是指当杆件的近端转动单位角时，在该近端产生的弯矩。

（2）分配系数的定义分配系数是指结点某一杆端的劲度系数与该结点处所有杆端的劲度系数的比值。

（3）刚结点处各杆端的分配系数之和等于1的原因：因为分配系数的计算公式，在刚节点处各杆端分配系数之和应为1ijij n ijj S Sμ==∑111n ij j ij n ijj SSμ====∑∑2．单跨超静定梁的劲度系数和传递系数与杆件的线刚度有何关系？答：单跨超静定梁的劲度系数不仅与杆件线刚度i＝EI/l相关，而且与杆件另一端（又称远端）的支承情况有关；传递系数与杆件的线刚度无关，只与远端支承形式有关。

3．图9-2-1所示三个单跨梁，仅B端约束不同。

它们的劲度系数S AB和传递系数C AB 是否相同，为什么？图9-2-1答：不考虑杆件轴向变形，（a）、（b）、（c）三个单跨梁的劲度系数均相同，即S AB＝4i，其中i为杆件的线刚度；（a）、（b）、（c）三个图的传递系数均相同，即C AB＝0.5。

因为虽然B端约束表面上形式各异，但在不考虑杆件轴向变形的条件下，（a）、（b）、（c）三个单跨梁在B端的最终约束效果上均可以当成固定端来处理。

若考虑杆件轴向变形，（a）、（c）的劲度系数相同，（b）远端可在水平向自由收缩，A端转到相同的转角需要的力更小，因此劲度系数略小于（a）、（c）。

4．什么是不平衡力矩？如何计算不平衡力矩？为什么要将它反号才能进行分配？答：（1）不平衡力矩的定义不平衡力矩是指在附加约束结点处各固端弯矩所不能平衡的差额。

9-7试求图示等截面单跨梁的极限荷载。

梁的截面为矩形b ×h=5 cm×20 cm,s σ=235 Mpa 。

解 根据弯矩图形状，很容易判断，形成机构说，塑性铰出现在B 、D 两点，故()Pu u u 22u e Pu 11335cm 20cm 235MPa 4704kN F l M M M bh F l l l lσ-=⨯⨯====习题9-7图9-8试求图示等截面单跨梁的极限荷载。

解：梁变成机构时，任意截面的弯矩为3u23u u 11()66d ()110d 6231166M x qlx qx M l M x ql qx x x l M ql q M q l =--=-===--=9-9试求图示等截面超静定梁的极限荷载。

解： 第一跨变成机构时，()()11Pu u Pu u 181.56m 2(kN)49F M F M ⨯⨯==第二跨变成机构时，()()22Pu u Pu u 16m 1.5(kN)4F M F M ⨯⨯==极限弯矩为()2Pu Pu u (kN)F F M ==习题9-8图9-10试求图示等截面连续梁的极限弯矩。

解： 第一跨变成机构时，()211u u 1320kN/m 6m 60kNm 82M M ⨯⨯==()()()()()()()()()()2u11u u 211111u u u uu 1122u u 212u 11()22d ()1110d 221111112222211822361.92kNm 2xM x qlx qx M lM M x ql qx M x l x l qlM M M M ql l q l l M ql ql l ql M M ql ql M ql =--=--==-⎛⎫⎛⎫⎛⎫=----- ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭=-+-== 第二跨变成机构时，()()()222u u 1120kN/m 6m 40kN 6m 275kNm 84M M ⨯⨯+⨯⨯==第三跨变成机构时，()()33u u 1332080kN 8m kNm 106.7kNm 423M M ⨯⨯=== 极限弯矩为()3u u 106.7kNm M M ==9-11试求图示阶形柱的极限荷载。

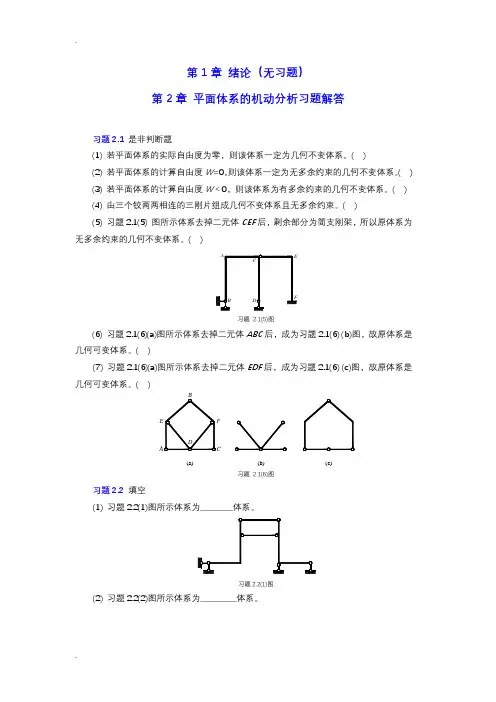
结构力学课后习题答案(总23页)--本页仅作为文档封面，使用时请直接删除即可----内页可以根据需求调整合适字体及大小--习题及参考答案【习题2】【习题3】【习题4】【习题5】【习题6】【习题8】【习题9】【习题10】【习题11】【习题12】【习题13】【习题14】【参考答案】习题22-1～2-14试对图示体系进行几何组成分析，如果是具有多余联系的几何不变体系，则应指出多余联系的数目。

题2-1图题2-2图题2-3图题2-4图题2-5图题2-6图题2-7图题2-8图题2-9图题2-10图题2-11图题2-12图 题2-13图 题2-14图习题33-1 试作图示多跨静定梁的M 及Q 图。

(b)(a)20kN10kN40kN20kN/m40kN题3-1图3-2 试不计算反力而绘出梁的M 图。

(b)5kN/m40kN(a)题3-2图习题44-1 作图示刚架的M 、Q 、N 图。

(c)(b)(a)/20kN /m2kN /m题4-1图4-2 作图示刚架的M 图。

P(e)(d)(a)(b)(c)20k N /m4kN题4-2图4-3 作图示三铰刚架的M 图。

(b)(a)题4-3图4-4 作图示刚架的M 图。

(a)题4-4图4-5 已知结构的M 图，试绘出荷载。

(b)(a)题4-5图4-6 检查下列刚架的M 图，并予以改正。

(e)(g)(h)P(d)(c)(a)(b)(f)题4-6图习题55-1 图示抛物线三铰拱轴线方程x x l lfy )(42-=，试求D 截面的内力。

题5-1图5-2 带拉杆拱，拱轴线方程x x l lf y )(42-=，求截面K 的弯矩。

C题5-2图 题5-3图5-3 试求图示带拉杆的半圆三铰拱截面K 的内力。

习题66-1 判定图示桁架中的零杆。

(c)(b)题6-1图6-2 用结点法计算图示桁架中各杆内力。

(b)题6-2 图6-3 用截面法计算图示桁架中指定各杆的内力。

(b)题6-3图6-4 试求图示组合结构中各链杆的轴力并作受弯杆件的M 、Q 图。

第9章平面体系的几何组成分析习题.【解】若上部结构与地基之间的连接比较多（N4）,能够考虑先将上部结构中的某•刚片与地基连成一个大刚片。

然后，在考虑这个大刚片与上部其它杆件的连接。

本例中，上部结构与地基之间用4个约束连接。

杆件ABE与地基之间用钗A和一根不同过该絞的链杆B相连，组成几何不变体系，且没有多余约束。

所以，能够将杆件ABE与地基看成一个没有多余约束的大刚片。

杆件FCD用三根既不相互平行又不相交于一点的链杆（链杆EF、链杆C、链杆D）与这个大刚片相连，组成一个更大的几何不变体系，且没有多余约束。

杆件ABE与地基之间用平行链杆A和一根不同过该絞的链杆B相连，组成几何不变体系，且没有多余约束。

将杆件ABE与地基看成一个没有多余约束的大刚片。

杆件FCD用三根既不相互平行又不相交于一点的链杆（链杆EF、链杆C、链杆D）与这个大刚片相连，组成一个更大的几何不变体系，且没有多余约束。

-I*羡诊为习题（C）图若上部结构中有皎接三角形，能够考虑将这些三角形看成刚片，然后在进行分析。

刚片I与地基组成•个没有多余约束的大刚片。

这个大刚片与刚片II用三根既不相互平行又不相交于一点的链杆相连，组成一个更大的几何不变体系，且没有多余约束。

习题（d）图将扩大的三角形看成刚片。

先分析一部分：左边的刚片与地基组成一个大刚片ABCD。

增加二元体：在大刚片ABCD上增加二元体DE杆和链杆E,组成一个更大的刚片。

此刚片与刚片GH1F由三根延长线交于H点的链杆（杆件CG、杆件FE、链杆1）相连。

故，体系为瞬变体系。

若上部结构与地基之间用三个约束连接，且符合几何不变体系的组成规律，能够只分析上部结构。

上部结构的分析结论就是整个体系的分析结论。

若折杆只用两个较与其它物体相连，能够将折杆看成是连接两个钗的直杆。

去掉二元体。

剩下部分为两个刚片用两个钗连接，为几何不变体系,且有一个多余约束。

故，整体体系也为几何不变体系，且有一个多余约束。

1、清华5-6 试用力矩分配法计算图示连续梁，并画其弯矩图和剪力图。

C清华V图M(kN解：（1）计算分配系数：320.632440.4324BABABA BCBCBCBA BCs is s i is is s i iμμ⨯===+⨯+⨯⨯===+⨯+⨯（2）计算固端弯矩：固端弯矩仅由非结点荷载产生，结点外力偶不引起固端弯矩，结点外力偶逆时针为正直接进行分配。

3360667.51616FABFBAMPlM=⨯⨯===⋅kN m（3）分配与传递，计算列如表格。

（4）叠加固端弯矩和分配弯矩或传递弯矩，得各杆端的最后弯矩，作弯矩图如图所示。

（5）根据弯矩图作剪力图如图所示。

0153027.60153032.63517.58.756AB BA AB AB AB BA BA BA BC CB BC CB M M V V l M M V V l M M V V l ++=-=-=++=-=--=+--==-=-=5kN 5kN kN2、利用力矩分配法计算连续梁，并画其弯矩图和剪力图。

4m1m2m2m原结构简化结构·解：（1）计算分配系数：,4,34BA BC BA BC EIi i i S i S i =====令 430.4290.5714343BC BA BA BC BA BC BA BC s s iis s i is s i iμμ======++++（2）计算固端弯矩：CD 杆段剪力和弯矩是静定的，利用截面法将外伸段从C 处切开，让剪力直接通过支承链杆传给地基，而弯矩暴露成为BC 段的外力偶矩，将在远端引起B 、C 固端弯矩。

22204101088154102020828F FAB BA F F BCCB Pl M M ql m M M ⨯=-=-=-⋅⋅⨯=-+=-+=-⋅=⋅kN m,=kN m kN m,kN m（3）分配与传递，计算列如表格。

（4）叠加固端弯矩和分配弯矩或传递弯矩，得各杆端的最后弯矩，作弯矩图如图所示。

第三章 静定结构的位移计算一、判断题：1、虚位移原理等价于变形谐调条件，可用于求体系的位移。

2、按虚力原理所建立的虚功方程等价于几何方程。

3、在非荷载因素(支座移动、温度变化、材料收缩等)作用下，静定结构不产生内力，但会有位移且位移只与杆件相对刚度有关。

4、求图示梁铰C 左侧截面的转角时，其虚拟状态应取：A.;; B.D.C.M =15、功的互等、位移互等、反力互等和位移反力互等的四个定理仅适用于线性变形体系。

6、已知M p 、M k 图，用图乘法求位移的结果为：()/()ωω1122y y EI +。

M k M p7、图a 、b 两种状态中，粱的转角ϕ与竖向位移δ间的关系为：δ=ϕ 。

8、图示桁架各杆E A 相同，结点A 和结点B 的竖向位移均为零。

9、图示桁架各杆EA =常数，由于荷载P 是反对称性质的，故结点B 的竖向位移等于零。

二、计算题：10、求图示结构铰A 两侧截面的相对转角ϕA ，EI = 常数。

q l l l /211、求图示静定梁D 端的竖向位移∆DV 。

EI = 常数，a = 2m 。

a a a 10kN/m12、求图示结构E 点的竖向位移。

EI = 常数。

l l l /3/3q13、图示结构，EI=常数，M =⋅90kN m , P = 30kN 。

求D 点的竖向位移。

P 3m 3m 3m14、求图示刚架B 端的竖向位移。

ql15、求图示刚架结点C 的转角和水平位移，EI = 常数。

16、求图示刚架中Ｄ点的竖向位移。

EI＝常数。

l/217、求图示刚架横梁中Ｄ点的竖向位移。

EI ＝常数。

18、求图示刚架中D 点的竖向位移。

E I = 常数 。

ql l/219、求图示结构Ａ、Ｂ两截面的相对转角，EI ＝常数。

l/23l/320、求图示结构A 、B 两点的相对水平位移，E I = 常数。

l l21、求图示结构B 点的竖向位移，EI =常数。

l l22、图示结构充满水后，求A 、B 两点的相对水平位移。

第9章超静定结构的实用计算方法与概念分析习题答案9-1 试说出何为杆端转动刚度、弯矩分配系数和传递系数，为什么弯矩分配法一般只能用于无结点线位移的梁和刚架计算。

9-2 试用弯矩分配法计算图示梁和刚架，作出M 图，并求刚结点B 的转角φB 。

解：设EI=6，则5.1,1==BC AB i i53.05.13145.1347.05.131414=⨯+⨯⨯==⨯+⨯⨯=BCBA μμ结点 A BC 杆端 AB BA BC 分配系数 固端 0.47 0.53 绞支 固端弯矩 -60 60 -30 0 分配传递 -7.05 -14.1 -15.9 0 最后弯矩-67.0545.9-45.9()()()逆时针方向215.216005.6721609.4522131m KN EIEI m M m M i AB AB BA BA B ⋅-=⎥⎦⎤⎢⎣⎡+---=⎥⎦⎤⎢⎣⎡---=θ(b)解：设EI=9，则3,31,1====BE BD BC AB i i i i6m3m 3m2m6m2m12.0141333331316.0141333331436.01413333333=⨯+⨯+⨯+⨯⨯==⨯+⨯+⨯+⨯⨯==⨯+⨯+⨯+⨯⨯==BC BA BE BD μμμμ结点 A BC 杆端 AB BA BC BD BE 分配系数 固端 0.16 0.12 0.36 0.36 绞支 固端弯矩 0 0 0 45 -90 0 分配传递 3.6 7.2 5.4 16.2 16.2 0 最后弯矩3.67.25.461.2-73.8()()()顺时针方向22.1606.32102.732131m KN EIEI m M m M i AB AB BA BA B ⋅=⎥⎦⎤⎢⎣⎡---=⎥⎦⎤⎢⎣⎡---=θ9-3 试用弯矩分配法计算图示刚架，并作出M 图。

(a)解：Ｂ为角位移节点设EI=8,则1==BC AB i i ，5.0==BC BA μμ 固端弯矩()m KN l b l Pab M BA ⋅=⨯⨯⨯⨯=+=4882124432222 m KN l M BC ⋅-=⋅+-=582621892 结点力偶直接分配时不变号结点 A BC 杆端 AB BA BC 分配系数 铰接 0.5 0.5 固端弯矩 0 48 -58 12 分配传递50 50 55124m 4m8m2m最后弯矩 0103 -3 12(b)解：存在B 、C 角位移结点 设EI=6，则1===CD BC AB i i i 73741413145.0141414==⨯+⨯⨯==⨯+⨯⨯==BC CB BC BA μμμμ固端弯矩： mKN M M M m KN M m KN M CDCB BC BA AB ⋅-=⨯+⨯-===⋅-=⋅-=14021808640080802结点 A BC杆端 AB BA BC CB CD 分配系数 固结 0.5 0.5 4/7 3/7 固端弯矩-80 80 0 0 -140 分配传递-20 -40 -40 -20 47.5 91.4 68.6 -11.4 -22.8 -22.8 -11.4 3.25 6.5 4.9 -0.82-1.63-1.63-0.820.6 0.45 最后弯矩-112.2215.57-15.4866.28-66.052m 6m2m2m2m 6m(c)解：B 、C 为角位移结点51411,5441454414,51411=+==+==+==+=CD CBBC BA μμμμ固端弯矩：mKN M mKN M mKN M mKN M mKN M mKN M DC CD CB BC BA AB ⋅-=⨯-=⋅-=⨯-=⋅=⨯=⋅-=⨯-=⋅=⨯=⋅=⨯=10065242003524501252450125241283424646424222222结点 A BCD 杆端 AB BA BC CB CD 滑动 分配系数 滑动 0.2 0.8 0.8 0.2 -100固端弯矩64 128 -50 50 -200 分配传递15.6 -15.6 -62.4 -31.272.48 144.96 36.24 -36.24 14.5 -14.5 -58 -29 11.6 23.2 5.8 -5.8 2.32-2.32-9.28-4.643.7 0.93 -0.93 最后弯矩96.4295.58-95.6157.02-157.03-142.974m5m5m3m96.42(d) 解：11313141413114131414145.0141414=⨯+⨯+⨯⨯===⨯+⨯+⨯⨯===⨯+⨯⨯=DBDE DC CD CA μμμμμ 固端弯矩：mKN M mKN M ED DE ⋅=⋅-=⨯-=383812422结点 A CD E 杆端 AC CA CD DC DB DE ED 分配系数 固结 0.5 0.5 4/11 3/11 4/11 固结固端弯矩0 0 0 0 0 -2.67 2.67 分配传递-5-10 -10 -546/33 92/33 69/33 92/33 46/33 -0.35 - 23/33- 23/33-0.350.127 0.096 0.127 0.064 最后弯矩-5.35-10.7-9.3-2.442.190.254.12(e)4m6m4m4m4m解：当D 发生单位转角时：()()2414-=⨯⨯=m EI K Y C 则()）假设12(441==⨯=-m EI EIM DC73,74,3716,379,371216,12,16,9,12=====∴=====∴EB ED DE DA DC DE EB DE DA DC S S S S S μμμμμ 结点 D EB 杆端 DC DA DE ED EB BE 分配系数 12/37 9/37 16/37 4/7 3/7 固结 固端弯矩0 0 -9 9 0 0 分配传递-2.57 -5.14 -3.86 -1.93 3.75 2.81 5 -2.5 -0.72 -1.43 -1.07 -0.54 0.230.18 0.31 0.16 最后弯矩3.982.99-6.985-5-2.47(f)解：截取对称结构为研究对象。