微电机临界转速计算方法

转轴的挠度及临界转速计算程序(一具有集中载荷的两支点轴承的计算(如图2-118转轴重量: Q=285(kg L1=49转子重量: G1=365(kg L2=52.1铁心有效长度:L fe=46(cm L=126转子外径: D1=37.2(cm La=36单边气隙: δ=0.4(cm G2=20弹性模量: E= 2.06E+06(MPay=0.388888889气隙磁密: Bδ=5781GS z=0.285714286同步转速: n=5000r/min根据y、z值查图2-119功率: P=300kWθ=0.5过载系数: K= 2.25b处轴径212、挠度系数计算:单位:cm cm4cm cm3cm3轴a~b段d i J i X i Xi 3Xi3-X(i-1319321.89906251533753375 210490.62522.511390.638015.625 311718.324062526.518609.637219 4121017.3633.537595.3818985.75 5131401.27406342.576765.6339170.25 6141884.78547.5107171.930406.25 7000008000009000001000000∑ K ab=轴c~b段d i J i X i Xi 3Xi3-X(i-1318200.96 4.591.12591.125 29321.89906259.5857.375766.25311718.324062518.56331.6255474.25 4131401.27406327.520796.8814465.25 5141884.78532.534328.1313531.25 600000 700000 800000 900000 1000000∑ K cb=3、轴在b点的柔度:αbb= 3.44022E-06cm/kg一、绕度及临界转速计算4、磁拉力刚度:K0=8753.301622kg/cm5、初始单边磁拉力:P0=350.1320649kg6、由G1重量引起的b点绕度:f1=0.001875367cm7、滑环重量G2引起的b点绕度:f2=7.67363E-05cm8、单边磁拉力引起的b点绕度:fδ=0.001883694cm9、轴在b点的总绕度:f=0.003835798cm应小于异步电机同步电机10、转轴临界转速:n kp=6635.556016rpm二、轴的强度计算:1、最大转矩:Mmax=1289.25N.m2、bb点处的弯矩:Mbb=1419.958282N.m3、bb处的交变弯矩应力:ζbb=1533266.691N/m24、bb处的剪切应力:ηbb=696064.1399N/m2ηn=348032.07N/m2脉动循环下的剪切应力:η∞=870080.1749N/m25、轴在bb处受到的总负荷应力:ζ= 2.319281093N/mm2应该小于材料许用[ζ]=三、轴承计算:1、转子所受最大径向力:W=715.1320649kg2、a处轴承支承力:Pa=295.7014332kg3、c处轴承支承力:Pc=278.1069141kg4、轴承寿命:Lh=35986600.69小时应大于10^5式中:ε=3.33f t=1载荷系数F f=1.1温度系数c=39600轴承额定动负荷P i=278.11当量动负荷(二带外伸端的两支点轴承的计算(如图2-120一、基本参数:电枢重量(G1包括转轴中部重量的2/3和滑环的重量在内一、绕度及临界转速计算2、柔度系数计算:3、轴的柔度:α11=7.56093E-07cm/kgα22= 2.42497E-06cm/kgα12=-8.91046E-07cm/kgα21=-8.91046E-07cm/kg4、转子重量所引起的挠度:b处:f1'=0.006714438cmd处:f2'=-0.006606742cm5、磁拉力刚度:转子一:K1=136812.9233kg/cm转子二:K2=0kg/cm6、初始磁拉力:P1=1368.129233kgP2=0kg7、由磁拉力引起的挠度:F0= 1.03954E-12E0=0.896556679b处:f1"=0.001153785cmd处:f2"=-0.001359721cm8、总挠度:同步机b处:f1=0.007868222cm应该<0.008d处:f2=-0.007966462cm应该<0 9、临界转速:一次:n k=3506.387398rpm应该>975 速计算程序(如图2-118(cm(cm(cm(cm(kg曲线cmcm-1[X i3-X(i-13]/J i10.4846530916.3375796210.0497816718.6617814727.9533112416.1324766599.61958374[X i3-X(i-13]/J i0.4534484472.3804045727.62086401610.32292717.17920081127.956844950.04cm0.032cm55N/mm2小时图2-120(cm(cm(cm(cmMpa[X i3-X(i-13]/J i X i2X i2-X(i-12[X i2-X(i-12]/J i X i-X i-1(X i-X i-1/J i0.918664587-0.3518347250.3368560430.903685905[X i3-X(i-13]/J i X i2X i2-X(i-12[X i2-X(i-12]/J i X i-X i-1(X i-X i-1/J i 0.056840583204204.490.00397486614.30.00027796311.2813244395459340.80.1133507583.40.00101206-0.5198816461089-8456.29-0.004903061-64.7-3.75139E-0500-10890-330000000000000000000000000异步机cm应该<0.01cm cm应该<0cm rpm满足要求。

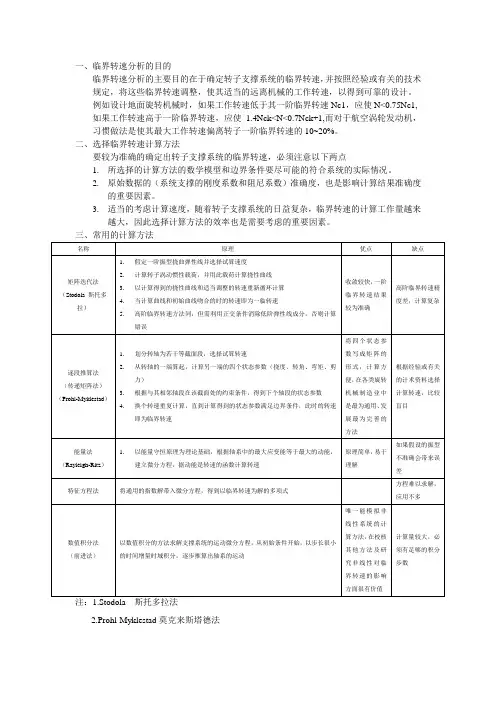
一、临界转速分析的目的临界转速分析的主要目的在于确定转子支撑系统的临界转速，并按照经验或有关的技术规定，将这些临界转速调整，使其适当的远离机械的工作转速，以得到可靠的设计。

例如设计地面旋转机械时，如果工作转速低于其一阶临界转速Nc1，应使N<0.75Nc1, 如果工作转速高于一阶临界转速，应使 1.4Nck<N<0.7Nck+1,而对于航空涡轮发动机，习惯做法是使其最大工作转速偏离转子一阶临界转速的10~20%。

二、选择临界转速计算方法要较为准确的确定出转子支撑系统的临界转速，必须注意以下两点1.所选择的计算方法的数学模型和边界条件要尽可能的符合系统的实际情况。

2.原始数据的（系统支撑的刚度系数和阻尼系数）准确度，也是影响计算结果准确度的重要因素。

3.适当的考虑计算速度，随着转子支撑系统的日益复杂，临界转速的计算工作量越来越大，因此选择计算方法的效率也是需要考虑的重要因素。

三、常用的计算方法2.Prohl-Myklestad莫克来斯塔德法传递矩阵法基本原理：传递矩阵法的基本原理是，去不同的转速值，从转子支撑系统的一端开始，循环进行各轴段截面状态参数的逐段推算，直到满足另一端的边界条件。

优点：对于多支撑多元盘的转子系统，通过其特征值问题或通过建立运动微分方程的方法求解系统的临界转速和不平衡响应，矩阵的维数随着系统的自由度的增加而增加，计算量往往较大：采用传递矩阵法的优点是矩阵的维数不随系统的自由度的增加而增大，且各阶临界转速计算方法相同，便于程序实现，所需存储单元少，这就使得传递矩阵法成为解决转子动力学问题的一个快速而有效的方法。

缺点：求解高速大型转子的动力学问题时，有可能出现数值不稳定现象。

今年来提出的Riccati 传递矩阵法，保留传递矩阵的所有优点，而且在数值上比较稳定，计算精度高，是一种比较理想的方法，但目前还没有普遍推广。

轴段划分：首先根据支撑系统中刚性支撑（轴承）的个数划分跨度。

临界转速的计算WEIHUA system office room 【WEIHUA 16H-WEIHUA WEIHUA8Q8-一、临界转速分析的目的临界转速分析的主要目的在于确定转子支撑系统的临界转速，并按照经验或有关的技术规定，将这些临界转速调整，使其适当的远离机械的工作转速，以得到可靠的设计。

例如设计地面旋转机械时，如果工作转速低于其一阶临界转速Nc1，应使N<,如果工作转速高于一阶临界转速，应使<N<+1,而对于航空涡轮发动机，习惯做法是使其最大工作转速偏离转子一阶临界转速的10~20%。

二、选择临界转速计算方法要较为准确的确定出转子支撑系统的临界转速，必须注意以下两点1.所选择的计算方法的数学模型和边界条件要尽可能的符合系统的实际情况。

2.原始数据的（系统支撑的刚度系数和阻尼系数）准确度，也是影响计算结果准确度的重要因素。

3.适当的考虑计算速度，随着转子支撑系统的日益复杂，临界转速的计算工作量越来越大，因此选择计算方法的效率也是需要考虑的重要因素。

三、常用的计算方法应用不多数值积分法（前进法）以数值积分的方法求解支撑系统的运动微分方程，从初始条件开始，以步长很小的时间增量时域积分，逐步推算出轴系的运动唯一能模拟非线性系统的计算方法，在校核其他方法及研究非线性对临界转速的影响方面很有价值计算量较大，必须有足够的积分步数注：斯托多拉法莫克来斯塔德法传递矩阵法基本原理：传递矩阵法的基本原理是，去不同的转速值，从转子支撑系统的一端开始，循环进行各轴段截面状态参数的逐段推算，直到满足另一端的边界条件。

优点：对于多支撑多元盘的转子系统，通过其特征值问题或通过建立运动微分方程的方法求解系统的临界转速和不平衡响应，矩阵的维数随着系统的自由度的增加而增加，计算量往往较大：采用传递矩阵法的优点是矩阵的维数不随系统的自由度的增加而增大，且各阶临界转速计算方法相同，便于程序实现，所需存储单元少，这就使得传递矩阵法成为解决转子动力学问题的一个快速而有效的方法。

电机转轴的挠度及临界转速计算在电机转轴设计中，挠度的计算有多种方法，其中最常用的方法是应用力学原理，根据受力和几何特性进行分析。

以下将介绍两种常见的计算电机转轴挠度的方法。

1.等效转子法：在这种方法中，电机转轴可以看作是由一系列均匀分布的质点组成的等效转子。

对于每个质点，计算它受到的外力和转轴支承力的合力。

根据力的平衡条件，可以得到转轴的弯曲方程。

最终，通过求解这个方程，可以得到转轴挠度随位置的变化情况。

2.梁弯曲方程法：在这种方法中，电机转轴可以看作是一根梁，在受到外力作用时产生的弯曲可以通过梁弯曲方程进行计算。

这个方程描述了弯曲曲线在不同位置的形状以及弯曲程度。

通过求解这个方程，可以得到转轴不同位置处的挠度情况。

在实际应用中，可以根据电机的设计需求和具体情况选择适合的挠度计算方法。

并且，为了保证电机的安全运行，还需要计算转轴的临界转速。

临界转速是指在这个转速下，电机转轴可能发生共振或破坏。

共振是指在一些特定频率下，电机转轴的挠度达到最大值，导致电机出现振动和摆动现象。

当电机的旋转频率接近共振频率时，共振现象可能会导致电机的破坏。

因此，计算电机转轴的临界转速是非常重要的。

计算电机转轴的临界转速可以采用有限元方法或模态分析方法。

有限元方法是一种基于数值计算的方法，可以模拟电机转轴在不同转速下的振动特性。

模态分析方法是一种通过求解电机转轴的振动模态方程，得到转轴的临界转速。

这两种方法可以同时考虑电机转轴的结构特性和弯曲特性，并给出最大转速值。

综上所述，电机转轴的挠度及临界转速是电机设计和运行过程中需要重点考虑的参数。

通过适用的计算方法，可以得到电机转轴在不同工况条件下的挠度情况和临界转速值，从而为电机的设计和运行提供重要依据。

临界转速计算公式
临界转速是指转子旋转时达到的最高转速，超过此转速会引起转
子失稳和振动，对运行安全和设备寿命产生威胁。

因此，正确计算临
界转速具有重要意义。

临界转速计算公式是通过分析转子结构和材料特性，综合考虑离
心力和刚度等因素得出的。

一般采用下列公式计算：
n_c = K * sqrt((E*I)/(m*L^3))
其中，n_c为临界转速，K为常数，E为转子材料的弹性模量，I
为转子截面惯性矩，m为转子质量，L为转子长度。

在计算时，需对转子结构和材料特性进行详细分析，确定K值，
计算出转子质量和长度，以及转子截面惯性矩等参数，进行代入计算。

临界转速计算是提高转子转速性能和安全性的重要手段。

对于已
经运行的设备，可以通过计算临界转速来查看其安全性，确定转速上
限并采取相应措施。

对于新设计的设备，临界转速计算则是制定设计
方案的重要依据之一。

此外，对于不同类型的转子，其临界转速计算
方法也有所不同，需根据具体情况确定计算公式和参数。

综上所述，临界转速计算是机械工程师必备的技能之一，对于提
高设备运行性能和延长寿命具有重要意义。

在实际工作中，需结合工
程实际，综合考虑各种因素，确定准确的临界转速，并采取相应措施，保障设备安全和稳定运行。

临界转速的计算修订稿
一、引言
临界转速是指其中一圆柱形转子运动时，其转动状态过渡由持续的稳定状态转步入波动态状态的转速，即临界转速，一般而言，转子若转速超过临界转速，则可能出现振动现象，导致机械电子设备受损甚至损坏，因此计算临界转速对确保转子的正常运行产生重要的意义。

二、传统的临界转速计算方法
传统计算临界转速的方法已经极为复杂，尤其当轴系存在多重不对称结构时，如波纹管、凸轮轴以及一些特殊构件时，传统方法更加困难，其基本原理是使用临界情况的方程，将不对称的形状因素考虑进去，然后求解出临界转速，使用这种方法计算非常复杂，耗时长，而且很难得到准确的结果。

三、基于物理模型的临界转速计算方法
因此，为了解决这个问题，研究者提出了基于物理模型的临界转速计算方法。

该方法结合了轴系结构的实验数据以及转子的物理模型，利用数值分析技术构建出了转动结构的动力学模型，并利用结构的模态参数和影响转子运动的质量参数计算得出了临界转速。

基于物理模型的临界转速计算方法的优点是，能够在较短的时间内得出准确的计算结果，相比传统方法，准确性更高。

临界转速的计算一、临界转速分析的目的临界转速分析的主要目的在于确定转子支撑系统的临界转速，并按照经验或有关的技术规定，将这些临界转速调整，使其适当的远离机械的工作转速，以得到可靠的设计。

例如设计地面旋转机械时，如果工作转速低于其一阶临界转速Nc1，应使N<0.75Nc1, 如果工作转速高于一阶临界转速，应使1.4Nck<n<0.7nck+1,而对于航空涡轮发动机，习惯做法是使其最大工作转速偏离转子一阶临界转速的10~20%。

< p="">二、选择临界转速计算方法要较为准确的确定出转子支撑系统的临界转速，必须注意以下两点1.所选择的计算方法的数学模型和边界条件要尽可能的符合系统的实际情况。

2.原始数据的（系统支撑的刚度系数和阻尼系数）准确度，也是影响计算结果准确度的重要因素。

3.适当的考虑计算速度，随着转子支撑系统的日益复杂，临界转速的计算工作量越来越大，因此选择计算方法的效率也是需要考虑的重要因素。

三、常用的计算方法名称原理优点缺点矩阵迭代法（Stodola 斯托多拉）1.假定一阶振型挠曲弹性线并选择试算速度2.计算转子涡动惯性载荷，并用此载荷计算挠性曲线3.以计算得到的挠性曲线和适当调整的转速重新循环计算4.当计算曲线和初始曲线吻合的时的转速即为一临转速5.高阶临界转速方法同，但需利用正交条件消除低阶弹性线成分，否则计算错误收敛较快，一阶临界转速结果较为准确高阶临界转速精度差，计算复杂逐段推算法（传递矩阵法）（Prohl-Myklestad）1.划分转轴为若干等截面段，选择试算转速2.从转轴的一端算起，计算另一端的四个状态参数（挠度、转角、弯矩、剪力）3.根据与其相邻轴段在该截面处的约束条件，得到下个轴段的状态参数4.换个转速重复计算，直到计算得到的状态参数满足边界条件，此时的转速即为临界转速将四个状态参数写成矩阵的形式，计算方便，在各类旋转机械制造业中是最为通用、发展最为完善的方法根据经验或有关的计术资料选择计算转速，比较盲目能量法（Rayleigh-Ritz）1.以能量守恒原理为理论基础，根据轴系中的最大应变能等于最大的动能，建立微分方程，据动能是转速的函数计算转速原理简单，易于理解如果假设的振型不准确会带来误差特征方程法将通用的指数解带入微分方程，得到以临界转速为解的多项式方程难以求解，应用不多数值积分法（前进法）以数值积分的方法求解支撑系统的运动微分方程，从初始条件开始，以步长很小的时间增量时域积分，逐步推算出轴系的运动唯一能模拟非线性系统的计算方法，在校核其他方法及研究非线性对临界转速的影响方面很有价值计算量较大，必须有足够的积分步数注：1.Stodola 斯托多拉法2.Prohl-Myklestad莫克来斯塔德法</n<0.7nck+1,而对于航空涡轮发动机，习惯做法是使其最大工作转速偏离转子一阶临界转速的10~20%。

申请上海交通大学工程硕士专业学位论文临界转速计算及其在电动机 转子设计中的应用学 校： 上海交通大学院 系：电子信息与电气工程学院班 级：Z0703121学 号：1070312017工程硕士生：徐俊工程领域：电气工程导 师Ⅰ：赵继敏（副教授）导 师Ⅱ：张学斌（高级工程师）上海交通大学电子信息与电气工程学院2010年4月A Dissertation Submitted to Shanghai Jiao Tong Universityfor Master Degree of EngineeringTHE CALCULATION OF CRITICAL SPEED AND APPLICATION IN DESIGNING ROTOR OF ELECTRIC MOTORAuthor：XU JUNSpecialty: Electrical EngineeringAdvisor Ⅰ: Prof. ZHAO JIMINAdvisor Ⅱ: Prof. ZHANG XUEBINSchool of Electronics and Electric EngineeringShanghai Jiao Tong UniversityShanghai, P.R.ChinaApril 18, 2010临界转速计算及其在电动机转子设计中的应用摘要随着工业的发展，人们对减少噪声污染提出了越来越高的要求，对降低噪声的要求日益强烈。

而电动机的振动是造成电动机噪声的主要原因之一，并且电动机振动给电机—负载系统的安全可靠运行也会带来很大的危害。

研究和控制电动机的振动和噪声问题，已成为国内外电机制造企业生存和发展的重要课题。

要减小电动机振动和噪声就必须认真研究电动机定转子的固有频率、固有模态等机械振动的特性，以便提出合理的结构设计。

电动机运行时如果转速在临界转速附近，电动机将产生严重的共振现象。

共振会导致轴或轴上零件甚至整个机械系统遭到破坏。

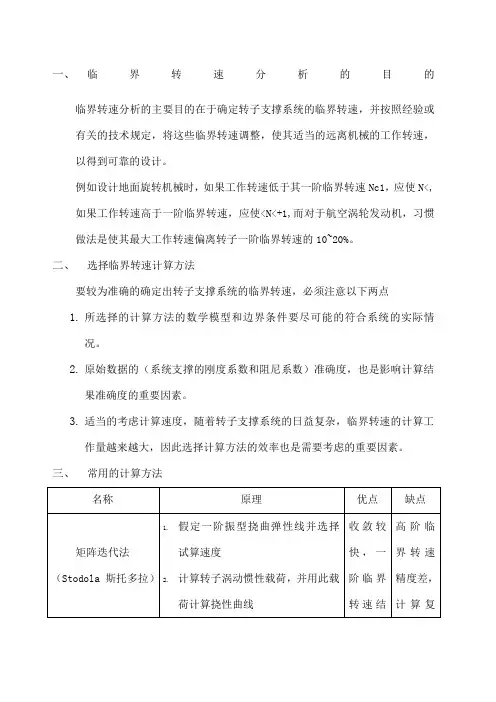
一、临界转速分析的目的临界转速分析的主要目的在于确定转子支撑系统的临界转速，并按照经验或有关的技术规定，将这些临界转速调整，使其适当的远离机械的工作转速，以得到可靠的设计。

例如设计地面旋转机械时，如果工作转速低于其一阶临界转速Nc1，应使N<,如果工作转速高于一阶临界转速，应使<N<+1,而对于航空涡轮发动机，习惯做法是使其最大工作转速偏离转子一阶临界转速的10~20%。

二、选择临界转速计算方法要较为准确的确定出转子支撑系统的临界转速，必须注意以下两点1.所选择的计算方法的数学模型和边界条件要尽可能的符合系统的实际情况。

2.原始数据的（系统支撑的刚度系数和阻尼系数）准确度，也是影响计算结果准确度的重要因素。

3.适当的考虑计算速度，随着转子支撑系统的日益复杂，临界转速的计算工作量越来越大，因此选择计算方法的效率也是需要考虑的重要因素。

三、常用的计算方法注：斯托多拉法莫克来斯塔德法传递矩阵法基本原理：传递矩阵法的基本原理是，去不同的转速值，从转子支撑系统的一端开始，循环进行各轴段截面状态参数的逐段推算，直到满足另一端的边界条件。

优点：对于多支撑多元盘的转子系统，通过其特征值问题或通过建立运动微分方程的方法求解系统的临界转速和不平衡响应，矩阵的维数随着系统的自由度的增加而增加，计算量往往较大：采用传递矩阵法的优点是矩阵的维数不随系统的自由度的增加而增大，且各阶临界转速计算方法相同，便于程序实现，所需存储单元少，这就使得传递矩阵法成为解决转子动力学问题的一个快速而有效的方法。

缺点：求解高速大型转子的动力学问题时，有可能出现数值不稳定现象。

今年来提出的Riccati传递矩阵法，保留传递矩阵的所有优点，而且在数值上比较稳定，计算精度高，是一种比较理想的方法，但目前还没有普遍推广。

轴段划分：首先根据支撑系统中刚性支撑（轴承）的个数划分跨度。

在整个轴段内，凡是轴承、集中质量、轮盘、联轴器等所在位置，以及截面尺寸、材料有变化的地方都要划分为轴段截面。

临界转速的计算公司标准化编码 [QQX96QT-XQQB89Q8-NQQJ6Q8-MQM9N]一、临界转速分析的目的临界转速分析的主要目的在于确定转子支撑系统的临界转速，并按照经验或有关的技术规定，将这些临界转速调整，使其适当的远离机械的工作转速，以得到可靠的设计。

例如设计地面旋转机械时，如果工作转速低于其一阶临界转速Nc1，应使N<,如果工作转速高于一阶临界转速，应使<N<+1,而对于航空涡轮发动机，习惯做法是使其最大工作转速偏离转子一阶临界转速的10~20%。

二、选择临界转速计算方法要较为准确的确定出转子支撑系统的临界转速，必须注意以下两点1.所选择的计算方法的数学模型和边界条件要尽可能的符合系统的实际情况。

2.原始数据的（系统支撑的刚度系数和阻尼系数）准确度，也是影响计算结果准确度的重要因素。

3.适当的考虑计算速度，随着转子支撑系统的日益复杂，临界转速的计算工作量越来越大，因此选择计算方法的效率也是需要考虑的重要因素。

莫克来斯塔德法传递矩阵法基本原理：传递矩阵法的基本原理是，去不同的转速值，从转子支撑系统的一端开始，循环进行各轴段截面状态参数的逐段推算，直到满足另一端的边界条件。

优点：对于多支撑多元盘的转子系统，通过其特征值问题或通过建立运动微分方程的方法求解系统的临界转速和不平衡响应，矩阵的维数随着系统的自由度的增加而增加，计算量往往较大：采用传递矩阵法的优点是矩阵的维数不随系统的自由度的增加而增大，且各阶临界转速计算方法相同，便于程序实现，所需存储单元少，这就使得传递矩阵法成为解决转子动力学问题的一个快速而有效的方法。

缺点：求解高速大型转子的动力学问题时，有可能出现数值不稳定现象。

今年来提出的Riccati 传递矩阵法，保留传递矩阵的所有优点，而且在数值上比较稳定，计算精度高，是一种比较理想的方法，但目前还没有普遍推广。

轴段划分：首先根据支撑系统中刚性支撑（轴承）的个数划分跨度。

轴的临界转速计算公式轴的临界转速也称为临界频率，是指转子在转动时出现横向振动的频率，达到一定的转速时会产生严重的振动破坏。

因此，对于设计和选择轴的转速有很重要的意义。

本文将介绍轴的临界转速计算公式，包括理论计算和实际测量方法。

一、理论计算方法轴的临界转速可以用理论计算方法来估算。

这种方法通常基于轴的自然频率和叶轮的惯性力。

我们可以根据叶轮的质量、惯性矩、叶轮与轴的连接方式等参数来计算出叶轮的振动特性，并根据轴的材料属性、截面形状和长度等参数来计算轴的自然频率。

然后，我们可以使用下面的公式来计算轴的临界转速：Ncr = Kcr / （π*D）其中，Ncr为轴的临界转速，单位为rpm；Kcr为轴的临界弯曲刚度，单位为N·m^2；D为轴的直径，单位为m。

这个公式基于轴的弯曲振动模式，假设轴由弹性材料制成且柔度均匀。

因此，由轴截面转换为转子刚度，可以得到下面的数学公式：Kcr = （2*π*fcr）^2 * I / L其中，fcr为轴的临界频率，单位为Hz；I为轴的截面转动惯量，单位为m^4；L为轴的长度，单位为m。

转子的质量和惯性矩均假定为分布均匀，因此I可以计算为轴的截面面积与离心力作用点到轴心的垂直距离之积。

对于均匀截面的圆形轴，其转动惯量计算公式为：I = π*r^4 / 4其中，r为轴半径。

对于矩形截面的轴，其转动惯量可以计算如下：I = bh^3 / 12其中，b为轴的宽度，h为轴的高度。

二、实际测量方法除了理论计算方法外，我们还可以使用实际测量方法来计算轴的临界转速。

这种方法通常涉及使用专用的振动测量仪器来确定轴的振动模式和频率。

在测量之前，我们需要保证轴处于静止状态和固定状态。

然后，我们可以使用如下步骤来进行实际测量：1、使用加速度传感器或振动传感器在轴的相对位置测量振动；2、在轴上施加导轮或质量块用于激起振动，然后记录振动测量结果；3、分析振动数据并确定轴的自然频率和振动模式；4、使用振动模态和自然频率计算轴的临界转速。

电机转速计算公式电机转速计算公式是用来计算电机旋转速度的一个数学公式。

在电机运行过程中，了解电机的转速对于我们正确使用和维护电机都非常重要。

要计算电机转速，我们需要知道几个关键参数：极对数、电机电压和线圈电感。

极对数指的是电机转子上的磁极数。

电机电压是指电机所接收的电压大小，通常以伏特(V)为单位。

线圈电感是指电机线圈在电流变化过程中的抵抗程度，通常以亨利(H)为单位。

通过这些参数，我们可以使用以下的转速计算公式来计算电机的旋转速度：转速（单位：转/分）= （电压× 60）/ （2 ×线圈电感× 极对数）这个公式的核心思想是根据电机电压和线圈电感的变化率来计算电机的转速。

由于电机是通过电压来驱动的，所以电压的变化量与电机转速之间存在着关系。

同时，线圈电感的大小也会对电机转速产生影响。

极对数表示了电机转子上的磁极数，当极对数增加时，电机的转速也会相应增加。

需要注意的是，转速的计算结果以转/分为单位。

这是因为在实际应用中，我们更常用每分钟转数来描述电机的转速。

然而，在使用计算机和数学模型时，我们通常使用转/秒作为单位。

因此，在计算时需要进行单位的转换。

通过转速计算公式，我们可以获得电机的旋转速度。

这对于电机运行监控、调整和控制至关重要。

例如，在工业生产中，电机的转速通常需要保持在一个特定范围内，以确保设备的正常运行。

通过计算电机转速，我们可以及时掌握电机的运行状态，如有需要，及时调整电压或其他参数来达到所需的转速。

此外，电机转速的计算也有助于电机的设计和优化。

通过计算预测电机的转速，我们可以进行理论分析和实验测试，以确定最佳的参数组合和操作条件。

这将有助于提高电机效率、降低能耗和延长电机的使用寿命。

需要注意的是，转速计算公式只是一个理论模型，在实际应用中可能存在误差。

这是由于电机内部结构、外部环境和测量工具的限制等因素所致。

因此，在具体应用中，我们需要根据实际情况进行修正和调整。

临界转速计算公式[宝典]离心机临界转速的计算资讯类型:化工设备加入时间:2006年4月21日17:19l基本公式及计算方法卧式螺旋离心机的轴承属于刚性支承，其简化模型如图3-5所示。

由于卧式螺旋离心机的转鼓和螺旋的刚度比轴大得多，所以可将转鼓和螺旋视为刚体。

又因为转鼓和螺旋的转速不同，所以它们总的回转力矩可按下式近似计算:其临界转速为至今己有多种较为完善的临界转速的计算方法如矩阵迭代法、逐段推算法、能量法等。

但他们难于计算多转子复杂结构的转子系统。

建立在高速计算机基础上的有限元法可以精确计算转子动力学问题，计算过程中数值稳定，但公式推导和编程比较困难，对计算机的内存和机时要求大，不适合通用计算机程序的编制。

传递矩阵法是解决计算转子动力学的又一个有效的方法，它的优点在于传递矩阵的维数不随系统自由度的增加而加大，工程技术人员可以在感兴趣的范围内求得所需要的临界转速和对应的振型;缺点在于计算高阶临界转速、振型和响应时，可能出现数值不稳定的情况。

经典的传递矩阵方法在处理转子的刚性支撑、轴间连接及球形铰链等未知数，建立方程组时，无法克服各种转子复杂多样结构所带来的差异，也就不能顺利编制计算各种转子特性的通用计算程序。

对于复杂转子，它的主要工作是作出临界转速的图谱，以便分析在不同情况下内外转子相互之间激起的临界转速。

为了书写方便引入矩阵了。

上标k表示第k个B矩阵，下标ij表示矩阵B 的第i行第j列元素。

两子系统的两端为自由端，这样边界条件分别为弯矩与剪力等于O，即:上标L表示每一段的左起始截面，上标R表示每一段的右末尾截面，下标L表示螺旋推进器部分，下标Z表示转鼓部分，这样相应的状态矢量的矩阵:式中:K1—第一个支承轴承的弹簧刚度系数。

式中:k2—第二个支承轴承的弹簧刚度系数。

在螺旋推进器部分:在转鼓部分:因此，该方程的系数矩阵的行列式等于0，而该行列式又是ωL和ωz的函数，通过二分法，找出系列给定值ωL时，转鼓激起的ωz1，ωz2，ωz3等临界转速，以及系列给定值妈时，螺旋推进器激起的ωL1，ωL2，ωL3，等临界转速。

电机转速计算公式
电机转速计算公式是指根据电机的基本参数，利用物理定律和开
环计算方法来计算电机转速的公式。

一般来说，电机转速计算公式可以分为三类：
1、根据电动机定子电阻和定子磁密度的关系确定电机的转速：
T=K/2π√(R/LR)
其中 T 为转速，单位为Hz；K为常量，取值在 0.7-3.0 之间；R、LR分别为电机定子电阻和定子磁链接，单位为Ohm。

2、根据电动机启动电流和电机转速关系计算电机转速：
Ts=Ist/Kp
其中，Ts为电机转速，单位为Hz；Ist为电机启动电流，单位为A；Kp为参数，值在0.6~1.6之间。

3、根据电机转子磁密度和电机数字控制器输入电压值确定电机转速：
Vin*n=Bd*α*θ/60
其中，Vin为电机的输入电压值，单位为V；n为电机的极数；Bd
为电机转子磁密度，单位为T；α为线圈电流传递因素，取值在
0.2~0.7之间；θ为转角，单位为°；Ts为转速，单位为Hz。

电机规格与转速计算1. 电机规格简介电机规格是指电机的各项参数和技术指标，它们对于电机的使用和性能具有重要意义。

以下是一些常见的电机规格：- 额定功率：电机的额定输出功率，通常以瓦特（W）为单位。

- 额定电压：电机的额定工作电压，通常以伏特（V）为单位。

- 频率：电机的额定工作频率，通常以赫兹（Hz）为单位。

- 转速：电机的转动速度，通常以转每分钟（rpm）为单位。

2. 转速计算方法2.1. 极对数公式极对数公式是一种常见的计算电机转速的方法，它根据电机的极数和输入电源的频率来计算转速。

公式如下：转速（rpm）= 120 * 频率（Hz） / 极数2.2. 标称速度计算标称速度是指电机在额定电源电压、标准工作条件下的理论转速。

根据电机的额定功率和额定转速，可以使用下述公式计算标称速度：标称速度（rpm）= 60 * 额定功率（W）/ (2π * 额定转速（rpm）)3. 举例说明假设一个电机的极数为4，电源的频率为50Hz。

根据极对数公式可以计算出转速为：转速 = 120 * 50 / 4 = 1500rpm另外，假设一个电机的额定功率为1000W，额定转速为3000rpm。

根据标称速度公式可以计算出标称速度为：标称速度= 60 * 1000 / (2π * 3000) ≈ 31.83rpm注意：以上计算结果仅供参考，实际情况中可能受到电机的设计和应用环境的影响。

4. 总结电机规格和转速计算是电机设计和使用过程中重要的部分。

了解电机的规格参数以及转速计算方法，可以帮助我们选择适合的电机，并合理地使用和维护电机。

以上是对电机规格与转速计算的简要介绍，希望对您有所帮助。

> 注意：以上文字为一般性说明，具体情况还需根据实际需求和专业知识进行考量和计算。