轴临界转速的计算1
- 格式:xls
- 大小:38.00 KB
- 文档页数:1
一、临界转速分析的目的临界转速分析的主要目的在于确定转子支撑系统的临界转速,并按照经验或有关的技术规定,将这些临界转速调整,使其适当的远离机械的工作转速,以得到可靠的设计。
例如设计地面旋转机械时,如果工作转速低于其一阶临界转速Nc1,应使N<0.75Nc1, 如果工作转速高于一阶临界转速,应使 1.4Nck<N<0.7Nck+1,而对于航空涡轮发动机,习惯做法是使其最大工作转速偏离转子一阶临界转速的10~20%。
二、选择临界转速计算方法要较为准确的确定出转子支撑系统的临界转速,必须注意以下两点1.所选择的计算方法的数学模型和边界条件要尽可能的符合系统的实际情况。
2.原始数据的(系统支撑的刚度系数和阻尼系数)准确度,也是影响计算结果准确度的重要因素。
3.适当的考虑计算速度,随着转子支撑系统的日益复杂,临界转速的计算工作量越来越大,因此选择计算方法的效率也是需要考虑的重要因素。
三、常用的计算方法2.Prohl-Myklestad莫克来斯塔德法传递矩阵法基本原理:传递矩阵法的基本原理是,去不同的转速值,从转子支撑系统的一端开始,循环进行各轴段截面状态参数的逐段推算,直到满足另一端的边界条件。
优点:对于多支撑多元盘的转子系统,通过其特征值问题或通过建立运动微分方程的方法求解系统的临界转速和不平衡响应,矩阵的维数随着系统的自由度的增加而增加,计算量往往较大:采用传递矩阵法的优点是矩阵的维数不随系统的自由度的增加而增大,且各阶临界转速计算方法相同,便于程序实现,所需存储单元少,这就使得传递矩阵法成为解决转子动力学问题的一个快速而有效的方法。
缺点:求解高速大型转子的动力学问题时,有可能出现数值不稳定现象。
今年来提出的Riccati 传递矩阵法,保留传递矩阵的所有优点,而且在数值上比较稳定,计算精度高,是一种比较理想的方法,但目前还没有普遍推广。
轴段划分:首先根据支撑系统中刚性支撑(轴承)的个数划分跨度。
一、临界转速分析的目的临界转速分析的主要目的在于确定转子支撑系统的临界转速,并按照经验或有关的技术规定,将这些临界转速调整,使其适当的远离机械的工作转速,以得到可靠的设计。
例如设计地面旋转机械时,如果工作转速低于其一阶临界转速Nc1,应使N<0.75Nc1, 如果工作转速高于一阶临界转速,应使 1.4Nck<N<0.7Nck+1,而对于航空涡轮发动机,习惯做法是使其最大工作转速偏离转子一阶临界转速的10~20%。
二、选择临界转速计算方法要较为准确的确定出转子支撑系统的临界转速,必须注意以下两点1.所选择的计算方法的数学模型和边界条件要尽可能的符合系统的实际情况。
2.原始数据的(系统支撑的刚度系数和阻尼系数)准确度,也是影响计算结果准确度的重要因素。
3.适当的考虑计算速度,随着转子支撑系统的日益复杂,临界转速的计算工作量越来越大,因此选择计算方法的效率也是需要考虑的重要因素。
三、常用的计算方法2.Prohl-Myklestad莫克来斯塔德法传递矩阵法基本原理:传递矩阵法的基本原理是,去不同的转速值,从转子支撑系统的一端开始,循环进行各轴段截面状态参数的逐段推算,直到满足另一端的边界条件。
优点:对于多支撑多元盘的转子系统,通过其特征值问题或通过建立运动微分方程的方法求解系统的临界转速和不平衡响应,矩阵的维数随着系统的自由度的增加而增加,计算量往往较大:采用传递矩阵法的优点是矩阵的维数不随系统的自由度的增加而增大,且各阶临界转速计算方法相同,便于程序实现,所需存储单元少,这就使得传递矩阵法成为解决转子动力学问题的一个快速而有效的方法。
缺点:求解高速大型转子的动力学问题时,有可能出现数值不稳定现象。
今年来提出的Riccati 传递矩阵法,保留传递矩阵的所有优点,而且在数值上比较稳定,计算精度高,是一种比较理想的方法,但目前还没有普遍推广。
轴段划分:首先根据支撑系统中刚性支撑(轴承)的个数划分跨度。

轴的临界转速计算公式轴的临界转速是指当轴在旋转时,其转速达到一定数值时会发生共振或失稳现象。
这一现象对于机械系统的设计和运行都具有重要的意义,因为超过临界转速会导致机械系统的破坏和故障。
因此,准确计算轴的临界转速非常重要。
轴的临界转速计算公式是通过考虑轴的材料、几何形状、边界条件等参数来推导得出的。
在推导公式之前,我们需要了解一些与轴有关的基本概念和理论。
首先,轴的弯曲振动是指轴在受到外力作用下发生的弯曲变形。
这种变形会导致轴产生弯曲应变和应力,当外力作用足够大时,轴的弯曲振动会导致共振或失稳现象的发生。
其次,轴的临界转速与其的自然频率有关。
自然频率是指轴在没有外力作用下,自由振动的频率。
当轴的转速接近或等于自然频率时,共振现象就会发生。
根据振动理论,轴的自然频率可以通过以下公式计算:f = (1/2π) * √(k/m)其中,f为自然频率,k为轴的弯曲刚度,m为轴的质量。
在轴的自然频率计算中,我们需要考虑轴的几何形状和材料参数。
轴的几何形状包括直径、长度和截面形状等。
轴的材料参数包括弹性模量和密度等。
这些参数可以通过实验测量或材料手册查找获得。
当我们计算出轴的自然频率后,就可以通过以下公式计算轴的临界转速:Nc = (f * 60) / p其中,Nc为轴的临界转速,f为自然频率,p为轴的极角。
值得注意的是,以上公式仅适用于简单的轴系统,对于复杂的轴系统,如多段轴或弯曲-扭转耦合系统,需要考虑更多的参数和复杂的计算方法。
最后,为了确保轴的安全运行,我们需要将计算得到的临界转速与实际运行转速进行比较。
如果实际运行转速接近或超过临界转速,就需要采取相应的措施,如增加轴的刚度、改变轴的几何形状或调整轴的支撑方式等,以降低轴的振动和共振风险。
总结起来,轴的临界转速计算公式是根据轴的自然频率和极角等参数推导得出的。
这一公式能够帮助我们了解和预测轴的振动和共振现象,从而采取相应的措施确保轴的安全运行。
然而,需要注意的是,公式适用于简单的轴系统,对于复杂的轴系统需要采用更加细致和复杂的计算方法。

转轴的挠度及临界转速计算程序(一具有集中载荷的两支点轴承的计算(如图2-118转轴重量: Q=285(kg L1=49转子重量: G1=365(kg L2=52.1铁心有效长度:L fe=46(cm L=126转子外径: D1=37.2(cm La=36单边气隙: δ=0.4(cm G2=20弹性模量: E= 2.06E+06(MPay=0.388888889气隙磁密: Bδ=5781GS z=0.285714286同步转速: n=5000r/min根据y、z值查图2-119功率: P=300kWθ=0.5过载系数: K= 2.25b处轴径212、挠度系数计算:单位:cm cm4cm cm3cm3轴a~b段d i J i X i Xi 3Xi3-X(i-1319321.89906251533753375 210490.62522.511390.638015.625 311718.324062526.518609.637219 4121017.3633.537595.3818985.75 5131401.27406342.576765.6339170.25 6141884.78547.5107171.930406.25 7000008000009000001000000∑ K ab=轴c~b段d i J i X i Xi 3Xi3-X(i-1318200.96 4.591.12591.125 29321.89906259.5857.375766.25311718.324062518.56331.6255474.25 4131401.27406327.520796.8814465.25 5141884.78532.534328.1313531.25 600000 700000 800000 900000 1000000∑ K cb=3、轴在b点的柔度:αbb= 3.44022E-06cm/kg一、绕度及临界转速计算4、磁拉力刚度:K0=8753.301622kg/cm5、初始单边磁拉力:P0=350.1320649kg6、由G1重量引起的b点绕度:f1=0.001875367cm7、滑环重量G2引起的b点绕度:f2=7.67363E-05cm8、单边磁拉力引起的b点绕度:fδ=0.001883694cm9、轴在b点的总绕度:f=0.003835798cm应小于异步电机同步电机10、转轴临界转速:n kp=6635.556016rpm二、轴的强度计算:1、最大转矩:Mmax=1289.25N.m2、bb点处的弯矩:Mbb=1419.958282N.m3、bb处的交变弯矩应力:ζbb=1533266.691N/m24、bb处的剪切应力:ηbb=696064.1399N/m2ηn=348032.07N/m2脉动循环下的剪切应力:η∞=870080.1749N/m25、轴在bb处受到的总负荷应力:ζ= 2.319281093N/mm2应该小于材料许用[ζ]=三、轴承计算:1、转子所受最大径向力:W=715.1320649kg2、a处轴承支承力:Pa=295.7014332kg3、c处轴承支承力:Pc=278.1069141kg4、轴承寿命:Lh=35986600.69小时应大于10^5式中:ε=3.33f t=1载荷系数F f=1.1温度系数c=39600轴承额定动负荷P i=278.11当量动负荷(二带外伸端的两支点轴承的计算(如图2-120一、基本参数:电枢重量(G1包括转轴中部重量的2/3和滑环的重量在内一、绕度及临界转速计算2、柔度系数计算:3、轴的柔度:α11=7.56093E-07cm/kgα22= 2.42497E-06cm/kgα12=-8.91046E-07cm/kgα21=-8.91046E-07cm/kg4、转子重量所引起的挠度:b处:f1'=0.006714438cmd处:f2'=-0.006606742cm5、磁拉力刚度:转子一:K1=136812.9233kg/cm转子二:K2=0kg/cm6、初始磁拉力:P1=1368.129233kgP2=0kg7、由磁拉力引起的挠度:F0= 1.03954E-12E0=0.896556679b处:f1"=0.001153785cmd处:f2"=-0.001359721cm8、总挠度:同步机b处:f1=0.007868222cm应该<0.008d处:f2=-0.007966462cm应该<0 9、临界转速:一次:n k=3506.387398rpm应该>975 速计算程序(如图2-118(cm(cm(cm(cm(kg曲线cmcm-1[X i3-X(i-13]/J i10.4846530916.3375796210.0497816718.6617814727.9533112416.1324766599.61958374[X i3-X(i-13]/J i0.4534484472.3804045727.62086401610.32292717.17920081127.956844950.04cm0.032cm55N/mm2小时图2-120(cm(cm(cm(cmMpa[X i3-X(i-13]/J i X i2X i2-X(i-12[X i2-X(i-12]/J i X i-X i-1(X i-X i-1/J i0.918664587-0.3518347250.3368560430.903685905[X i3-X(i-13]/J i X i2X i2-X(i-12[X i2-X(i-12]/J i X i-X i-1(X i-X i-1/J i 0.056840583204204.490.00397486614.30.00027796311.2813244395459340.80.1133507583.40.00101206-0.5198816461089-8456.29-0.004903061-64.7-3.75139E-0500-10890-330000000000000000000000000异步机cm应该<0.01cm cm应该<0cm rpm满足要求。
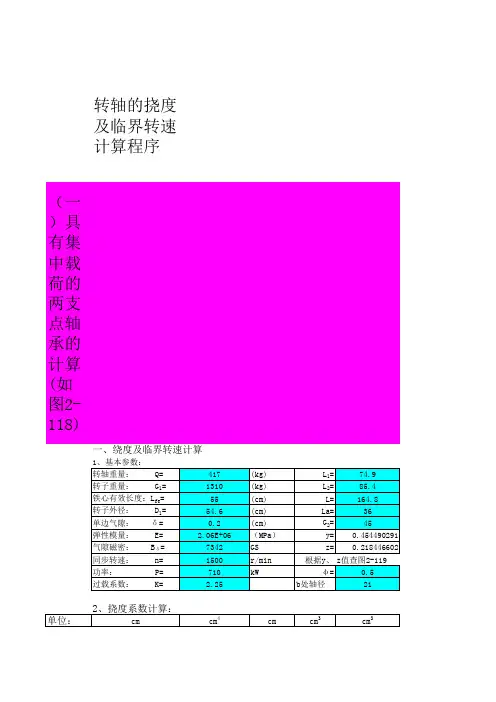
转轴的挠度及临界转速计算程序(一)具有集中载荷的两支点轴承的计算(如图2-118)一、绕度及临界转速计算3、轴在b点的柔度:αbb= 4.99225E-06cm/kg4、磁拉力刚度:K0=49554.06333kg/cm5、初始单边磁拉力:P0=991.0812667kg6、由G1重量引起的b点绕度:f1=0.007881595cm7、滑环重量G2引起的b点绕度:f2=0.000163144cm8、单边磁拉力引起的b点绕度:fδ=0.008495762cm9、轴在b点的总绕度:f=0.016540502cm应小于异步电机同步电机10、转轴临界转速:n kp=2802.141933rpm二、轴的强度计算:1、最大转矩:Mmax=10170.75N.m2、bb点处的弯矩:Mbb=8752.669171N.m3、bb处的交变弯矩应力:σbb=9451105.897N/m24、bb处的剪切应力:τbb=5491172.66N/m2τn=2745586.33N/m2脉动循环下的剪切应力:τ∞=6863965.824N/m25、轴在bb处受到的总负荷应力:σ=16.66671863N/mm2应该小于材料许用[σ]=三、轴承计算:1、转子所受最大径向力:W=2301.081267kg2、a处轴承支承力:Pa=1192.429249kg3、c处轴承支承力:Pc=1045.819095kgLh=1456982.883小时 应大于10^5式中:ε=3.33f t=1载荷系数F f=1.1温度系数c=39600轴承额定动负荷P i=1045.82当量动负荷4、轴承寿命:(二)带外伸端的两支点轴承的计算(如图2-120)一、基本参数:电枢重量(G1包括转轴中部重量的2/3和滑环的重量在内)一、绕度及临界转速计算2、柔度系数计算:3、轴的柔度:α11=7.56093E-07cm/kgα22= 2.42497E-06cm/kgα12=-8.91046E-07cm/kgα21=-8.91046E-07cm/kg4、转子重量所引起的挠度:b处:f1'=0.006714438cmd处:f2'=-0.006606742cm5、磁拉力刚度:转子一:K1=136812.9233kg/cm转子二:K2=0kg/cm6、初始磁拉力:P1=1368.129233kgP2=0kg7、由磁拉力引起的挠度:F0= 1.03954E-12E0=0.896556679b处:f1"=0.001153785cmd处:f2"=-0.001359721cm8、总挠度:同步机b处:f1=0.007868222cm应该<0.008d处:f2=-0.007966462cm应该<09、临界转速:一次:n k=3506.387398rpm应该>975(cm)(cm)(cm)(cm)(kg)曲线cmcm-1[X i3-X(i-1)3]/J i0.0158060470.6150555471.00413328510.3702657246.3391216458.34438224[X i3-X(i-1)3]/J i0.0158060474.2301062568.2384035378.674287214.41912717947.9333411973.511071410.02cm0.016cm55N/mm 2小时(cm)(cm)(cm)(cm)Mpa异步机cm应该<0.01cm cm应该<0cmrpm满足要求。

轴用弹性挡圈临界转速计算分析轴用弹性挡圈临界转速计算分析轴用弹性挡圈是一种常见的轴向定位和传动装置,常常应用于各种机械设备和工业生产中。
在这种装置中,弹性挡圈作为轴的固定件,起到定位轴的作用,同时可以承受一定的载荷。
当轴旋转速度达到一定值时,弹性挡圈会因受到过大的离心力而发生变形或断裂,造成设备故障和安全事故。
因此,准确计算轴用弹性挡圈的临界转速具有重要意义,可以保障设备的正常运行和安全性。
弹性挡圈的变形与断裂与其材料、几何形状、工作方式、载荷等因素有关。
一般来说,弹性挡圈的工作方式可分为三种:扭转型、弯曲型和波纹管型。
其中,扭转型弹性挡圈的临界转速最高,波纹管型最低。
弹性挡圈的材料主要有金属、橡胶、塑料等,金属材料的强度高、刚度大,耐久性好,但容易疲劳变形;橡胶材料具有良好的弹性,但耐久性差;塑料材料轻便且易于制造,但强度和刚度较低。
因此,选取适宜的弹性挡圈材料和工作方式对于临界转速的计算具有重要影响。
在计算临界转速时,需先确定弹性挡圈的固有频率和临界转速系数。
固有频率是指弹性挡圈在其自然状态下的振动频率,通常以赫兹(Hz)为单位。
临界转速系数是指弹性挡圈在其允许转速范围内,允许的最高转速与典型工作转速的比值。
一般来说,临界转速系数应在0.9-1.2之间,若超过此范围,弹性挡圈将过早地产生变形或失效。
在实际计算中,还需考虑弹性挡圈的载荷、几何形状等因素。
若弹性挡圈的轴向载荷过大,会导致挠曲或疲劳失效;若几何形状设计不当,会使其在高速旋转时受到过大的离心力而断裂或变形。
因此,在设计弹性挡圈时应严格遵循相关标准和经验公式,并对其合理性进行验证和测试,以确保其安全可靠性。
综上所述,轴用弹性挡圈的临界转速是一个非常重要的技术问题,涉及的因素很多、非常复杂。
在实际生产中,需采用科学的方法进行计算、分析和验证,以确保其在工作过程中能够满足设计要求,并保证设备的安全可靠性。
轴用弹性挡圈的临界转速计算中需要考虑的相关数据包括弹性挡圈的材料、几何形状、工作方式、载荷等因素,以及弹性挡圈的固有频率和临界转速系数。

YE6254转子动力学教学实验系统资料一:转子轴系临界转速计算1.转子轴系参数:转轴:Φ10×320 mm,3根,Φ10×500 mm,1根(油膜振荡用),材料为40C;r 转盘:Φ76×25mm,质量800g;Φ76×19mm,质量600g,材料为40Cr;跨度:Φ10×320 mm转轴为250mm;Φ10×500 mm转轴为430mm;连接方式:柔性和刚性两种连轴方式,且按照不同的组合;材料参数:弹性模量为210GPa,密度为7800kg/m3;给定参数:柔性连接刚度取100N/ m2 ,刚性连接则认为轴是连接在一起的。
2.计算方法:对转子轴系临界转速的理论计算采用Riccati传递矩阵法,传递矩阵法的详细介绍见资料二。
3.计算结果:按照所选取的转子轴系参数,采用Riccati传递矩阵法,计算了36种转子轴系组合情形的临界转速,结果见下表。
表中给出的是转盘在转轴特定位置的临界转速,即对单轴单盘,转盘在转轴跨长的中间位置;对单轴双盘,两转盘分别在转轴跨长的1/3位置。
转盘可安装在转轴的任意位置,其他位置的定性结论是:对单轴单盘,若转盘不在跨长的中间位置,临界转速会提高;对单轴双盘,对称位置是两转盘在跨长的1/3处,若两转盘均向支承点方向做小幅度移动,则一阶临界转速会提高,二阶临界转速会降低,若两转盘均向转轴中间方向做小幅度移动,则一阶临界转速会降低,二阶临界转速会提高;柔性连接的各阶临界转速均低于刚性连接,且一阶临界转速变化比较明显。
3.1 单轴单盘:表1:3.2 单轴双盘:表2:表3:3.3 双轴双盘:表4:表6:表7:3.4 三轴三盘:表8:3.5双轴三盘:表10:表11:附:转子轴系临界转速计算图形2单轴单盘:盘居中,320mm轴,800g盘,临界转速约为5728rmp4单轴单盘:盘居中,500mm轴,800g盘,临界转速约为2472rmp5单轴单盘:盘位于1/3处,500mm轴,800g盘,临界转速约为2814rmp6单轴双盘:两盘位于1/3处,320mm轴,600g盘两个,临界转速一阶约为5436rmp,二阶约为21307rmp一阶约为5062rmp,二阶约为20039rmp8单轴双盘:两盘位于1/3处,320mm轴,800g盘两个,临界转速一阶约为4762rmp,二阶约为18613rmp盘各一个,临界转速10单轴双盘:两盘位于1/5处,320mm轴,600g、800g6858rmp ,二阶约为17024rmp0.51 1.52x 104-1-0.50.51x 101112 单轴双盘:两盘位于1/3处,500mm 轴,600g 盘两个,临界转速一阶约为2345rmp ,二阶约为9343rmp13单轴双盘:两盘位于1/3处,500mm轴,600g、800g盘各一个,临界转速一阶约为2192rmp,二阶约为8786rmp14单轴双盘:两盘位于1/3处,500mm轴,800g盘两个,临界转速一阶约为2067rmp,二阶约为8181rmp15单轴双盘:两盘距两侧支承点各1/4轴跨度长,500mm轴,800g盘两个,临界转速一阶约为2491rmp,二阶约为7232rmp16单轴双盘:两盘距两侧支承点各2/5轴跨度长,500mm轴,800g盘两个,临界转速一阶约为1894rmp,二阶约为11874rmp临界转速一阶约为6741rmp,二阶约为9095rmp18双轴双盘:轴间柔性连接,盘位于各轴中间,320mm轴两根,600g、800g 盘各一个,临界转速一阶约为6551rmp,二阶约为8208rmp临界转速一阶约为5925rmp ,二阶约为7976rmp20 双轴双盘:轴间柔性连接,盘位于各轴中间,500mm 轴和320mm 轴各一根, 0200040006000800010000-1-0.50.51x 1011600g 、800g 盘各一个,临界转速一阶约为3821rmp ,二阶约为6252rmp0200040006000800010000-1-0.50.51x 101122 双轴双盘:轴间柔性连接,盘位于各轴中间,500mm 轴和320mm 轴各一个,800g 盘两个,临界转速一阶约为3388rmp ,二阶约为6228rmp24双轴双盘:轴间刚性连接,盘位于各轴中间,320mm轴两根,600g、800g临界转速一阶约为7410rmp ,二阶约为8105rmp26 双轴双盘:轴间刚性连接,盘位于各轴中间,500mm 轴和320mm 轴各一个, 0200040006000800010000-1-0.50.51x 1011320mm轴各一个,28双轴双盘:轴间刚性连接,盘位于各轴中间,500mm轴和临界转速一阶约为6771rmp,二阶约为8338rmp,三阶约为10008rmp30三轴三盘:轴间柔性连接,盘位于各轴中间,320mm轴三根,800g盘三个,临界转速一阶约为5951rmp,二阶约为7315rmp,三阶约为8773 rmp临界转速一阶约为8706rmp ,二阶约为8847rmp ,三阶约为11151 rmp020004000600080001000012000-1-0.50.51x 101132 三轴三盘:轴间刚性连接,盘位于各轴中间,320mm 轴三根,800g 盘三个,临界转速一阶约为7640rmp ,二阶约为7761rmp ,三阶约为9772 rmp转盘,分位于1/3处,320mm轴置1转盘,位于轴中间,600g盘三个,临界转速一阶约为3277rmp,二阶约为7035rmp,三阶约为10600 rmp34双轴三盘:轴间柔性连接,500mm轴和320mm轴各一个,500mm轴置2转盘,分位于1/3处,320mm轴置1转盘,位于轴中间,800g盘三个,临9282 rmp界转速一阶约为2887rmp,二阶约为6177rmp,三阶约为转盘,分位于1/3处,320mm轴置1转盘,位于轴中间,600g盘三个,临界转速一阶约为3365rmp,二阶约为8815rmp,三阶约为10600 rmp转盘,分位于1/3处,320mm轴置1转盘,位于轴中间,800g盘三个,临界转速一阶约为2964rmp,二阶约为7730rmp,三阶约为9282 rmp。

汽车传动轴临界转速的有限元法计算季 钢摘要 用有限元方法分析和计算汽车传动轴的临界转速,给出了相应的计算模型,并将计算的结果与实验结果相比较,为传动轴的设计与其临界转速的测定和计算提供了一种新的方法。
关键词:汽车传动轴 临界转速 有限元汽车传动轴的临界转速直接关系到汽车的高速性与平稳性。
传动轴系统在常用转速区出现共振,会使轴系和传动齿轮承受极大的交变冲击力,发生较强的机械振动与噪声,严重时还会导致断轴或断齿,造成事故。
目前国内较注重传动轴的动平衡,但对传动轴的共振频率的分布却研究甚少。
而事实上在大多数情况下,共振问题的产生往往是由于传动系统自振频率布置不当造成的,为了避免发生共振,通常可以修正系统的动力学参数(例如转动惯量和轴段与部件的刚度等),调整自振频率。
这些工作若能在汽车动力传动轴系的设计阶段加以解决,则最为经济和方便。
计算传动轴的临界转速相当于计算它的固有频率,计算轴系的固有频率有很多方法,本文介绍有限元方法进行分析和计算。
一、有限元法动力分析有限元法是最近三四十年发展起来的一门数值分析技术,是借助高速电子计算机解场问题的近似计算方法。
它运用离散的概念,使整个问题由整体连续到分段连续,由整体解析转化为分段解析,从而使数值法与解析法互相结合,互相渗透,形成一种新的数值计算方法。
首先把连续体离散化,把连续体假想分割成数目有限的小块单元,而单元之间只在数目有限的指定点处相互连结。
其次,选择一个较简单的函数来近似地表示其位移的分布规律,并用物理学中的基本方程建立起单元上节点力与位移的关系。
最后,借助于矩阵方法集合起来,利用各种方法求解方程组,得到所要求的结果。
动力学分析是有限元法的一个重要应用范围,结构的动力方程可由节点平衡条件来导出。
节点上的作用力可分为两类,作用于节点上的外载荷与相关单元对该节点的作用力。
汇集所有的节点方程,便得到结构的动力平衡方程,用矩阵符号可表示为: [M][ ]+[C][ ]+[K][ ]=[R](1)!!!其中[ ],[],[ ]分别是结构的节点位移、节点速度、节点加速度向量;[R]是结构的整体载荷向量,是t的函数;[K]是结构的整体刚度矩阵,由各个单元刚度矩阵集合而成;[C]是结构的整体阻尼矩阵,由各个单元阻尼矩阵集合而成;[M]是结构的整体质量矩阵,由各个单元质量矩阵集合而成;式(1)是用有限元法求解结构动力问题的基本方程,它是一个大型的二阶常微分方程组,简称为动力方程。

轴的第一临界转速作为机械制造行业中的一个重要部件,轴经常会出现各种的问题。
在制造和使用过程中,一些常见的轴问题包括轴断裂、轴弯曲以及轴磨损等等。
而在轴的设计和制造中,临界转速是一个非常重要的因素,需要特别注意。
本文将重点介绍轴的第一临界转速。
一、什么是轴的临界转速?临界转速是指轴转速的某一值,当轴转速达到这个值时,轴身的弯曲振动会变得非常严重,也就是说,轴的波形将表现出明显的波动形状,从而影响了轴的正常工作。
在工程学中,临界转速通常用来描述某个系统的安全运行边界。
二、轴的临界转速的计算方法在设计和制造一个轴时,需要首先计算出轴的临界转速。
一般情况下,轴的临界转速可以按照下面的公式计算得到:Nc=K×√(EI/(ρA))式中,Nc是轴的临界转速,K是一个系数,通常取值为1.2到2.5之间,EI是轴的弯曲刚度,ρ是轴材料的密度,A是轴的截面积。
三、轴的第一临界转速的意义轴的第一临界转速是指轴在没有扭矩作用下的临界转速。
当轴的转速超过第一临界转速时,轴身会出现弯曲振动,这会导致轴的疲劳寿命缩短,从而直接影响轴的可靠性和使用寿命。
因此,在实际制造中,需要尽可能保证轴的第一临界转速低于工作转速。
四、如何提高轴的临界转速为了提高轴的临界转速,可以从以下三个方面进行优化:1、材料的选择。
使用高强度材料可以提高轴的临界转速,例如使用合金钢,可使轴的强度提高20%~30%。
2、减小轴的尺寸。
轴的强度和刚度与其截面积和惯性矩有关,可以通过减小轴的最小截面尺寸来提高轴的临界转速。
3、改变轴的结构。
可以采用镟削、淬火等制造技术来调整轴的结构,提高其临界转速。
总之,轴的第一临界转速是轴制造中非常重要的一个参数。
合理计算和设计各项参数,可以有效提高轴的强度和使用寿命,从而保证轴在工作中的稳定性和可靠性。
临界转速分析的主要目的在于确定转子支撑系统的临界转速,并按照经验或有关的技术规定,将这些临界转速调整,使其适当的远离机械的工作转速,以得到可靠的设计。
例如设计地面旋转机械时,如果工作转速低于其一阶临界转速Nc1,应使N<,如果工作转速高于一阶临界转速,应使<N<+1,而对于航空涡轮发动机,习惯做法是使其最大工作转速偏离转子一阶临界转速的10~20%。
一、选择临界转速计算方法要较为准确的确定出转子支撑系统的临界转速,必须注意以下两点1.所选择的计算方法的数学模型和边界条件要尽可能的符合系统的实际情况。
2.原始数据的(系统支撑的刚度系数和阻尼系数)准确度,也是影响计算结果准确度的重要因素。
3.适当的考虑计算速度,随着转子支撑系统的日益复杂,临界转速的计算工作量越来越大,因此选择计算方法的效率也是需要考虑的重要因素。
二、常用的计算方法注:斯托多拉法莫克来斯塔德法传递矩阵法基本原理:传递矩阵法的基本原理是,去不同的转速值,从转子支撑系统的一端开始,循环进行各轴段截面状态参数的逐段推算,直到满足另一端的边界条件。
优点:对于多支撑多元盘的转子系统,通过其特征值问题或通过建立运动微分方程的方法求解系统的临界转速和不平衡响应,矩阵的维数随着系统的自由度的增加而增加,计算量往往较大:采用传递矩阵法的优点是矩阵的维数不随系统的自由度的增加而增大,且各阶临界转速计算方法相同,便于程序实现,所需存储单元少,这就使得传递矩阵法成为解决转子动力学问题的一个快速而有效的方法。
缺点:求解高速大型转子的动力学问题时,有可能出现数值不稳定现象。
今年来提出的Riccati 传递矩阵法,保留传递矩阵的所有优点,而且在数值上比较稳定,计算精度高,是一种比较理想的方法,但目前还没有普遍推广。
轴段划分:首先根据支撑系统中刚性支撑(轴承)的个数划分跨度。
在整个轴段内,凡是轴承、集中质量、轮盘、联轴器等所在位置,以及截面尺寸、材料有变化的地方都要划分为轴段截面。
临界转速的计算————————————————————————————————作者:————————————————————————————————日期:一、临界转速分析的目的临界转速分析的主要目的在于确定转子支撑系统的临界转速,并按照经验或有关的技术规定,将这些临界转速调整,使其适当的远离机械的工作转速,以得到可靠的设计。
例如设计地面旋转机械时,如果工作转速低于其一阶临界转速Nc1,应使N<0.75N c1,如果工作转速高于一阶临界转速,应使1.4Nck<N<0.7Nck+1,而对于航空涡轮发动机,习惯做法是使其最大工作转速偏离转子一阶临界转速的10~20%。
二、选择临界转速计算方法要较为准确的确定出转子支撑系统的临界转速,必须注意以下两点1.所选择的计算方法的数学模型和边界条件要尽可能的符合系统的实际情况。
2.原始数据的(系统支撑的刚度系数和阻尼系数)准确度,也是影响计算结果准确度的重要因素。
3.适当的考虑计算速度,随着转子支撑系统的日益复杂,临界转速的计算工作量越来越大,因此选择计算方法的效率也是需要考虑的重要因素。
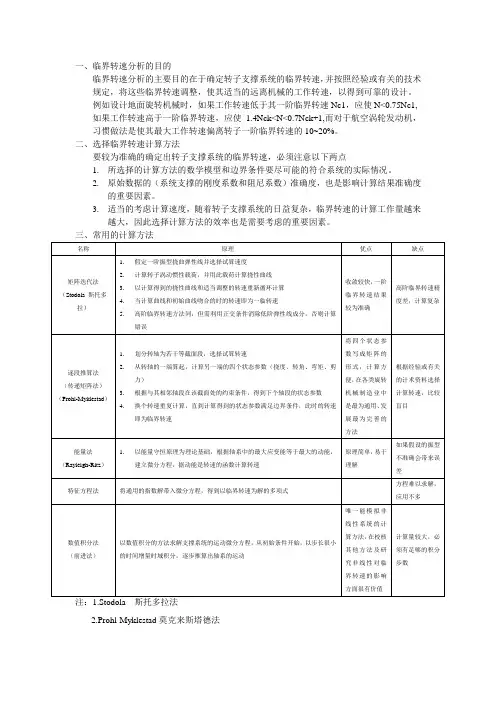
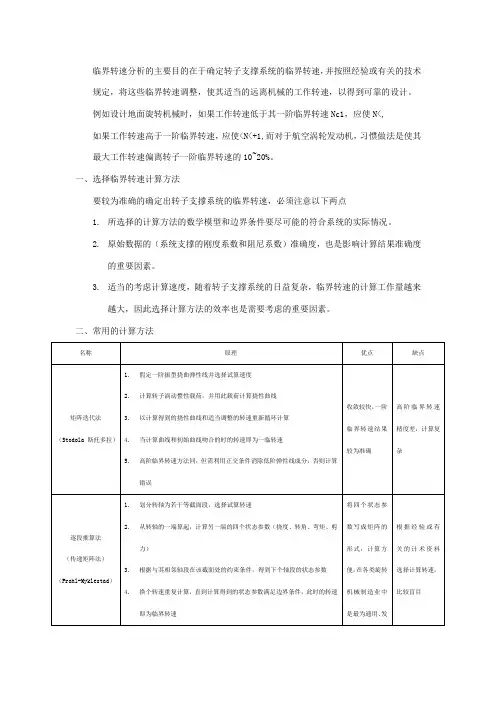
三、常用的计算方法名称原理优点缺点矩阵迭代法(Stodola 斯托多拉)1.假定一阶振型挠曲弹性线并选择试算速度2.计算转子涡动惯性载荷,并用此载荷计算挠性曲线3.以计算得到的挠性曲线和适当调整的转速重新循环计算4.当计算曲线和初始曲线吻合的时的转速即为一临转速5.高阶临界转速方法同,但需利用正交条件消除低阶弹性线成分,否则计算错误收敛较快,一阶临界转速结果较为准确高阶临界转速精度差,计算复杂逐段推算法(传递矩阵法)(Prohl-Myklestad) 1.划分转轴为若干等截面段,选择试算转速2.从转轴的一端算起,计算另一端的四个状态参数(挠度、转角、弯矩、剪力)3.根据与其相邻轴段在该截面处的约束条件,得到下个轴段的状态参数4.换个转速重复计算,直到计算得到的状态参数满足边界条件,此时的转速即为临界转速将四个状态参数写成矩阵的形式,计算方便,在各类旋转机械制造业中是最为通用、发展最为完善的方法根据经验或有关的计术资料选择计算转速,比较盲目能量法(Rayleigh -Ritz)1.以能量守恒原理为理论基础,根据轴系中的最大应变能等于最大的动能,建立微分方程,据动能是转速的函数计算转速原理简单,易于理解如果假设的振型不准确会带来误差特征方程法将通用的指数解带入微分方程,得到以临界转速为解的多项式方程难以求解,应用不多数值积分法(前进法) 以数值积分的方法求解支撑系统的运动微分方程,从初始条件开始,以步长很小的时间增量时域积分,逐步推算出轴系的运动唯一能模拟非线性系统的计算方法,在校核其他方法及研究非线性对临界转速的影响方面很有价值计算量较大,必须有足够的积分步数注:1.Stodola 斯托多拉法2.Prohl-Myklestad莫克来斯塔德法传递矩阵法基本原理:传递矩阵法的基本原理是,去不同的转速值,从转子支撑系统的一端开始,循环进行各轴段截面状态参数的逐段推算,直到满足另一端的边界条件。
转轴的挠度及临界转速计算程序(一)具有集中载荷的两支点轴承的计算(如图2-118)转轴重量: Q=285(kg) L1=49转子重量: G1=365(kg) L2=52.1铁心有效长度:L fe=46(cm) L=126转子外径: D1=37.2(cm) La=36单边气隙: δ=0.4(cm) G2=20弹性模量: E= 2.06E+06(MPa)y=0.388888889气隙磁密: Bδ=5781GS z=0.285714286同步转速: n=5000r/min根据y、z值查图2-119功率: P=300kWθ=0.5过载系数: K= 2.25b处轴径212、挠度系数计算:单位:cm cm4cm cm3cm3轴a~b段d i J i X i Xi 3Xi3-X(i-1)319321.89906251533753375210490.62522.511390.638015.625311718.324062526.518609.6372194121017.3633.537595.3818985.755131401.27406342.576765.6339170.256141884.78547.5107171.930406.257000008000009000001000000∑ K ab=轴c~b段d i J i X i Xi 3Xi3-X(i-1)318200.96 4.591.12591.125 29321.89906259.5857.375766.25 311718.324062518.56331.6255474.25 4131401.27406327.520796.8814465.25 5141884.78532.534328.1313531.25 600000 700000 800000 900000 1000000∑ K cb=3、轴在b点的柔度:αbb= 3.44022E-06cm/kg一、绕度及临界转速计算4、磁拉力刚度:K0=8753.301622kg/cm5、初始单边磁拉力:P0=350.1320649kg6、由G1重量引起的b点绕度:f1=0.001875367cm7、滑环重量G2引起的b点绕度:f2=7.67363E-05cm8、单边磁拉力引起的b点绕度:fδ=0.001883694cm9、轴在b点的总绕度:f=0.003835798cm应小于异步电机同步电机10、转轴临界转速:n kp=6635.556016rpm二、轴的强度计算:1、最大转矩:Mmax=1289.25N.m2、bb点处的弯矩:Mbb=1419.958282N.m3、bb处的交变弯矩应力:ζbb=1533266.691N/m24、bb处的剪切应力:ηbb=696064.1399N/m2ηn=348032.07N/m2脉动循环下的剪切应力:η∞=870080.1749N/m25、轴在bb处受到的总负荷应力:ζ= 2.319281093N/mm2应该小于材料许用[ζ]=三、轴承计算:1、转子所受最大径向力:W=715.1320649kg2、a处轴承支承力:Pa=295.7014332kg3、c处轴承支承力:Pc=278.1069141kg4、轴承寿命:Lh=35986600.69小时 应大于10^5式中:ε=3.33f t=1载荷系数F f=1.1温度系数c=39600轴承额定动负荷P i=278.11当量动负荷(二)带外伸端的两支点轴承的计算(如图2-120)一、基本参数:电枢重量(G1包括转轴中部重量的2/3和滑环的重量在内)一、绕度及临界转速计算2、柔度系数计算:3、轴的柔度:α11=7.56093E-07cm/kgα22= 2.42497E-06cm/kgα12=-8.91046E-07cm/kgα21=-8.91046E-07cm/kg4、转子重量所引起的挠度:b处:f1'=0.006714438cmd处:f2'=-0.006606742cm5、磁拉力刚度:转子一:K1=136812.9233kg/cm转子二:K2=0kg/cm6、初始磁拉力:P1=1368.129233kgP2=0kg7、由磁拉力引起的挠度:F0= 1.03954E-12E0=0.896556679b处:f1"=0.001153785cmd处:f2"=-0.001359721cm8、总挠度:同步机b处:f1=0.007868222cm应该<0.008d处:f2=-0.007966462cm应该<09、临界转速:一次:n k=3506.387398rpm应该>975速计算程序(如图2-118)(cm)(cm)(cm)(cm)(kg)曲线cmcm-1[X i3-X(i-1)3]/J i10.4846530916.3375796210.0497816718.6617814727.9533112416.1324766599.61958374[X i3-X(i-1)3]/J i0.4534484472.3804045727.62086401610.32292717.17920081127.956844950.04cm0.032cm55N/mm2小时图2-120)(cm)(cm)(cm)(cm)Mpa[X i3-X(i-1)3]/J i X i2X i2-X(i-1)2[X i2-X(i-1)2]/J i X i-X i-1(X i-X i-1)/J i0.918664587-0.3518347250.3368560430.903685905[X i3-X(i-1)3]/J i X i2X i2-X(i-1)2[X i2-X(i-1)2]/J i X i-X i-1(X i-X i-1)/J i0.056840583204204.490.00397486614.30.00027796311.2813244395459340.80.1133507583.40.00101206-0.5198816461089-8456.29-0.004903061-64.7-3.75139E-0500-10890-330000000000000000000000000异步机cm应该<0.01cm cm应该<0cmrpm满足要求。
一.轴的挠度及临界转速、强度、刚度计算书(一)、轴的挠度及临界转速计算1.转子重量:G=38000Kg2.有效铁心长度:L=109cm3.转子外径:D=288.6cm4.转轴的简化图形如图1所示图1 转轴简化图形5.单边平均气隙:δ=0.22cm6.轴在b点的挠度系数:αbb =62622221221017.11.43110238.241.1791.82523-⨯=⨯⨯⨯⨯+⨯=⨯+⨯EL K L K L cb ab 7. 磁拉力刚度 k 0=cm Kg B DLs /73257)70005160(7.01096.2883)7000(322=⨯⨯⨯=δ8. 初始单边磁拉力P 0=k 0.e 0=73257×0.1×0.7=5153Kg 9. 由重量G 引起在b 点的挠度: f 1=G αbb =2200×16.8×10-6=0.03696cm 10. 单边磁拉力引起轴在b 点的挠度:f 2=f 0(1-m)=0.0237(1-0.086)=0.0055式中:f 0=[P 0/G ]f 1=[1412/2200]×0.03696=0.0237 m= f 0/e 0=0.0237/0.022=1.0773 e 0=0.1δ=0.1×0.22=0.022 11. 轴在b 点的总挠度f=f 1+f 2=0.02688+0.0055=0.0495 12. 挠度占气隙的百分数f ′=0.0495/0.7×100%=7.1% 13. 许用挠度[f ]=8%>7.1%,因此轴的挠度满足要求。
14. 转轴临界转速:n kp =200min /912044.0/)086.01(200/)1(1r f m =-=- (n kp -n N )/n N =(912-200)/200=356%>30%,因此轴的临界转速满足要求。
(二)、轴的疲劳强度的安全系数计算:轴的疲劳强度按轴上长期作用的最大变载荷进行计算,对同步电动机来说可按3倍的额定转矩来计算,轴的疲劳强度校核主要是长期受载荷作时危险截面的安全系数校核,具体计算如下: 1、轴系受力分布图轴系受力可按集中载荷考虑,受力如下图所示,其中G =38000Kg (按转子整个重量计算), 单边磁拉力P0=5153Kg,P0+G=43153Kg 。
一、临界转速分析的目的临界转速分析的主要目的在于确定转子支撑系统的临界转速,并按照经验或有关的技术规定,将这些临界转速调整,使其适当的远离机械的工作转速,以得到可靠的设计。
例如设计地面旋转机械时,如果工作转速低于其一阶临界转速Nc1,应使N<,如果工作转速高于一阶临界转速,应使<N<+1,而对于航空涡轮发动机,习惯做法是使其最大工作转速偏离转子一阶临界转速的10~20%。
二、选择临界转速计算方法要较为准确的确定出转子支撑系统的临界转速,必须注意以下两点1.所选择的计算方法的数学模型和边界条件要尽可能的符合系统的实际情况。
2.原始数据的(系统支撑的刚度系数和阻尼系数)准确度,也是影响计算结果准确度的重要因素。
3.适当的考虑计算速度,随着转子支撑系统的日益复杂,临界转速的计算工作量越来越大,因此选择计算方法的效率也是需要考虑的重要因素。
三、常用的计算方法注:斯托多拉法莫克来斯塔德法传递矩阵法基本原理:传递矩阵法的基本原理是,去不同的转速值,从转子支撑系统的一端开始,循环进行各轴段截面状态参数的逐段推算,直到满足另一端的边界条件。
优点:对于多支撑多元盘的转子系统,通过其特征值问题或通过建立运动微分方程的方法求解系统的临界转速和不平衡响应,矩阵的维数随着系统的自由度的增加而增加,计算量往往较大:采用传递矩阵法的优点是矩阵的维数不随系统的自由度的增加而增大,且各阶临界转速计算方法相同,便于程序实现,所需存储单元少,这就使得传递矩阵法成为解决转子动力学问题的一个快速而有效的方法。
缺点:求解高速大型转子的动力学问题时,有可能出现数值不稳定现象。
今年来提出的Riccati传递矩阵法,保留传递矩阵的所有优点,而且在数值上比较稳定,计算精度高,是一种比较理想的方法,但目前还没有普遍推广。
轴段划分:首先根据支撑系统中刚性支撑(轴承)的个数划分跨度。
在整个轴段内,凡是轴承、集中质量、轮盘、联轴器等所在位置,以及截面尺寸、材料有变化的地方都要划分为轴段截面。
轴的临界转速计算公式轴的临界转速也称为临界频率,是指转子在转动时出现横向振动的频率,达到一定的转速时会产生严重的振动破坏。
因此,对于设计和选择轴的转速有很重要的意义。
本文将介绍轴的临界转速计算公式,包括理论计算和实际测量方法。
一、理论计算方法轴的临界转速可以用理论计算方法来估算。
这种方法通常基于轴的自然频率和叶轮的惯性力。
我们可以根据叶轮的质量、惯性矩、叶轮与轴的连接方式等参数来计算出叶轮的振动特性,并根据轴的材料属性、截面形状和长度等参数来计算轴的自然频率。
然后,我们可以使用下面的公式来计算轴的临界转速:Ncr = Kcr / (π*D)其中,Ncr为轴的临界转速,单位为rpm;Kcr为轴的临界弯曲刚度,单位为N·m^2;D为轴的直径,单位为m。
这个公式基于轴的弯曲振动模式,假设轴由弹性材料制成且柔度均匀。
因此,由轴截面转换为转子刚度,可以得到下面的数学公式:Kcr = (2*π*fcr)^2 * I / L其中,fcr为轴的临界频率,单位为Hz;I为轴的截面转动惯量,单位为m^4;L为轴的长度,单位为m。
转子的质量和惯性矩均假定为分布均匀,因此I可以计算为轴的截面面积与离心力作用点到轴心的垂直距离之积。
对于均匀截面的圆形轴,其转动惯量计算公式为:I = π*r^4 / 4其中,r为轴半径。
对于矩形截面的轴,其转动惯量可以计算如下:I = bh^3 / 12其中,b为轴的宽度,h为轴的高度。
二、实际测量方法除了理论计算方法外,我们还可以使用实际测量方法来计算轴的临界转速。
这种方法通常涉及使用专用的振动测量仪器来确定轴的振动模式和频率。
在测量之前,我们需要保证轴处于静止状态和固定状态。
然后,我们可以使用如下步骤来进行实际测量:1、使用加速度传感器或振动传感器在轴的相对位置测量振动;2、在轴上施加导轮或质量块用于激起振动,然后记录振动测量结果;3、分析振动数据并确定轴的自然频率和振动模式;4、使用振动模态和自然频率计算轴的临界转速。