运筹学发展简史

中国运筹学会的简史和今日的发展“运筹”一词，出自中国《史记·高祖本记》：“夫运筹策帷幄之中，决胜于千里之外”。

运筹学的英文词Operational Research最早出现于1938年，原意为“作战研究”。

在美国称为Operations Research，英文缩写为OR。

20世纪50年代中期，钱学森、许国志等教授将运筹学引入我国，并结合我国的特点在国内推广应用，中国学术界将原词译为运筹学。

现代运筹学被引入中国是在五十年代后期。

中国第一个运筹学小组在钱学森、许国志先生的推动下在1956年于中国科学院力学研究所成立。

可见，运筹学一开始就被理解为同工程有密切联系的学科。

1959年，第二个运筹学部门在中国科学院数学研究所成立，这是大跃进中数学家们投身于国家建设的一个产物。

力学所小组与数学所的小组于1960年合并成为数学研究所的一个研究室，当时的主要研究方向为排队论、非线性规划和图论，还有人专门研究运输理论、动态规划和经济分析（例如投入产出方法）。

1963年是中国运筹学教育史上值得一提的一年，数学研究所的运筹学研究室为中国科技大学应用数学系的第一届毕业生（58届）开设了较为系统的运筹学专业课，这是第一次在中国的大学里开设运筹学专业和授课。

今天，运筹学的课程已变成所有大学的商学院、工学院乃至数学系和计算机系的基本课程了。

五十年代后期，运筹学在中国的应用集中在运输问题上，其中一个广为流传容易明白的例子就是“打麦场的选址问题”，目的在于解决当时手工收割为主的情况下如何节省人力和实践。

国际上大家都知道的“中国邮路问题”模型也是在那个时期由管梅谷教授提出的。

所以，现在非常热门的“物流学”，在当时就有一些雏形的研究，但可惜中国的大工业落后，又不是市场环境，使我们在相当长的时期中远离了当代“物流学”的发展主流。

中国运筹学早期应用的亮点是由华罗庚教授点燃的。

在文化大革命期间，身为中国数学会理事长和中科院院士的他，亲自率领一个小组，大家称为“华罗庚小分队”，到农村、工厂讲解基本的优化技术和统筹方法，使用于日常的生产和生活中。

一、绪论§1 运筹学的简史运筹学作为科学名称出现于20世纪30年代末。

英、美对付德国空袭，采用雷达，技术上可行，实际运用不好用。

如何合理运用雷达？“运用研究”（Operational Research）,我国1956年用“运用学”名词，1957年正式定名为运筹学。

运筹学小组在英、美军队中成立，研究：护航舰队保护商船队的编队问题、当船队遭受德国潜艇攻击时如何使船队损失最小问题、反潜深水炸弹的合理爆炸深度（德国潜艇被摧毁数增到400%）、船只在受敌机攻击时的逃避方法（大船急转向、小船缓转向，中弹数由47%降到29%）。

运筹学组织在英、美军队（RAND）中成立，研究：战略性问题、未来武器系统的设计和合理运用方法、美国空军各种轰炸机系统的评价、未来武器系统和未来战争战略、苏联军事能力及未来预报、苏联政治局计划的行动原则和未来战争的战略、到底发展哪种洲际导弹（50年代）、战略力量的构成和数量（60年代）。

运筹学在工业、农业、经济、社会问题等领域有应用。

运筹数学：数学规划（线性规划（丹捷格（G.B.Dantzig）1947，单纯形法；康托洛维奇1939解乘数法，1960《最佳资源利用的经济计算》，诺贝尔奖；列昂节夫1932投入产出模型；冯.诺意曼）、非线性规划、整数规划、目标规则、动态规划、随机规划等）、图论与网络、排队论（随机服务系统理论）(丹麦工程师爱尔朗（Erlang）1917提出一些著名公式)、存贮论、对策论（冯.诺意曼和摩根斯坦，1944《对策论与经济行为》）、决策论、维修更新理论、搜索论、可靠性和质量管理等。

运筹学领域的诺贝尔奖得主：阿罗、萨谬尔逊、西蒙（经济学家）、多夫曼、胡尔威茨、勃拉凯特（Blackett,美，物理学家）。

运筹学会的建立：英国（1948年）、美国（1952年）、法国（1956年）、日本（1957年）、印度（1957年）、中国（1980年），38个国家和地区。

国际运筹学联合会（IFORS）的成立：1959年，英、美、法发起成立，中国1982年加入。

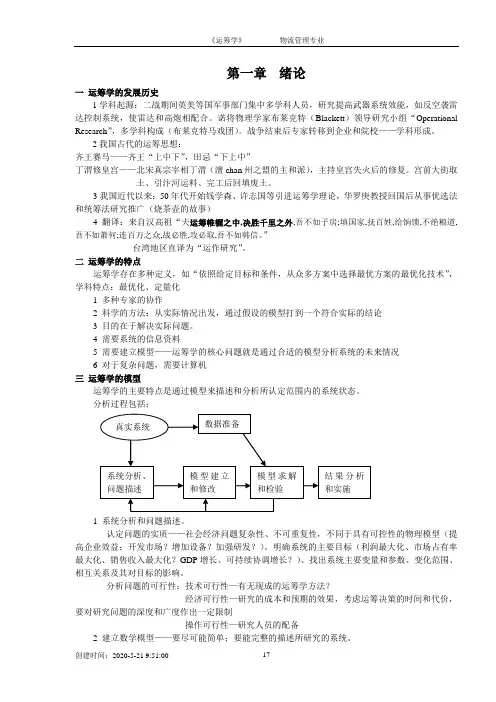
第一章绪论一运筹学的发展历史1学科起源：二战期间英美等国军事部门集中多学科人员，研究提高武器系统效能，如反空袭雷达控制系统，使雷达和高炮相配合。

诺将物理学家布莱克特（Blackett）领导研究小组“Operational Research”，多学科构成（布莱克特马戏团）。

战争结束后专家转移到企业和院校——学科形成。

2我国古代的运筹思想：齐王赛马——齐王“上中下”，田忌“下上中”丁渭修皇宫——北宋真宗宰相丁渭（澶chan州之盟的主和派），主持皇宫失火后的修复。

宫前大街取土、引汴河运料、完工后回填废土。

3我国近代以来：50年代开始钱学森、许志国等引进运筹学理论，华罗庚教授回国后从事优选法和统筹法研究推广（烧茶壶的故事）4翻译：来自汉高祖“夫运筹帷幄之中,决胜千里之外,吾不如子房;填国家,抚百姓,给饷馈,不绝粮道,吾不如萧何;连百万之众,战必胜,攻必取,吾不如韩信。

”台湾地区直译为“运作研究”。

二运筹学的特点运筹学存在多种定义，如“依照给定目标和条件，从众多方案中选择最优方案的最优化技术”，学科特点：最优化、定量化1 多种专家的协作2 科学的方法：从实际情况出发，通过假设的模型打到一个符合实际的结论3 目的在于解决实际问题。

4 需要系统的信息资料5 需要建立模型——运筹学的核心问题就是通过合适的模型分析系统的未来情况6 对于复杂问题，需要计算机三运筹学的模型运筹学的主要特点是通过模型来描述和分析所认定范围内的系统状态。

分析过程包括：1 系统分析和问题描述。

认定问题的实质——社会经济问题复杂性、不可重复性，不同于具有可控性的物理模型（提高企业效益：开发市场？增加设备？加强研发？）。

明确系统的主要目标（利润最大化、市场占有率最大化、销售收入最大化？GDP增长、可持续协调增长？）、找出系统主要变量和参数、变化范围、相互关系及其对目标的影响。

分析问题的可行性：技术可行性—有无现成的运筹学方法？经济可行性—研究的成本和预期的效果，考虑运筹决策的时间和代价，要对研究问题的深度和广度作出一定限制操作可行性—研究人员的配备2 建立数学模型——要尽可能简单；要能完整的描述所研究的系统。

第一章绪论1 运筹学简史运筹学（Operations Research）(or Operational Research)是交通运输管理专业所必修的一门主干课程，也是其它管理专业的必修课，是许多其它专业的基础课。

在现代化的管理中，运筹学正起着日益重要的作用。

运筹学这门新兴的学科是第二次世界大战期间在英国首先出现的当时雷达刚刚发明，但是在开始使用时却不能很好地和高炮配合，为了帮助参谋人员研究新的反空袭雷达控制系统，1940年8月在得过诺贝尔奖金的物理学家布莱克特（P.M.S.Blackett）教授领导下建立了一个研究小组。

这个特殊的小组第一次应用了Operational Research这个名词意思是军事活动研究，称为“运用研究”。

当时这个小组包括物理学家、数学家、生理学家、天文学家、军官等人。

研究工作从空军扩展到海军和陆军。

不久，美国也建立了类似的小组并称之为Operations Research。

这些专门小组开展了护航舰队保护商船队的编队问题和当船队遭受德国潜艇攻击时，如何使船队损失最少的问题的研究（即商船护航、反潜艇研究）。

通过研究反潜深水炸弹的合理爆炸深度后，使德国潜艇被摧毁数增加到400%；研究了船只在受敌机攻击时，提出了大船应急转向和小船缓慢转向的逃避方法。

研究结果使船只在受敌机攻击时，中弹数由47%降到29%。

当时研究和解决的问题都是短期的和战术性的。

二战后，在英、美军队中相继成立了更为正式的运筹研究组织，并以兰德(Rand)公司为首的一些部门开始着重研究战略性问题；研究未来的武器系统的设计和其可能合理运用的方法。

例如美国空军评价各种轰炸机系统讨论未来的武器系统和未来战争的战略。

他们还研究了苏联军事能力及未来的预报，分析苏联的政治局计划的行动原则和将来的行动预测。

到了50年代，由于开发了各种洲际导弹，到底发展那种，运筹学界也投入了研究。

到了60年代，运筹学除了在军事方面应用研究外，开始了在工业、农业、经济和社会问题等各领域都开始了应用。

运筹学的概念运筹学是一种综合性学科，它在现代管理中起着至关重要的作用。

运筹学是一种运用数学、统计学、计算机科学以及其他相关领域的方法和理论来帮助制定最优决策的学科。

它的主要目标是通过通过信息分析和决策模型来使决策者在制定决策时更加合理、科学和精准。

下面是对运筹学概念的详细介绍。

一、运筹学的基本定义运筹学（Operations Research，简称OR）是一门科学，通过使用计算机和数学模型，研究如何最好地利用有限资源来达到预期目标，主要研究方法包括优化、数理统计、决策分析、模拟等。

二、运筹学的发展历程运筹学是在二战期间发展出来的，主要应用于军事后勤问题的解决。

之后，运筹学学科马不停蹄地在各个领域快速发展，至今已经成为了一门广泛的学科。

三、运筹学的应用范围运筹学在各个领域都有广泛的应用，例如生产制造、物流管理、金融风险管理、医疗管理、资源分配等。

它在实践中的应用能够使企业和组织在有限的资源下获得最大收益。

例如，电商企业可以利用运筹学和网络优化技术来解决配送问题。

医院可以利用运筹学与供应链的整合优化来提高采购成本的效率。

银行等金融机构则可以利用运筹学来建立风险管理模型，减轻市场波动造成的经济损失。

四、运筹学的关键技术该学科主要基于优化、数学建模、统计推断和计算机仿真等关键技术。

对于不同的问题，会采用不同的技术手段。

例如，对于线性规划问题，使用线性规划算法进行求解；对于决策树问题，可以使用决策树算法进行求解；对于复杂的大规模问题，可以使用数学建模与计算机仿真技术进行求解。

总之，运筹学是为了解决实际问题而产生的一种学科，它在生产、经济、政策等许多领域有广泛应用，发展迅速，使得成本降低、管理规范化、业务流程优化等问题得到了解决。

运筹学基本概念与发展简介运筹学，又被称为管理科学，是一门综合应用数学、统计学以及其他相关学科的学科。

它的主要目标是通过系统化分析、建模和优化，在资源有限的情况下，达到最优的决策和解决问题的方法。

本文将对运筹学的基本概念和其发展历程进行简要介绍。

一、运筹学的基本概念运筹学的研究对象是各类决策问题，其核心思想在于如何通过适当的方法和技术，对复杂的系统进行优化。

具体而言，运筹学侧重于以下几个方面的内容：1. 数学模型建立：在解决问题之前，必须先建立适当的数学模型。

这些模型可以是线性规划、整数规划、图论、排队论等等。

2. 算法设计与优化：在建立数学模型之后，需要设计算法来求解模型。

算法设计的目标是提高计算效率和准确性。

3. 决策分析：传统的决策往往是依靠主观经验和直觉，而运筹学正是通过系统性的分析和决策模型，使决策过程具有量化、科学性和合理性。

4. 信息管理与决策支持系统：通过信息的获取、存储、处理和分析，提供可靠的支持和决策辅助。

二、运筹学的发展历程运筹学的发展可以追溯到20世纪40年代末期，当时运筹学主要应用于军事领域。

以美国作为代表的国家，大量运筹学家为战争中的资源分配、军事运输、作战计划等问题提供了有效的解决方案。

随着二战的结束，运筹学逐渐应用于工业管理和商业决策领域。

在20世纪50年代，随着计算机技术的进一步发展，运筹学得以迅速扩展。

线性规划、整数规划等方法的诞生，为企业的生产、销售、采购等问题提供了科学的决策支持。

到了1960-1970年代，运筹学领域又得到了新的发展。

传统的运筹学方法逐渐不能满足复杂决策问题的需求，因此出现了非线性规划、动态规划、随机规划等更加高级的方法。

随着信息技术的飞速发展，运筹学又迎来了新的机遇和挑战。

决策支持系统、智能算法等新兴技术的引入，使得运筹学得以更好地应用于实际生产和管理中。

三、运筹学的应用领域运筹学作为一门综合性的学科，应用广泛。

以下是运筹学的一些典型应用领域：1. 供应链管理：通过优化供应链中的各个环节，实现高效的物流运输、仓储管理和库存控制，从而降低成本、提高服务水平。

运筹学的发展历程
运筹学是一门应用数学学科，涉及系统设计、模型构建、优化算法、风险评估和决策分析等方面。

其发展历程可以追溯到二战期间，当时军队需要运用数学优化方法提高武器装备效率。

随着计算机技术的发展，运筹学逐渐得到推广和应用。

20世纪40年代初，英国的麦凯洛克和美国的丰特姆等学者开始从事运筹学的研究，提出了线性规划、瓶颈问题、输运问题等模型。

他们将运筹学应用于军事方面，使得美军能够更加高效地战斗。

20世纪50年代，由乔治·丹泽及其团队开发出的“SIMSCRIPT”系统运用了模拟技术，使得工业系统的规划和控制更加精确、高效。

20世纪60年代，运筹学的思想逐渐向民间领域推广，特别是交通运输领域。

由达顿等人开发的“DATANET”系统使工业企业的生产流程更加高效，提高了工业生产的效率。

20世纪70年代，与计算机的高速发展一起，运筹学逐渐成为一门独立的学科。

线性规划、非线性规划以及动态规划等多种解决优化问题的算法被建立。

与此同时，运筹学在管理科学和经济学领域得到广
泛应用。

管理科学领域更是开发了生产管理、项目管理、财务管理、决策管理等多个领域。

20世纪80年代，博弈论、组合优化、不确定性优化等新的分支学科开始蓬勃发展。

运筹学开始关注具有随机元素的不确定性问题。

计算机模拟技术、群体智能算法等新兴技术的应用也为运筹学发展带来了新的思路。

21世纪以来，运筹学的思想得到全球范围内广泛应用，公司、政府、学术机构及科研人员都致力于运筹学的研究和应用，为各领域提供了大量的优化方案和决策支持。

在计算机技术日新月异的时代，运筹学想必会有更加广泛的应用前景。

中国运筹学发展史运筹学是一门应用数学和形式科学来研究如何在有限资源下做出最优决策的科学。

自20世纪50年代以来，运筹学在中国得到了广泛的应用和发展。

本文将详细介绍中国运筹学的发展历程和重要成果。

一、起步阶段（1950-1960年）在20世纪50年代，随着中国的第一个五年计划的实施，运筹学开始在中国得到应用。

这个时期的重要事件包括1957年成立的北京大学数学力学系运筹学研究室，以及1958年成立的清华大学运筹学研究室。

这两个研究室的成立标志着中国运筹学的起步。

二、发展阶段（1960-1980年）在20世纪60年代和70年代，中国运筹学得到了进一步的发展。

这个时期的重要事件包括1961年成立的上海交通大学运筹学研究室，以及1978年成立的中国人民大学运筹学研究所。

这些研究机构的出现为中国运筹学的发展提供了重要的平台。

在这个阶段，中国运筹学在多个领域取得了重要的成果。

例如，在交通运输方面，运筹学被应用于铁路运输规划、公路运输网络优化等领域，取得了显著的成果。

在生产管理方面，运筹学被应用于生产流程优化、库存管理等领域，有效地提高了生产效率。

三、推广和应用阶段（1980-至今）自20世纪80年代以来，中国运筹学得到了广泛的推广和应用。

这个时期的重要事件包括1980年成立的全国运筹学会第一届理事会，以及1986年成立的中国科学院管理科学研究所。

这些机构的成立为中国运筹学的推广和应用提供了重要的支持。

在这个阶段，中国运筹学在各个领域都取得了显著的成果。

例如，在经济发展方面，运筹学被应用于宏观经济政策分析、产业结构优化等领域，为政府决策提供了重要的参考。

在军事领域，运筹学被应用于作战指挥、后勤保障等领域，提高了军队的作战能力。

此外，运筹学还被广泛应用于交通、能源、环境等领域的优化问题，为我国的可持续发展做出了贡献。

四、总结中国运筹学在近几十年的发展中取得了显著的进步，从起步阶段逐渐发展成为一门成熟的应用科学。

在发展过程中，中国运筹学不断汲取国内外先进理论和方法，形成了具有中国特色的研究体系。

运筹学发展史运筹学是集数学、统计学、经济学、计算机科学等多门学科于一体，研究各种决策问题的交叉学科。

自从人类有意识地制定计划以来，运筹学的思想就一直存在，但真正发展起来确切的时间起讫点却没有统一的说法。

下面简单地概述一下运筹学的发展史。

一、古代运筹学运筹学最早可以追溯到4,000年前的古埃及，当时人们利用图形技术，将土地、谷仓、士兵、财富等重要信息用图形表示出来，用以辅助管理和决策。

此后，古希腊和古罗马亦有类似的图形分析和辅助决策方法应用于军事和城市管理。

二、工业革命前的运筹学到了18世纪，活泼的商业活动迫切需要科学方法论的决策支持。

在这种背景下，经济学家列昂·瓦尔拉斯和庇古等先后提出了最大效用原则和社会福利函数，构建了古典政治经济学体系。

同时，机械制造工业的崛起也随之带动了计算机技术和管理学的不断发展。

三、第一次世界大战以后的运筹学到了20世纪初，经济学家弗兰克·兰姆述在他的《伯莱兹梅思思路: 经济思想的数学化》一书中首次提出了"经济数学"和"统计经济学"这两个术语.此后一段时间内，许多重要的数学工具和技术被逐步引入到决策支持系统技术中，并被运用在如港口货物装卸优化问题、城市交通问题等实际工程中。

进入第二次世界大战，大型的军事行动对后勤保障的要求更加凸显，运筹学技术被大量运用到物资的调配、运输的规划等各个方面。

比如，著名的杜伯敦庞加莱攻略，利用运筹学思想，通过规范的运输和调度方式，提高了军队装备的配送效率，保障了军队的胜利。

之后，运筹学逐渐扩展至更多领域，尤其是工业、交通等部门的运作和管理领域，成为国家级决策和项目管理的核心内容。

进入21世纪后，数据信息技术的飞速发展和智能化技术的不断涌现，为运筹学技术的发展提供了新的契机。

数学工具、建模方法、优化算法、分析技术等都得到了大幅度的改进和完善，应用范围更广，支持更加高效。

运筹学已成为决策管理领域的一项重要技术，为企业管理、产业流程、政策决策等方面带来了显著的效益和实践价值。

运筹学的发展历程概述运筹学是一门研究如何在有限资源下做出最佳决策的学科，它涵盖了数学、统计学、经济学和管理学等多个领域。

本文将对运筹学的发展历程进行全面详细的介绍。

古代运筹运筹学的起源可以追溯到古代。

在中国，古代军事家孙子就提出了一些与运筹相关的思想，他在《孙子兵法》中强调了军队应该根据敌情和自身条件进行灵活调整和优化，以取得最佳战果。

此外，古希腊数学家欧几里德也提出了一些与最优化相关的几何问题。

数学规划的诞生20世纪上半叶，随着数学和计算机科学的快速发展，运筹学开始成为一个独立的研究领域。

1947年，美国数学家乔治·邓鲁克（George Dantzig）提出了线性规划问题的解法——单纯形法。

这一方法基于线性规划模型，通过迭代求解单纯形表来寻找最优解。

邓鲁克的工作奠定了数学规划的基础，并为运筹学的发展打下了坚实的基础。

运输和网络优化20世纪50年代和60年代，运输和网络优化成为运筹学研究的热点。

研究者开始关注如何在给定资源限制下优化物流和交通网络。

1956年，美国数学家乌拉姆（Stanislaw Ulam）提出了著名的旅行商问题（Traveling Salesman Problem），该问题要求找到一条最短路径经过所有城市并返回起点。

这一问题成为了运筹学中一个重要的组合优化问题。

随机模型和决策分析20世纪60年代，随机模型和决策分析开始在运筹学中发挥重要作用。

随机模型考虑到不确定性因素对决策结果的影响，通过概率论和统计学方法进行建模和分析。

决策分析则着眼于如何在不确定环境下做出最佳决策。

这些方法对于管理科学和工程领域具有重要意义。

多目标规划与非线性规划20世纪70年代，多目标规划和非线性规划成为运筹学的新研究方向。

多目标规划考虑到多个冲突目标之间的权衡和平衡，寻找一个最优解集合。

非线性规划则研究非线性约束条件下的最优解问题，这种问题在实际应用中非常普遍。

进一步发展与应用随着计算机技术的不断进步，运筹学在实践中得到了广泛应用。

运筹学讲稿一、运筹学的简史运筹学的早期工作及其历史可追溯到1914年，当时兰彻斯特（Lanchester）提出了军事运筹学的战斗方程；1917年，丹麦工程师埃尔朗（Erlang）在哥本哈根电话公司研究电话通信系统时，提出了排对论的一些著名公式；20世纪20年代初提出了存储论的最优批量公式.1947年美国数学家丹西格（G..B.Danting）在解决美国空军军事规划问题时，提出了线性规划及单纯形法.早在1939年，前苏联学者康托洛维奇（JT.B.KaHTopobny）在解决工业生产组织和计划问题时，已提出了类似线性规划模型，并给出了“解乘数法”的求解法.可惜当时未被重视.运筹学作为一门科学诞生于20世纪30年代末期，通常认为运筹学的活动是第二次世界大战早期从军事部门开始的.当时，英国为了研究“如何最好的运用空军及新发明的雷达保卫国家”，成立了一个由各方面的专家组成的交叉学科小组，即最早的运筹小组.进行“作战研究”（Operational,research），后来中文译名为“运筹学”.（我国在1956年用过运用学的名词，到1957年正式定名为运筹学）.第二次世界大战期间，英、美军队中的运筹学小组研究诸如护航舰队保护商对的编队问题；当船队遭受德国潜艇的攻击时，如何使船队损失最小的问题，反潜深水炸弹的合理起爆深度问题；稀有资源在军队中的分配问题等.第二次世界大战后，特别是运筹学在军事上的显著成功，引起了人们的广泛的关注，运筹学很快深入到工业、商业、政府部门等，并得到了迅速发展.在20世纪50年代中期，钱学森、许国志等老教授全面介绍运筹学，并结合我国特点在国内推广应用.1957年，我国在建筑业和纺织业中首先应用运筹学；从1958年开始在交通运输、工业、农业、水利建设、邮电等方面陆续得到推广应用.在解决邮递员合理投递线路时，管梅谷教授提出了国外称之为“中国邮路问题”的解法；从20世纪60年代起，运筹学在钢铁和石油部门开始得到了比较全面、深入的应用.从1965年起，统筹学法在建筑业和大型设备维修计划等方面的应用取得了可喜的进展；1970年在全国大部分省、市和部门推广优选法；70年代中期，最优化方法在工程设计界受到了广泛的重视，并在许多方面取得成果；排队论开始应用于矿山、港口、电信及计算机等方面；图论用于线路布置、计算机设计、化学物品的存放等；70年代后期,存储论在应用汽车工业等方面获得成功.在此期间，以华罗庚教授为首的一大批数学家加入到运筹学的研究队伍，使运筹学的很多分支很快跟上当时的国际水平.运筹学是一门应用科学，至今还没有统一且确切的定义. 参见：程理民《运筹学模型与方法教程》 钱颂迪主编《运筹学》，清华大学出版二、引例例1 某工厂生产甲、乙两种产品，生产每件产品需要原材料、能源消耗、劳动力及所获利如下表所示：现有库存原材料1400千克；能源消耗总额不超过2400百元；全厂劳动满员为2000人，试安排生产任务（生产甲、乙产品各多少件），使获得利润最大，并求出最大利润. [模型建立]设安排生产甲产品x 件，乙产品y 件，相应的利润为S ,则此问题的数学模型为：maxS=5x+6y s.t. 2x+3y ≦1400x+6y ≦2400 (1) 4x+2y ≦2000 x ≥0,y ≥0,x,y ∈Z这是一个整数线性规划问题.例2 某工厂有100台机器，拟分四期使用，在每一期中有生产任务1A ，2A 两种.设第k 个周期初有完好的机器k x 台，根据经验，若周期初把k u 、k x -k u 台机器分别投入任务1A ，2A ，则周期末分别有k u /3、k x -k u /10台机器作废（k=1，2，3，4），如果在一个生产周期中每一台机器执行任务1A 可收益10千元，执行任务2A 可收益7千元，问怎样分配机器使收益最大？试建立数学模型.[数学模型的建立] 按题设，k x ，k u （k=1、2、3、4）受约束于(subject to 简记为 s.t.）1+k x =32k u +109(k x -k u ),0≤k u ≤k x 且1x =100 第K 个周期收益10k u +7（k x -k u ），因此四个周期的总收益为 V=∑=41k （10k u +7（k x -k u ）），于是问题的数学模型为：Max V=∑=41k （10k u +7(k x -k u ））s.t. 1+k x =32k u +109(k x -k u ) (2) 0≤k u ≤k x 且1x =100 ， k=1,2,3,4 这是一个分步决策，且为线性规划问题.例3 某投资者有5亿元，想取其中的一部分对项目1A ，2A 进行投资，设投资i x 亿元项目i A ,从历史资料来分析，投资于项目1A 和2A 分别有预期的年收益20%和16%.同时，与项目1A 和2A 有关的总的风险损失为2212221)(2x x x x +++ (记为Q) .试设计使预期的总收益R 最大而风险损失Q 尽可能的小的投资方案. [数学模型]此问题的数学模型为： Max R=0.21x +0.162x Min Q=2212221)(2x x x x +++ (3)s.t 21x x +≦5, 21,x x ≧0注意到：Min Q=Max(-Q),若投资者根据总收益与风险损失对自己的重要程度确定权系数，希望f=0.8R+0.2(-Q)最大，则数学模型为Max f=0.8(0.21x +0.162x )-0.2[2212221)(2x x x x +++] s.t 21x x +≦5, 21,x x ≧0 (4)三、数学模型的基本概念及解法1、概念① 在上面的数学模型（1）--（4）中，都是求函数的极值问题，象这样的在等式或不等式约束条件下求一元或多元函数的极值问题，称为数学规划问题.这个需要求极值的函数称为目标函数.数学规划问题中的自变量称为决策变量.② 在数学规划中，目标函数和约束条件中的函数式都是线性的，就称它为线性规划问题.否则就称非线性规划问题（至少有一个非线性的）. 如（1）（2）是线性规划；（4）是非线性规划.③ 早在1939年前苏联数学家康托洛维奇（JT.B.KaHTopobny ）和美国的希奇柯克（F.Litchcock ）等人就在生产组织管理和制定交通运输方案方面首先研究了和运用了线性规划方法.1947年，美国数学家丹西格（G..B.Danting ）提出了单纯行法，给出了求线性规划的上实用方法.④ 对于例3，数学规划（3）：在此数学规划问题中目标函数有多个，就称它为多目标规划问题.例如，全国大学生数学建模竞赛题96年A 题、98年A 题、98年B 题、03年B 题等都是多目标函数规划问题.⑤ 另外，目标函数，约束条件，出现“最多约能”；“约不能超过”.这种模糊概念、若至少出现一个，则就称相应的规划为模糊（数学）规划问题.⑥ 又如在(4)中，数学规划问题中，目标函数为二次函数，且约束条件中的函数式子是线性的，则称它为二次规划. ⑦线性规划的一般形式为∑==nj j j x c Z 1mins.t.()()()n j x b a x a b x a x a j m mn m n n,2,1.01111111=≥≥≤+≥≤++其中j i ij c b a ,,均为已知常数.矩阵表示:()0..min ≥≥≤=X b b AX t s CX Z 或⑧标准形式(矩阵)为..min ≥≤=X b AX t s CX Z (松弛度量,剩余度量)⑨线性规划问题中满足约束条件的解称为可行解,其全体称为可行域,使目标函数达到最小值(最大值)的可行解称为最优解,最优解对应的目标函数值勤称为最优值. 最优解为0X ,最优值为0CX . 2.重要结论 ① 若线性规划问题⑸存在可行域,则可行域为凸集.②若线性规划问题可行域有界，则最优解在可行域的顶点达到.3．数学规划的解法； ①． 解线性规划的单纯形法，（解法一）. ②．解法二 lindo 数学软件.Lindo ()()⎪⎪⎩⎪⎪⎨⎧.2.30,,50,100,200,,解线性非线性整数规划解线性整数规划个约束个变量解非线性规划个约束个变量二次规划线性规划Lingo lingo Gind lindo安装 A ：>install ↓ C: > . ；(表示进入状态) 例如 求 y x Z 32max +=s.t. 0.12531034≥≤+≤+y x y x y x.32max y x +? S T (或S.T 或Subject to) ? 1034<+y x ? 1253<+y x ? END : 运行 Go③． 图解法（线性规划）求例的数学模型.可行域为由；y x y x l by x l y x l 组成的凸五边形区域及.0,0.200024:,2400:,140032:321===+=+=+ 直线。