销售按地区占比统计图表

竭诚为您提供优质文档/双击可除excel月销售统计表格篇一：20xx等级考试excel(60套)1.（图表，计算，数据表）2.（图表及格式设置，计算）4.（自动筛选，排序，计算，格式设置）5.（图表及格式设置，计算）6.（图表及格式设置，计算）7.（计算，图表）8.（计算，图表）9.（图表及格式设置，计算）10.（max和min，套用表格格式，图表）11.（iF，表格套用，排序，自动筛选，平均）12.（Rank函数，图表，图表格式设置，计算，排序，）13.（计算，图表及格式，自动筛选）15.（计算，条件格式，套用格式，自动筛选（同13））16.（计算，图表）17.（计算，Rank，排序，套用格式，图表格式）18.（排名，Rank，iF，and，分类汇总）19．（max，条件格式，图表，排序，自动筛选）20.（iF，条件格式，图表，排序，自动筛选）21.（计算，mode，套用格式，图表，自动筛选）22.（countiF，图形，透视表）23.（countiF，图表，透视表）24.（计算，iF，图表，排序，高级筛选）25.（max，图表，排序，高级筛选）26.（计算，图表）27.（计算，图表，分类汇总）28.（计算，图表，高级筛选，排序）29.（计算，Rank，条件格式，图表，自动筛选）30.（计算，countiF，图表，数据透视表）31.（计算，图表，排序，分类汇总）32.（条件格式，图表，图表样式，排序，分类汇总）33．（计算，iF，单元格样式，图表及样式，数据透视表）34.（计算，iF，条件格式，图表，透视表）35.（计算，max，套用格式，图表，排序，分类汇总）36.（计算，表格套用格式，图表，排序，高级筛选）37.（计算，Rank，条件格式，图表，数据透视表）38.（计算，iF，表格套用格式，图表，高级筛选）39.（计算，样式，条件格式，图表，自动筛选）40.（计算，Rank，条件格式，图表，自动筛选）41.（计算，样式，条件格式，图表，自动筛选）42.（计算，条件格式，图表，自动筛选）43.（Rank，条件格式，图表，排序）44.（计算，条件格式，图表，排序）45.（计算，图表，自动筛选）46.（计算，图表，分类汇总，排序）47.（计算，图形，自动筛选）48.（计算，复制图表，图形，排序）49.（计算，图表，分类汇总）50.（计算，图表，排序，汇总）51.（计算，图表，自动筛选）52.（计算，Rank，条件格式，图表，自动筛选）53（筛选，计算，Rank，套用格式，图表，自动筛选，排序.54.（计算，countiF，图表，透视表）55.（计算，countiF，sumFi，图表，自动筛选）56.（countiF，sumiF，套用表格格式，图表，自动筛选）57.（计算，Rank，套用表格格式，图表，筛选，排序）58.（计算，max，图表，排序，分类汇总）59.（计算，Rank，条件格式，图表，筛选，排序）60.（计算，iF，图表，排序，汇总）精华题1（建立数据表，格式设置，计算）．精华题2（排序，汇总，透视表）．精华题3．(筛选)精华题4．（mode,if,rank）精华题5．（图表）1.（图表，计算，数据表）(1)打开工作簿文件table.xlsx，将下列数据建成一个数据表(存放在a1:e5的区域内)，并求出个人工资的浮动额以及原来工资和浮动额的"总计"（保留小数点后面两位），其计算公式是：浮动额=原来工资×浮动率，其数据表保存在sheet1工作表中。

五、电子表格题【试题一】1、打开考生文件夹下工作簿文件EXCEL.XLS，将下列数据建成一个数据表（存放在A1：E5的区域内），并求出“上升案例数”（保留小数点两位），其计算公式是：上升案例数=去年案例数×上升比率，其数据表保存在sheer1 1 工作表中。

序号地区去年案例数上升比率上升案例数1 A地区2400 1.00%2 B地区5300 0.50%3 C地区8007 2.00%4 D地区3400 2.10%2、对建立的数据表选择“地区”、“上升案例数”两列数据建立“分离型三维饼图”，系列产生在“列”，图表标题为“地区案例上升情况调查图”，并将其嵌入到工作表的A7：E17区域中。

3、将工作表sheet1更名为“案例调查表”【试题二】1、在考生文件夹下打开EXCEL.XLS文件：（1）将aheet1工作表的A1:D1单元格合并为一个单元格，内容水平居中；计算员工的“平均年龄”置D13单元格内（数值型，保留小数点后1位）；计算学历为本科、硕士、博士的人数置F5:F7单元格区域（利用COUNTIF函数）。

（2）选取“学历”列（E4:E7）和“人数”列（F4:F7）数据区域的内容建立“条形圆柱图”（系列产生在“列”），图表标题为“员工学历情况统计图”，图列位置靠上，设置数据系列格式图案内部背景颜色为淡蓝色；将图插入到表的A15:F28单元格区域内，将工作表命名为“员工学历情况统计表”，保存EXCEL.XLS文件。

2、打开工作薄文件EXL.XLS，对工作表“产品销售情况表”内数据清单的内容建立数据透视表，按行为“产品名称”，列为：“季度”，数据为“销售额（万元）”求和布局，并置于现工作表的I5:M10单元格区域，工作表名不变，保存EXL.XLS工作薄。

【试题三】1、在考生文件夹下打开EXC.XLS，将sheet1工作表的A1:E1单元格合并为一个单元格，水平对齐方式设置为居中；计算各位员工工资的税前合计（税前合计=基本工资+岗位津贴-扣除杂费），将工作表命名为“员工工资情况表”。

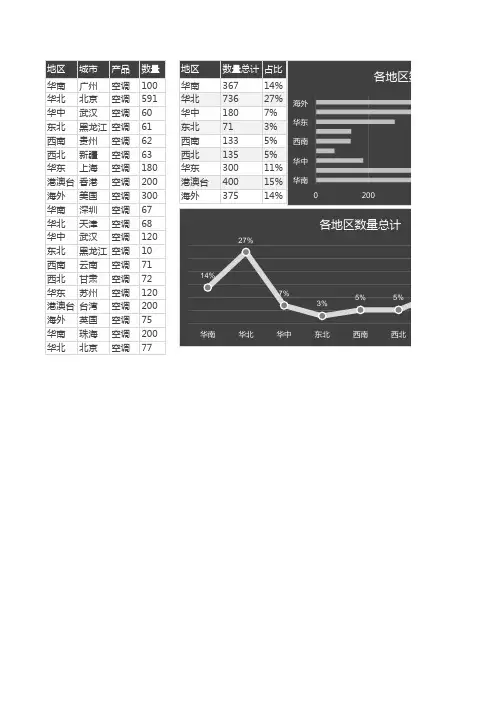
报告中的饼状图与条形图应用简介：在现代社会，数据和报告在我们日常工作和生活中扮演着重要的角色。

为了更加清晰地展示数据和统计结果，我们使用了各种图表和图形。

在本文中，我们将讨论报告中饼状图和条形图的应用，并探索这两种图表形式在不同领域中的优势和局限性。

一、饼状图的应用1.1 饼状图的概念和特点饼状图是一种以“饼”形式展示数据分布的图表。

它将整体数据按比例划分为不同的扇形，并使用不同的颜色或图例标注每个扇形代表的数据部分。

饼状图最常用于展示百分比或比例数据，特别是在展示总体占比方面非常有效。

1.2 饼状图的应用场景饼状图广泛应用于市场调研报告、金融和经济报告、人口统计数据报告等领域。

在这些领域中，饼状图能够清楚地展示不同项目或因素的相对比例。

例如，市场调研公司可以使用饼状图展示不同产品的市场占有率，从而帮助企业决策；经济学家可以使用饼状图展示国家各行业的经济构成，有助于分析经济结构和趋势。

1.3 饼状图的优势和局限性饼状图的优势在于它能够直观地展示数据的比例关系，使读者一目了然。

同时，饼状图还可以通过调整颜色和图例以及添加标签等方式增强可读性。

然而，饼状图也存在一定的局限性。

它不能展示大量数据，因为饼状图过于复杂会导致视觉混乱。

此外，饼状图无法展示数据的顺序或排名，也无法有效比较饼状图的扇形大小，因为人的视觉对于弧度和面积的判断相对不准确。

二、条形图的应用2.1 条形图的概念和特点条形图是一种以长方形条形的高度和长度来表示不同项目的数据大小，通过不同的颜色或阴影区分不同项目。

条形图常被用于展示分类数据，它能够清晰地显示各项目之间的差异和变化趋势。

2.2 条形图的应用场景条形图被广泛应用于各个领域。

在市场营销报告中，条形图通常用于展示不同产品的销售额或市场份额。

在健康领域，条形图可用于比较不同国家的健康指标，帮助医疗机构和决策者识别问题和解决方案。

此外，条形图还可以用于在教育和研究领域展示学生或研究对象的评估结果，帮助评估和改进教学和研究方法。

热点专题3 图表信息问题考向1平均数、中位数、众数、方差的概念及计算1.(2019 江苏省常州市)在“慈善一日捐”活动中，为了解某校学生的捐款情况，抽样调查了该校部分学生的捐款数（单位：元），并绘制成下面的统计图．（1）本次调查的样本容量是，这组数据的众数为元；（2）求这组数据的平均数；（3）该校共有600名学生参与捐款，请你估计该校学生的捐款总数．【答案】（1）30，10（2）12；（3）7200【解析】（1）本次调查的样本容量是6+11+8+5＝30，这组数据的众数为10元；故答案为：30，10；（2）这组数据的平均数为＝12（元）；（3）估计该校学生的捐款总数为600×12＝7200（元）．点评此题考查的是条形统计图的综合运用．读懂统计图，从统计图中得到必要的信息是解决问题的关键．条形统计图能清楚地表示出每个项目的数据．本题也考查了平均数、中位数、众数的定义以及利用样本估计总体的思想．2. (2019 江苏省南京市)如图是某市连续5天的天气情况．（1）利用方差判断该市这5天的日最高气温波动大还是日最低气温波动大；（2）根据如图提供的信息，请再写出两个不同类型的结论．【解析】（1）方差：一组数据中各数据与它们的平均数的差的平方的平均数，叫做这组数据的方差；（2）用“先平均，再求差，然后平方，最后再平均”得到的结果表示一组数据偏离平均值的情况，这个结果叫方差，通常用s2来表示，计算公式是：s2＝[（x1﹣）2+（x2﹣）2+…+（x n﹣）2]（可简单记忆为“方差等于差方的平均数”）．解答解：（1）这5天的日最高气温和日最低气温的平均数分别是＝＝24，＝＝18，方差分别是＝＝0.8，＝＝8.8，∴＜，∴该市这5天的日最低气温波动大；（2）25日、26日、27日的天气依次为大雨、中雨、晴，空气质量依次良、优、优，说明下雨后空气质量改善了．【点评】本题考查了方差，正确理解方差的意义是解题的关键．方差是反映一组数据的波动大小的一个量．方差越大，则平均值的离散程度越大，稳定性也越小；反之，则它与其平均值的离散程度越小，稳定性越好．3. (2019 江苏省淮安市)某企业为了解员工安全生产知识掌握情况，随机抽取了部分员工进行安全生产知识测试，测试试卷满分100分．测试成绩按A、B、C、D四个等级进行统计，并将统计结果绘制了如下两幅不完整的统计图．（说明：测试成绩取整数，A级：90分～100分；B级：75分～89分；C级：60分～74分；D级：60分以下）请解答下列问题：（1）该企业员工中参加本次安全生产知识测试共有人；（2）补全条形统计图；（3）若该企业共有员工800人，试估计该企业员工中对安全生产知识的掌握能达到A级的人数．【解析】解：（1）20÷50%＝40，所以该企业员工中参加本次安全生产知识测试共有40人；故答案为40；（2）C等级的人数为40﹣8﹣20﹣4＝8（人），补全条形统计图为：（3）800×＝160，4. (2019 江苏省连云港市)为了解某地区中学生一周课外阅读时长的情况，随机抽取部分中学生进行调查，根据调查结果，将阅读时长分为四类：2小时以内，2～4小时（含2小时），4～6小时（含4小时），6小时及以上，并绘制了如图所示尚不完整的统计图．（1）本次调查共随机抽取了名中学生，其中课外阅读时长“2～4小时”的有人；（2）扇形统计图中，课外阅读时长“4～6小时”对应的圆心角度数为°；（3）若该地区共有20000名中学生，估计该地区中学生一周课外阅读时长不少于4小时的人数．【解析】（1）本次调查共随机抽取了：50÷25%＝200（名）中学生，其中课外阅读时长“2～4小时”的有：200×20%＝40（人），故答案为：200，40；（2）扇形统计图中，课外阅读时长“4～6小时”对应的圆心角度数为：360°×（1﹣﹣20%﹣25%）＝144°，故答案为：144；（3）20000×（1﹣﹣20%）＝13000（人），答：该地区中学生一周课外阅读时长不少于4小时的有13000人．【点评】本题考查条形统计图、扇形统计图、用样本估计总体，解答本题的关键是明确题意，利用数形结合的思想解答．5. (2019 江苏省泰州市) PM2.5是指空气中直径小于或等于2.5μm的颗粒物，它对人体健康和大气环境造成不良影响，下表是根据《全国城市空气质量报告》中的部分数据制作的统计表．根据统计表回答下列问题，2017年、2018年7～12月全国338个地级及以上市PM2.5平均浓度统计表（单位：μg/m3）（1）2018年7～12月PM2.5平均浓度的中位数为μg/m3；（2）“扇形统计图”和“折线统计图”中，更能直观地反映2018年7～12月PM2.5平均浓度变化过程和趋势的统计图是；（3）某同学观察统计表后说：“2018年7～12月与2017年同期相比，空气质量有所改善”，请你用一句话说明该同学得出这个结论的理由．【解析】（1）2018年7～12月PM2.5平均浓度的中位数为＝μg/m3；故答案为：；（2）可以直观地反映出数据变化的趋势的统计图是折线统计图，故答案为：折线统计图；（3）2018年7～12月与2017年同期相比PM2.5平均浓度下降了．点评本题考查了统计图的选择，利用统计图的特点选择是解题关键．6. (2019 江苏省无锡市)《国家学生体质健康标准》规定：体质测试成绩达到90.0分及以上的为优秀；达到80.0分至89.9分的为良好；达到60.0分至79.9分的为及格；59.9分及以下为不及格．某校为了了解九年级学生体质健康状况，从该校九年级学生中随机抽取了10%的学生进行体质测试，测试结果如下面的统计表和扇形统计图所示．各等级学生平均分统计表（1）扇形统计图中“不及格”所占的百分比是；（2）计算所抽取的学生的测试成绩的平均分；（3）若所抽取的学生中所有不及格等级学生的总分恰好等于某一个良好等级学生的分数，请估计该九年级学生中约有多少人达到优秀等级．【解析】（1）4%（2）92.1×52%+85.0×26%+69.2×18%+41.3×4%=84.1（3）设总人数为n个由题意得：80.0 ≤ 41.3×n×4%≤89.9所以48<n<54又因为4%n为整数所以n=50即优秀的学生有52%×50÷10%=260 人考向2统计图1. (2019 江苏省宿迁市)为了解学生的课外阅读情况，七（1）班针对“你最喜爱的课外阅读书目”进行调查（每名学生必须选一类且只能选一类阅读书目），并根据调查结果列出统计表，绘制成扇形统计图．男、女生所选类别人数统计表根据以上信息解决下列问题（1）m＝，n＝；（2）扇形统计图中“科学类”所对应扇形圆心角度数为°；（3）从选哲学类的学生中，随机选取两名学生参加学校团委组织的辩论赛，请用树状图或列表法求出所选取的两名学生都是男生的概率．【解析】解：（1）抽查的总学生数是：（12+8）÷40%＝50（人），m＝50×30%﹣5＝10，n＝50﹣20﹣15﹣11﹣2＝2；故答案为：20，2；（2）扇形统计图中“科学类”所对应扇形圆心角度数为360°×＝79.2°；故答案为：79.2；（3）列表得：由表格可知，共有12种可能出现的结果，并且它们都是等可能的，其中所选取的两名学生都是男生的有2种可能，∴所选取的两名学生都是男生的概率为＝．【点评】此题主要考查了列表法与树状图法，以及扇形统计图、统计表的应用，要熟练掌握．2. (2019 江苏省徐州市)某户居民2018年的电费支出情况（每2个月缴费1次）如图所示：根据以上信息，解答下列问题：（1）求扇形统计图中“910月”对应扇形的圆心角度数；（2）补全条形统计图．【解析】解：（1）补全表格如下：（2）由表知，共有12种等可能结果，其中积为9的有1种，积为偶数的有8种结果，所以积为9的概率为112；积为偶数的概率为82123=，故答案为：112，23．（3）从1~12这12个整数中，随机选取1个整数，该数不是（1）中所填数字的有5和7这2种，∴此事件的概率为21 126=，故答案为：16．点评此题考查的是用列表法或树状图法求概率．列表法可以不重复不遗漏的列出所有可能的结果，适合于两步完成的事件；树状图法适合两步或两步以上完成的事件．用到的知识点为：概率=所求情况数与总情况数之比．3. (2019 江苏省徐州市)某户居民2018年的电费支出情况（每2个月缴费1次）如图所示：根据以上信息，解答下列问题：（1）求扇形统计图中“910-月”对应扇形的圆心角度数； （2）补全条形统计图．【解析】解：（1）全年的总电费为：24010%2400÷=元 910-月份所占比：7280240060÷=， ∴扇形统计图中“910-月”对应扇形的圆心角度数为：73604260︒⨯=︒ 答：扇形统计图中“910-月”对应扇形的圆心角度数是42︒（2）78-月份的电费为：2400300240350280330900-----=元， 补全的统计图如图：点评考查条形统计图、扇形统计图的特点及反应数据的变化特征，两个统计图联系在一起，可以发现数据之间关系，求出在某个统计图中缺少的数据．4. (2019 江苏省盐城市)某公司共有400名销售人员，为了解该公司销售人员某季度商品销售情况，随机抽取部分销售人员该季度的销售数量，并把所得数据整理后绘制成如下统计图表进行分析．频数分布表请根据以上信息，解决下列问题：（1）频数分布表中，a＝、b＝；（2）补全频数分布直方图；（3）如果该季度销量不低于80件的销售人员将被评为“优秀员工”，试估计该季度被评为“优秀员工”的人数．【解析】解：（1）根据题意得：b＝3÷0.06＝50，a＝＝0.26；故答案为：0.26；50；（2）根据题意得：m＝50×0.46＝23，补全频数分布图，如图所示：（3）根据题意得：400×（0.46+0.08）＝216，则该季度被评为“优秀员工”的人数为216人．【点评】此题考查了频数分布直方图，用样本估计总体，以及频数分布图，弄清题中的数据是解本题的关键．5. (2019 江苏省扬州市)扬州市“五个一百工程“在各校普遍开展，为了了解某校学生每天课外阅读所用的时间情况，从该校学生中随机抽取了部分学生进行问卷调查，并将结果绘制成如图不完整的频数分布表和频数分布直方图．根据以上信息，回答下列问题：（1）表中a＝，b＝；（2）请补全频数分布直方图；（3）若该校有学生1200人，试估计该校学生每天课外阅读时间超过1小时的人数．【解析】解：（1）a＝36÷0.3＝120，b＝12÷120＝0.1，故答案为：120，0.1；（2）1＜t≤1.5的人数为120×0.4＝48，补全图形如下：（3）估计该校学生每天课外阅读时间超过1小时的人数为1200×（0.4+0.1）＝600（人）．【点评】本题主要考查频率分布直方图和频率分布表的知识和分析问题以及解决问题的能力，解题的关键是能够读懂统计图，并从中读出有关信息．6. (2019 江苏省镇江市)陈老师对他所教的九（1）、九（2）两个班级的学生进行了一次检测，批阅后对最后一道试题的得分情况进行了归类统计（各类别的得分如下表），并绘制了如图所示的每班各类别得分人数的条形统计图（不完整）．各类别的得分表已知两个班一共有50%的学生得到两个正确答案，解答完全正确，九（1）班学生这道试题的平均得分为3.78分．请解决如下问题：（1）九（2）班学生得分的中位数是；（2）九（1）班学生中这道试题作答情况属于B类和C类的人数各是多少？【解析】解：（1）由条形图可知九（2）班一共有学生：3+6+12+27＝48人，将48个数据按从小到大的顺序排列，第24、25个数据都在D类，所以中位数是6分．故答案为6分；（2）两个班一共有学生：（22+27）÷50%＝98（人），九（1）班有学生：98﹣48＝50（人）．设九（1）班学生中这道试题作答情况属于B类和C类的人数各是x人、y人．由题意，得，解得．答：九（1）班学生中这道试题作答情况属于B类和C类的人数各是6人、17人．【点评】本题考查的是统计图表与条形图的综合运用．读懂统计图表，从统计图表中得到必要的信息是解决问题的关键．条形统计图能清楚地表示出每个项目的数据．也考查了中位数与平均数．。