英文版大学物理功和能共44页
- 格式:ppt
- 大小:3.90 MB
- 文档页数:44










Time -averaged net forceWhen a time-varying net force isdifficult to measure, we can use a time-averaged net force as the substitute provided that it would give the same impulse to the particle in sametime interval.When a particle experiences a impact in a veryshort time, the non-impulse forces such as gravitational force and friction force are negligible compared to impulsive force.1f i t t F Fdtt =Δ∑∫J G J G ()F t ∑J G J p F t=Δ=Δ∑JG J G J GTime -averaged net force (continued)For a given amount of momentum change, we can delay the timeinterval to decrease the impulsive force.A baseball player catching a ball can soften the impact by pulling hishand back.Example:Example: Conical Pendulum.A small object of mass m is suspended from a string of length L . The object revolves in a horizontal circle of radium r with constant speed v . Determine the impulse exerted (1) by gravity, (2) by string tension on the object, during the time in which the object has passed half of the circle.Solution: From impulse-momentum theorem212122t net net t J F dt mv mv mv ==−=∫J G J G G G G The impulse exerted by gravity on the object 211222t mg t T r r J mgdt mg mgmg v v ππ====∫J G G G G GThe impulse exerted by string intension on the objectT net mgJ J J =−J G J G J G ()222222224T rmg r g J mv m v vvππ⎛⎞=+=+⎜⎟⎝⎠Impulse-momentum theorem for a system of particlesConsider a system of N interacting particles with masses m 1, m 2, …, m N .For i-th particle : the net external force the internal force exerted by j-th particle For the system of particles :According to Newton’s third law, the internal forces cancel in pairs.The total external force acting on the system:The total momentum of the system:i F J G ijf J G ()i ij iF f dt d p +=JG J G J G()i ij iij iiF f dt d p ≠+=∑∑∑JG J G J Gij ij if ≠=∑∑J G iiF ∑J Gtotiip p =∑JG J G §2Impulse -momentum theorem fora system of particlesImpulse-momentum theorem for a system of particles (continued)zerototd p J GWhich case of collision satisfies the conservation of momentum? Or conservation of component momentum?Example②Example: A wooden block of mass M 1is suspended from a cord of length L attached to a cart of mass M 2which can roll freely on a frictionless horizontal track. A bullet of mass m is fired into the block from left. After the impact of the bullet, the block swings up with the maximum angle of θ. What is the initial speed v of the bullet?Solution:(1)Stage 1:For the systemconsisting of m and M 1, the momentum isconserved in horizontal during a small intervaltime of impact.11()mv M m v =+Example: is suspended vertically with its lowest end§3 Center of MassDescribe the motion of a system of particlesby every motion for individual particles by overall motion in terms of center of mass Center of massFor the system of discretely distributed particles represented by components For the extended object with uniformly distribution of mass CM i i i i i i i i m r m r r m M==∑∑∑G G G CM CM CM i i i i i i ii i m x m y m z x y z M M M ===∑∑∑10CM 10CM lim 1, lim 11, i i N i i N i m N i N i m CM x m x dm x x dm M dm m y y dm z z dm M M →∞=Δ→→∞=Δ→Δ===Δ==∑∫∫∫∑∫∫CM 1r r dm M=∫GGExample: Find the center of mass of a uniform solidhemisphere of radius R and mass M .Solution: From symmetry it is apparent that the center ofmass lies on the z axis. x CM =0, y CM =0.The three-dimensional integral can be treated as an one-dimensional integral. Subdivide the hemisphere into a pile of thin disk .CM 11z zdm z dV M Mρ==∫∫2dV r dzπ=323M R ρπ⎛⎞=⎜⎟⎝⎠022CM 323322003cos sin (sin )233cos sin sin (sin )22313248z R R R d R R d R d R R πππθθθθθθθθθ=−===×=∫∫∫Find r , z in terms of θ.sin cos sin r R z R dz R d θθθθ===−Supplement problem: Find the center of mass of a uniform semicircular plate of radius R and mass M.Applications of center of massFor a system of discrete particlesA cannon shell in a parabolictrajectory explodes in flight,splitting into two fragments. Thefragments follow new paths, butcenter of mass continues on the original parabolic trajectory.For a rigid bodyWe can describe a rigid body as a combination of translational motion of the center of mass and rotational motion about an axis throughthe center of mass.Fig. (a) The motion of the diver is pure translation.Fig. (b) The motion of the diver is translation plus rotation.Example: A rocket is fired into the air. At the moment it reaches its highest point,a horizontal distance d from its starting point, an explosion separates it intotwo parts of equal mass. Part I is stopped in midair by explosion and fallsvertically to Earth. Where does par II land?Solution: After the rocket is fired, the path of the center of mass of the system continues to follow the parabolic trajectory of a projectile acted on only by a constant gravitational force. The center of mass will thus arrive at a point 2d from the starting point. Since the masses of I and II are equal,the center of mass must be midway between them. Therefore, II lands a distance3d from the starting point.Example:Solution II: Treat the two blocks as a whole.External force: exerted by wall on m 2.2CM2122()()d x k l x m m dt −=+2CM 212m x x m m =+2CM12CM 1222()()d x m m k l x m m m dt+−=+2CM 2CM 22120d x m k x l dt m m m ⎛⎞+−=⎜⎟+⎝⎠2CM 122cos m k x l A t m m m φ⎛⎞−=+⎜⎟⎜⎟+⎝⎠。
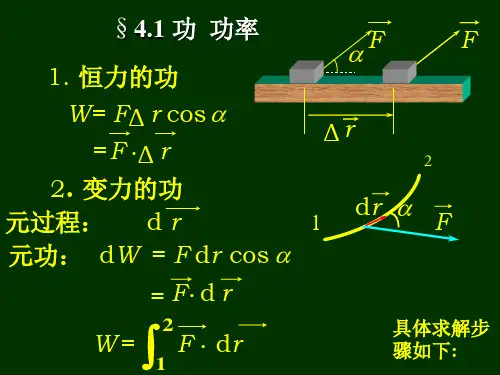
Chapter 4 Work and EnergyThe concept of energy is one of the most important in the world of science. In everyday usage, the term energy has to do with the cost of fuel for transportation and heating, electricity for lights and appliances, and the foods we consume. However, these ideas do not really define energy. They tell us only that fuels are needed to do a job and that those fuels provide us with something we call energy.Energy is present in the Universe in a variety of forms, including mechanical energy, chemical energy, electromagnetic energy, heat energy, and nuclear energy. Although energy can be transformed from one form to another, the total amount of energy in the Universe remains the same. If an isolated system loses energy in some form, then by the principle of conservation of energy, the system must gain an equal amount of energy in other form. The transformation of energy from one form into another is an essential part of the study of physics, chemistry, biology, geology, and astronomy.In this chapter we are concerned only with mechanical energy. We introduce the concept of kinetic energy, which is defined as the energy associated with motion, and the concept of potential energy, the energy associated with position. We shall see that the ideas of work and energy can be used in place ofNewton’s law to solve certain problems.4.1 Work and Power1. Work W done by a constant force is defined as the product of the component of the force along the direction of displacement and the magnitude of the displacement.ϕcos FS S F W =⋅=Where the force makes an angle of ϕ with displacement .SThe SI unit of work is the joule (J), named for James Prescott Joule, an English scientist of the 1800s. It is derived directly from the units for mass and velocity:1joule=1J=1(kg) (m/s 2) (m)=1 kg m 2/s 22. Work done by a variable force(1). The increment of work dW done on the particle by F during the displacement d r isr d F dW ⋅=, where Force F is function of its position.(2). The work W done by F while the particle moves from an initial position a to a final position b is then⎰⎰⋅==b a b a r d F dW W(3). We use the components ofF and r d to express the forceand displacement, then we havedzF dy F dx F k dz j dy i dx k F j F i F r d F W z y b a x z y b a x b a ++=++⋅++=⋅=⎰⎰⎰)()( 3. Work done by multiple forces : If there are several forces act on a particle, we can replace F in above equation with the net force ∑F , where +++=∑321F F F F , where j F are theindividual forces. Then+++=⋅+++=⋅=⎰⎰321321)(W W W r d F F F r d F W b aba 4. Power(1). The rate at which work is done by a force is said to be the power due to the force . If an amount of work W is done in a time intervalt ∆ by a force, then the average power due to the force is t WP ∆=.(2). The instantaneous power P is the instantaneous rate of doing work, which can be written asv F dtr d F dt dW P ⋅=⋅==. (3). The SI unit of power is the joule per second . This unit is used so often that it has a special name, the watt (W), after James Watt, who greatly improved the rate at which steam engines could do work.4.2 Kinetic Energy and Work-Kinetic Energy TheoremEnergy is a scalar quantity that is associated with a state of oneor more object. The term state here has its common meaning: it is the condition of an object.1. Kinetic energy K is associated with the state of motion of an object. The faster the object moves, the greater is its kinetic energy. For an object of mass m and whose speed v is well below the speed of light , we define kinetic energy as 221mv K = The SI unit of kinetic energy is the same as work —joule.A convenient unit of energy for dealing with atoms or with subatomic particles is the electron-volt (eV).1 electron-volt = 1 eV =1.60 x 10 –19 J.2. Work-kinetic energy theorem : If a force changes the speed of an object, it also changes the kinetic energy of the object. If the kinetic energy is the only type of energy of the object being changed by the force, then the change in kinetic energy is equal to the work W done by the force:W K K K i f =-=∆ Here i K is the initial kinetic energy (=2021mv ) and f K is the kinetic energy (221mv ) after the work is done.3. We can prove work-kinetic energy theorem as follow:002022222221212121)(21k f v v b a z y x z z y y x x b a b a b a K K mv mv v m mvdv W dv v v v d dv v dv v dv v v d v v d v m dt v dtv d m s d f W -=-====++=++=⋅⋅=⋅⋅=⋅=⎰⎰⎰⎰(Numerator and denominator of a fraction)4.3 Work done by weight and by a spring force1. Work done by weight :[]a b a b b a b a m gh m gh h h m g dh m g dW W m gdhm gdl m gdl l d g m dW --=--=-==-=--==⋅=⎰⎰)()cos(cos απαWe can find that the work done by weight on a particle between two points does not depend on the path taken by the particle . Or no matter what path we choose to move the particle, the work done by its weight is the same . In other word if we move a particle around a closed path, the work done by weight on the particle is zero .2. Work done on aparticle-like object by aparticular type of variableforce, namely, springforce —the force exertedby a spring.⎥⎦⎤⎢⎣⎡--=-=-==-=⋅=-=⎰⎰222212121'a b x x x x b a kx kx x k kxdx dW W kxdxs d F dW law s Hook kx F b a b a 3. Conservative force and Non-conservative force : If the workdone by the force is independent of the path the particle moves,the force is a conservative force ; otherwise a non-conservative force . Weight and spring-force are conservative forces; friction is a non-conservative force.4.4 Potential energyPotential energy U is energy that can be associated with the configuration (or arrangement) of a system of objects that exert a force on one another. If the configuration of the system changes, then the potential energy of the system also changes.1. We know that work done by a conservative force has nothing to do with the path the particle taken. So we can introduce a quantity which is the function of the state of the system to indicate this kind of nature for a conservative force. We call it potential .2. Gravitational Potential Energy(1). The work done by weight can be expressed as: []U mgh mgh W a b ∆-=--==, where U ∆ is the change in the gravitational potential energy. Since the work done by weight has definite magnitude from an initial position to a final position, so only a changeU ∆ in gravitational potential energy is physically important .(2). However, to simplify a calculation or a discussion, we cansay that a certain gravitational potential U is associated with any given configuration of the system, with the particle at a given height h. To do so, we rewrite the above equation as:)(i i h h mg U U -=-Then we take i U to be the gravitational potential energy of thesystem when it is in a reference configuration, with the particle at a reference pointi h . Usually, we set 0=i U and 0=i h , then we have mgh U =. So the gravitational potential energy associated with a particle-Earth system depends on the height h of the particle relative to the reference position of h i =0, not the horizontal position.3. Elastic Potential Energy(1). Similar to a particle-Earth system, the work done by the spring force can be rewritten as U kx kx W a b ∆-=⎥⎦⎤⎢⎣⎡--=)21()21(22.(2). To associated a potential energy U with any given configuration of the system, with the block at position x, we set the reference point for the block as x i =0, which is always at the equilibrium position of the block. And we set the corresponding elastic potential energy of the system as U i =0. Thus we have 221)(kx x U =. Attention: (1). Potential energy belongs to the whole system.(2). The magnitude of potential energy depends onthe choice of the reference point.4.5 Work-Energy Theorem and Conservation of Mechanical Energy1. Work-kinetic energy theorem for one particle: We have W K K K i f =-=∆2. Work-Energy Theorem: Suppose we have particles of N in the system we discussed and we use work-kinetic energy theorem for each particle, then we have total amount of N equations like those:jijf j if if K K W K K W K K W -=-=-=222111We can divide the forces exerted on every particle into external forces and internal forces. And the internal forces can also be classified as conservative internal forces and non-conservative forces. Summing the two side of above equations, we will have: i fN j ji jf N j j K K K K W -=-=∑∑==11)(Or to be exactly,K W W W noncon in con in ext ∆=++--We also know that the work done by the conservative internalforce can be written as the minus difference of potential energy. So we get the Work-Energy Theorem :E U K W K W W con in noncon in ext ∆=∆+∆=-∆=+--The work done by external forces and non-conservative internal forces in a given system is exactly equal to the difference of its Mechanical Energy .3. Conservation of Mechanical Energy : When only conservative forces act within a system, the kinetic energy and potential energy can change. However, their sum, the mechanical energy E of the system, does not change . 0=∆+∆=∆U K E4.6 Reading a Potential energy curveConsider a particle that is part of a system in which a conservative force acts. Suppose that the particle is constrained to move along an x axis while the conservative force does work on it.1. Finding the Force Analytically : For one-dimensional motion, the work W done by a conservative force that acts on a particle as the particle moves, and the potential energy have the relation as followdx x F dW x U )()(-=-=∆So can get the force from the potential energytion ensionalmo one dx x dU x F dim )()(--=We can, for example, check this result by putting221)(kx x U =, which is the elastic potentialenergy function for a springforce. Above equation yieldskx x F -=)( as expected.2. The Potential EnergyCurve : The following figureis a plot of a potential energyfunction U(x) for a system inwhich a particle is inone-dimensional motionwhile a conservative forceF(x) does work on it. We caneasily find F(x) by taking theslope of the U(x) curve atvarious points. Fig. (b) is a plot of F(x) found in this way.3. Tuning Point : Since there is only conservative force acting on the particle, the system will remain conservation of its mechanical energy. So we have)()(x U E x K -=. Since kinetic energy)(x K is not less than zero. As the particle moves from 2xto 1x (Fig. a), when the particle reaches 1x , its kineticenergy is zero, meanwhile the force on the particle is positive. It means the particle does not remain atx but instead begins to1move back to the right. Hencex is a tuning point, a place1where K=0 and the particle changes direction of its motion.4.Equilibrium Points:Neutral equilibriumUnstable equilibriumStable equilibrium。