当前位置：文档之家 › 大学物理功和能

大学物理功和能

  • 格式：docx
  • 大小：78.79 KB
  • 文档页数：3

下载文档原格式

  / 3

合集下载

大学物理第四章--功和能

大学物理第四章--功和能
a
a
l
xdx
2l
前已得出：
Af
mg(l a)2
2l
mg(l 2 a2 ) mg(l a)2 1 mv2
2l
2l
2
得v
g l
1
(l 2 a 2 ) (l a)2 2
§3 保守力的功与势能 一、 保守力
rB
B
两个质点之间的引力
B
第四章 功和能
§4.1 功 §4.2 动能定理 §4.3 保守力功与势能 §4.4 功能原理机械能守恒定律
§1 功和功率
一、恒力做功 直线运动
A=Fcos S
记作A F S F r
F
F

M
M
S
位移无限小时：
dA

F

dr
dA称为元功
功等于质点受的力和它的位移的点积(标积)
例１一水平放置的弹簧，其一端固定，另一端系一小球，求小
球的位置由A到B的过程中弹力对它所做的功。（在O处弹簧无 形变）
解：根据胡克定律 F F kx
W F dr

xB Fdx
xA
xB xA

kxdx

O

1 2
A
k xB2
B
xA2

1 2
k xA2
作用在质点
上．在该质点从坐标原点运动到(0，2R)位
置过程中，力
F
对它所作的功为多少？
y
b
b
A a F.dr a (Fxdx Fydy)
R
x O
例4 如图，水平桌面上有质点 m ，桌面的摩 擦系数为μ 求：两种情况下摩擦力作的功

大学物理第04章_功和能

大学物理第04章_功和能

Ek
1 2
mv2
单位：（J）
设质点m在力的作用下沿 曲线从a点移动到b点
dr
b
元功：
F
dW F dr F cosds a
F cos
ma
m dv dt
dW
F
cosds m
dv ds dt
mvdv
总功：
W
dW
v2 v1
mvdv
1 2
m(v22
v12 )
质点的动能定理：
合外力对质点所做的功等于质点动能的增量。
对系统内所有质点求和
i
n
n
n
n
Wi内 Wi外 Ek2i Ek1i
fi
i 1
i 1
i 1
i 1
W内 W外 Ek 2 Ek1
质点系的动能定理：
质点系动能的增量等于作用于系统的所有外力和 内力作功之代数和。
值得注意：
内力做功可以改变系统 的总动能。
例3 如图所示，用质量为M的铁锤把质量为m 的钉子 敲入木板。设木板对钉子的阻力与钉子进入木板的深 度成正比。在铁锤敲打第一次时，能够把钉子敲入 1cm深，若铁锤第二次敲钉子的速度情况与第一次完 全相同，问第二次能把钉子敲入多深？
dxi dyj dzk
bx ax
Fxdx
by ay
Fydy
bz az
Fzdz
在自然坐标系中
F F e Fnen dr dse
W
b
F dr
a
b
a F e
Fnen
dse
s1 s0
F
ds
附:功率的定义：
功率是反映作功快慢程度的物理量。
功率： 单位时间内所作的功。

大学物理-力学中的功和能1

大学物理-力学中的功和能1
W重力 = mgR
dh
drv
ϕ
mg
水平方向无外力，水平方向系统 动量守恒。
mv + MV = 0
V = − mv M
W重力
+ W内力
=
1 2
MV
2
+
1 2
mv
2
V = − mv M
对M，内力 N ’ 所做的功， 由质点的动能定理可得：
WN′
=
1 2
MV
2
=
m2v 2 2M
mN
M N’
对m，内力 N 所做的功
x1
y24dy
y1
∫ ∫ =
3 −2
x2 2
dx
+
9 4 4dy
1
4y = x+6
y
2.25
a 1
−2 O
＝ 10.8 J
x2 = 4y
b
3x
若质点沿直线运动
∫ ∫ ∫ W2 =
b a
(Fxdx
+
Fydy)
=
2 x2 ydx +
x1
y24dy
y1
∫ ∫ =
3 −2
1 2
(
x
+
6)d
x
+
9 4 4dy
Q2
？
例：有一面为 1/4 凹圆柱面（半径 R，质量 M），放置在 光滑水 平面上。一小球（质量 m），从静止开始沿圆柱面从顶端无摩擦 下落（如图），最终从水平方向以速度 v 飞离物体 ，求：1）此 过程中重力所做的功；2）内力所做的功。
m M
解：重力只对小球做功
R dW重力 = mg drv cosϕ = mgdh

大学物理ch3 功和能

大学物理ch3 功和能

= mg tanθ cosθ ds
= mgL tan θ cos θdθ
0 θ0
= mgL(1 − cos θ0 )
2
2016/3/3
书中例题3.2 (p.98)（重点） 一条长L，质量M的均匀柔绳，A端挂在天花板上，自然下垂，将 B端沿铅直方向提高到与A端同高处。 求：该过程中重力所作的功。 解：提升高度y时，提的链长y/2 提起部分的质量
力与位移的夹角在变的例子
求 θ = θ0 时，F 作的功。
解
例 已知用力 F 缓慢拉质量为m 的小球，F 保持方向不变


3.2 几种常见力的功
一.重力的功
重力mg 在曲线路径 M1M2 上的功为
z
Z2
M1
②
F − T sin θ = 0
T cosθ − mg = 0
F = mg tanθ A = F ⋅ dr = F cosθ ds
m1
Ai = Ai外 + Ai内
i i i
讨论 (1) 内力和为零,内力功的和 是否为零？ 不一定为零
v m2 2 v4 m3 v3
f1
B A S
v1 m4
∵功是标量，其和为代数和。 内力总是成对出现的，按照牛顿第三定律，这一对力 的矢量和为0，但这一对力所作的功的和不一定为0。
f2
b0 =
μ0 l 1 + μ0
1 1 1 ρg (l 2 − b 2 ) − μρg (l − b) 2 = ρlv 2 − 0 2 2 2
v=
当 y >b0 ，拉力大于最大静摩擦力时，链条将开始滑动。
g 2 2 μg (l − b ) − (l − b) 2 l l

大学物理课件第4章-功和能

大学物理课件第4章-功和能

如图,求船从离岸 x1处移到 x2 处的 过程中,力 F 对船所作的功.
F
解:判别F 是否为变力作功(大小不变,方
向变元),功属于dW变力作F功.建dx立坐F标,取dx元过co程sa
h
o x2
a
dx x x1 x
cosa x
x2 h2 x
dW F dx
x2 h2
功在数值上等于示功图
F
曲线下的面积。
3. 功率
0 x1
x2 x
dx
平均功率: P =ΔΔWt
瞬时功率:
P
= lim
Δt 0
Δ Δ
Wt =
dW dt
=
F
. dr
dt
= F .v
[ 例1 ] 有一单摆，用一水平力作用于m
使其极其缓慢上升。当θ 由 0 增大到 0 时，
求: 此力的功。
{
F T sinθ T cosθ mg
两边平方
v 2 v12
由动量守恒
2v1

v2

v 22
v
v1
v2
由机械能守 恒（ 势能无变化）
v2

v12

v
2 2
v1 v2 0 两球速度总互相垂直
例8：已知半圆柱形光滑木凹槽，放在光滑桌面上，
如图，求质点下滑至最低点时给木块的压力.
解：
mv MV 0
•2.碰撞分类
正碰 斜碰
（从碰撞前后两球中心连线角度分类 ）
弹性碰撞 非弹性碰撞 完全非弹性碰撞
一般非弹性碰撞
（从碰撞能量损失角度分类）
例7：在平面上两相同的球做完全弹性碰撞，其中一球开始时处于

大学物理之功、能、能量守恒定律

大学物理之功、能、能量守恒定律

大学物理之功、能、能量守恒定律
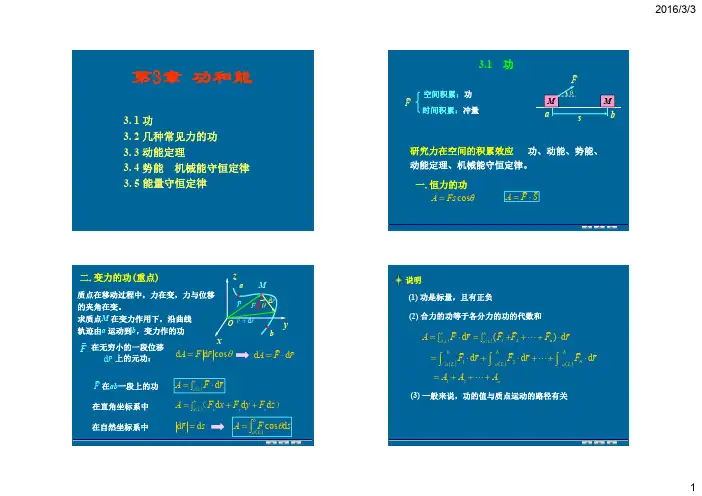
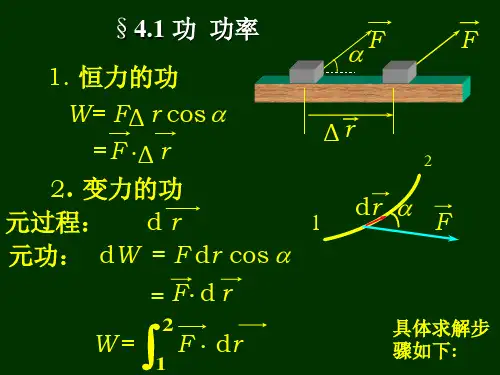
功
1、恒力做功（矢量的标积）。

2、变力做功（微分形式、矢量的标积）。

3、功率。

动能
1、公式及动能定理。

2、刚体的动能及其动能定理（转动的问题）。

势能
1、重力势能公式、重力的功等于重力势能增量的负值。

2、弹性势能公式、弹性力的功等于弹性势能增量的负值。

3、引力势能公式、万有引力的功等于引力势能增量的负值。

保守力和非保守力
保守力做功只与物体的始末位置有关和路径无关。

保守力做正功，系统的势能减少。

保守力做负功，系统的势能增加。

物体沿闭合路径绕行一周，保守力的功等于零。

非保守力如摩擦力，做功与路径有关。

能量守恒定律（机械能、非机械能）（保守力、非保守力）
1、一孤立系统的各种形式的能量保持不变，成为能俩功能守恒。

2、孤立系统中，机械能增加或减少时就有等量的非机械能减少或增加，从而保持机械能和非机械能之和不变。

3、孤立系统内只有保守力做功时，机械能保持不变。

4、外力和系统内非保守力所做功的总和，等于系统机械能的增量，称为系统的功能原理。

多做题，多分析，多复习。

大学物理功和能课件讲义

大学物理功和能课件讲义

解: 以雪橇、冰道和地球为一系统，由功能原理得
Af E2 E1
E2 E1 mgh
Af mg cos s' mgs mg(s's)
mg(s's) mgh
代入已知数据有 s h s' 500m
例4.5 一半径为 R的四分之一圆弧垂直固定于地面上，
止，距离为a. 在万有引力作用下,
两者距离变为b. 在此过程中,万有引
力做的功A=.
解： A Epa Epb
( Gm2 ) ( Gm2 )
a
b
Gm2 (a b)
ab
[思考]两者距离为b时的速率？
[例4-8] 质量为m的质点在指向圆心的力
F=k/r2 的作用下，作半径为r的
圆周运动，若取Ep=0，则系统的机
2. 力学中常见的势能函数
(1) 万有引力势能
由
Aab
(
Gm1m2 ra
) (
Gm1m2 rb
)
=
EPa－EPb
以r→∞时为万有引力势能零点，即令 EPy 0
由任一状态势能值的定义,可得 两物体相距r时的万有引力势能
EP引
EP引
Gm1m2 dr Gm1m2
r
r2
r
O
r
E
P引
G m1m 2 r
一、保守力的定义
1.万有引力的功 —与路径无关 rb
dr
dA以MF处G Md为rm原点rG，Mr2m
r0
dr
r2
dr r
M
r
ra m
(r0
r） r
GMm
r 2 dr
rb
A
rb
ra

大学物理-力学中的功和能1

大学物理-力学中的功和能1
1.5 功和能（Work and Energy)
§1 功 Work
一、功的概念
功的两要素
力 在力的方向上的位移
二、恒力的功
v
W W
= F ∆rv cosθ
= Fv ⋅ ∆rv
=
Fr
∆rv
讨论： 功是标量，但有正负
Fn
F
θ
∆rv
Fr
0≤θ
<
π 2
,W
>0
π 2
<
θ
≤
π,
W
<0
θ
=
π 2
,W
=0
三、变力的功
元功
dW
=
v F
⋅ drv
b
质点从 a → b 的功 A
W=
b
∫
Fv
⋅
drv
=
b
∫
F
drv
cosθ
b
= ∫ F cosθ ds
a( L)
a( L)
a( L)
drv θ
v F
a (L)
直角坐标系中
v F
=
v Fxi
+
F
y
v j
+
v Fz k
drv = dxiv + dyvj + dzkv
∫ ( ) ∫ W =
Fydy)
=
2 x2 ydx +
x1
y24dy
y1
∫ ∫ =
3 −2
1 2
(
x
+
6)d
x
+
9 4 4dy
1
＝ 21.25 J

大学物理3 功与能

大学物理3 功与能

3，功率
A2 F2 dr ......
(1)
下一张
返回
例1，如图所示，劲度系数为k ，原长为AB 的弹 簧，一端固定于A 点，另一端连接一个质量为m、 靠在半径为R 的光滑圆柱面上的物体。在变力F 的 作用下,物体缓慢地沿表面从B移到C (BOC= ), 求变力所做的功。 F m 解：分析受力如图所示。 d C T 弹簧弹性力 T kx kR R O mg B F mg cos kR 变力F 为：
A x
EKB
（2）根据动能定理,合力所做的功等于质点动能的增加。
1 A EkB EkA m 2 (a 2 b 2 ) 2 上一张
下一张
返回
计算分力功： r a cos t i b sint j x i y j 2 2 a a cos t i b sint j 2 2 2 r xi yj
内力：系统内部各物体之间的相互作用。
外力：系统外对系统内物体施加的力。
上一张
下一张
返回
动能定理小结：
A Ek 2 Ek 1
1 2 E 对于单个质点， A F dr ， F 为合力， k mv
2
对于质点系，A 为所有力的功， A
A外 A内 1 1 2 2 Ek 为总动能 Ek m1v1 m2v2 ...... 2 2

y
N F 100 300 f G
x l
由此可得摩擦力
f N 145 N
A4＝f l cos 435 J
因为重力和摩擦力在这里是阻碍物体运动的力， 所以它们对物体所作的功都是负值。
上一张 下一张 返回

大学物理 功和能汇总

大学物理 功和能汇总
0 1
2 动能定理： A 1 2 mv 0
2A v 4 m s m
[思考] 在 x =0 至 x =1m 过程中， F 的冲量？
10
§4.3 质点系的动能定理
Theorem of Kinetic Energy for a system of Particle
对第 i 质点 求和
O 张力不做功，重力做功： 用动能变化定理解：

l
m
T

A mg dl mg dl cos
mgl cos d mgl sin 0 1 2 mgl sin mv 2


ˆn e

v
mg
ˆt e
比直接解牛顿方程简单，但仍作积分运算。
13
§4.4 *柯尼希定理
i
14
一对力 的功
内力总是成对出现 dr1 两质点间的内力 f ij 和 f ji ,
B1
B2
dr2
f 12
称为一对力 f ij f ji
m1
r21
f 21
m2
A1
A2
一对力做的功之和
dA = f12 dr1 + f21 dr2
f 21 dr2 dr1 f 21 dr21
mi ac dri
m i ac
z
y
mi
= ac mi dri
ri
ac
C 质心 O
12
= ac d mi ri = 0 A i
B
x
=
0
【例】柔软细绳长为l，小球质量为m，求摆下至 角时小球的速度和绳的张力。

大学物理第4章 功和能

大学物理第4章 功和能

f d r 0 （此式也可作为
L
(1 ) ( 1 ) f d r ( 2 ) f d r L1 L2
(2)
L1
L2
保守力的定义） 20
二. 几种保守力 1.万有引力
(2) ×
d r er d r
W 12 对 ( 1 )
(2)
13
本质区别：动能和物体的运动状态相联系，任 一运动状态对应一定的动能，是状态量；而功 是与物体在力作用下的具体运动过程相联系， 它一般是路径的函数，因而功是过程量。 密切关系：过程便意味着状态变化。合外力对 质点做功，质点的动能便发生变化。做功是使 质点动能改变的手段，动能的变化又是用功来 量度的，故二者具有相同的单位。 动能是质 点因运动而具有的做功本领。
——质点的动能定理
“合外力对质点所做的功等于质点动能的增量”
12
2. 分析说明： ①动能定理本质上是牛顿第二定律的推论，它 从一个侧面反映了质点在力学过程（空间积累 过程）中所服从的规律。 ②由动能定理知，力对物体做功，能改变物体 的动能，也只有力对物体做功，物体的动能才 能改变， 功是机械运动能量变化的量度。 ③功和动能的概念不可混淆
14
3. 质点系的动能定理 质点：m1 、 m2
F F 内力： f 1 、f 2 外力： 1 、 2 初速度： 1 a 、 2 a 末速度： 1b 、 2 b
b
v1b
dr b · b·
1 2
v2b
F2
2 2
F1
dr1 m1
m ·
f1 f2
·
m1:
m2:
2 2 2 ( F 1 f 1 ) d r1 1 m 1 1 b 1 m 1 1 a ( 1 ) a 1 2 2 b 2 2 2 ( F 2 f 2 ) d r2 1 m 2 2 b 1 m 2 2 a ( 2 ) a 2 2 2

大学物理力学第四章功与能

大学物理力学第四章功与能
（1）一对力的功与相对移动的路径无关，而只决 定于相互作用物体的始末相对位置，这样的一对 力称为保守力 （如：万有引力、弹力、重力）
（2）保守力B的环流 为零A。
y
A
F dr l1
F
A B
dr
l2
B
B
F dr
l1
l1
A F dr l2
F dr
A
l2
B
0
o
x
非保守力——▲ 摩擦力（耗散力):作功为负，
1 2
m2v2 B 2
1 2
m2v2
2 A
B1
B2
B1
B2
F1 • d r1 F 2 • d r2 f 1 • d r1 f 2 • d r2
A1
A2
A1
A2
1 2
m1v1B 2
1 2
m2v2B 2
1 2
m1v1A2
1 2
m2v2 A2
Aext Aint EkB EkA
外力与内力对质点系做的功之和等于质 点系总动能的增量。-----质点系的动能定理
A
rAB
B
A F r cos
F r
恒力的功与物体的具体路径无关，
只和起点和终点位置有关.
2. 变力做功
A
F1
r1
F2
r2
F3
r3
...
Fi
ri
...
ri i
定义: element work元功
Fi
dA F dr 视为恒力,直线
r3
F3
r2 r1
F2
F1
A
B
AAB L
E。
n
n

大学物理功和能

大学物理功和能
解：只有保守力（重力)做功， 机械能守恒.（以桌面为零势能点）
0
E2 E1
l
0
m L
l
g
l 2
1 mv 2 2
m L
x
g
x 2
0
v g ( x2 l2 ) L
x
例3 ： 一轻弹簧, 其一端系 在铅直放置的圆环的顶点P， 另一端系一质量为m 的小球, 小球穿过圆环并在环上运动
(μ=0)．开始球静止于点 A,
Wab (EPb EPa ) 势能定理
末位置的函数
始位置的函数
引力的功
W
(G
m' m )
rB
(G
m'm
rA
)
弹力的功
W
(
1 2
kxb
2
1 2
kxa
2
)
引力势能
Ep
G
m' m r
弹性势能
Ep
1 2
kx2
重力的功
重力势能
W ( mgzb mgza )
W mgz(mgh)
势能定理
Wab (EPb EPa )
力分为内力和外力，内力又分为保守和非保守力
1. 保守力 某些力对质点做功的大小只与质点的始末位置有关， 而与路径无关。这种力称为保守力。 典型的保守力： 重力、万有引力、弹性力
静电力 与保守力相对应的是耗散力
典型的耗散力： 摩擦力
a.重力的功
m在重力作用下由a运动到b，取地面为坐标原点.
WG
瞬时功率：P lim W dW
t0 t
dt
例1.作用在质点上的力为 F 2 yi 4 j( N ) 分别计算 质点沿着抛物线 x2 4 y 和 4 y x 6 的直线从

大学物理功与能

大学物理功与能

赵
承 均
W F rr cos
r
F
用矢量点积或标积表示：
rr
W
r F
rr
单位：焦耳( J )，N ·m
第一篇 力学
注意
重 ①.功是标量，只有大小正负之分。
大 数 理
(0, ), cos 0,W 0
学
2
院
,cos 0,W 0
赵
2
承
均
( , ), cos 0,W 0
2
力对物体做正功； 力对物体不作功； 力对物体做负功。
理
学 院
x
W k xdx xo
赵 承 均
1 k x2 2
x xo
1 2
kxo2
1 2
kx2
0
r F
x r x dx xo
即：此情形弹力做正功。
第一篇 力学
二、功率
力的功率描写该力对质点做功快慢的物理量，即单位时间内该力对质
重 点所做的功。
大
数 理
1.平均功率
mean power
学 院
外力作功与时间之比： P W
任何一对相互作用力做功的代数和仅决定于两物体的相对位移，而
与参考系的选择无关。
[D]
第一篇 力学
⑤.功是力与位移的点积，而位移依赖坐标系的选择，所以功与参照系有关。
重
大 数 理
例如：传送带将箱子从低处运到高处，地面上的人看摩擦力对箱子作正 功，而站在传送带上的人看摩擦力没有作功。
学
院
赵 承 均
第一篇 力学
②.多个力对物体作功，等于各力对物体作功的代数和。
证明： W
r F
rr
rr (F1 F2 L

大学物理1.5-功与能-PPT文档资料

大学物理1.5-功与能-PPT文档资料
h1 h1
h2
h2
四. 合力的功
AAB A F dr F1 F2 ... FN dr B B B A F1 dr A F2 dr ... A F dr
B
A1 AB A2 AB ... ANAB
ri
mg i
解： dA F dr mg d r cos d r cos dh
b h2
h1
dA m gdh
A dA mgdh
b a
h2 h1
mg h1 h2
与弹性力一样，重力所作的功只取决于运动物体的 起﹑末位置，与中间过程无关。
0
由此式可见，弹力的功只与小球的初末位置有关，而 与移动的中间过程无关，例如若先将 m 从 x1 点向右拉 伸，然后再压缩至x2点，弹力的功仍为上式。
三﹑质点沿曲线运动时变力的功
元功
B
Ai Fi ri
Ai Fi ri cos i
AAB lim
r 0 i
解： F mg y ˆ ˆ dyy ˆ d r dxx
A F dr
r1 r2
h
a
ri
mg i b h2
h1
ˆ (dxx ˆ dyy ˆ) mg y
r1
r2
ˆ dyy ˆ mg dy mg ( h1 h2) mg y
F（xi） i
x x1 x1 ... x i ... x n
Ai F ( x i )x i cos i f x ( x i )x i
x1
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

第四章 功和能
P88-92习题：3、4、5、12、13、14、19、23、27、30、36、
一. 选择题：
3．如图4-18所示，一质点在如图所示的坐标平面内作圆周运动，有一力
0()+F =F i j x y 作用在质点上．在该质点从坐标原点运动到(0，2R ）位置过程中，力F 对它所作的功为（ ）。

(A) 20R F ． (B) 2
02R F ．
(C) 2
03R F ． (D) 2
04R F ．
［ ］
4．如图4-19所示，，木块m 沿固定的光滑斜面下滑，当下降h 高度时，重力作功的瞬时功率是（ ）。

(A)2
1)
2(gh mg ． (B)2
1)
2(cos gh mg θ．
(C)1()21/2
mgsin θgh (D) (2)1/2mgsin θgh
［ ］
5．质量为m ＝0.5 kg 的质点，在Oxy 坐标平面内运动，其运动方程为x ＝5t ，y =0.5t 2（SI ），从t =2 s 到t =4 s 这段时间内，外力对质点作的功为（ ）。

(A) 1.5 J ． (B) 3 J ．
(C) 4.5 J ．
(D) -1.5 J ．
［ ］
二. 填空题：
12 ．已知地球质量为M ，半径为R ．一质量为m 的火箭从地面上升到距地面高度为2R 处．在此过程中，地球引力对火箭作的功为_____________________．
13．某质点在力F ＝(4＋5x )i (SI)的作用下沿x 轴作直线运动，在从x ＝0移动到x ＝10 m 的过程中，力F 所做的功为__________．
图4－18 习题4-3图 图4－19 习题4-4图
14．二质点的质量各为m 1，m 2．当它们之间的距离由a 缩短到b 时，它们之间万有引力所做的功为_ __．
19．如图4-24所示，劲度系数为k 的弹簧，一端固定在墙壁上，另一端连一质量
为m 的物体，物体在坐标原点O 时弹簧长度为原长．物体与桌面间的摩擦系数为μ．若物体在不变的外力F 作用下向右移动，则物体到达最远位置时系统的弹性势能E P ＝_____．
23．如图4-27所示，劲度系数为k 的弹簧，上端固定，下端悬挂重物．当弹簧伸长x 0，
重物在O 处达到平衡，现取重物在O 处时各种势能均为零，则当弹簧长度为原长时，系统的重力势能为_ ____；系统的弹性势能为 ；系统的总势能为 ． （答案用k 和x 0表示）
三. 计算题：
27．如图4-28所示，质量m 为 0.1 kg 的木块，在一个水平面上和一个劲度系数k 为20 N/m 的轻弹簧碰撞，木块将弹簧由原长压缩了x = 0.4 m ．假设木块与水平面间的滑动摩擦系数μ k 为0.25，
问在将要发生碰撞时木块的速率v 为多少？
图4－27 习题4-23图
图4－28 习题4-27图
30．质量分别为m和M的两个粒子，最初处在静止状态，并且彼此相距无穷远．以后，由于万有引力的作用，它们彼此接近．求：当它们之间的距离为d时，它们的相对速度多大？
36．在一光滑水平面上，有一轻弹簧，一端固定，一端连接一质量m = 1 kg 的Array滑块，如图4-35所示．弹簧自然长度l0= 0.2 m，劲度系数k =100 N·m-1. 设t =
0时，弹簧长度为l0，滑块速度v0 = 5 m·s-1，方向与弹簧垂直．以后某一时刻，
弹簧长度l =0.5 m．求该时刻滑块速度v的大小和夹角θ ．
图4－35 习题4-36。