圆锥曲线单元小结

《圆锥曲线》知识要点及重要结论一、椭圆1定义 平面内到两定点 F 「F 2的距离的和等于常数 2a(2^|F^2)的点P 的轨迹叫做椭 圆•若2a = F ,F 2，点P 的轨迹是线段F I F 2・若0 ：：： 2a ：：： F ,F 2，点P 不存在•2 2务 与=1(a b 0)，两焦点为 R (_c,0), F 2(c,0). a b2 2=1(a b ■ 0)，两焦点为 F i (0,_c), F 2(0,C ).其中 a 2"2 cla b3几何性质椭圆是轴对称图形，有两条对称轴 .椭圆是中心对称图形，对称中心是椭圆的中心椭圆的顶点有四个，长轴长为2a ，短轴长为2b ，椭圆的焦点在长轴上•2 2若椭圆的标准方程为 务•与=1(a b ■ 0)，则- a 空x 空a, -b 曲乞b ； a b2 2若椭圆的标准方程为=1(a b 0)，则-b 辽x 乞b,-a y 乞a .a 2b 2二、双曲线1定义 平面内到两定点 F 1, F 2的距离之差的绝对值等于常数 2a(0 ：：： 2a ：：：R F ?)的点的轨迹叫做双曲线.若2^|F 1F 2，点P 的轨迹是两条射线.若2^|F 1F 2，点P 不存在.2 22 标准方程 务—£=1(a ■ 0,b0)，两焦点为 F 1(-c,0), F 2(C ,0).a b2 2令…占二“ 0,b 0)，两焦点为 F 1 (0^c ), F 2(0, c ).其中 c 2 二 a 2 b 2. a b3几何性质双曲线是轴对称图形，有两条对称轴；双曲线是中心对称图形，对称中心是双曲线的中心 双曲线的顶点有两个 A 1, A 2，实轴长为2a ，虚轴长为2b ，双曲线的焦点在实轴上2 2J 壬-1(a 0,b 0)，则 x 乞-a 或x — a, y R ；a b2-牛=1(a 0,b 0)，则 y — -a 或 y — a, x R .b 22标准方程 若双曲线的标准方程为 若双曲线的标准方程为2a4渐近线双曲线的渐进线是它的重要几何特征， 每一双曲线都对应确定双曲线的渐进线, 组渐进线却对应无数条双曲线 .2 2 2 2与双曲线 笃-与 "(a 0,b ■ 0)共渐进线的双曲线可表示为笃-笃二a ba b定要“消元后的方程的二次项系数=0”和“ .0”同时成5等轴双曲线：实轴长等于虚轴长的双曲线叫做等轴双曲线2 2 2 2等轴双曲线的标准方程为 笃一爲=1(a . 0)或爲-笃=1(a .0).a aa a等轴双曲线的渐近线方程为 y= x .6共轭双曲线：实轴为虚轴，虚轴为实轴的双曲线互为共轭双曲线2 2 2 2如：笃-Xr =1(a 0,b - 0)的共轭双曲线为 Xr =1(a 0,b - 0)，它们的焦点到 a b b ax 禾廿y = _ a三、抛物线1定义 平面内与一个定点 F 和一条定直线l(F 不在I 上)的距离相等的点的轨迹叫做抛物 线•定点F 叫做抛物线的焦点，定直线 I 叫做抛物线的准线• 2标准方程(1) y 2=2px(p>0)，焦点为(#,0)，准线方程为x =—号，抛物线张口向右.⑵ y 2- -2px(p0)，焦点为(-号,0)，准线方程为x =号，抛物线张口向左•⑶x 2=2py(p0)，焦点为 硝) ，准线方程为y = 一号，抛物线张口向上.⑷X 2 = -2 py (p 0)，焦点为 (0,诗) ，准线方程为y 二号，抛物线张口向下. 其中p 表示焦点到准线的距离. 3几何性质2 2 双曲线x y2-.2ab2 2yx 2.2 a b=1( a 0, b 0)有两条渐近线y=1( a 0, b 0)有两条渐近线y a a x 和yx .即b b 2 2 x y=02■ 2ab22yx2.2ab但对于同直线与双曲线有两个交点的条件,原点的距离相等，因而在以原点为圆心,..a 2 b 2为半径的圆上•且它们的渐近线都是双曲线抛物线是轴对称图形，有一条对称轴.若方程为『=2px(p .0)或y = _2px(p ■ 0),则对称轴是x 轴，若方程为x 2 =2py(p . 0)或x 2 =_2py(p 0)，则对称轴是y 轴.若抛物线方程为 2y = 2 px( p . 0)，则 x _ 0, y R . 若抛物线方程为 2y - -2 px( p - 0)，则 x _ 0, y R . 若抛物线方程为 x = 2 py( p . 0)，则 y _ 0,x R .若抛物线方程为 x = -2py (p 0)，则 y _ 0, x R .圆锥曲线的一些重要结论【几个重要结论】2 21已知椭圆 笃•与 "(a b 0)的两焦点为Fj-cQEgO)，P(x 0,y 0)为椭圆上一a b点，则 PF 」=J(x ° +c)2 +y ； = J(x ° +c)2 +b 2(1 —爭)ms 丿 丿cx 0 cx 0因为 一a 乞 x 0 乞 a ， -c 0 _ c,0 ：：： a -c 0a c ，aa所以 PF^-cx°+a .同理，PF 2 =2a — PF,| =a —绝.aa2 2已知双曲线 务-占-1(a 0,b 0)的左、右焦点分别为Fj-cQ), F 2(C ,0) ,P(x 0,y 0)为a b双曲线上一点，则PF 1， PF 2 = 也—aaa2 22椭圆 J 七=1(a b 0)的两焦点为F I ,F 2，P 为椭圆上一点，若• F 1PF 2 7，则 a bb 2 sin ： ’ 2 丄 b tan 1 cos ： 2解：根据椭圆的定义可得 PR + PF 2 =2a ①c X 。

高中数学圆锥曲线知识点总结5篇高中数学圆锥曲线知识点总结5篇教育的现代化和大众化是推进知识普及和人才培养的重要策略。

科学科研的公正性和透明度是科研活动的重要保障。

下面就让小编给大家带来高中数学圆锥曲线知识点总结，希望大家喜欢!高中数学圆锥曲线知识点总结11、向量的加法向量的加法满足平行四边形法则和三角形法则。

AB+BC=AC。

a+b=(x+x ，y+y )。

a+0=0+a=a。

向量加法的运算律：交换律：a+b=b+a;结合律：(a+b)+c=a+(b+c)。

2、向量的减法如果a、b是互为相反的向量，那么a=-b，b=-a，a+b=0. 0的反向量为0 AB-AC=CB. 即“共同起点，指向被减”a=(x,y) b=(x ,y ) 则 a-b=(x-x ,y-y ).3、数乘向量实数λ和向量a的乘积是一个向量，记作λa，且∣λa∣=∣λ∣·∣a∣。

当λ 0时，λa与a同方向;当λ 0时，λa与a反方向;当λ=0时，λa=0，方向任意。

当a=0时，对于任意实数λ，都有λa=0。

注：按定义知，如果λa=0，那么λ=0或a=0。

实数λ叫做向量a的系数，乘数向量λa的几何意义就是将表示向量a的有向线段伸长或压缩。

当∣λ∣ 1时，表示向量a的有向线段在原方向(λ 0)或反方向(λ 0)上伸长为原来的∣λ∣倍;当∣λ∣ 1时，表示向量a的有向线段在原方向(λ 0)或反方向(λ 0)上缩短为原来的∣λ∣倍。

数与向量的乘法满足下面的运算律结合律：(λa)·b=λ(a·b)=(a·λb)。

向量对于数的分配律(第一分配律)：(λ+μ)a=λa+μa.数对于向量的分配律(第二分配律)：λ(a+b)=λa+λb.数乘向量的消去律：① 如果实数λ≠0且λa=λb，那么a=b。

② 如果a≠0且λa=μa，那么λ=μ。

4、向量的的数量积定义：两个非零向量的夹角记为〈a，b〉，且〈a，b〉∈[0，π]。

圆锥曲线知识点总结6篇第1篇示例：圆锥曲线是解析几何学中非常重要的概念，它们分为三种：椭圆、双曲线和抛物线。

在数学中，圆锥曲线具有丰富的性质和应用，掌握其基本知识对于理解其在几何、物理、工程等多个领域的应用至关重要。

本文将对圆锥曲线的基本性质和特点进行详细总结。

我们从圆锥曲线的定义入手。

圆锥曲线是平面上一点到一个固定点（焦点）和一条直线（准线）的距离之比为常数的点的轨迹。

根据这个定义，椭圆的准线是实直线，双曲线的准线是虚直线，而抛物线的准线是平行于其自身的直线。

椭圆是圆锥曲线中最简单的一种。

椭圆的定义是到焦点和准线的距离之比小于1的点构成的轨迹。

椭圆具有对称性，其焦点到准线的垂直距离之和恒等于两焦距之和，这个性质被称为焦点定理。

椭圆还有面积、周长等重要性质，在几何中有重要的应用。

抛物线是圆锥曲线中最特殊的一种，其定义是到焦点和准线的距离相等的点构成的轨迹。

抛物线具有对称性，其焦点到准线的垂直距离恰好等于焦距。

抛物线是一种非常重要的曲线，常见于物理学和工程学中的抛物线运动、光学、无线电通信等领域。

除了上述基本性质外，圆锥曲线还有许多重要的定理和性质。

焦点、准线、焦距、离心率等概念是理解圆锥曲线的重要基础。

圆锥曲线的方程形式也是研究和应用圆锥曲线的关键，椭圆和双曲线的标准方程分别为x^2/a^2 + y^2/b^2 = 1和x^2/a^2 - y^2/b^2 = 1，而抛物线的标准方程为y^2 = 2px。

圆锥曲线是解析几何学中的重要内容，掌握其基本性质和定理对于理解几何学、物理学和工程学中的问题有重要意义。

通过对圆锥曲线的学习，我们不仅可以深入理解几何形体的性质，还可以应用圆锥曲线的知识解决实际问题，提高数学建模和问题求解的能力。

加强对圆锥曲线知识的学习和应用是十分必要的。

第2篇示例：圆锥曲线是解析几何中最重要的一类曲线，它包括椭圆、双曲线和抛物线这三种。

这些曲线在数学和物理学等领域中有着重要的应用，是我们熟悉的常见数学概念之一。

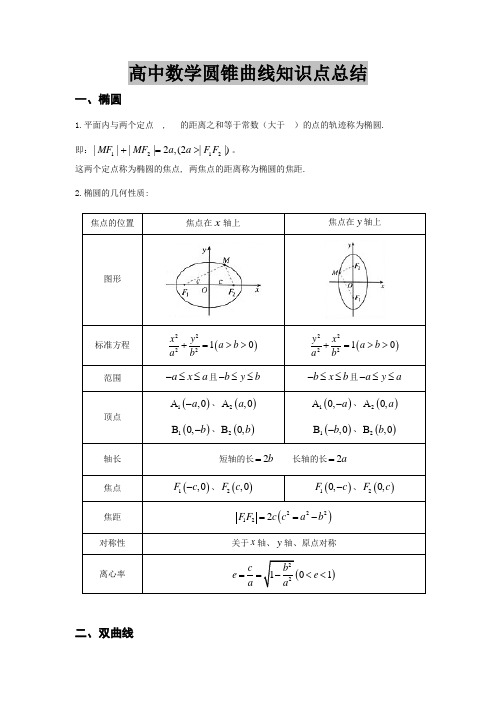
高中数学圆锥曲线知识点总结一、椭圆1.平面内与两个定点 , 的距离之和等于常数（大于 ）的点的轨迹称为椭圆. 即：|)|2(,2||||2121F F a a MF MF >=+。

这两个定点称为椭圆的焦点, 两焦点的距离称为椭圆的焦距.2.椭圆的几何性质:焦点的位置焦点在x 轴上焦点在y 轴上图形标准方程()222210x y a b a b +=>> ()222210y x a b a b+=>> 范围a x a -≤≤且b y b -≤≤ b x b -≤≤且a y a -≤≤顶点()1,0a A -、()2,0a A()10,b B -、()20,b B()10,a A -、()20,a A ()1,0b B -、()2,0b B轴长 短轴的长2b = 长轴的长2a =焦点 ()1,0F c -、()2,0F c ()10,F c -、()20,F c焦距 ()222122F F c c a b ==-对称性 关于x 轴、y 轴、原点对称离心率 ()22101c b e e a a==-<<二、双曲线1.平面内与两个定点 , 的距离之差的绝对值等于常数（小于 ）的点的轨迹称为双曲线. 即： 。

这两个定点称为双曲线的焦点, 两焦点的距离称为双曲线的焦距．2.双曲线的几何性质:焦点的位置焦点在x 轴上焦点在y 轴上图形标准方程()222210,0x y a b a b-=>> ()222210,0y x a b a b-=>> 范围 或 ,或 ,顶点 ()1,0a A -、()2,0a A ()10,a A -、()20,a A轴长 虚轴的长2b = 实轴的长2a =焦点 ()1,0F c -、()2,0F c ()10,F c -、()20,F c焦距 ()222122F F c c a b ==+对称性关于 轴、 轴对称, 关于原点中心对称离心率()2211c b e e a a==+>渐近线方程b y x a=±a y x b=±3.等轴双曲线: 双曲线 称为等轴双曲线, 其渐近线方程为 , 离心率 . 4、共渐近线的双曲线系方程:三、抛物线1.平面内与一个定点 和一条定直线 的距离相等的点的轨迹称为抛物线. 定点 称为抛物线的焦点, 定直线 称为抛物线的准线.2.抛物线的几何性质:标准方程22y px =()0p >22y px =- ()0p > 22x py = ()0p > 22x py =-()0p >图形顶点()0,0对称轴x 轴y 轴焦点,02p F ⎛⎫⎪⎝⎭ ,02p F ⎛⎫- ⎪⎝⎭0,2p F ⎛⎫ ⎪⎝⎭0,2p F ⎛⎫- ⎪⎝⎭准线方程2px =-2p x =2p y =-2p y =离心率 1e =范围0x ≥ 0x ≤0y ≥ 0y ≤3.过抛物线的焦点作垂直于对称轴且交抛物线于 、 两点的线段 , 称为抛物线的“通径”, 即 .4.焦半径公式:若点 在抛物线 上, 焦点为 , 则 ； 若点 在抛物线 上, 焦点为 , 则 ； 5、焦点弦: = +p四、圆1.定义: 点集｛M ｜｜OM ｜=r ｝, 其中定点O 为圆心, 定长r 为半径.2.方程: (1)标准方程: 圆心在c(a,b), 半径为r 的圆方程是(x-a)2+(y-b)2=r2圆心在坐标原点, 半径为r 的圆方程是x2+y2=r2(2)一般方程: ①当D2+E2-4F ＞0时, 一元二次方程x2+y2+Dx+Ey+F=0叫做圆的一般方程, 圆心为 半径是 。

圆锥曲线知识点总结圆锥曲线是高中数学中的重要内容，包括椭圆、双曲线和抛物线。

掌握圆锥曲线的相关知识对于解决数学问题和理解数学的应用具有重要意义。

一、椭圆1、定义平面内与两个定点 F1、F2 的距离之和等于常数（大于|F1F2|）的点的轨迹叫做椭圆。

这两个定点叫做椭圆的焦点，两焦点间的距离叫做焦距。

2、标准方程（1）焦点在 x 轴上：＼（＼frac{x^2}｛a^2} ＋＼frac{y^2}｛b^2} ＝ 1\）（＼（a ＞ b ＞ 0\）），其中\（a\）为长半轴长，＼（b\）为短半轴长，＼（c\）为半焦距，满足\（c^2 ＝ a^2 b^2\）。

（2）焦点在 y 轴上：＼（＼frac{y^2}｛a^2} ＋＼frac{x^2}｛b^2} ＝ 1\）（＼（a ＞ b ＞ 0\））。

3、椭圆的性质（1）对称性：椭圆关于 x 轴、y 轴和原点对称。

（2）范围：＼（a ＼leq x ＼leq a\），＼（b ＼leq y ＼leq b\）。

点为\（（＼pm a, 0)＼），＼（（0, ＼pm b)＼）；焦点在 y 轴上时，顶点为\（（0, ＼pm a)＼），＼（（＼pm b, 0)＼）。

（4）离心率：椭圆的离心率\（e ＝＼frac{c}｛a}＼）（＼（0 ＜ e ＜ 1\）），它反映了椭圆的扁平程度，＼（e\）越接近 0，椭圆越接近于圆；＼（e\）越接近 1，椭圆越扁。

二、双曲线1、定义平面内与两个定点 F1、F2 的距离之差的绝对值等于常数（小于|F1F2|）的点的轨迹叫做双曲线。

这两个定点叫做双曲线的焦点，两焦点间的距离叫做焦距。

2、标准方程（1）焦点在 x 轴上：＼（＼frac{x^2}｛a^2} ＼frac{y^2}｛b^2} ＝1\），其中\（a\）为实半轴长，＼（b\）为虚半轴长，＼（c\）为半焦距，满足\（c^2 ＝ a^2 ＋ b^2\）。

（2）焦点在 y 轴上：＼（＼frac{y^2}｛a^2} ＼frac{x^2}｛b^2} ＝1\）。

完整版)圆锥曲线知识点归纳总结1.圆锥曲线的定义和构造圆锥曲线是在平面上由一个固定点（焦点）和一个固定直线（准线）决定的点集。

三种经典的圆锥曲线分别为椭圆、抛物线和双曲线。

构造圆锥曲线需要确定焦点和准线的位置以及确定参数值。

2.椭圆的特性椭圆是圆锥曲线中最常见的一种形式，由两个焦点和一个大于等于焦距的参数决定。

椭圆的离心率小于1，且离心率等于焦点到准线的距离除以准线长度。

椭圆的焦缩比为焦点到椭圆上某一点的距离与该点到准线的距离的比值。

重要公式：椭圆的标准方程为(x^2/a^2) + (y^2/b^2) = 1；焦缩比为e = c/a，其中c^2 = a^2 – b^2.3.抛物线的特性抛物线是圆锥曲线中的一种形式，由一个焦点和一个参数决定。

抛物线的离心率为1，焦缩比为1.抛物线的轴是准线，顶点是焦点和准线的交点。

重要公式：抛物线的标准方程为(x^2/4a) = y。

4.双曲线的特性双曲线是圆锥曲线中的一种形式，由两个焦点和一个焦距决定。

双曲线的离心率大于1，离心率等于焦点到准线的距离除以准线长度。

双曲线的焦缩比为c^2 = a^2 + b^2.重要公式：双曲线的标准方程为(x^2/a^2) – (y^2/b^2) = 1.5.圆锥曲线的应用圆锥曲线在数学和物理学中都有广泛的应用。

椭圆的应用包括轨道运动、天体力学以及密码学等领域。

抛物线的应用包括抛物面反射器、人工卫星的轨道设计等。

双曲线的应用包括电磁波的传播、双曲线钟的标定等。

6.圆锥曲线的性质圆锥曲线有许多共同的性质，如对称性、切线性质和焦点性质等。

对称性：椭圆和双曲线关于x轴和y轴都有对称性，抛物线关于y轴有对称性。

切线性质：圆锥曲线上任意一点的切线与焦点到该点的连线垂直。

焦点性质：圆锥曲线上的任意一点到焦点的距离与焦缩比成正比。

此文档总结了圆锥曲线的定义、特性、应用和性质等重要知识点，并提供了相关公式和图示。

熟悉了这些知识后，我们可以更加深入地理解和应用圆锥曲线的概念。

《圆锥曲线》知识要点及重要结论一、椭圆1 定义 平面内到两定点21,F F 的距离的和等于常数)2(221F F a a >的点P 的轨迹叫做椭圆。

若212F F a =，点P 的轨迹是线段21F F 。

若2120F F a <<，点P 不存在.2 标准方程 )0(12222>>=+b a b y a x ,两焦点为)0,(),0,(21c F c F -.)0(12222>>=+b a b x a y ,两焦点为),0(),,0(21c F c F -.其中222c b a +=. 3 几何性质椭圆是轴对称图形，有两条对称轴. 椭圆是中心对称图形,对称中心是椭圆的中心. 椭圆的顶点有四个，长轴长为a 2，短轴长为b 2，椭圆的焦点在长轴上。

若椭圆的标准方程为)0(12222>>=+b a b y a x ,则b y b a x a ≤≤-≤≤-,；若椭圆的标准方程为)0(12222>>=+b a b x a y ，则a y a b x b ≤≤-≤≤-,。

二、双曲线1 定义 平面内到两定点21,F F 的距离之差的绝对值等于常数)20(221F F a a <<的点的轨迹叫做双曲线. 若212F F a =，点P 的轨迹是两条射线.若212F F a >，点P 不存在.2 标准方程 )0,0(12222>>=-b a b y a x ，两焦点为)0,(),0,(21c F c F -。

)0,0(12222>>=-b a b y a x ，两焦点为),0(),,0(21c F c F -.其中222b a c +=. 3 几何性质双曲线是轴对称图形，有两条对称轴；双曲线是中心对称图形,对称中心是双曲线的中心。

双曲线的顶点有两个21,A A ,实轴长为a 2,虚轴长为b 2，双曲线的焦点在实轴上.若双曲线的标准方程为)0,0(12222>>=-b a by a x ，则R y a x a x ∈≥-≤,或；若双曲线的标准方程为)0,0(12222>>=-b a bx a y ，则R x a y a y ∈≥-≤,或。

电子版圆锥曲线知识点总结一、圆锥曲线的定义圆锥曲线是指平面上的一类曲线，可以由一个锥面上的一个圆截面和一个平面上的直线交点轨迹来定义。

根据这个定义，圆锥曲线可以分为椭圆、双曲线和抛物线三种类型。

1. 椭圆：椭圆是一个闭合曲线，其定义是一个平面上的动点的轨迹，该动点到两个给定点的距离之和等于一个常数。

椭圆的特点是对称性明显，轴对称和中心对称的性质。

2. 双曲线：双曲线是一个开口向上或向下的曲线，其定义是一个平面上的点的轨迹，该点到两个给定点的距离之差等于一个常数。

双曲线的特点是具有两个分支，分支之间存在对称性。

3. 抛物线：抛物线是一个开口朝上或朝下的曲线，其定义是一个平面上的动点的轨迹，该点到一个给定点的距离等于到一个给定直线的距离。

抛物线的特点是对称性明显，经常出现在物体飞行轨迹和抛射物的运动中。

二、圆锥曲线的方程圆锥曲线的方程是解析几何中的重要内容，可以通过不同的方式来表示。

根据圆锥曲线的类型，其方程也有所不同。

1. 椭圆的方程：椭圆的标准方程是(x/a)² + (y/b)² = 1，其中a和b分别是椭圆的长轴和短轴。

2. 双曲线的方程：双曲线的标准方程是(x/a)² - (y/b)² = 1或者(y/b)² - (x/a)² = 1，其中a和b分别是双曲线的长轴和短轴。

3. 抛物线的方程：抛物线的标准方程是(x/h)² = 4py或者(y/k)² = 4px，其中p是焦点到准线的距离，h和k分别是抛物线的横轴和纵轴的顶点坐标。

三、圆锥曲线的性质圆锥曲线具有许多重要的性质，这些性质不仅可以帮助我们理解和描述曲线的形状，还可以在具体问题中进行应用。

1. 直线的切线性质：圆锥曲线在不同位置都有切线，而且其切线和曲线在切点处相切，且切线的斜率由曲线的斜率表达。

2. 曲线的离心率：离心率是描述圆锥曲线形状的一个重要参数，表示曲线长轴和短轴之间的比值。

《圆锥曲线》知识要点及重要结论、椭圆1定义 平面内到两定点 F 「F 2的距离的和等于常数2a(2^|F^2)的点P 的轨迹叫做椭圆•若2a = F ,F 2，点P 的轨迹是线段F I F 2・若0 ：：： 2a ：：： F ,F 2，点P 不存在•2 2务 与=1(a b 0)，两焦点为 R (_c,0), F 2(c,0). a b2 2X2 =1(ab ■ 0)，两焦点为 F i (0,_c), F 2(0,C ).其中 a 2"2 cla b3几何性质椭圆是轴对称图形，有两条对称轴 .椭圆是中心对称图形，对称中心是椭圆的中心椭圆的顶点有四个，长轴长为2a ，短轴长为2b ，椭圆的焦点在长轴上•2 2若椭圆的标准方程为 务•与=1(a b ■ 0)，则- a 空x 空a, -b 曲乞b ； a b2 2若椭圆的标准方程为 =1(a b 0)，则-b 辽x 乞b,-a y 乞a .a 2b 2二、双曲线1定义 平面内到两定点 F 1, F 2的距离之差的绝对值等于常数 2a(0 ：：： 2a ：：：R F ?)的点的轨迹叫做双曲线.若2^|F 1F 2，点P 的轨迹是两条射线.若2^|F 1F 2，点P 不存在.2 22 标准方程务 一―1(a ■ 0,b0)，两焦点为 F 1(-c,0), F 2(C ,0).a b2 2令…占二“ 0,b 0)，两焦点为 F 1 (0^c ), F 2(0, c ).其中 c 2 二 a 2 b 2. a b 3几何性质双曲线是轴对称图形，有两条对称轴；双曲线是中心对称图形，对称中心是双曲线的中心 双曲线的顶点有两个 A 1, A 2，实轴长为2a ，虚轴长为2b ，双曲线的焦点在实轴上2 2J 壬-1(a 0,b 0)，则 x 乞-a 或x — a, y R ；a b2-牛=1(a 0,b 0)，则 y — -a 或 y — a, x R .b 22标准方程 若双曲线的标准方程为 若双曲线的标准方程为2a4渐近线双曲线的渐进线是它的重要几何特征， 每一双曲线都对应确定双曲线的渐进线， 但对于同组渐进线却对应无数条双曲线 •2 2 2 2与双曲线 笃-与 "(a 0,b ■ 0)共渐进线的双曲线可表示为 笃一笃=，(・=0).a ba b直线与双曲线有两个交点的条件，一定要“消元后的方程的二次项系数 同时成立•5等轴双曲线：实轴长等于虚轴长的双曲线叫做等轴双曲线•2 2 2 2等轴双曲线的标准方程为 务一爲=1(a . 0)或爲-笃 "(a ■ 0).a aa a等轴双曲线的渐近线方程为 y =「x .6共轭双曲线：实轴为虚轴，虚轴为实轴的双曲线互为共轭双曲线2 2 2 2如：笃-与=1(a0,b - 0)的共轭双曲线为 每-务=1(a0,b - 0)，它们的焦点到a bb a原点的距离相等，因而在以原点为圆心，.a 2 b 2为半径的圆上.且它们的渐近线都是b b y x 和 y x .aa三、抛物线1定义 平面内与一个定点 F 和一条定直线l(F 不在I 上)的距离相等的点的轨迹叫做抛物 线.定点F 叫做抛物线的焦点，定直线 I 叫做抛物线的准线. 2标准方程(1) y 2 =2px(p 0)，焦点为(号,0)，准线方程为x = -号，抛物线张口向右.⑵y 2 =-2px(p 0)，焦点为(-p,0)，准线方程为x =号，抛物线张口向左.⑶x 2 =2py (p 0)，焦点为 (0导 ，准线方程为y = 一号，抛物线张口向上.⑷X 2 - -2 py (p 0)，焦点为 (0』) ，准线方程为y = _p ，抛物线张口向下. 其中p 表示焦点到准线的距离. 3几何性质抛物线是轴对称图形，有一条对称轴.若方程为y 2 = 2 px( p - 0)或y 2 = -2 px( p - 0)，2 2双曲线x y2 -.2ab2 2yx 2.2 a b=1(a 0, b 0)有两条渐近线y=1( a 0, b 0)有两条渐近线y a a x 和yx .即b b 2 2x y=02■ 2ab22yx2.2ab=0” 和“二.0双曲线则对称轴是x 轴，若方程为x 2 =2py(p . 0)或x 2 =_2py(p 0)，则对称轴是y 轴.若抛物线方程为y 2 =2 px( p 0)，则x 亠0, y 尸R . 若抛物线方程为y 2 - -2 px( p .0)，则x _ 0, y• R .2若抛物线方程为x =2py(p . 0)，则y_0,x ・R . 若抛物线方程为x 2 - -2 py( p .0)，贝V y 込0, x 三R .圆锥曲线的一些重要结论【几个重要结论】2 21已知椭圆 笃•与 "(a b 0)的两焦点为F !^c,0),F 2(c,0)，P(x °,y °)为椭圆上一a b点，则I PF.H c)*2冷冷心讪1一予)ms 丿 丿cx 0 cx 0因为 一a _ x 0 _ a ， -c 仝乞 c,0 ：：： a -c 0 a c ，aa所以 |PF^-cx ° +a .同理，PF 2 =2a — PF,| =a —也.a a. b sin a 2a L F!PF 2的面积为b tan .1 +cos^2解：根据椭圆的定义可得|PF_, +|PF 2| =2a ①由余弦定理可得 4c 2 = F J F 2 2 =|PFj 2 +|PF 2 2 — 2PF 」PF 2 COS 。

高中圆锥曲线结论总结
高中圆锥曲线结论总结
一、圆锥曲线的标准方程
圆锥曲线的标准方程为：
$$frac{x^2}{a^2}+frac{y^2}{b^2}=1$$
其中，a与b分别是椭圆的两个半径，且ab，a与b是正实数。

二、圆锥曲线的性质
1. 圆锥曲线的概念
圆锥曲线是由两个椭圆及其余部分所构成的四边形的边界线，是圆锥曲线的概念。

2. 圆锥曲线的对称性
由于圆锥曲线是由两个椭圆所构成，因此它具有x轴对称性和y 轴对称性，即曲线的俩边彼此对称。

3. 圆锥曲线的四个焦点
圆锥曲线的四个焦点分别位于椭圆的两个长轴端点，称为四个焦点。

4. 圆锥曲线的两个长轴
圆锥曲线的两个长轴是两个椭圆的长轴，它们的长度分别是a和b，两轴相交处的位置是圆锥曲线的中心点。

5. 圆锥曲线的弧长
圆锥曲线的弧长为：
$$mathcal{L}=2aarcsinfrac{b}{a}$$
其中，a与b是椭圆的两个半径，且ab。

6. 圆锥曲线的曲率
圆锥曲线的曲率为：
$$K=frac{a}{b}$$
其中，a与b是椭圆的两个半径，且ab。