六年级(正反比例)练习卷

一、判断题：1、圆的面积和圆的半径成正比例。

（）2、圆的面积和圆的半径的平方成正比例。

（）3、圆的面积和圆的周长的平方成正比例。

（）4、正方形的面积和边长成正比例。

（）5、正方形的周长和边长成正比例。

（）6、长方形的面积一定时，长和宽成反比例。

（）7、长方形的周长一定时，长和宽成反比例。

（）8、三角形的面积一定时，底和高成反比例。

（）9、梯形的面积一定时，上底和下底的和与高成反比例。

（）10、圆根据规律判断比例关系，并填空。

的周长和圆的半径成正比例。

（）二．看图表填空X 2 3 5 10 ……Y 4.5 7.5 12 ……（1）X与Y( ) A. 成正比例 B. 成反比例。

X 2 3 5 10 ……Y 4 2.4 12 ……（2）X与Y( ) A. 成正比例 B. 成反比例。

三．判断对错（1）路程一定，速度和时间成正比例。

（）（2）一堆煤的总量不变，烧去的煤与剩下的煤成反比例。

（）（3）花生的出油率一定，花生的重量与榨出花生油的重量成正比例。

（）（4）平行四边形的面积不变，它的底与高成反比例。

（）（5）正方体的表面积与体积成正比例。

（）（6）一堆煤的总量不变，每天烧去的数量与烧的天数成反比例。

（）（7）长方体底面积一定，体积和高成正比例。

（）（8）三角形的面积不变，它的底与高成反比例。

（）一．选择填空，判断数量间的比例关系。

A、成正比例 B、成反比例 C、不成比例（1）比例尺一定，图上距离与实际距离____________。

（2）圆的面积一定，直径与圆周率_______________。

（3）比的前项一定，比的后项与比值_________________。

（4）时间一定，速度与路程____________。

（5）被减数一定，减数与差______________。

（6）圆锥体体积一定，底面积与高_____________。

二、下列各题中的两种量是不是成比例，成什么比例，并说明理由。

（1）买相同的电脑，购买的电脑台数与总价（2）小明的年龄和体重（3）总路程一定，已行的路程与未行的路程（4）分数值一定，分数的分子与分母（5）圆的面积和半径（6）长方体的体积一定，底面积和高（7）正方体的表面积和底面积（8）圆的周长一定，圆周率和直径（9）订阅《扬子晚报》，订的份数与总价（10）小麦的出粉率一定，小麦的质量与面粉的质量。

正反比例练习题六年级一、判断题1. 如果两个变量的比值一定，那么这两个变量成正比例。

2. 两个量的乘积一定时，这两个量成反比例。

3. 物体行驶的速度与行驶的时间成反比例。

4. 成本和数量成正比例。

5. 一个数与它的倒数的乘积为1，所以一个数与它的倒数成反比例。

二、选择题1. 下列哪个关系成正比例？A. 圆的半径和面积B. 物体的质量和体积C. 路程和时间D. 圆的周长和直径2. 下列哪个关系成反比例？A. 单价和总价B. 速度和时间C. 工作效率和工作量D. 路程和速度三、填空题1. 如果两个变量成正比例，那么它们的比值是______。

2. 如果两个变量成反比例，那么它们的乘积是______。

3. 在平面直角坐标系中，正比例函数的图像是一条经过______的直线。

4. 在平面直角坐标系中，反比例函数的图像是______双曲线。

5. 一个长方形的面积是30平方厘米，如果长和宽成反比例，那么当长为6厘米时，宽为______厘米。

四、应用题1. 某品牌手机充电器输出电压为5V，充电电流为1A。

请问充电器的功率是多少？2. 小明骑自行车去图书馆，路程为8公里，速度为4公里/小时。

请问小明骑车去图书馆需要多长时间？3. 某商品的单价是50元，如果购买5件可以享受8折优惠。

请问购买5件商品的总价是多少？4. 一个水池，每小时进水量为30立方米，出水口每小时出水20立方米。

请问经过5小时，水池中的水增加了多少立方米？5. 某班学生平均分为80分，其中最高分为95分。

如果将最高分改为100分，平均分将变为多少？五、计算题1. 已知正方形的周长是24厘米，求正方形的面积。

2. 一个数的2倍与它的3倍的和是60，求这个数。

3. 某数是它的1/3加上5，求这个数。

4. 一个长方形的长是宽的2倍，如果宽是6厘米，求长方形的面积。

5. 某人用每千克5元的价格购买了若干千克的苹果，总共花费了25元，求购买的苹果重量。

六、作图题1. 在方格纸上画出一个正比例函数的图像，其比例系数为2。

正比例反比例练习题正反比例练题一、选择、填空。

1、如果3a=4b，那么a∶b＝（）。

A、3∶4B、4∶3C、3a∶4b2、下面不成比例的是()。

A、正方形的周长和边长。

B、某同学从家到学校的步行速度和所用时间。

C、圆的体积和表面积。

3、下列各式中（a、b均不为），a和b成反比例的是（）。

A、a×8＝b5B、9a＝6bC、a×13 －1÷b= 0D、a＋710＝b4、如果y=15x,x和y成()比例；如果y=15/x,x和y成()比例。

5、如果Y = 8X，X和Y成（）比例；如果Y = 8/X，X和Y成（）比例。

348、在一个比例式中，两个外项的积是最小的质数，其中一个内项是3，另一个外项是（）。

9、相遇问题，时间一定，速度和路程成（）比例。

如果甲、乙两车的速度比是7：9，相遇时，甲、乙两车行过的路程比是（）。

10、货车的速度是客车的40%。

货、客两车同时从甲、乙两地相向而行，经过2小时相遇。

相遇时，货车与客车行过的路程的比是（）：（）。

11、假如x÷y=712×2，那末x和XXX（）比例；假如x:4=5:y，那末x和XXX（）比例。

12、圆的半径与圆周长（）。

A、成正比例B、成反比例C、不成比例D、没有关系13、互为倒数的两个数，它们一定成（）。

A、正比例B、反比例C、不成比例D、无法判断14、小王的身高与体重成（）。

A、正比例B、反比例C、不成比例D、没法判断15、总时间一定，要制造的零件总数和制造每个零件所用的时间成（）比例．16、两个齿轮啮合转动时转速和齿数成（）比例．．17、房间面积一定，每块地板砖的面积与用砖的块数成（）比例．．18、汽车行驶时每公里的耗油量一定，所行驶的距离和耗油总量成（）比例．．19、糖水的重量一定,糖的重量和水的重量成()比例．20、大豆的出油率一定，大豆的数量和出油的数量成（）比例21、总是相等的两个量成（）比例．二、判断。

一、选择题（每题2分，共20分）1. 下列哪个图形不是正比例图形？A. 正方形B. 长方形C. 平行四边形D. 矩形2. 下列哪个关系是反比例关系？A. 长方形的面积与长B. 长方形的面积与宽C. 长方形的周长与长D. 长方形的周长与宽3. 两个数的乘积是24，如果其中一个数是4，那么另一个数是：A. 6B. 3C. 8D. 24. 一辆汽车以60千米/小时的速度行驶，行驶了2小时，汽车行驶的距离是：A. 120千米B. 90千米C. 180千米D. 300千米5. 一个比例关系为2：4=3：x，那么x的值是：A. 6B. 8C. 12D. 166. 小华有15本书，如果每天看3本，看几天可以看完？A. 5天B. 4天C. 3天D. 2天7. 一辆自行车每小时行驶15千米，行驶了3小时，自行车行驶的距离是：A. 45千米B. 30千米C. 60千米D. 90千米8. 两个数的和是20，如果其中一个数是5，那么另一个数是：A. 15B. 10C. 20D. 259. 一块长方形菜地的长是40米，宽是20米，这块菜地的面积是：A. 400平方米B. 800平方米C. 1600平方米D. 3200平方米10. 一个比例关系为5：10=1：x，那么x的值是：A. 2B. 3C. 5D. 10二、填空题（每题2分，共20分）11. 如果一个数的3倍是12，那么这个数是______。

12. 一个长方形的长是8厘米，宽是4厘米，这个长方形的周长是______厘米。

13. 两个数的比是3：5，如果其中一个数是15，那么另一个数是______。

14. 一辆自行车每小时行驶20千米，行驶了4小时，自行车行驶的距离是______千米。

15. 一辆汽车以80千米/小时的速度行驶，行驶了5小时，汽车行驶的距离是______千米。

16. 一个比例关系为6：12=2：x，那么x的值是______。

17. 一个长方形的长是12厘米，宽是6厘米，这个长方形的面积是______平方厘米。

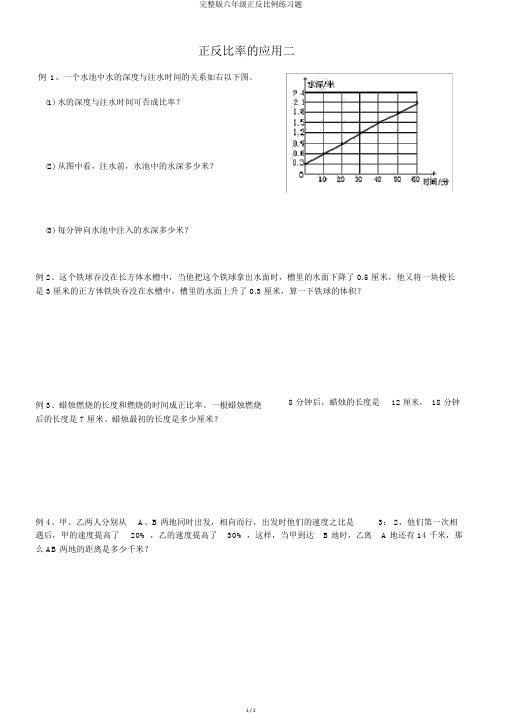
正反比率的应用二例1、一个水池中水的深度与注水时间的关系如右以下图。

(1)水的深度与注水时间可否成比率？(2)从图中看，注水前，水池中的水深多少米？(3)每分钟向水池中注入的水深多少米？例 2、这个铁球吞没在长方体水槽中，当他把这个铁球拿出水面时，槽里的水面下降了 0.5 厘米，他又将一块棱长是 3 厘米的正方体铁块吞没在水槽中，槽里的水面上升了 0.3 厘米，算一下铁球的体积？例 3、蜡烛燃烧的长度和燃烧的时间成正比率。

一根蜡烛燃烧后的长度是 7 厘米。

蜡烛最初的长度是多少厘米？8 分钟后，蜡烛的长度是12 厘米，18 分钟例 4、甲、乙两人分别从A、B 两地同时出发，相向而行，出发时他们的速度之比是遇后，甲的速度提高了20% ，乙的速度提高了30% ，这样，当甲到达 B 地时，乙离3： 2，他们第一次相A 地还有 14 千米，那么 AB 两地的距离是多少千米？看看你会做吗？1、用不相同的杯子装水，水的高度与杯子的底面积的关系如右图。

（ 1）从图中看，水的高度与杯子的底面积可否成比率？成什么比率？为什么？（ 2）从图中估计，当杯子的底面积是50 平方厘米时，水深多少厘米？当水深25 厘米时，杯子的底面积是多少平方厘米？2、将一个圆柱体完好吞没在一个装满水的水槽中，拿出后水面下降了9 厘米。

尔后放入一个底面积和圆柱体相同，高是圆柱体1的圆锥，这时水面会上升多少厘米？23、蜡烛燃烧的长度和燃烧的时间成正比率。

一根蜡烛燃烧12 分钟后，蜡烛的长度是17 厘米， 18 分钟后的长度是 9 厘米。

蜡烛最初的长度是多少厘米？4、甲、乙两人分别从A、 B 两地同时出发，相向而行，出发时他们的速度之比是后，甲的速度提高了20% ，乙的速度提高了40% ，当甲到达目的地后，乙还有AB 两地的距离是多少千米？4： 3，他们第一次相遇44 千米到达目的地，那么。

完整)六年级正反比例练习题1.判断1.当一个因数不变时，它与另一个因数的积成正比例。

（√）2.当长方形的长一定时，宽和面积成正比例。

（√）3.当圆的半径增加时，周长也会增加，它们成正比例。

（√）4.当铺地面积一定时，方砖的边长和所需的块数成反比例。

（√）5.当铺地面积一定时，方砖的面积和所需的块数成反比例。

（√）6.当圆的半径增加时，面积也会增加，它们成正比例。

（√）7.当圆的半径增加时，面积和圆的半径的平方成正比例。

（√）8.当圆的半径增加时，面积和圆的周长的平方成正比例。

（√）9.当正方形的边长增加时，面积也会增加，它们成正比例。

（√）10.当正方形的边长增加时，周长也会增加，它们成正比例。

（√）11.当长方形的面积一定时，长和宽成反比例。

（√）12.当长方形的周长一定时，长和宽成反比例。

（√）13.当梯形的面积一定时，上底和下底的和与高成反比例。

（√）简单说明理由：1.路程一定，速度和时间成反比例，因为速度越快，用的时间越短，反之亦然。

2.车轮的直径一定，所行的路程和车轮的转数成正比例，因为车轮转数越多，所行的路程也就越长。

3.图上距离一定，实际距离和比例尺成正比例，因为比例尺越大，实际距离也就越长。

4.数A与它的倒数成反比例，因为它们的积始终为1.5.收入一定，支出和结余成反比例，因为支出越多，结余越少。

6.除数一定，被除数和商成正比例，因为被除数越大，商也就越大。

7.5A=3B，A和XXX反比例，因为B随着A的增加而减少。

8.总价一定，观看同一场电影的票价和人数成反比例，因为人数越多，每人分摊的票价也就越少。

9.三角形的面积和它的高成正比例，因为高越高，底边也就越长，面积也就越大。

10.长方形的周长一定，它的长和宽成反比例，因为长和宽的和越大，周长也就越大。

11.年龄和身高无法确定成比例关系，因为年龄和身高并没有必然的联系。

12.比例尺一定，图上距离和实际距离成正比例，因为比例尺越大，实际距离也就越长。

人教版六年级数学下册第四单元7．正比例和反比例一、仔细审题，填一填。

(每空2分，共12分) 1．如果x y ＝9.8，那么x 和y 成( )比例。

2．圆锥的体积一定，圆锥的底面积和高成( )比例；购买无人飞机的单价一定，总价和数量成( )比例。

3．已知mn ＝a (m 、n 、a 均不为0)，当a 一定时，m 和n 成( )比例；当m 一定时，n 和a 成( )比例；当n 一定时，m 和a 成( )比例。

二、火眼金睛，判对错。

(对的在括号里画“√”，错的画“×”)(每小题4分，共16分)1．正方体的表面积与体积成正比例。

( ) 2. 一堆煤的总质量不变，每天平均烧去的质量与烧的天数成反比例。

( )3．圆的面积和半径的平方成正比例。

( ) 4．同时、同地测量物体时，物高和影长成反比例。

( ) 三、仔细推敲，选一选。

(将正确答案的序号填在括号里)(每小题4分，共16分)1．小明从家里去学校，所需时间与所行速度( )。

A ．成正比例B ．成反比例C ．不成比例2．下列各组量中，成反比例关系的是( )。

A ．三角形面积一定，底和高B ．王师傅每周生产零件总数和每天生产零件的个数C ．50个口罩，已卖出的口罩个数和没卖的口罩个数D ．房间面积一定，每块瓷砖的边长和所需块数 3．表示x 和y 成正比例关系的式子是( )。

A ．x ＋y ＝5 B ．y ＝5x C ．yx ＝0D ．x y ＋3＝54．圆的周长与( )成正比例关系。

A ．圆的面积B ．圆的半径C ．圆周率四、按要求填表。

(每小题8分，共16分) 1．x 和y 成正比例关系。

x 6 1.5 3.6 y7.210.86.482．x 和y 成反比例关系。

x 2.5 0.5 13 y0.40.1255五、聪明的你，答一答。

(共40分) 1．把相同体积的水倒入底面积 不同的杯子中，杯子的底面 积和杯子中水面高度的关系 如图。

(1)杯子的底面积和水面高度成()比例关系。

用正反比例解决问题练习题一、填空1.一种盐水，是由盐和水按1:50 配制而成的。

其中，盐的重量占盐水的（），水的重量占盐水的（）。

2.一幅地图，图上A、B距离3厘米，地面上A、B距离150千米。

这幅图的比例尺是（）。

3.如果x÷y = 11×5，那么x和y成（）比例；如果x:4=5:y，那么x和y成（）比例。

4.如果甲÷乙=丙，那么，甲一定时，乙和丙成（）比例；乙一定时，甲和丙成（）比例；丙一定时，甲和乙成（）比例。

5.在比例尺为1:8的图纸上，甲、乙两圆的直径比是2:3，那么甲、乙两圆的实际的直径比是（）。

二、选择1.如果3x=8y（x、y都不等于0），那么x和y（）A、成正比例B、成反比例不成比例 D、以上说法都不对2.如果x3= y8（x、y都不等于0），那么x和y（）A、成正比例B、成反比例C、不成比例D、以上说法都不对3.下列表示x和y成反比例的式子是（）A、x+3y=12B、y=4xC、y=23x D、y=-32x4.已知kx=y，且x和y都不为0，当k一定时，x和y（）A、成正比例B、成反比例C、不成比例D、以上说法都不对5.甲数的34是乙数，那么甲数与乙数（）A、成正比例 B、成反比例C 、不成比例D 、以上说法都不对三、判断题1.正方形的边长和周长成正比例。

（ ）2.正方形的边长和面积成正比例。

（ ）3.a 是b 的57，数a 和数b 成正比例。

（ ）4.如果4a=3b,那么a ∶b=3∶4 。

（ ）5.A8= B ，那么A 和B 成反比例。

（ ）6.长方体的体积一定，底面积和高成反比例。

（ ）7.如果x 与y 成反比例，那么3 x 与y 也成反比例。

（ ）8.圆的面积与半径的平方成正比例。

（ ）9.圆锥的体积一定，底面积和高成反比例。

（ ） 10.全班总人数一定，出勤人数和出勤率成正比例。

（ ）四、根据比例关系填表1.根据yx=10，填写下表。

一、选择题（每题3分，共30分）1. 下列哪个图形的面积与边长不成比例？A. 正方形B. 长方形C. 矩形D. 圆2. 一个人以每小时5公里的速度匀速行驶，3小时后行驶了15公里，则此人行驶的速度与时间的关系是：A. 成正比例B. 成反比例C. 无关系D. 无法确定3. 下列哪个量的比值是固定的？A. 长方形的面积与长B. 正方形的周长与边长C. 圆的面积与半径D. 三角形的面积与底4. 一个长方形的周长是24厘米，如果长是8厘米，那么宽是：A. 4厘米B. 6厘米C. 8厘米D. 10厘米5. 两个数的积是12，一个数增加4，另一个数减少4，那么这两个数的和是：A. 8B. 10C. 12D. 166. 下列哪个函数图象是一条直线？A. y = 2x + 3B. y = 2x^2 + 1C. y = 2/xD. y = 2√x7. 一个正方形的周长比一个长方形的周长多8厘米，如果长方形的长是10厘米，那么正方形的边长是：A. 12厘米B. 14厘米C. 16厘米D. 18厘米8. 下列哪个关系式表示正比例？A. x + y = 10B. xy = 20C. x/y = 5D. x - y = 39. 两个数的和是18，一个数是5，那么另一个数是：A. 13B. 14C. 15D. 1610. 一个正方形的面积是16平方厘米，那么它的边长是：A. 2厘米B. 4厘米C. 8厘米D. 16厘米二、填空题（每题5分，共25分）11. 若x与y成正比例，则x/y的值为______。

12. 若x与y成反比例，则xy的值为______。

13. 一个数的3倍与另一个数的2倍相等，则这两个数的比值为______。

14. 一个长方形的面积是48平方厘米，长是8厘米，那么宽是______厘米。

15. 一个数的5倍加上12等于另一个数的3倍，那么这两个数的差是______。

三、解答题（每题10分，共30分）16. 小华骑自行车去图书馆，每小时行驶15公里，行驶了2小时后到达图书馆。

正反比例的练习题一、选择题1. 下列哪一项不是正比例关系？A. 速度与时间B. 路程与时间C. 面积与边长D. 体积与底面积2. 如果两个变量x和y满足y = kx（k为常数），则x和y之间的关系是：A. 反比例B. 正比例C. 非比例关系D. 无法确定3. 在反比例关系中，如果其中一个变量增加，另一个变量会：A. 增加B. 减少C. 保持不变D. 先增加后减少4. 已知A和B成正比例，当A增加时，B也会增加。

如果A的值从10增加到20，B的值从5增加到多少？A. 10B. 7.5C. 10D. 155. 某工厂的产量与工作时间成正比例关系，如果工作时间增加一倍，产量会：A. 减少B. 保持不变C. 增加一倍D. 增加两倍二、填空题6. 如果速度v（千米/小时）与时间t（小时）成反比例关系，那么它们的关系可以表示为________。

7. 某商品的单价为p元，数量为q个，总金额为m元，如果p和q成反比例关系，那么m与p的关系是________。

8. 已知x和y成正比例，x的值从2增加到4，y的值从3增加到6，那么x与y的比值k是________。

9. 在正比例关系中，如果变量A的值是变量B的两倍，那么变量B的值是变量A的________。

10. 某工厂的产量与机器数量成正比例关系，如果机器数量增加到原来的三倍，产量将________。

三、解答题11. 某工厂的产量与工作时间成正比例关系。

如果工作时间从8小时增加到12小时，产量从200件增加到多少件？（假设初始比例系数为25件/小时）12. 某城市的人口数量与人均收入成反比例关系，如果人均收入从2000元增加到3000元，人口数量从100万减少到多少？13. 已知某商品的单价p与销售量q成反比例关系，如果单价从10元降低到5元，销售量从1000件增加到多少？14. 某公司的总利润与销售量成正比例关系。

如果销售量从1000件增加到2000件，总利润从10万元增加到多少？15. 某学校的图书馆藏书数量与学生人数成反比例关系。