高一物理机械能守恒定律应用-连接体问题)
- 格式:ppt
- 大小:360.50 KB
- 文档页数:17




高中物理转盘连接体问题高中物理中的转盘连接体问题是指有两个或多个转盘通过轴连接在一起的物理问题。
这种问题一般涉及到力的传递、转动惯量和角加速度等概念。
下面将详细讨论该问题。
首先,我们来考虑两个转盘通过轴连接在一起的情况。
设转盘1的转动惯量为I₁,转盘2的转动惯量为I₂,通过轴连接的转动惯量为I₃。
假设外力作用在转盘1上,转盘2无外力作用。
根据动量守恒定律,外力对转盘1的扭矩τ₁等于转盘1的转动惯量I₁乘以角加速度α:τ₁ = I₁α₁根据转盘2的转动惯量和角加速度,可以得到转盘2的角加速度α₂:τ₂ = I₂α₂由于转盘1和转盘2通过轴连接在一起,因此它们的角加速度相等:α₁ = α₂ = α而两个转动物体的牵引力的作用点重合,所以τ₁ = τ₂,从而有:I₁α = I₂α由此得到:I₁α = I₂α(I₁ + I₂)α = 0当(I₁ + I₂) ≠ 0时,上式成立的唯一解是α = 0,即两个转盘的角加速度为0.这说明,当通过轴连接的转动惯量不为零时,两个转盘的角加速度相等且均为零,即它们将保持静止。
对于多个转盘通过轴连接在一起的情况,同样可以推导类似的结论。
假设第i个转盘的转动惯量为Iᵢ,通过轴连接的转动惯量为Iₙ,其中n为转盘的个数。
根据动量守恒定律和转动的叠加原理,可以得到:τ₁ + τ₂ + ... + τₙ = I₁α + I₂α + ... + Iₙα(I₁ + I₂ + ... + Iₙ)α = 0当(I₁ + I₂ + ... + Iₙ) ≠ 0时,上式成立的唯一解是α = 0,即所有转盘的角加速度为零。
这说明,当通过轴连接的转动惯量之和不为零时,所有转盘的角加速度均为零,它们将保持静止。
总结起来,转盘连接体问题中,通过轴连接的转动惯量之和为零时,转盘将保持静止;当转动惯量之和不为零时,转盘将保持静止。
这是由于转盘的转动惯量和角加速度之间存在一种固定的关系,通过轴连接的转动惯量之和可以看作是一个整体的转动惯量,在外力作用下,整体将保持静止。

微专题32机械能守恒定律在连接体问题中的应用【核心要点提示】机械能守恒定律理解的三种形式:1.守恒观点(1)表达式:E k1+E p1=E k2+E p2或E1=E2.(2)意义:系统初状态的机械能等于末状态的机械能.(3)注意:要先选取零势能参考平面,并且在整个过程中必须选取同一个零势能参考平面.2.转化观点(1)表达式:ΔE k=-ΔE p.(2)意义:系统的机械能守恒时,系统增加(或减少)的动能等于系统减少(或增加)的势能.3.转移观点(1)表达式:ΔE A增=ΔE B减.(2)意义:若系统由A、B两部分组成,当系统的机械能守恒时,则A部分机械能的增加量等于B部分机械能的减少量.【微专题训练】类型一:速率相等的连接体模型1.如图所示的两物体组成的系统,当释放B而使A、B运动的过程中,A、B的速度均沿绳子方向,在相等时间内A、B运动的路程相等,则A、B的速率相等。
2.判断系统的机械能是否守恒不从做功角度判断,而从能量转化的角度判断,即:如果系统中只有动能和势能相互转化,系统的机械能守恒。
这类题目的典型特点是系统不受摩擦力作用。
(2017·福建八县一中联考)(多选)如图所示,倾角为30°、高为L的固定斜面底端与水平面平滑相连,质量分别为3m、m的两个小球A、B用一根长为L的轻绳连接,A球置于斜面顶端。
现由静止释放A、B两球,B球与弧形挡板碰撞过程时间极短,无机械能损失,且碰后只能沿斜面下滑,两球最终均滑到水平面上。
已知重力加速度为g,不计一切摩擦,则(ABD)A.A球刚滑至水平面上时的速度大小为5gL2B.B球刚滑至水平面上时的速度大小为32gLC.两小球在水平面上不可能相撞D.在A球沿斜面下滑的过程中,轻绳对B球先做正功,后不做功[解析]从A球开始下滑到A球落地的过程中,系统的机械能守恒,A球到达水平面上时B球在斜面的中点上,则有3mgL-mg L2=12(4m)v2,解得v=5gL2,故A正确;A球滑到水平面后,A球的速度不再变化,而B球速度继续增大,此时轻绳对B球不再有力的作用,对B球由机械能守恒可知mg 12L=12mv′2-12mv2,解得B球最终滑到水平面上时速度v′=32gL,故B正确;B球滑到水平面上,由于B球的速度大于A球的速度,故两球最终一定会相撞,故C错误;由题意可知,开始时,B球动能增加,轻绳对B球做正功,当A球沿斜面下滑一半距离后,A、B球一起沿斜面下滑,速度和加速度均相等,故轻绳无拉力,轻绳不再做功,故D正确。
一、机械能守恒定律在连接体问题中的应用机械能守恒定律的研究对象是几个相互作用的物体组成的系统时,在应用机械能守恒定律解决系统的运动状态的变化及能量的变化时,经常出现下面三种情况:1.系统内两个物体直接接触或通过弹簧连接。
这类连接体问题应注意各物体间不同能量形式的转化关系。
2.系统内两个物体通过轻绳连接。
如果和外界不存在摩擦力做功等问题时,只有机械能在两物体之间相互转移,两物体组成的系统机械能守恒。
解决此类问题的关键是在绳的方向上两物体速度大小相等。
3.系统内两个物体通过轻杆连接。
轻杆连接的两物体绕固定转轴转动时,两物体的角速度相等。
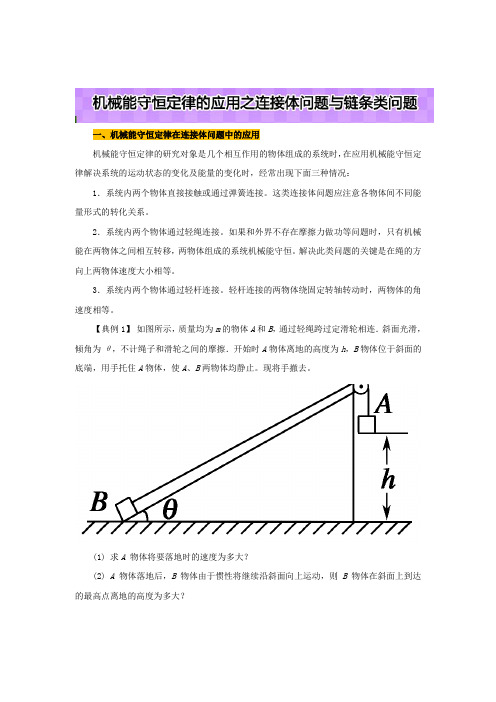
【典例1】如图所示,质量均为m的物体A和B,通过轻绳跨过定滑轮相连.斜面光滑,倾角为θ,不计绳子和滑轮之间的摩擦.开始时A物体离地的高度为h,B物体位于斜面的底端,用手托住A物体,使A、B两物体均静止。
现将手撤去。
(1) 求A 物体将要落地时的速度为多大?(2) A 物体落地后,B 物体由于惯性将继续沿斜面向上运动,则B 物体在斜面上到达的最高点离地的高度为多大?(2)A 物体落地后,B 物体由于惯性将继续沿斜面向上运动,此时绳子对其没有拉力,对B 物体而言,只有重力做功,故机械能守恒,设其到达的最高点离地高度为H ,由机械能守恒定律得12mv 2= mg (H -h sin θ) 解得H =h+sin θ2.【答案】 (1)gh-sin θ(2)h+sin θ2【典例2】 如图所示,质量分别为2m 和m 的可视为质点的小球A 、B ,用质量不计且不可伸长的细线相连,跨在固定的底面半径为R 的光滑圆柱体两侧。
开始时A 球和B 球均与圆柱体轴心O 等高,然后释放两球,则B 球到达圆柱体最高点时的速度为多大?【审题指导】解答本题时应注意以下两点:(1)运动过程中,A 球和 B 球均受到细线的拉力作用,细线的拉力做功,A 球和B 球的机械能都不守恒。
(2)若选取A 球和B 球及细线组成的系统为研究对象,则运动过程中只有重力做功,系统的机械能守恒。
机械能守恒中的连接体问题【解题步骤】1.准确选择研究对象2.判定机械能是否守恒3.应用机械能守恒处理连接体问题例1:如图,在光滑的水平桌面上有一质量为M的小车,小车与绳的一端相连,绳子的另一端通过光滑滑轮与一个质量为m 的砝码相连,砝码到地面的高度为h,由静止释放砝码,则当其着地前的一瞬间(小车未离开桌子)小车的速度为多大?练习Word文档1、一根细绳绕过光滑的定滑轮,两端分别系住质量为M和m的长方形物块,且M>m,开始时用手握住M,使系统处于如图示状态。
求Array(1)当M由静止释放下落h高时的速度(2)如果M下降h刚好触地,那么m上升的总高度是多少?2、如图所示,一固定的三角形木块,其斜面的倾角θ=30°,另一边与地面垂直,顶上有一定滑轮。
一柔软的细线跨过定滑轮,两端分别与物块A和B连接,A的质量为4m,B的质量为m。
开始时将B按在地面上不动,然后放开手,让A沿斜面下滑而B上升。
物块A与斜面间无摩擦。
设当A沿斜面下滑S距离后,细线突然断了。
Word文档求物块B上升的最大高度H。
3、如图光滑圆柱被固定在水平平台上,质量为m1的小球甲用轻绳跨过圆柱与质量为m2的小球乙相连,开始时让小球甲放在平台上,两边绳竖直,两球均从静止开始运动,求当甲上升到圆柱最高点时甲的速度。
Word文档例2.长为L质量分布均匀的绳子,对称地悬挂在轻小的定滑轮上,如图所示.轻轻地推动一下,让绳子滑下,那么当绳子离开滑轮的瞬间,求绳子的速度?练习Word文档1、如图所示,一粗细均匀的U形管装有同种液体竖直放置,右管口用盖板A密闭一部分气体,左管口开口,两液面高度差为h,U形管中液柱总长为4h,现拿去盖板,液柱开始流动,当两侧液面恰好相齐时,右侧液面下降的速度大小为多少?Ah2.如图所示,把小车放在光滑的水平桌面上,用轻绳跨过定滑轮使之与盛有沙子的小桶相连,已知小车的质量为M,小桶与沙子的总质量为m,把小车从静止状态释放后,在小桶下落竖直高度为h的过程中,若不计滑轮及空气的阻力,下列说法中正确的是A.绳拉车的力始终为mgB.当M远远大于m时,才可以认为绳拉车的力为mgC.小车获得的动能为mghD.小车获得的动能为Word文档Word 文档例题3.如图所示,质量分别为2m 和3m 的两个小球固定在一根直角尺的两端A 、B ,直角尺的顶点O 处有光滑的固定转动轴.AO 、BO 的长分别为2L 和L .开始时直角尺的AO 部分处于水平位置而B 在O 的正下方.让该系统由静止开始自由转动,求:当A 到达最低点时,A 小球的速度大小v ;匀速圆周运动一、物理量之间的转换例1、如图所示的皮带传动装置中,右边两轮是连在一起同轴转动,图中三轮半径的关系为:,,A 、B 、C 三点为三个轮边缘上的点,皮带不打滑,则A 、B 、C 三点的线速度之比为__________,角速度之比为__________,周期之比为__________。
9 专题:动能定理和机械能守恒定律综合应用连接体和链条问题[学习目标]1.知道动能定理与机械能守恒定律的区别,体会二者在解题时的方法异同2.能灵活运用动能定理和机械能守恒定律解决综合题目.3.会分析多个物体组成系统的机械能守恒问题.4.会分析处理链条类机械能守恒问题一、机械能的变化量ΔE与其他力做功的关系质量为m的物块在竖直向上的恒力F的作用下由静止向上加速运动了h,此过程恒力F做功多少,物块机械能变化了多少?(空气阻力不计,重力加速度为g)二、多物体组成的系统机械能守恒问题1.当动能、势能仅在系统内相互转化或转移,则系统的机械能守恒.2.机械能守恒定律表达式的选取技巧①当研究对象为单个物体时,可优先考虑应用表达式E k1+E p1=E k2+E p2或ΔE k=-ΔE p来求解.②当研究对象为两个物体组成的系统时:a.若两个物体的重力势能都在减小(或增加),动能都在增加(或减小),可优先考虑应用表达式ΔE k=-ΔE p来求解.b.若A物体的机械能增加,B物体的机械能减少,可优先考虑用表达式ΔE A=-ΔE B来求解.c.从机械能的转化角度来看,系统中一个物体某一类型机械能的减少量等于系统中其他类型机械能的增加量,可用ΔE减=ΔE增来列式.d.注意寻找连接各物体间的速度关系的连接物,如绳子、杆或者其他物体,然后在寻找几个物体间的速度关系和位移关系。
3.对于关联物体的机械能守恒问题,应注意寻找用绳或杆相连接的物体间的速度关系、位移与高度变化量Δh 的关系.三、连接体问题解题思路与技巧1.不含弹簧的系统机械能守恒问题①对多个物体组成的系统,要注意判断物体运动过程中系统的机械能是否守恒.一般情况为:不计空气阻力和一切摩擦,系统的机械能守恒.②注意寻找用绳或杆相连接的物体间的速度关系和位移关系.③多个物体组成的系统,应用机械能守恒时,先确定系统中哪些能量增加、哪些能量减少,再用ΔE增=ΔE减(系统内一部分增加的机械能和另一部分减少的机械能相等)解决问题.2.含弹簧的系统机械能守恒问题①通过其他能量求弹性势能,根据机械能守恒,列出方程,代入其他能量的数值求解.②对同一弹簧,弹性势能的大小由弹簧的形变量决定,弹簧伸长量和压缩量相等时,弹簧弹性势能相等.③物体运动的位移与弹簧的形变量或形变量的变化量有关.知识点一:动能定理和机械能守恒定律的比较动能定理和机械能守恒定律,都可以用来求能量或速度,但侧重不同,动能定理解决物体运动,尤其计算对该物体的做功时较简单,机械能守恒定律解决系统问题往往较简单,两者的灵活选择可以简化运算过程.【探究重点】【例题精讲】1.(2022届·河北省唐山市高三上学期期末)如图所示,一劲度系数为k的轻弹簧左端固定在竖直墙壁上,右端连接置于粗糙水平面的物块。
知识回顾1.机械能守恒的判定(1)若物体只有重力和弹簧弹力做功,则物体和弹簧组成的系统机械能守恒.(2)若系统只有动能和势能的相互转化,没有机械能与其他形式的能的相互转化,如摩擦热等,则系统机械能守恒.2.机械能守恒的形式规律方法一物体或多物体参与多个运动过程的求解方法(1)若一个物体或多个物体参与了多个运动过程,有的过程只涉及运动和力的问题或只要求分析物体的动力学特点,则要用动力学方法求解.(2)若某过程涉及做功和能量转化问题,则要考虑应用动能定理、机械能守恒定律或功能关系求解.例题分析【例1】 (2017年安徽六校联考)一质量不计的直角形支架两端分别连接质量为m 和2m 的小球A 和B .支架的两直角边长度分别为2l 和l ,支架可绕固定轴O 在竖直平面内无摩擦转动,如图所示.开始时OA 边处于水平位置,由静止释放,则( )A .A 球的最大速度为2B .A 球速度最大时,B 球的重力势能最小C .A 球速度最大时,两直角边与竖直方向的夹角为45°D .A 、B 两球最大速度之比v A ∶v B =1∶2【答案】 C【例2】 (2017年重庆调研)如图所示,A 、B 、C 三个可视为质点的物体通过轻绳连接,A 、B 间轻绳长为L .C 静置于水平地面上,用手托住A ,两段轻绳都伸直,A 距水平地面高也为L ,然后将A 从静止开始释放.已知物体A 、B 的质量均为m ,物体C 的质量为23m ,重力加速度为g ,定滑轮光滑且质量不计,不计空气阻力,物体A 着地后不反弹.求:(1)刚释放A 时,A 、B 间绳的弹力大小F T ;(2)运动过程中,物体C 距离地面的最大高度H .【答案】F T =76mg ; H =712L【解析】 (1)刚释放A 时,物体加速度大小为a ,将A 、B 、C 看成一个系统,由牛顿第二定律得2mg -23mg =m 3a以物体A 为研究对象.由牛顿第二定律得mg -F T =ma解得运动过程中,物体C 距离地面的最大高度为H =L +h =712L 。