江苏专版2018年高考数学三轮冲刺专题平面解析几何点对点试卷【word版】.doc

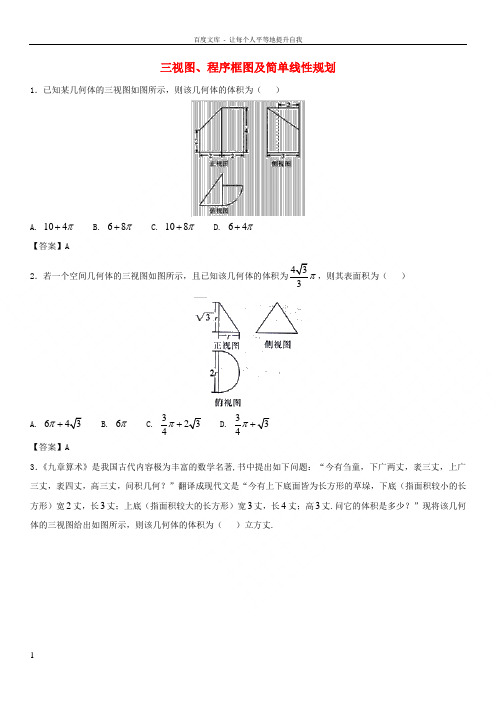
三视图、程序框图及简单线性规划1．已知某几何体的三视图如图所示，则该几何体的体积为（ ）A. 104π+B. 68π+C. 108π+D. 64π+ 【答案】A2．若一个空间几何体的三视图如图所示，且已知该几何体的体积为433π，则其表面积为（ ）A. 63π+B. 6πC. 3234π+334π+ 【答案】A3．《九章算术》是我国古代内容极为丰富的数学名著,书中提出如下问题：“今有刍童，下广两丈，袤三丈，上广三丈，袤四丈，高三丈，问积几何？”翻译成现代文是“今有上下底面皆为长方形的草垛，下底（指面积较小的长方形）宽2丈，长3丈；上底（指面积较大的长方形）宽3丈，长4丈；高3丈.问它的体积是多少？”现将该几何体的三视图给出如图所示，则该几何体的体积为（ ）立方丈.A.532B. 24C. 27D. 1862+【答案】A4．如图所示，一个三棱锥的的三视图是三个直角三角形，则该三棱锥的体积为（）A. 3B. 4C. 6D. 85．已知实数x，y满足10{10330x yx yx y-+≥+-≥--≤，则使不等式1kx y k-+≤恒成立的实数k的取值集合是（）A. (],1-∞ B.1,2⎛⎤-∞⎥⎝⎦C.1,4⎛⎤-∞⎥⎝⎦D.1,8⎛⎤-∞⎥⎝⎦【答案】B6．在由不等式组2140,{3,2,x yxy-+≥≤-≥所确定的三角形区域内随机取一点，则该点到此三角形的三个顶点的距离均不小于1的概率是( )A. 92π- B. 9π- C. 19π- D. 118π－【答案】D7．已知变量x ， y 满足2{220 240x y x y x y -≥++≥--≤，若方程2260x y y k ++-=有解，则实数k 的最小值为（ ）A.45455- B. 295- C. 4533+ D. 165【答案】B8．设,x y 满足约束条件260{20 20x y x y y -+≥-≤-≤，则x y -的取值范围为（ ）A. []0,4B. []2,4C. []0,2D. []2,6 【答案】A9．执行如图所示的程序框图，则输出的a =（ ）A. 14-B. 45C. 4D. 5 【答案】D10．执行如图所示的程序框图,如果输入的x 、t 均为3，则输出的M 等于（ ）A. 23B.113C.196D.436【答案】C11．执行如图所示的程序框图，则输出的S （）A. 17B. 33C. 65D. 129【答案】C12．《九章算术》中,将底面是直角三角形的直三棱柱称之为“堑堵”,已知某“堑堵”的三视图如图所示,则该“堑堵”的表面积为（）A. 2B. 4C.D.【答案】D13．【2017届福建省泉州市高三3月质量检测】某几何体的三视图如图所示,则该几何体的侧视图中的虚线部分是 （ ）A. 圆弧B. 抛物线的一部分C. 椭圆的一部分D. 双曲线的一部分 【答案】D14．如图,网格纸上小正方形的边长为1,粗实线画出的是某几何体的三视图,若该几何体的顶点都在球O 的球面上,则球O 的表面积为（ ）A.B.C.D.【答案】A15．若()21log 12,31x y x ≤-+≤-≤,则2x y -的最大值与最小值之和是（ ） A. 0 B. -2 C. 2 D. 6 【答案】C16．若变量,x y 满足约束条件{11y xx y y ≤+≤≥-,且2z x y =+的最大值和最小值分别为m 和n ,则m n +=（ ）A. -2B. -1C. 0D. 1【答案】C17．不等式组20{10220xyx y-≤-≤+-≥表示的平面区域的面积是（）A. 1B. 2C. 3D. 4【答案】A18．当4n=时,执行如图所示的程序框图,输出的S值为（）A. 6B. 8C. 14D. 30【答案】D19．一种在实数域和复数域上近似求解方程的方法可以设计如图所示的程序框图,若输入的,则输出的结果（）A. 4B.1C.D.【答案】C20．右边程序框图的算法思路源于数学名著《几何原本》中的“辗转相除法”,执行该程序框图（图中“m MOD n”表示除以的余数）,若输入的,分别为485,135,则输出的=（）A. 0B. 5C. 25D. 45【答案】B21. 如图在棱长为1的正方体网格中,粗线画出的是某几何体的三视图,则该几何体的体积为 ( ).A．117 B.111 C．99 D. 75【答案】D22. 某几何体的三视图如图所示,则该几何体的体积为（）A．5B．4C．2D．1【答案】A．23．已知不等式组202020x yyx y-+≥⎧⎪+≥⎨⎪++≤⎩表示的平面区域,则231x yzx+-=-的最大值 .【答案】()()22224x y+++=24.已知不等式组⎪⎩⎪⎨⎧≥-≥-≤+11yyxyx所表示的平面区域为D,若直线3y kx=-与平面区域D有公共点,则k的取值范围为是A．[3,3]- B．11(,][,)33-∞-+∞ C．(,3][3,)-∞-+∞ D．11[,]33-【答案】C正视图侧视图。

全国著名重点中学领航高考冲刺试卷数 学(江苏卷)12命题：王建宏本试卷分为第I 卷（填空题）、第II 卷（解答题）和第Ⅲ卷（附加题）三部分，文科考生只要求．．．做第I 卷、第II 卷，第Ⅲ卷．．．不做．．，满分160分，考试时间120分钟；理科考生第I 卷、第II 卷和第Ⅲ卷都必须做．．．．，满分160+40分，考试时间120＋30分钟。

第I 卷（填空题 共70分）一、填空题：本大题共14小题，每小题5分，共70分. 1．不等式0.5log x ≥－1 的解集是 ▲ ．2．执行下列伪代码的结果是 ▲ ． A ←4.5 B ←6If A ≥5 Then B ←B ＋1 ElseB ←B －3 B ←B ＋2 End IfIf B ≥4 Then B ←B ×BElseB ←A ＋BEnd IfPrint B3．二次函数的图像经过点(1,2)，且在[1,)-+∞上是增函数，则该二次函数的解析式可以是 ▲ ．4．已知x ∈R ，下列函数：①x x y 1+=；②2y =；③2322++=x x y ；④2y x x ．这些函数中最小值为2的函数是 ▲ （注：把你认为正确的序号都填上）．5．若复数iia 213++（a ∈R ，i 为虚数单位）是纯虚数，则实数a ＝ ▲ ．6．已知e 1，e 2是两个单位向量，它们的夹角为60o ，则(2 e 1－e 2)⋅(－3 e 1＋2 e 2)＝ ▲ ．7．等差数列中前n 项和为210，其中前4项和为40，后4项和为80，则n ＝ ▲ ．8．已知圆O 1：22()()4x a y b -+-=，圆O 2：22(1)(2)1x a y b --+--=，其中a ，b ∈R ，那么，两圆的位置关系是 ▲ ． 9．将函数sin 2y x =的图像向左平移8π平移后,得到的函数图像所对应的解析式为 ▲ ．10．右图是一个空间几何体的三视图，各户图中的尺寸（单位：cm ），则该几何体的表面积是 ▲ cm 2．11．已知点A (2,4)，B (1,1)，C (4,2)，若以ΔABC （包含边界）为可行域，要使目标函数(0)z ax y a =+>取得最大值的最优解有无穷多个，则a ＝ ▲ ．12．已知命题p ：,(0,)a b ∃∈+∞，当1a b +=时，113a b+=；命题q ：x ∀∈R ，21x x -+≥0恒成立．则命题p ⌝且q 是 ▲ 命题（填“真”或“假”）．13．函数f （x ）的定义域为开区间（a ，b ），导函数'()f x 在（a ，b ）内的图像如图所示，则函数f （x ）在开区间（a ，b ）内极小值点有▲ 个．14．已知命题：平面直角坐标系xOy 中，已知ABC ∆顶点(,0)A p -和(,0)C p ，顶点B 在椭圆22221x y m n+=（m ＞n ＞0，p ）上，椭圆的离心率是e ，则sin sin sin A C B+=1e ．试将该命题类比到双曲线中，给出一个真命题： ▲ ▲ ．第Ⅱ卷（解答题 共90分）二、解答题：本大题共6小题，共90分.解答应写出文字说明、证明过程或演算步骤.15.（本小题满分14分）已知向量m (cos ,sin )αα=，n ＝(cos ,sin )ββ，02πα<<，02πβ-<<，|m －n|=，求s i n ()αβ-．33 2主视图俯视图左视图16.（本小题满分14分）如图，四棱锥P-ABCD 中，底面ABCD 是矩形，P A ⊥底面ABCD ，P A ＝AB ＝1，AD ＝ 3 ，点F 是PB 的中点，点E 在BC 上移动．（1）求三棱锥E-P AD 体积；（2）当点E 为BC 的中点时，试判断EF 与平面P AC 的关系，并说明理由；（3）证明：无论点E 在边BC 的何处，都有PE ⊥AF ．17.（本小题满分14分）已知圆C ：2230x y Dx Ey ++++=，圆C 关于直线10x y +-=对称，圆心在第二象限，半径为2． （1）求圆C 的方程；（2）已知不过原点的直线l 与圆C 相切，且在x 轴、y 轴上的截距相等，求直线l 方程。

全国著名重点中学领航高考冲刺试卷数 学(江苏卷)13命题：王建宏本试卷分为第I 卷（填空题）、第II 卷（解答题）和第Ⅲ卷（附加题）三部分，文科考生只要求．．．做第I 卷、第II 卷，第Ⅲ卷．．．不做．．，满分160分，考试时间120分钟；理科考生第I 卷、第II 卷和第Ⅲ卷都必须．．．做．，满分160+40分，考试时间120＋30分钟. 第I 卷（填空题 共70分）一、填空题：本大题共14小题，每小题5分，共70分.1．函数y =的定义域是 ▲ ．2．已知全集是实数集R ，{|20},{|1},A x x B x x =-≤≤=<则（R A ð）B = ▲ ． 3．要得到sin(2)4y x π=+的图像，只需将函数sin 2y x =的图像向 ▲ （左，右）平移 ▲ 个单位得到。

4．复数21(1)i-的共轭复数是 ▲ ．5．关于直线l n m ,,及平面N M ,，下列命题中正确的命题为 ▲ ．⑴ 若M n M m //,//，则n m //， ⑵ n m M m ⊥,//，则M n ⊥，⑶ 若M n M m ⊂⊂,，且n l m l ⊥⊥,，则M l ⊥ ⑷ 若N m M m //,⊥，则N M ⊥6．自圆222440x y x y +--+=外一点(0,4)P 向圆引两条切线，切点分别为,A B ，则PA PB ⋅ 等于 ▲ ．7．过抛物线22(0)y px p =>的焦点F作直线交抛物线于两点,A B ，O 为原点，则ABO ∆的形状为 ▲ ．8．数列{}n a 满足112,21n n a a a +==+，若数列{}n a c +恰为等比数列，则常数c 的值是 ▲ ．9．已知{}{}),(,)2()1(,3,)1()3(,2R b a i b a i N i b a M ∈++-=-++=.若φ≠N M ,则=+b a ▲ ．10．下面的程序运行时输出的结果是 ▲ ．1←i 0←S While 5<i1+←i ii i S S *+←End While int Pr S End11． 若函数2()min{2,log },f x x x =-+ 其中min{,}p q 表示,p q 两者中的较小者，则不等式()1f x <-的解集为 ▲ ．12．已知球O 是棱长为12的正四面体ABC S -的外接球,F E D ,,分别是棱SC SB SA ,,的中点,则平面DEF 截球O 所得截面的面积是 ▲ ．13．对正整数n ,设抛物线x n y )12(22+=,过)0,2(n P 任作直线l 交抛物线于n A ,n B 两点,则数列⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧+⋅)1(2n OB OA n n 的前n 项和为 ▲ ．14．符号][x 表示不超过x 的最大整数,如2]88.1[,2][-=-=e ,定义函数{}][x x x -=,那么下列命题中正确的序号是 ▲ ． (1)函数{}x 的定义域为R ,值域为)1,0[; (2)方程{}21=x ,有无数解;(3)函数{}x 是周期函数; (4)函数{}x 是增函数.第Ⅱ卷（解答题 共90分）二、解答题：本大题共6小题，共90分.解答应写出文字说明、证明过程或演算步骤.15.（本小题满分14分.第1小题6分，第2小题8分）从10位同学(其中6女,4男)中随机选3位参加测验,每位女同学能通过测验的概率均为54,每位男同学能通过测验的概率均为53,试求: ⑴ 选出的3位同学中,至少有一位男同学的概率;⑵ 10位同学中的女同学甲和男同学乙同时被选中且通过测验的概率.16.（本小题满分14分.第1小题6分，第2小题8分） 已知三点),0(),sin ,(cos ),3,0(),0,3(πααα∈C B A ,若52=⋅,求：⑴ ααcos sin +的值； ⑵ 2sin )6sin(2απα++的值.17.（本小题满分14分,第一小题4分,第二小题5分,第三小题5分）在式子n +⋅⋅⋅+++321中,划去最前面的“1”后,在式子后面添上“1-”;再划去前面的“2+”, 在式子后面添上“2-”;如此循环下去.(即每划去前面一个数(连同符号)后,就在式子后面添上这个数的相反数)⑴ 当100=n 时,后面添上第m 个数)(n m <时所得式子的值是2500,求m 的值.⑵ 当后面添上第3-n 个数时所得式子的值最大,求这个最大值并求此时n 的值; ⑶ 当2008=n时,所得式子有无最小值?若有,求出这个值,并指出是后面添了多少个数时所得式子的值;若没有,请说明理由.18.（本小题满分16分，第1小题4分，第2小题6分，第3小题6分）已知椭圆方程222213x y b b +=，（0b >），经过椭圆右焦点且斜率为1的直线l 交椭圆于A ，B 两点，设点M 为椭圆上任一点，且OM OA OB λμ=+⑴ 试写出直线l 的方程； ⑵ 计算AB 的长度； ⑶ 证明221λμ+=.19．（本小题满分16分，第（1）、（2）小问各4分，第（3）小问8分）已知函数ay x x =+有如下性质：如果常数0a >，那么该函数在上是减函数，在)+∞是增函数. ⑴ 如果函数2by x x =+（0x >）的值域为[6,)+∞，求b 的值；⑵ 研究函数22C y x x =+（常数0C >）在(0,)+∞上的单调性，并说明理由；⑶ 对函数a y x x =+和22a y x x=+（常数0a >）作出推广，使它们都是你所推广的函数的特例.研究推广后的函数的单调性（只需写出结论，不必证明），并求函数2211()()()n nF x x x x x =+++（n 是正整数）在区间1[,2]2上的最大值和最小值（可利用你的研究结论）.20．（本小题满分16分，第（1）、（2）小问各4分，第（3）小问8分） 已知函数3()3()f x x ax a R =-∈.⑴ 当1a =时，求()f x 的极小值；⑵ 若直线0x y m ++=对任意的m R ∈都不是曲线()y f x =的切线，求a 的取值范围； ⑶ 设()|()|,[1,1]g x f x x =∈-，求()g x 的最大值()F a 的解析式.第Ⅲ卷（附加题 共40分）本大题6小题，共40分，其中第一、第二小题每小题12分为必做题；第三、第四、第五、第六小题中选做两小题，多做无效，每小题8分。

解析几何 1.已知点F 为双曲线C ： 22221(0)x y a b a b-=>>的右焦点，点P 是双曲线右支上的一点， O 为坐标原点，若2FP OF =， 120OFP ∠=，则双曲线C 的离心率为（ ）31-31+31-31+ 2. 双曲线2222:1(0,0)x y C a b a b-=>>的右焦点和虚轴上的一个端点分别为,F A ，点P 为双曲线C 左支上一点，若APF ∆周长的最小值为6b ，则双曲线C 的离心率为（ ）56858510 3.已知抛物线2:4C y x =的焦点为F ，准线为l ，过点F 的直线交抛物线于,A B 两点（A 在第一象限），过点A 作准线l 的垂线，垂足为E ，若60AFE ∠=︒，则AFE ∆的面积为（ ） A. 432343234.已知椭圆1C 和双曲线2C 焦点相同，且离心率互为倒数， 12,F F 是它们的公共焦点， P 是椭圆和双曲线在第一象限的交点，若1260F PF ∠=︒，则椭圆1C 的离心率为（ ）332 D. 125．已知圆M 与直线340x y -=及34100x y -+=都相切，圆心在直线4y x =--上，则圆M 的方程为（ ）A. ()()22311x y ++-=B. ()()22311x y -++=C. ()()22311x y +++=D. ()()22311x y -+-=6．已知双曲线的离心率为，其一条渐近线被圆截得的线段长为，则实数m 的值为（ ）A. 3B. 1C.D. 27.设直线l ： 3x 4y 40++=，圆C ： ()222x 2y r (r 0)-+=>，若圆C 上存在两点P ， Q ，直线l 上存在一点M ，使得PMQ 90∠=︒，则r 的取值范围是_____.8．已知直线12:0,:20l mx y l x my m -=+--=.当m 在实数范围内变化时， 1l 与2l 的交点P 恒在一个定圆上，则定圆方程是 ______ .9.已知抛物线2:6C y x =的焦点为F ，过点F 的直线l 交抛物线于两点,A B ，交抛物线的准线于点C ，若3FC FA =，则FB =__________．10.已知椭圆2222:1(0)x y E a b a b +=>>经过点53,22⎛⎫ ⎪ ⎪,离心率为255，点O 坐标原点.（1）求椭圆E 的标准方程；（2）过椭圆E 的左焦点F 任作一条不垂直于坐标轴的直线l ，交椭圆E 于,P Q 两点，记弦PQ 的中点为M ，过F 作PQ 的垂线FN 交直线OM 于点N ，证明：点N 在一条定直线上.11.已知椭圆W ：x 2a 2＋y 2b2＝1(a >b >0)的焦距为2，过右焦点和短轴一个端点的直线的斜率为－1，O 为坐标原点. (1)求椭圆W 的方程；(2)设斜率为k 的直线l 与W 相交于A ，B 两点，记△AOB 面积的最大值为S k ，证明：S 1＝S 2.12.已知动圆C 恒过点1,02⎛⎫ ⎪⎝⎭，且与直线12x =-相切. （1）求圆心C 的轨迹方程；（2）若过点()3,0P 的直线交轨迹C 于A ， B 两点，直线OA ， OB （O 为坐标原点）分别交直线3x =-于点M ，N ，证明：以MN 为直径的圆被x 轴截得的弦长为定值.13.已知椭圆C ： 22221x y a b +=（0a b >> ）的左右焦点分别为1F ， 2F ，离心率为12，点A 在椭圆C 上， 12AF =， 1260F AF ∠=︒，过2F 与坐标轴不垂直的直线l 与椭圆C 交于P ， Q 两点．（Ⅰ）求椭圆C 的方程； （Ⅱ）若P ， Q 的中点为N ，在线段2OF 上是否存在点(),0M m ，使得MN PQ ⊥？若存在，求实数m 的取值范围；若不存在，说明理由．14．已知椭圆C ： 22221(0)x y a b a b +=>>的长轴长为4，且经过点31,2⎛⎫⎪⎝⎭.（1）求椭圆C 的标准方程；（2）过椭圆右焦点F 作两条互相垂直的弦AB 与CD ，求AB CD +的取值范围.。

绝密★启封前2018江苏省高考压轴卷数 学I注意事项考生在答题前请认真阅读本注意事项及各题答题要求1.本试卷共4页，包含非选择题（第1题 ~第20题，共20题）.本卷满分为160分，考试时间为120分钟。

考试结束后，请将本试卷和答题卡一并交回。

2.答题前，请务必将自己的姓名、准考证号用0.5毫米黑色墨水的签字笔填写在试卷及答题卡的规定位置。

3.请认真核对监考员在答题上所粘贴的条形码上的姓名、准考证号与本人是否相符。

4.作答试题，必须用0.5毫米黑色墨水的签字笔在答题卡上的指定位置作答，在其他位置作答一律无效。

5.如需改动，须用2B 铅笔绘、写清楚，线条、符号等须加黑、加粗一、填空题：本大题共14小题，每小题5分，共计70分，请把答案填写在答题卡相应位置上 1.若集合A={﹣1，0，1，2}，B={x|x+1＞0}，则A∩B= ．2.若复数z 满足z （1﹣i ）=2i （i 是虚数单位），z 是z 的共轭复数，则z = ．3.某学校对高二年级期中考试数学成绩进行分析，随机抽取了分数在[100，150]的1000名学生的成绩，并根据这1000名学生的成绩画出频率分布直方图（如图所示），则成绩在[120，130）内的学生共有 人．4.如图，该程序运行后输出的结果为 ．5.将函数y=3sin （2x ﹣6π）的图象向左平移4π个单位后，所在图象对应的函数解析式为 ． 6.如图，在长方体ABCD ﹣A 1B 1C 1D 1中，AB=AD=3cm ，AA 1=2cm ，则三棱锥A ﹣B 1D 1D 的体积为 cm 3．7.如图，在一个面积为8的矩形中随机撒一粒黄豆，若黄豆落到阴影部分的概率为41，则阴影部分的面积为 ．8.已知双曲线﹣=1（a ＞0，b ＞0）的左、右端点分别为A 、B 两点，点C （0， b ），若线段AC的垂直平分线过点B ，则双曲线的离心率为 ． 9.设公比不为1的等比数列{a n }满足a 1a 2a 3=﹣81，且a 2，a 4，a 3成等差数列，则数列{a n }的前4项和为 ． 10.设定义在R 上的偶函数f （x ）在区间（﹣∞，0]上单调递减，若f （1﹣m ）＜f （m ），则实数m 的取值范围是 ．11.已知函数f （x ）=，若a 、b 、c 互不相等，且f （a ）=f （b ）=f （c ），则a+b+c 的取值范围是 ．12.如图，在△ABC 中，已知=21，P 是BN 上一点，若AP =m AB +41，则实数m 的值是 ．13.已知非零向量a ，b 满足|a |=|b |=|a +b |，则a 与2a －b 夹角的余弦值为 ．14.已知函数f(x)=⎩⎨⎧≥++-<1x ,a x 25x 9x 1x ,x sin 23，若函数f （x ）的图象与直线y=x 有三个不同的公共点，则实数a 的取值集合为 ． 15.如图，在三棱柱1B 1C 1中，，点E ，F 分别在棱BB 1 ，CC 1上（均异于端点），且∠∠ACF ，AE ⊥BB 1，AF ⊥CC 1．求证：（1）平面AEF ⊥平面BB 1C 1C ； （2）BC // 平面AEF ．16.在△ABC 中，角,,A B C 的对边分别为,,a b c ，且()2cos cos a b C c B -⋅=⋅. （1）求角C 的大小；（2）若2c =，△ABC 3.17.已知中心在坐标原点的椭圆C ，F 1，F 2 分别为椭圆的左、右焦点，长轴长为6，离心率为（1）求椭圆C 的标准方程；（2）已知点P 在椭圆C 上，且PF 1=4，求点P 到右准线的距离．18.如图，四棱锥P ﹣ABCD 中，PA ⊥平面ABCD ，四边形ABCD 为直角梯形，AD ∥BC ，∠BAD=∠CBA=90°，PA=AB=BC=1，AD=2，E ，F ，G 分别为BC ，PD ，PC 的中点． （1）求EF 与DG 所成角的余弦值；（2）若M 为EF 上一点，N 为DG 上一点，是否存在MN ，使得MN ⊥平面PBC ？若存在，求出点M ，N 的坐标；若不存在，请说明理由．19.设等比数列a 1，a 2，a 3，a 4的公比为q ，等差数列b 1，b 2，b 3，b 4的公差为d ，且10q d ≠≠，． 记i i i c a b =+（，2，3，4）．（1）求证：数列123c c c ，，不是等差数列； （2）设11a =，2q =．若数列123c c c ，，是等比数列，求b 2关于d 的函数关系式及其定义域； （3）数列1234c c c c ，，，能否为等比数列？并说明理由． 20.（16分）已知f （x ）=x 2+mx+1（m ∈R ），g （x ）=e x ．（1）当x ∈[0，2]时，F （x ）=f （x ）﹣g （x ）为增函数，求实数m 的取值范围； （2）若m ∈（﹣1，0），设函数 G(x)=)x (g )x (f ，H(x)=﹣41x+45，求证：对任意x 1，x 2∈[1，1﹣m]，G （x 1）＜H （x 2）恒成立．AA 11C 1B C FE（第16题）数学II （附加题）注意事项考生在答题前请认真阅读本注意事项及各题答题要求1.本试卷共2页，均为非选择题（第21题 ~第23题）。

平面解析几何1．在平面直角坐标系中，曲线上任意一点P 到直线的距离的最小值为__________． 【答案】2．在平面直角坐标系中，若圆 上存在点P ，且点P 关于直线的对称点Q 在圆上，则r 的取值范围是____． 【答案】3．在平面直角坐标系xOy 中，已知点F 为抛物线28y x =的焦点，则点F 到双曲线221169x y -=的渐近线的距离为________. 【答案】654．在平面直角坐标系xOy 中，已知点()4,0A -， ()0,4B ，从直线AB 上一点P 向圆224x y +=引两条切线PC ，PD ，切点分别为C ， D .设线段CD 的中点为M ，则线段AM 长的最大值为_________.【答案】5．在平面直角坐标系xOy 中，双曲线22:1(0)4x y C m m-=>的一条渐近线与直线210x y +-=垂直，则实数m 的值为__________．【答案】166．已知圆22:5,,O x y A B +=为圆O 上的两个动点，且2,AB M =为弦AB 的中点， ()(),2C a D a +.当,A B 在圆O 上运动时，始终有CMD ∠为锐角，则实数a 的取值范围为__________．【答案】()(),20,-∞-⋃+∞7．在平面直角坐标系xOy 中，已知圆()(22:11C x y -+-=和两点()(),2,,2A a a B a a ---，且1a >，若圆C 上存在两个不同的点,P Q ，使得90APB AQB ∠=∠=︒，则实数a 的取值范围为__________．【答案】11a ≤≤+8．经过点()20，且圆心是直线2x =与直线4x y +=的交点的圆的标准方程为________． 【答案】()()22224x y -+-=9．在平面直角坐标系中，若直线l 与圆221:1C x y +=和圆((222:49C x y -+-=都相切，且两个圆的圆心均在直线l 的下方，则直线l 的斜率为__________．【答案】710．在平面直角坐标系xOy 中，直线l 1：kx －y ＋2＝0与直线l 2：x ＋ky －2＝0相交于点P ，则当实数k 变化时，点P 到直线x －y －4＝0的距离的最大值为________．【答案】311．在平面直角坐标系xOy 中，抛物线y 2＝6x 的焦点为F ，准线为l ，P 为抛物线上一点，PA ⊥l ，A 为垂足．若直线AF 的斜率k ＝－，则线段PF 的长为________． 【答案】612．在平面直角坐标系中,已知过点的直线l 与圆相切,且与直线垂直,则实数__________． 【答案】1/213在平面直角坐标系中,双曲线的离心率为__________． 【答案】 14．【2016-2017学年苏锡常镇四市高三教学情况调研（一）】在平面直角坐标系中，过点的直线l 与圆交于两点，其中A 点在第一象限，且，则直线l 的方程为______________． 【答案】 15．在平面直角坐标系中，已知抛物线的焦点恰好是双曲线的右焦点，则双曲线的离心率为______________．【答案】2 16．设m R ∈，过定点A 的动直线0x my +=和过定点B 的动直线30mx y m --+=交于点(),P x y ，则PA PB +的最大值是 ．【答案】【解析】17．已知抛物线22y px =的准线方程为1x =-，焦点为,,,F A B C 为抛物线上不同的三点，,,FA FB FC 成等差数列，且点B 在x 轴下方，若0FA FB FC ++=，则直线AC 的方程为 ．【答案】012=--y x18．已知双曲线22:x 13y C -=的右焦点为,F P 是双曲线C 的左支上一点，()0,2M ，则PFM ∆周长最小值为____________．【答案】2+ 19．直线与双曲线的左支、右支分别交于两点，A 为右顶点，O 为坐标原点，若，则该双曲线的离心率为__________．【答案】20．在平面直角坐标系xOy 中，若双曲线2221(0)y x b b-=>的焦点到其渐近线的距离等于抛物线22y px =上的点(1,2)M 到其焦点的距离，则实数b = _ 【答案】221．已知O 为原点，双曲线上有一点P ，过P 作两条渐近线的平行线，且与两渐近线的交点分别为，平行四边形的面积为1，则双曲线的离心率为__________． 【答案】22．抛物线上一点到抛物线准线的距离为，点A 关于y 轴的对称点为B ，O 为坐标原点，的内切圆与切于点E ，点F 为内切圆上任意一点，则的取值范围为__________． 【答案】23.已知椭圆22221(0)x y a b a b+=>>，点12,,,A B B F 依次为其左顶点、下顶点、上顶点和右焦点，若直线 2AB 与直线 1B F 的交点恰在椭圆的右准线上，则椭圆的离心率为______.【答案】1224．已知双曲线2241ax y -=a 的值为 ．【答案】825. 在平面直角坐标系xOy 中，若圆22(1)4x y +-=上存在A ，B 两点关于点(1,2)P 成中心对称，则直线AB 的方程为 .【答案】30x y +-=26．已知方程2x +θtan x －θsin 1=0有两个不等实根a 和b ，那么过点),(),,(22b b B a a A 的直线与圆122=+y x 的位置关系是【答案】相切27. 在直角坐标系xOy 中，已知A （1，0），B （0，1），则满足224PA PB -=且在圆224x y +=上的点P 的个数为 ．【答案】228. 在平面直角坐标系xOy 中，若动点(,)P a b 到两直线1:l y x =和2:1l y x =-+的距离之和为，则22a b +的最大值是________.【答案】18本文档仅供文库使用。

HHH H H HH HHHH HC 全国著名重点中学领航高考冲刺试卷数 学(江苏卷)18命题：王建宏本试卷分为第I 卷（填空题）、第II 卷（解答题）和第Ⅲ卷（附加题）三部分，文科考生只要求．．．做第I 卷、第II 卷，第Ⅲ卷．．．不做．．，满分160分，考试时间120分钟；理科考生第I 卷、第II 卷和第Ⅲ卷都必须．．．做．，满分160+40分，考试时间120＋30分钟. 第I 卷（填空题 共70分）一、填空题：本大题共14小题，每小题5分，共70分.不需要写出解答过程，请把答案直接填空在答题．．卡相应位置上．．．．．．． 1. 已知集合A ＝{x ||x |≤2，x ∈R }，B ＝{x |x ≥a }且A ⊆B ，则实数a 的取值范围是 ▲ .2．如果复数()()21m i mi ++是实数，则实数m = ▲ .3.设a ≠b ，若关于x 的方程x 2－x+a=0和x 2－x+b=0的四个根可以组成首项为41的等差数列，则a+b 的值是 ▲ .4．已知y x ,的取值如下表所示：x0 1 3 4 y2.24.34.86.7从散点图分析，y 与x 线性相关，且ˆ0.95yx a =+，则a = ▲ . 5. 若191x yx y R +=∈+()，，则x y +的最小值是 ▲ . 6．一个几何体的三视图如图所示，其中，主视图中△ABC 是边长为2的正三角形，俯视图为正六边形，那么该几何体的体积为 ▲ .左视图主视图俯视图CBA7．下列是三种化合物的结构式及分子式，请按其规律，写出后一种化合物的分子式．．．是 ▲ .8．已知圆221:(1)1C x y ++=，圆2C 与圆1C 外切，且与直线3x =切于点(3,1)，则圆2C 的方程 为 ▲ .9. 已知点A （3,1）,B(0,0),C （3，0）.设∠BAC 的平分线AE 与BC 相交于E ，那么有λ= ，其中λ等于 ▲ . 10．若cos 2π2sin 4αα=-⎛⎫- ⎪⎝⎭cos sin αα+的值为 ▲ .11．读程序甲： i=1 乙：S=0S=0 For I From 1000 to 1 step 1 While i≤1000 S=S+i S=S+i End For i=i+l Print S End While End Print SEnd对甲、乙两程序和输出结果判断是 ▲ .12．若动点(,)P x y 在曲线2221(0)4x y b b+=>上变化，则22x y +的最大值为 ▲ .13．我国男足运动员转会至海外俱乐部常会成为体育媒体关注的热点新闻。

立体几何综合题（理）1.四棱柱1111ABCD A B C D -中，底面ABCD 为正方形， 1AA ⊥平面,ABCD M 为棱1DD 的中点， N 为棱AD 的中点， Q 为棱1BB 的中点.（1）证明：平面//MNQ 平面1C BD ；（2）若12AA AB =，棱11A B 上有一点P ，且()()1110,1A P A B λλ=∈，使得二面角P MN Q --的余弦值为132163，求λ的值.2．如图，在五面体ABCDPN 中，棱PA ⊥底面ABCD ， 2AB AP PN ==.底面ABCD 是菱形， 23BAD π∠=.（Ⅰ）求证： PNAB ；（Ⅱ）求二面角B DN C --的余弦值.3．如图四棱锥P ABCD -的底面ABCD 为菱形,且60ABC ∠=︒, 2AB PC ==, 2PA PB ==.（Ⅰ）求证：平面PAB ⊥平面ABCD ； （Ⅱ）二面角P AC B --的余弦值.4．如图,四棱锥P ABCD -的底面ABCD 是平行四边形,侧面PAD 是边长为2的正三角形, AB BD = 7=,3PB =.（Ⅰ）求证：平面PAD ⊥平面ABCD ；（Ⅱ）设Q 是棱PC 上的点,当PA 平面BDQ 时,求二面角A BD Q --的余弦值. 5．如图,已知菱形ABCD 与直角梯形ABEF 所在的平面互相垂直,其中BEAF , AB AF ⊥,122AB BE AF ===, 3CBA π∠=, P 为DF 的中点.（Ⅰ）求证： PE ∥平面ABCD ； （Ⅱ）求二面角D EF A －－的余弦值；（Ⅲ）设G 为线段AD 上一点, AG AD λ=, 若直线FG 与平面ABEF 39求AG 的长. 6．在四棱锥P ABCD -中,底面ABCD 为平行四边形, 3AB =, 22AD =, 45ABC ∠=︒, P 点在底面ABCD 内的射影E 在线段AB 上,且2PE =, 2BE EA =, F 为AD 的中点, M 在线段CD 上,且CM CD λ=．（Ⅰ）当23λ=时,证明：平面PFM ⊥平面PAB ； （Ⅱ）当平面PAM 与平面ABCD 所成的二面角的正弦值为255时,求四棱锥P ABCM -的体积． 7．如图,四棱锥P ABCD -底面为正方形,已知PD ⊥平面ABCD , PD AD =,点M 为线段PA 上任意一点（不含端点）,点N 在线段BD 上,且PM DN =.（1）求证：直线//MN 平面PCD ；（2）若M 为线段PA 中点,求直线PB 与平面AMN 所成的角的余弦值. 8．如图,三棱柱111ABC A B C -中,四边形11AA BB 是菱形,,二面角11C A B B --为6π, 1CB =. （Ⅰ）求证：平面1ACB ⊥平面1CBA ; （Ⅱ）求二面角1A AC B --的余弦值.9．如图,已知多面体EABCDF 的底面ABCD 是边长为2的正方形, EA ⊥底面ABCD , //FD EA ,且112FD EA ==．（Ⅰ）求多面体EABCDF 的体积；（Ⅱ）求直线EB 与平面ECF 所成角的正弦值；（Ⅲ）记线段BC 的中点为K ,在平面ABCD 内过点K 作一条直线与平面ECF 平行,要求保留作图痕迹,但不要求证明．10．如图,四棱锥P ABCD -中,侧面PAD ⊥底面ABCD , //AD BC , AD DC ⊥, 3AD DC ==, 2BC =,26PD PA ==,点F 在棱PG 上,且2FC FP =,点E 在棱AD 上,且//PA 平面BEF .（1）求证： PE ⊥平面ABCD ； （2）求二面角P EB F --的余弦值.11．如图所示的几何体中,ABC ∆内接于圆O ,且AB 是圆O 的直径,四边形DCBE 为矩形,且DC AB ⊥. (Ⅰ)证明:AD BC ⊥;(Ⅱ)若4,2AB BC ==且二面角A BD C --所成角θ5试求该几何体ABCDE 的体积.12. 已知四棱锥P ABCD-的底面是平行四边形,E F，分别是AD PC，的中点,EF BD⊥,22AP AB AD==,0=60BAD∠．（Ⅰ）求证：BD APB⊥面；（Ⅱ）若AB PB=,求二面角C BE F--的余弦值．FEABDCP13. 如图1,在ABC∆中,9036C BC AC∠︒＝，＝，＝,,D E分别是AC AB，上的点,且DE BC∥，2DE=.将ADE∆沿DE折起到1A DE∆的位置,使1AC CD⊥,如图2.（Ⅰ）M是1A D的中点,求CM与平面1A BE所成角的大小；（Ⅱ）求二面角1A BE C--的正切值.14. 如图,矩形CDEF所在平面与直角梯形ABCD所在平面垂直,其中//AB CD,11,22AB BC CD===,BC CD⊥,//MB FC,3MB FC==.P、Q分别为BC、AE的中点.（1）求证：//PQ平面MAB；（2）求二面角A EC D--的余弦值.15. 如图所示,棱柱111ABC A B C-为正三棱柱,且1AC C C=,其中点,F D分别为11,AC B B的中点.(1)求证://DF平面ABC;(2)求证:DF⊥平面1ACC;(3)求平面1DC A与平面ABC所成的锐二面角的余弦值CDFB1A1C1B16. 如图,在多面体ABCDEF中,底面ABCD是边长为2的菱形,∠BAD=60°,四边形BDEF是矩形,平面BDEF⊥平面ABCD,BF=3,H是CF的中点．（Ⅰ）求证：AF//平面BDH；（Ⅱ）求二面角A﹣FE﹣C的大小．。

数列1．已知等差数列满足，,则的值为____．2．在各项均为正数的等比数列{}n a 中，若21a =， 8646a a a =+，则3a 的值为_________.3．设数列{}n a 为等差数列, n S 为数列{}n a 的前n 项和,已知3159,225,n S S B ==为数列n S n ⎧⎫⎨⎬⎩⎭的前n 项和，则n B =__________．4．数列{}n a 为等比数列， 11a =且1351,4,7a a a +++成等差数列，则公差d =__________． 5．设数列{}n a 的首项11a =，且满足212121n n a a +-=+与2211n n a a -=+，则数列{}n a 的前20项和为__________．6．等比数列{}n a 中， 1473692,18a a a a a a ++=++=，则{}n a 的前9项和9S =__________． 7．设数列{}n a 满足2410a a +=,点(),n n P n a 对任意的n N +∈，都有向量()11,2n n P P +=,则数列{}n a 的前n 项和n S =__________．8．已知数列{}n α满足221221,2,1cos sin ,22n n n n a a a a ππ+⎛⎫===++ ⎪⎝⎭则该数列的前21项的和为__________．9．已知数列{}n a 的前n 项和n S 满足21n n S a =-，则1210181818=a a a -+-+-_______.10．已知各项都为整数的数列{}n a 中, 12a =，且对任意的*N n ∈，满足1122n n n a a +-<+,2n n a a +- 321n >⨯-，则2017a =__________．11．设等差数列{}n a 的前n 项和为n S ，若1378S =, 71210a a +=,则17a =_______; 12．设等比数列｛a n }中,S n 是前n 项和，若36270a a -=，则＝__________。

热点3 平面解析几何【名师精讲指南篇】【热点深度剖析】1. 平面解析几何在15-17年均是以填空题、解答题的形式进行考查，题目多为中高档题，着重考查学生运算求解能力、推理论证能力，涉及到等价转化和数形结合思想. 平面解析几何一般不与其它章节知识结合考查，常单独设置题目.2. 对于解析几何的复习，一、“直线与方程”和“圆的方程”是高考C级考点，考查频率高，考查知识点较多，但试题不一定有难度，复习时要在解题中注意数形结合，体会代数与几何的相互转化方法，二、圆锥曲线涉及的基本量较多，关系有差异但较为相似，不可张冠李戴，三、运算求解能力是基本能力，它会制约整个解题过程.复习中加强计算能力的培养，特别是在带字母的运算中，不仅要关注算，更重要的是关注算理，四、处理圆锥曲线的核心方法是将涉及的几何问题代数化，通过代数运算解决几何问题，加强对问题的代数转化能力.3. 预计18年考查直线的方程，点到直线距离，直线与圆的位置关系，椭圆的标准方程与几何性质的可能性较大.直线的斜率与倾斜角，直线的平行关系与垂直关系，双曲线的标准方程与几何性质也有可能考查．【最新考纲解读】【重点知识整合】一、1.椭圆的定义：（1）第一定义：平面内到两定点F1,F2的距离之和为定值2a(2a>|F1F2|)的点的轨迹. （2）第二定义：平面内与定点和直线的距离之比为定值e的点的轨迹.（0<e<1）.2.图形与方程（以一个为例）图形标准方程：12222=+by a x (b a >>0)3. 几何性质：（1）范围 ,a x a b y b -≤≤-≤≤ （2）中心 坐标原点(0,0)O（3）顶点 (,0),(,0),(0,),(0,)a a b b --（4）对称轴 x 轴，y 轴，长轴长2a ，短轴长2b（5）焦点 12(,0),(,0)F c F c - 焦距 2c ，（c = （6）离心率 ce a=，（01e <<） （7）准线 2a x c=±（8）焦半径 00,r a ex r a ex =+=-左右（9）通径 22b a（10）焦参数 2a c二、1.双曲线的定义：（1）第一定义：平面内到两定点F 1,F 2的距离之差的绝对值为定值2a(2a ＜|F 1F 2|)的点的轨迹. （2）第二定义：平面内与定点和直线的距离之比为定值e 的点的轨迹.（e ＞1）. 2.图形与方程（以一个为例） 图形标准方程：22221(0,0)x y a b a b-=>>3. 几何性质：（1）范围 x a ≥，y R ∈ （2）中心 坐标原点(0,0)O （3）顶点 (,0),(,0)a a -（4）对称轴 x 轴，y 轴，实轴长2a ，虚轴长2b（5）焦点 12(,0),(,0)F c F c - 焦距 2c ，（c = （6）离心率 ce a=，（01e <<） （7）准线 2a x c=±（8）焦半径 00,r ex a r ex a =+=-左右（9）通径 22b a（10）焦参数 2a c三、1. 抛物线的定义：平面内与定点和直线的距离相等的点的轨迹. （e =1） 2.图形与方程（以一个为例） 图形标准方程：22(0)y px p => 3. 几何性质：（1）范围 0x ≥经，y R ∈ （2）中心 无 （3）顶点 (0,0)O（4）对称轴 x 轴 （5）焦点 (,0)2pF 焦距 无 （6）离心率 1e = （7）准线 2p x =-（8）焦半径 02p r x =+ （9）通径 2p （10）焦参数 p 【应试技巧点拨】一、（1）要能够灵活应用圆锥曲线的两个定义（及其“括号”内的限制条件）解决有关问题，如果涉及到其两焦点(或两相异定点)，那么优先选用圆锥曲线第一定义；如果涉及到焦点三角形的问题，也要重视第一定义和三角形中正余弦定理等几何性质的应用，尤其注意圆锥曲线第一定义与配方法的综合运用。