新人教版数学八年级上册13.3.2第2课时 含30°角的直角三角形的性质精品导学案

第十三章轴对称13.3 等腰三角形13.3.2 等边三角形第2课时含30°角的直角三角形的性质一、教学目标1.掌握含有30°角的直角三角形的性质.2.经历探索含有30°角的直角三角形性质的过程，并运用其进行有关的证明和计算.二、教学重难点重点：含有30°角的直角三角形的性质.难点：运用含有30°角的直角三角形的性质进行计算和证明．三、教学过程【新课导入】[复习导入]教师带领学生复习等腰三角形和等边三角形的性质与判定，为本节课的学习做准备.【新知探究】知识点含30°角的直角三角形的性质[提出问题]用直尺量一量含有30°角的直角三角板的最短直角边（也即是30°角所对的直角边）与斜边的长度，你有什么发现吗？[动手操作]学生量一下自己手里的含有30°角的直角三角板，将所量得的结果记录在练习本上，由于每个学生的三角板并不完全一样，所以学生量得的结果会各不相同.教师点名5位学生回答他们的测量结果，并将测量结果写在黑板上.[课件展示]教师利用多媒体展示如下三位学生的结果：引导学生观察，斜边长与最短的直角边长存在什么关系(2倍关系）.之后再验证黑板上学生的测量结果，发现也符合这样的倍数关系.[提出问题]如图，将两个相同的含30°角的三角尺摆放在一起.你能借助这个图形，找到Rt △ABC 的直角边BC 与斜边AB 之间的数量关系吗？[课件展示]教师利用多媒体展示如下动画过程：[小组讨论]学生之间讨论，教师引导学生观察，两个相同的含30°角的三角尺摆放在一起是什么图形，进而得到结论.之后教师点名，由代表回答小组间讨论的结果.教师纠正.[课件展示]教师利用多媒体展示如下证明过程：如图，△ADC 是△ABC 的轴对称图形，因此AB=AD, ∠BAD=2×30°=60°，从而△ABD 是一个等边三角形.再由AC ⊥BD,可得BC=CD= 12 AB.[提出问题]由此我们可以得到什么结论呢？[学生回答]学生的可能回答有：生甲：30°角所对的直角边的长度是斜边长度的一半.生乙：最短的直角边的长度乘以2就是斜边的长度.对于学生的回答，只要意思对，都给予肯定，但如乙同学的回答，这里教师应强调，应加上“含30°角的直角三角形中”.[提出问题]如何验证你们的猜想呢？[课件展示]教师利用多媒体展示如下已知与求证：已知：如图，在Rt △ABC 中，∠C=90°，∠A=30°.求证：BC= 12AB ．[小组讨论]学生之间讨论，之后每位学生在练习本上书写证明过程，教师巡视，及时订正学生的错误.[课件展示]教师利用多媒体展示如下证明过程：证法一：证明：在△ABC 中，∵∠C=90°，∠A=30°, ∴∠B=60°．如图，延长BC 到点D ，使BD=AB ，连接AD ，则△ABD 是等边三角形．又∵AC ⊥BD, ∴BC=12BD ．∴BC=12AB ．证法二：证明：在BA 上截取BE=BC ，连接EC.∵∠B= 60°，BE=BC.∴△BCE 是等边三角形，∴∠BEC= 60°，BE=EC.∵∠A= 30°，∴∠ECA=∠BEC-∠A=60°-30° = 30°.∴AE=EC ，∴AE=BE=BC ，∴AB=AE+BE=2BC ，即BC=12AB ．[归纳总结]在直角三角形中，如果一个锐角等于30°，那么它所对的直角边等于斜边的一半.该性质的几何语言：在Rt △ABC 中，∵∠C=90°，∠A=30°，∴BC=12AB ．并提醒学生注意：该性质是“含有30°角的直角三角形”所特有的，一般的直角三角形没有这个性质.[课件展示]教师利用多媒体展示如下例题：例1 如图是屋架设计图的一部分，点D 是斜梁AB 的中点，立柱BC ，DE 垂直于横梁AC ，AB=7.4m ，∠A=30°，立柱BC,DE 要多长？解：∵DE ⊥AC,BC ⊥AC,∠A=30 °，∴BC=12AB,DE=12AD.∴BC=12×7.4=3.7(m).又AD=12AB,∴DE=12AD=12×3.7=1.85(m).答：立柱BC 的长是3.7m ，DE 的长是1.85m.例2 如图，在Rt △ABC 中，CD 是斜边AB 上的高，∠B=30°.（1）若CD=8cm ，则BC 的长度是多少？（2）若AD=3cm ，则AB 的长度是多少？解：（1）∵CD 是斜边AB 边上的高，∴∠BDC=90°.∵在Rt △BCD 中，∠B=30°，CD=8cm ，∴BC=2CD=16cm.（2）在Rt △ABC 中，∵∠B=30°，∴∠A=60°，∵CD 是斜边AB 边上的高，∴∠ADC=90°.∴∠ACD=30°.∵在Rt △ACD 中，∠ACD=30°，AD=3cm ，∴AC=2AD=6cm.∵在Rt △ABC 中，∠B=30°，AC=6cm ，∴AB=2AC=12cm.[归纳总结]注意：运用含30°角的直角三角形的性质求线段长时，要分清线段所在的直角三角形．[课件展示]教师利用多媒体展示如下例题：例3 (2021•宣城模拟)如图，在△ABC中,∠ACB=90°，∠B=15°,DE垂直平分AB，交BC于点E,AE=6cm,则AC=( D )A.6cmB.5cmC.4cmD.3cm[归纳总结]含30°角的直角三角形的性质是求线段长度和证明线段之间倍分关系的重要工具，解题时，一般先是寻找30°角所在的直角三角形，得到斜边与直角边的关系，当30°角不在一个直角三角形中时，可考虑作辅助线构造含30°角的直角三角形,如：作垂线得到含30°角的直角三角形，或作等腰三角形构造顶角的邻补角为60°.当三角形中含有15°，30°，60°，120°角时，也可通过添加辅助线，构造含30°角的直角三角形求解.常见的模型有如下几种（图中所标的红色的角均为30°）：【课堂小结】【课堂训练】1.如图,在△ABC中, AD是边BC的垂直平分线，∠B=60°,BD=2 ,那么AC的长度是( D )A.1B.2C.3D.42.如图,在△ABC中，∠C=60°, AD是BC边上的高,点E为AD的中点,连接BE并延长交AC于点F .若∠AFB=90°, EF=2，则BF长为( D )A.4B.6C.8D.103.(2021•乌苏市二模)如图,在等边△ABC中, D是AB的中点，DE⊥AC于点E,EF⊥BC于点F ,已知AB=8,则BF的长为( C )A.3B.4C.5D.64.如图，∠AOP＝∠BOP＝15°，PC∥OA交OB于点C，PD⊥OA于点D，若PC＝3，则PD等于( ) A．3 B．2C.1.5 D．1【解析】如图，过点P作PE⊥OB于点E.∵PC∥OA，∴∠AOP＝∠CPO＝15°，∴∠PCE＝∠BOP＋∠CPO ＝15°＋15°＝30°.又∵PC＝3，∴PE＝1.5.∵∠AOP＝∠BOP，PD⊥OA，∴PD＝PE＝1.5.故选C.5.在△ABC中,∠A: ∠B: ∠C=1:2:3,若AB=10,则BC= 5 .6.如图，在△ABC中，AB=BC ,∠ABC=120°，过点B作BD⊥BC，交AC于点D，若AD=1 ,则CD的长度为 2 ．7.在△ABC中，AB=AC，∠BAC=120°，D是BC的中点，DE⊥AB于点E，求证：BE=3EA.证明：∵AB=AC，∠BAC=120°，∴∠B=∠C=30°.∵D是BC的中点，∴AD⊥BC.∴∠ADC=90°，∠BAD=∠DAC=60°.∴AB=2AD.∵DE⊥AB，∴∠AED=90°，∴∠ADE=30°，∴AD=2AE.∴AB=4AE，∴BE=3AE.8.求证:有一个锐角是30°的直角三角形斜边上的高把斜边分成1:3的两条线段.已知:如图，在Rt△ABC中，∠C=90°,∠A=30°, CD⊥AB.求证:BD:AD=1:3.证明:在Rt△ABC中,∠C=90°，∠A=30°，∴AB=2BC , ∠B=90-30°=60° ,∵CD⊥AB ,∴∠CDB=90° ,∴∠BCD=30° ,∴BC=2BD .∴AB=4BD,∴BD：AD=1：3.故有一个锐角是30°的直角三角形斜边上的高把斜边分成1：3的两条线段.9.如图，在Rt△ABC中，CM平分∠ACB交AB于点M，过点M作MN//BC交AC于点N，且MN平分∠AMC，若AN=1，求BC的长.解：∵CM平分∠ACB，MN平分∠AMC,∴∠NCM=∠BCM，∠AMN=∠NMC.∵MN//BC，∴∠AMN=∠B，∠NMC=∠BCM.∴∠AMN=∠B=∠NMC=∠BCM=∠NCM. ∴NM=NC.∵∠ACB=∠NCM+∠BCM，∴∠ACB=2∠B.∵∠A=90°，∴∠ACB+∠B=90°，∴∠B=30°.∴∠AMN=∠B=30°.∵∠A=90°，∠AMN=30°，AN=1,∴MN=2.∵AC=AN+NC=AN+MN=3，∴BC=2AC=6.【教学反思】本节课我采用动手测量含30°角的直角三角板的最短直角边长和斜边长的方式入手，因为学生的三角尺尺寸不用，所以学生测量了不同大小的含30°的直角三角板,再将测量数据进行比较，从而直观、快捷地找出它们的关系.这样就避免了以往由于知识比较抽象学生无从下手,无法理解的情况。

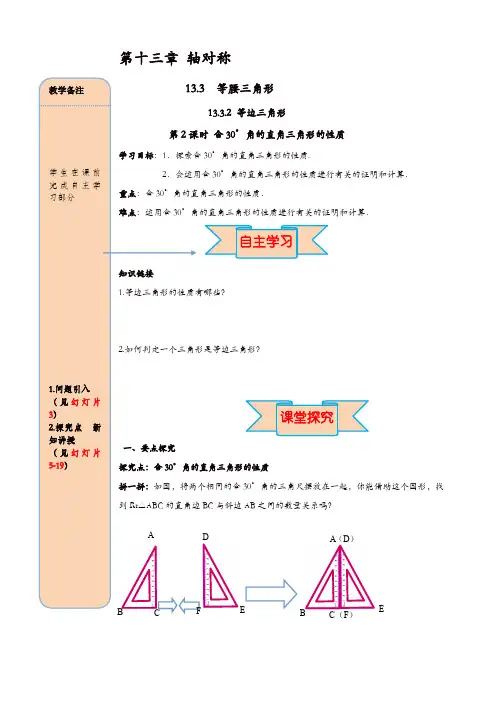
第十三章 轴对称等腰三角形13.3.2 等边三角形含30°角的直角三角形的性质30°角的直角三角形的性质.30°角的直角三角形的性质进行有关的证明和计算．30°角的三角尺摆放在一起，你能借助这个图形，找BC 与斜边AB 之间的数量关系吗？DFBCA （D ） BC （F ）E填一填：∠A=∠D=_______，⇒∠BAC=___________;AB=DE,⇒△ABE 是__________三角形；⇒2BC=BE=________.要点归纳： 在直角三角形中，如果一个锐角等于30°，那么它所对的直角边等于斜边的一半. 证一证：已知：如图，在Rt △ABC 中，∠C =90°，∠A =30°. 求证：BC=12AB. 方法一：倍长法【提示：延长BC 至D ，使CD=BD ，连接AD 】 证明：方法二：截半法【提示：在BA 上截取BE=BC ，连接EC 】 证明：方法总结在证明线段之间的和差倍分关系时，倍长法与截半法是常用的两种作辅助线的方法.例1：如图，在Rt △ABC 中，∠ACB ＝90°，∠B ＝30°，CD 是斜边AB 上的高，AD ＝3cm ，则AB 的长度是( )A ．3cmB ．6cmC ．9cmD ．12cm注意：运用含30°角的直角三角形的性质求线段长时，要分清线段所在的直角三角形．ABC例2：如图，∠AOP ＝∠BOP ＝15°，PC ∥OA 交OB 于C ，PD ⊥OA 于D ，若PC ＝3，则PD 等于( )A ．3B ．2 C.1.5 D ．1方法总结：含30°角的直角三角形与角平分线、垂直平分线的综合运用时，关键是寻找或作辅助线构造含30°角的直角三角形．例3 如图，在△ABC 中，∠C ＝90°，AD 是∠BAC 的平分线，过点D 作DE ⊥AB ，DE 恰好是∠ADB 的平分线．CD 与DB 有怎样的数量关系？请说明理由．方法总结：含30°角的直角三角形的性质是表示线段倍分关系的一个重要的依据，如果问题中出现探究线段倍分关系的结论时，要联想此性质．例4：已知等腰三角形的底角为15°，腰长为20.求腰上的高.方法总结：在求三角形边长的一些问题中，可以构造含30°角的直角三角形解决．本题的关键是作高，而后利用等腰三角形及外角的性质，得出30°角，利用含30°角的直角三角形的性质解决问题.1.在Rt △ABC 中，CD 是斜边AB 上的高，∠B ＝30°，AD ＝2cm ，则AC 的长是( ) A ．2 cm B ．4 cm C ．6 cm D ．8 cm2.如图，在△ABC 中，∠C ＝90°，∠B ＝30°，AD 平分∠CAB ，交BC 于点D ，若CD ＝1，则BD ＝____．第2题图第3题图3.如图是某商场一楼与二楼之间的手扶电梯示意图，其中AB，CD分别表示一楼、二楼地面的水平线，∠ABC＝150°，BC的长是8m，则乘电梯从点B到点C上升的高度h＝____ m.4.如图所示，已知△ABC中，∠ACB=90°，CD⊥AB于点D，∠A=30°.求证：AB=4BD证明：∵△ABC中，∠ACB=90°，∠A=30∴BC= AB∠B=又∵△BCD中,CD⊥AB∴∠BCD=∴BD= BC∴BD= AB即.5.如图所示,∠AOP=∠BOP=15°,PC∥OA,PD⊥OA,若PC=4.求PD的长.二、课堂小结含30°角的直角三角形的性质：应用的前提在三角形中，结论是30°角所对的直角边是的一半，而不是任一直角边是斜边的一半．第1题图第2题图2.某市在旧城改造中，计划在一块如图所示的△ABC空地上种植草皮以美化环境，8.如图，已知△ABC是等边三角形，D,E分别为BC、AC上的点，且CD=AE，AD、BE相交于点P，BQ⊥AD于点Q,求证BP=2PQ.。

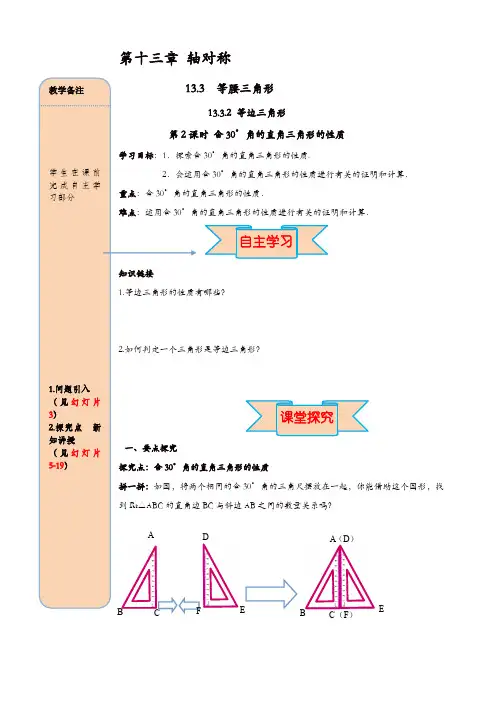
第十三章 轴对称等腰三角形13.3.2 等边三角形含30°角的直角三角形的性质30°角的直角三角形的性质.30°角的直角三角形的性质进行有关的证明和计算．30°角的三角尺摆放在一起，你能借助这个图形，找BC 与斜边AB 之间的数量关系吗？DFBCA （D ） BC （F ）E填一填：∠A=∠D=_______，⇒∠BAC=___________;AB=DE,⇒△ABE 是__________三角形；⇒2BC=BE=________.要点归纳： 在直角三角形中，如果一个锐角等于30°，那么它所对的直角边等于斜边的一半. 证一证：已知：如图，在Rt △ABC 中，∠C =90°，∠A =30°. 求证：BC=12AB. 方法一：倍长法【提示：延长BC 至D ，使CD=BD ，连接AD 】 证明：方法二：截半法【提示：在BA 上截取BE=BC ，连接EC 】 证明：方法总结在证明线段之间的和差倍分关系时，倍长法与截半法是常用的两种作辅助线的方法.例1：如图，在Rt △ABC 中，∠ACB ＝90°，∠B ＝30°，CD 是斜边AB 上的高，AD ＝3cm ，则AB 的长度是( )A ．3cmB ．6cmC ．9cmD ．12cm注意：运用含30°角的直角三角形的性质求线段长时，要分清线段所在的直角三角形．ABC例2：如图，∠AOP ＝∠BOP ＝15°，PC ∥OA 交OB 于C ，PD ⊥OA 于D ，若PC ＝3，则PD 等于( )A ．3B ．2 C.1.5 D ．1方法总结：含30°角的直角三角形与角平分线、垂直平分线的综合运用时，关键是寻找或作辅助线构造含30°角的直角三角形．例3 如图，在△ABC 中，∠C ＝90°，AD 是∠BAC 的平分线，过点D 作DE ⊥AB ，DE 恰好是∠ADB 的平分线．CD 与DB 有怎样的数量关系？请说明理由．方法总结：含30°角的直角三角形的性质是表示线段倍分关系的一个重要的依据，如果问题中出现探究线段倍分关系的结论时，要联想此性质．例4：已知等腰三角形的底角为15°，腰长为20.求腰上的高.方法总结：在求三角形边长的一些问题中，可以构造含30°角的直角三角形解决．本题的关键是作高，而后利用等腰三角形及外角的性质，得出30°角，利用含30°角的直角三角形的性质解决问题.1.在Rt △ABC 中，CD 是斜边AB 上的高，∠B ＝30°，AD ＝2cm ，则AC 的长是( ) A ．2 cm B ．4 cm C ．6 cm D ．8 cm2.如图，在△ABC 中，∠C ＝90°，∠B ＝30°，AD 平分∠CAB ，交BC 于点D ，若CD ＝1，则BD ＝____．第2题图第3题图3.如图是某商场一楼与二楼之间的手扶电梯示意图，其中AB，CD分别表示一楼、二楼地面的水平线，∠ABC＝150°，BC的长是8m，则乘电梯从点B到点C上升的高度h＝____ m.4.如图所示，已知△ABC中，∠ACB=90°，CD⊥AB于点D，∠A=30°.求证：AB=4BD证明：∵△ABC中，∠ACB=90°，∠A=30∴BC= AB∠B=又∵△BCD中,CD⊥AB∴∠BCD=∴BD= BC∴BD= AB即.5.如图所示,∠AOP=∠BOP=15°,PC∥OA,PD⊥OA,若PC=4.求PD的长.二、课堂小结含30°角的直角三角形的性质：应用的前提在三角形中，结论是30°角所对的直角边是的一半，而不是任一直角边是斜边的一半．第1题图第2题图2.某市在旧城改造中，计划在一块如图所示的△ABC空地上种植草皮以美化环境，8.如图，已知△ABC是等边三角形，D,E分别为BC、AC上的点，且CD=AE，AD、BE相交于点P，BQ⊥AD于点Q,求证BP=2PQ.。

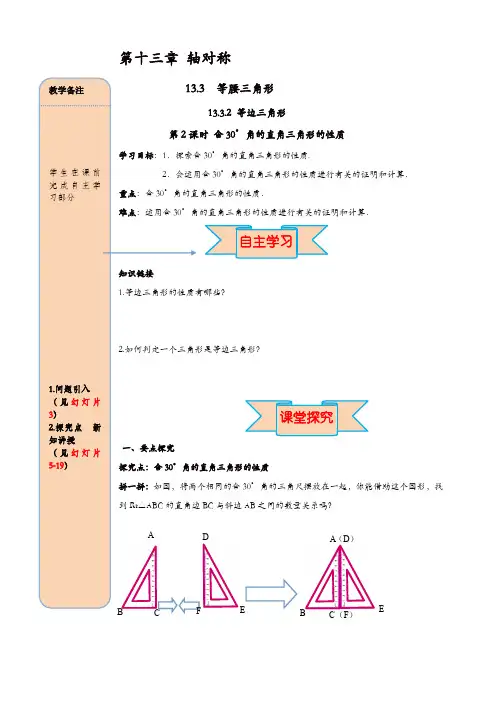
第十三章 轴对称等腰三角形13.3.2 等边三角形含30°角的直角三角形的性质30°角的直角三角形的性质.30°角的直角三角形的性质进行有关的证明和计算．30°角的三角尺摆放在一起，你能借助这个图形，找BC 与斜边AB 之间的数量关系吗？DFBCA （D ） BC （F ）E填一填：∠A=∠D=_______，⇒∠BAC=___________;AB=DE,⇒△ABE 是__________三角形；⇒2BC=BE=________.要点归纳： 在直角三角形中，如果一个锐角等于30°，那么它所对的直角边等于斜边的一半. 证一证：已知：如图，在Rt △ABC 中，∠C =90°，∠A =30°. 求证：BC=12AB. 方法一：倍长法【提示：延长BC 至D ，使CD=BD ，连接AD 】 证明：方法二：截半法【提示：在BA 上截取BE=BC ，连接EC 】 证明：方法总结在证明线段之间的和差倍分关系时，倍长法与截半法是常用的两种作辅助线的方法.例1：如图，在Rt △ABC 中，∠ACB ＝90°，∠B ＝30°，CD 是斜边AB 上的高，AD ＝3cm ，则AB 的长度是( )A ．3cmB ．6cmC ．9cmD ．12cm注意：运用含30°角的直角三角形的性质求线段长时，要分清线段所在的直角三角形．ABC例2：如图，∠AOP ＝∠BOP ＝15°，PC ∥OA 交OB 于C ，PD ⊥OA 于D ，若PC ＝3，则PD 等于( )A ．3B ．2 C.1.5 D ．1方法总结：含30°角的直角三角形与角平分线、垂直平分线的综合运用时，关键是寻找或作辅助线构造含30°角的直角三角形．例3 如图，在△ABC 中，∠C ＝90°，AD 是∠BAC 的平分线，过点D 作DE ⊥AB ，DE 恰好是∠ADB 的平分线．CD 与DB 有怎样的数量关系？请说明理由．方法总结：含30°角的直角三角形的性质是表示线段倍分关系的一个重要的依据，如果问题中出现探究线段倍分关系的结论时，要联想此性质．例4：已知等腰三角形的底角为15°，腰长为20.求腰上的高.方法总结：在求三角形边长的一些问题中，可以构造含30°角的直角三角形解决．本题的关键是作高，而后利用等腰三角形及外角的性质，得出30°角，利用含30°角的直角三角形的性质解决问题.1.在Rt △ABC 中，CD 是斜边AB 上的高，∠B ＝30°，AD ＝2cm ，则AC 的长是( ) A ．2 cm B ．4 cm C ．6 cm D ．8 cm2.如图，在△ABC 中，∠C ＝90°，∠B ＝30°，AD 平分∠CAB ，交BC 于点D ，若CD ＝1，则BD ＝____．第2题图第3题图3.如图是某商场一楼与二楼之间的手扶电梯示意图，其中AB，CD分别表示一楼、二楼地面的水平线，∠ABC＝150°，BC的长是8m，则乘电梯从点B到点C上升的高度h＝____ m.4.如图所示，已知△ABC中，∠ACB=90°，CD⊥AB于点D，∠A=30°.求证：AB=4BD证明：∵△ABC中，∠ACB=90°，∠A=30∴BC= AB∠B=又∵△BCD中,CD⊥AB∴∠BCD=∴BD= BC∴BD= AB即.5.如图所示,∠AOP=∠BOP=15°,PC∥OA,PD⊥OA,若PC=4.求PD的长.二、课堂小结含30°角的直角三角形的性质：应用的前提在三角形中，结论是30°角所对的直角边是的一半，而不是任一直角边是斜边的一半．第1题图第2题图2.某市在旧城改造中，计划在一块如图所示的△ABC空地上种植草皮以美化环境，已知∠8.如图，已知△ABC是等边三角形，D,E分别为BC、AC上的点，且CD=AE，AD、BE相交于点P，BQ⊥AD于点Q,求证BP=2PQ.。

第2课时含30°角的直角三角形的性质一、学习目标1、理解含30°锐角的直角三角形的性质；2、能利用含30°锐角的直角三角形的性质解决简单的实际问题。

二、温故知新（口答）1、等边三角形三边，三个角都等于，2、等边三角形是轴对称图形,它有条对称轴，它的对称轴。

三、自主探究合作展示探究（一）1、如图（1），将两个含有30°角的三角形放在一起，形，找到Rt△ABC的直角边BC与斜边AB图（1）B C D2、你能用所学的知识验证以上结论吗？方法1：如图(2)，△ABC是等边三角形，AD⊥BC于D，∠BAD= °,BD= BC= AB。

方法2：如图(3)，△ABC中，延长BC到D使BD=AB，连接AD，则△ABD是三角形,BC=12 =12。

ACBD图（2）BADC图（3）探究（二）例题：如图（4）是屋架设计图的一部分，点D 是斜梁AB 的中点，立柱BC 、DE 垂直于横梁AC ，AB=7.4m ，∠A=30°，立柱BC 、DE 要多长？分析：观察图形可以发现在Rt △AED 与Rt △ACB 中，由于∠A=30°，所以DE= ，BC= ，又由D 是AB的中点，所以DE= ．例题反思：探究（三）D CA EB图（4）例题：如图（5），要把一块三角形的土地均匀分给甲、乙、丙三家农户去种植,如果∠C ＝90°，∠A ＝30°,要使这三家农户所得土地的大小和形状都相同,请你试着分一分,在图上画出.例题反思：四、双基检测1、等腰三角形中，一腰上的高与底边的夹角为30°，则此三角形中腰与底边的关系（ ）A 、腰大于底边B 、腰小于底边A┓CA图（5）C 、腰等于底边D 、不能确定2、在Rt △ABC 中，∠C=90度，∠A=30°，CD ⊥AB 于点D ，AB=8cm,则BC= ， BD= ， AD=3、如图（6）,在△ABC 中∠C=90°,∠B=15°,AB 的垂直平分线交BC 于D,交AB 于M,且BD=8㎝,求AC 之长.五、学习反思请你对照学习目标，谈一下这节课的收获及困惑。

第2课时含30°角的直角三角形的性质1．理解并掌握含30°角的直角三角形的性质定理．(重点)2．能灵活运用含30°角的直角三角形的性质定理解决有关问题．(难点)一、情境导入问题：1．我们学习过直角三角形，直角三角形的角之间都有什么数量关系？2．用你的30°角的直角三角尺，把斜边和30°角所对的直角边量一量，你有什么发现？今天，我们先看一个特殊的直角三角形，看它的边角具有什么性质．二、合作探究探究点：含30°角的直角三角形的性质【类型一】利用含30°角的直角三角形的性质求线段长如图，在Rt△ABC中，∠ACB＝90°，∠B＝30°，CD是斜边AB上的高，AD＝3cm，则AB的长度是( )A．3cm B．6cm C．9cm D．12cm解析：在Rt△ABC中，∵CD是斜边AB上的高，∴∠ADC＝90°，∴∠ACD＝∠B ＝30°.在Rt△ACD中，AC＝2AD＝6cm，在Rt△ABC中，AB＝2AC＝12cm.∴AB的长度是12cm.故选D.方法总结：运用含30°角的直角三角形的性质求线段长时，要分清线段所在的直角三角形．【类型二】如图，∠AOP ＝∠BOP ＝15°，PC ∥OA 交OB 于C ，PD ⊥OA 于D ，若PC ＝3，则PD 等于( )A ．3B ．2C ．1.5D ．1解析：如图，过点P 作PE ⊥OB 于E ，∵PC ∥OA ，∴∠AOP ＝∠CPO ，∴∠PCE ＝∠BOP ＋∠CPO ＝∠BOP ＋∠AOP ＝∠AOB ＝30°.又∵PC ＝3，∴PE ＝12PC ＝12×3＝1.5.∵∠AOP ＝∠BOP ，PD ⊥OA ，∴PD ＝PE ＝1.5.故选C.方法总结：含30°角的直角三角形与角平分线、垂直平分线的综合运用时，关键是寻找或作辅助线构造含30°角的直角三角形．【类型三】 利用含30°角的直角三角形的性质探究线段之间的倍、分关系如图，在△ABC 中，∠C ＝90°，AD 是∠BAC 的平分线，过点D 作DE ⊥AB .DE 恰好是∠ADB 的平分线．CD 与DB 有怎样的数量关系？请说明理由．解析：由条件先证△AED ≌△BED ，得出∠BAD ＝∠CAD ＝∠B ，求得∠B ＝30°，即可得到CD ＝12DB . 解：CD ＝12DB .理由如下：∵DE ⊥AB ，∴∠AED ＝∠BED ＝90°.∵DE 是∠ADB 的平分线，∴∠ADE ＝∠BDE .又∵DE ＝DE ，∴△AED ≌△BED (ASA)，∴AD ＝BD ，∠DAE＝∠B .∵∠BAD ＝∠CAD ＝12∠BAC ，∴∠BAD ＝∠CAD ＝∠B .∵∠BAD ＋∠CAD ＋∠B ＝90°，∴∠B ＝∠BAD ＝∠CAD ＝30°.在Rt △ACD 中，∵∠CAD ＝30°，∴CD ＝12AD ＝12BD ，即CD ＝12DB . 方法总结：含30°角的直角三角形的性质是表示线段倍分关系的一个重要的依据，如果问题中出现探究线段倍分关系的结论时，要联想此性质．【类型四】 利用含30°角的直角三角形解决实际问题某市在“旧城改造”中计划在市内一块如图所示的三角形空地上种植某种草皮以美化环境，已知AC ＝50m ，AB ＝40m ，∠BAC ＝150°，这种草皮每平方米的售价是a 元，求购买这种草皮至少需要多少元？解析：作BD ⊥CA 交CA 的延长线于点D .在Rt △ABD 中，利用30°角所对的直角边是斜边的一半求BD ，即△ABC 的高．运用三角形面积公式计算面积求解．解：如图所示，作BD ⊥CA 于D 点．∵∠BAC ＝150°，∴∠DAB ＝30°.∵AB ＝40m ，∴BD ＝12AB ＝20m ，∴S △ABC ＝12×50×20＝500(m 2)．已知这种草皮每平方米a 元，所以一共需要500a 元．方法总结：解此题的关键在于作出CA 边上的高，根据相关的性质推出高BD 的长度，正确的计算出△ABC 的面积．三、板书设计含30°角的直角三角形的性质性质：在直角三角形中，如果一个锐角是30°，那么它所对的直角边等于斜边的一半．本节课借助于教学活动的开展，有效地激发了学生的探究热情和学习兴趣，从而引导学生通过自主探究以及合作交流等活动探究并归纳出本节课所学的新知识，促进了学生思维能力的提高．不足之处是部分学生的综合运用知识解决问题的能力还有待于在今后的教学和作业中进行进一步的训练和提高．。

第2课时含30°角的直角三角形的性质知识点含30 °角的直角三角形的性质1．在Rt△ABC中，∠C＝90°，∠B＝30°，AC＝4，则AB等于()A．2 B．4 C．6 D．82．如图13－3－41，在△ABC中，∠B＝30°，BC的垂直平分线交AB于点E，垂足为D，CE平分∠ACB.若BE＝2，则AE的长为()图13－3－41A. 3 B．1 C. 2 D．23．如图13－3－42，一水库迎水坡AB的长度为20 m，斜坡与水平面的夹角α为30°，则迎水坡的高度是________m.图13－3－424．如图13－3－43，∠C＝90°，∠A＝30°，BD⊥AD于点D，DC∥AB，AB＝10 cm，求DC的长．图13－3－435．如图13－3－44，在Rt△ABC中，∠A＝90°，∠ABC＝2∠C，BD是△ABC的角平分线．求证：CD＝2AD.图13－3－446．如图13－3－45，已知∠AOB＝60°，点P在射线OA上，OP＝10，点M，N在射线OB上，PM＝PN.若MN＝2，则OM的长为()图13－3－45A．3 B．4 C．5 D．67．如图13－3－46所示，已知∠BAC＝30°，AG平分∠BAC，D是射线AG上的一点，DE⊥AC于点E，DH⊥AB于点H，DF∥AC，交AB于点F.若DF＝10 cm，求DE的长．图13－3－468．如图13－3－47，一艘轮船以15海里/时的速度由南向北航行，在A处测得小岛P在北偏西15°的方向上，两小时后，轮船在B处测得小岛P在北偏西30°的方向上，在小岛周围18海里内有暗礁．若轮船仍按原方向继续向前航行，则有无触礁的危险？图13－3－47教师详解详析1．D 2.B 3.104．解：∵BD ⊥AD ，∠A ＝30°，AB ＝10 cm ， ∴BD ＝12AB ＝5 cm.∵DC ∥AB ，∠C ＝90°，∴∠CBA ＝90°. ∵∠A ＝30°，∠BDA ＝90°，∴∠DBA ＝60°.∴∠CBD ＝∠CBA －∠DBA ＝90°－60°＝30°.∴DC ＝12BD ＝52cm.5．证明：∵在Rt △ABC 中，∠A ＝90°，∠ABC ＝2∠C ，∴∠ABC ＝60°，∠C ＝30°. 又∵BD 是△ABC 的角平分线， ∴∠ABD ＝∠DBC ＝30°＝∠C. ∴BD ＝CD.∵在Rt △ABD 中，∠A ＝90°，∠ABD ＝30°， ∴AD ＝12BD.∴AD ＝12CD ，即CD ＝2AD.6．B7．解：∵DF ∥AC ，∴∠HFD ＝∠BAC ＝30°. ∵DH ⊥AB ，DF ＝10 cm ， ∴HD ＝12DF ＝12×10＝5(cm)．∵AG 平分∠BAC ，D 是射线AG 上的一点，DH ⊥AB ，DE ⊥AC ，∴DE ＝DH ＝5 cm.8．解：如图，过点P 作PC ⊥AB ，垂足为C.由题意得∠APB ＝∠PBC―∠PAB ＝30°－15°＝15°， ∴∠APB ＝∠PAB.∴PB ＝AB. ∵AB ＝15×2＝30(海里)， ∴PB ＝AB ＝30海里．在Rt △PBC 中，∵∠PCB ＝90°，∠PBC ＝30°， ∴PC ＝12PB ＝15海里．又∵15海里<18海里，∴若轮船仍按原方向继续向前航行，有触礁的危险．。