洛伦兹变换的四维形式1四维空间的转动变换

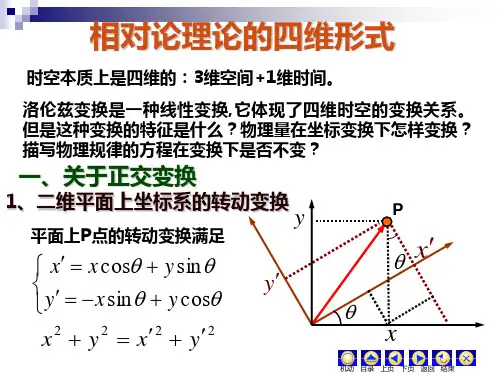
洛伦兹变换坐标系在狭义相对论中，洛伦兹变换是描述不同惯性参考系之间的时空坐标变换关系的数学表达式。

这种变换是由荷兰物理学家亨德里克·洛伦兹于1903年提出的，为描述高速运动下的物体和光传播等现象提供了重要的数学工具。

洛伦兹变换的基本原理狭义相对论认为，物体的运动状态和时间的流逝速度取决于观察者的参考系选择。

因此，为了描述同时存在的不同惯性参考系下的物理现象，需要进行坐标系之间的变换。

洛伦兹变换是这种坐标变换的数学表达形式。

洛伦兹变换的公式洛伦兹变换可以描述时间和空间坐标之间的转换关系。

在特殊相对论中，洛伦兹变换的一般形式可以表示为：x' = γ(x - vt)y' = yz' = zt' = γ(t - vx/c^2)其中，x、y、z、t是原来参考系中的空间坐标和时间，x’、y’、z’、t’是新的参考系中的空间坐标和时间，v表示两个参考系相对速度，c是光速，γ是洛伦兹因子。

洛伦兹因子洛伦兹因子γ定义为：γ = 1 / √(1 - v^2 / c^2)其中，v是参考系之间的相对速度。

当物体的速度远小于光速时，γ接近1，此时洛伦兹变换退化为经典的伽利略变换。

洛伦兹变换的重要性洛伦兹变换在描述高速运动下的物体以及光的传播等情况下起着重要作用。

它揭示了时空的弯曲性，探讨了观察者在不同惯性参考系中背景下所看到的物理现象之间的联系。

洛伦兹变换为狭义相对论的建立奠定了坚实的数学基础。

总结洛伦兹变换是描述不同惯性参考系之间的时空坐标变换关系的重要工具。

通过公式和洛伦兹因子，我们可以准确地描述高速运动物体和光的传播等现象，揭示了时空的规则和物质之间的联系。

因此，洛伦兹变换在现代物理学中具有重要的地位和作用。

第三节 洛伦兹变换式教学内容：1. 洛伦兹变换式的推导；2. 狭义相对论的时空观：同时性的相对性、长度的收缩和时间的延缓； 重点难点：狭义相对论时空观的主要结论。

基本要求：1. 了解洛伦兹坐标变换和速度变换的推导；2. 了解狭义相对论中同时性的相对性以及长度收缩和时间延缓概念；3. 理解牛顿力学中的时空观和狭义相对论中的时空观以及两者的差异。

三、洛伦兹坐标变换的推导()()⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧--='='='--='22211c v c vx t t z z y y c v vt x x 或 ()()⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧-'+'='='=-'+'=22211c v c x v t t z z y y c v t v x x据狭义相对论的两个基本假设来推导洛仑兹变换式。

1. 时空坐标间的变换关系作为一条公设，我们认为时间和空间都是均匀的，因此时空坐标间的变换必须是线性的。

对于任意事件P 在S 系和S '系中的时空坐标(x ，y ，z ，t )、(x '，y '，z '，t ')，因S ' 相对于S 以平行于 x 轴的速度v 作匀速运动，显然有y '=y , z '=z 。

在S 系中观察S 系的原点，x =0；在S '系中观察该点，x '=-v t '，即x '+v t '=0。

因此x =x '+v t '。

在任意的一个空间点上，可以设：x =k （x '+v t '），k 是—比例常数。

同样地可得到：x '=k '（x -v t ）= k '（x +(-v )t ）根据相对性原理，惯性系S 系和S '系等价，上面两个等式的形式就应该相同（除正、负号），所以k =k '。

洛伦兹变换推导过程详细全文共四篇示例，供您参考第一篇示例：洛伦兹变换（Lorentz transformation）是狭义相对论中的重要概念，描述了不同惯性参考系之间的时空坐标变换关系。

由荷兰物理学家亨德里克·安杰洛·洛伦兹（Hendrik Antoon Lorentz）首先提出，并由爱因斯坦在他的狭义相对论中进一步发展。

洛伦兹变换不仅在相对论中有着广泛的应用，而且也成为了后来爱因斯坦提出的广义相对论中的基础之一。

在这篇文章中，我们将详细推导洛伦兹变换的过程，并探讨其物理意义。

我们从狭义相对论的两个基本假设开始。

第一个假设是等效原理，即在加速度为零的惯性参考系中的物理定律是相同的。

第二个假设是光速不变原理，即光在真空中的传播速度对于所有惯性观察者都是相同的，不受光源或观察者的运动状态的影响。

根据这两个假设，我们可以推导出洛伦兹变换。

假设有两个惯性参考系S和S'，S'相对于S以速度v沿x轴方向匀速运动。

在S参考系中，事件的时空坐标为(x, y, z, t)，而在S'参考系中为(x', y', z', t')。

我们希望通过洛伦兹变换找到这两个参考系之间的坐标变换关系。

首先考虑S'参考系中的时间坐标t'和空间坐标x'之间的变换。

由光速不变原理可知，在S'参考系中静止的光源发出的光信号在空间中传播的速度是恒定不变的，即光速c。

假设光源在S参考系中坐标为(x, t)，在S'参考系中坐标为(x', t')，那么光信号在S参考系中的传播距离为c(t-t')，在S'参考系中的传播距离为c(t'-t)。

根据光速不变原理，这两个传播距离应该相等，即：c(t-t') = c(t'-t)整理得到：t' = γ(t - vx/c^2)其中γ为洛伦兹因子，定义为1/√(1-v^2/c^2)，即：γ = 1/√(1-v^2/c^2)这个式子描述了S'参考系中事件的时间与S参考系中事件的时间之间的关系。

洛伦兹变换编辑由于爱因斯坦提出的假说否定了伽利略变换，因此需要寻找一个满足相对论基本原理的变换式。

洛伦兹导出了这个变换式，一般称它为洛伦兹变换式。

中文名洛伦兹变换外文名Lorentz transformation别称洛伦兹变换式提出者亨德里克·洛伦兹提出时间1904年应用学科数学适用领域范围狭义相对论目录1简介2理论3释义4推导▪公设一▪公设二▪过程▪另一种方式5区别6四维矢量改写1简介编辑洛伦兹变换（Lorentz transformation）是观测者在不同惯性参照系之间对物理量进行测量时所进行的转换关系，在数学上表现为一套方程组。

洛伦兹变换因其创立者——荷兰物理学家亨德里克·洛伦兹而得名。

洛伦兹变换最初用来调和19世纪建立起来的经典电动力学同牛顿力学之间的矛盾，后来成为狭义相对论中的基本方程组。

2理论编辑洛伦兹变换（Lorentz transformation）是狭义相对论中关于不同惯性系之间物理事件时空坐标变换的基本关系式。

设两个惯性系为S系和S′系，它们相应的笛卡尔坐标系彼此平行，S′系相对于S系沿x 方向运动，速度为v，且当t=t′=0时，S′系与S系的坐标原点重合，则事件在这两个惯性系的时空坐标之间的洛伦兹变换为式中，；c为真空中的光速。

其逆变换形式为不同惯性系中的物理定律必须在洛伦兹变换下保持形式不变。

19世纪后期建立了麦克斯韦方程组，标志着经典电动力学取得了巨大成功。

然而麦克斯韦方程组在经典力学的伽利略变换下并不是协变的。

由麦克斯韦方程组可以得到电磁波的波动方程，由波动方程解出真空中的光速是一个常数。

按照经典力学的时空观，这个结论应当只在某个特定的惯性参照系中成立，这个参照系就是以太。

其它参照系中测量到的光速是以太中光速与观察者所在参照系相对以太参照系的速度的矢量叠加。

然而1887年的迈克耳孙-莫雷实验测量不到地球相对于以太参照系的运动速度。

1904年，洛伦兹提出了洛伦兹变换用于解释迈克耳孙-莫雷实验的结果。

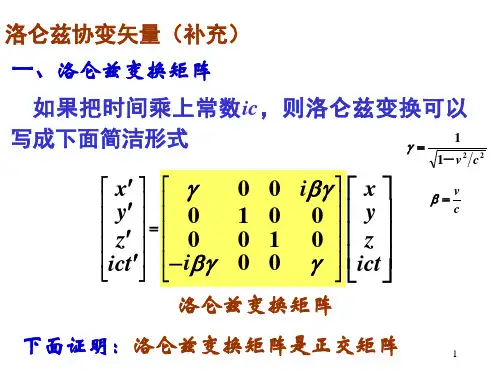
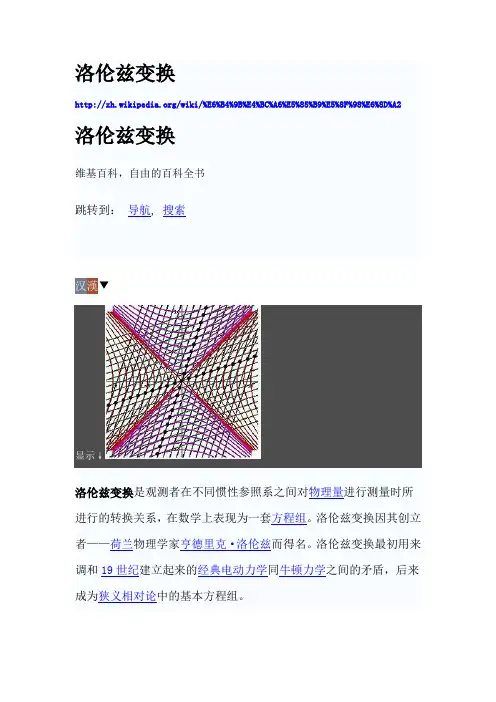
洛伦兹变换/wiki/%E6%B4%9B%E4%BC%A6%E5%85%B9%E5%8F%98%E6%8D%A2 洛伦兹变换维基百科，自由的百科全书跳转到：导航, 搜索汉漢▼显示↓洛伦兹变换是观测者在不同惯性参照系之间对物理量进行测量时所进行的转换关系，在数学上表现为一套方程组。

洛伦兹变换因其创立者——荷兰物理学家亨德里克·洛伦兹而得名。

洛伦兹变换最初用来调和19世纪建立起来的经典电动力学同牛顿力学之间的矛盾，后来成为狭义相对论中的基本方程组。

目录[隐藏]• 1 洛伦兹变换的提出• 2 洛伦兹变换的数学形式• 3 洛伦兹变换的四维形式• 4 洛伦兹变换的推论• 5 洛伦兹变换的几何理解• 6 外部链接沿着快速加速的观察者的世界线来看的时空。

竖直方向表示时间。

水平方向表示距离，虚划线是观察者的时空轨迹（“世界线”）。

图的下四分之一表示观察者可以看到的事件。

上四分之一表示光锥- 将可以看到观察者的事件点。

小点是时空中的任意的事件。

世界线的斜率（从竖直方向的偏离）给出了相对于观察者的速度。

注意看时空的图像随着观察者加速时的变化。

洛伦兹提出洛伦兹变换是基于以太存在的前提的，然而以太被证实是不存在的，根据光速不变原理，相对于任何惯性参照系，光速都具有相同的数值。

爱因斯坦据此提出了狭义相对论。

在狭义相对论中，空间和时间并不相互独立，而是一个统一的四维时空整体，不同惯性参照系之间的变换关系式与洛伦兹变换在数学表达式上是一致的，即：y' = yz' = z其中x、y、z、t分别是惯性坐标系Σ下的坐标和时间，x'、y'、z'、t'分别是惯性坐标系Σ'下的坐标和时间。

v是Σ'坐标系相对于Σ坐标系的运动速度，方向沿x轴。

由狭义相对性原理，只需在上述洛伦兹变换中把v变成-v，x'、y'、z'、t'分别与x、y、z、t互换，就得到洛伦兹变换的反变换式：y = y'z = z'洛伦兹变换是高速运动的宏观物体在不同惯性参照系之间进行坐标和时间变换的基本规律。

一般洛伦兹变换刘婷婷【摘要】在基于爱因斯坦相对性和光速不变性原理的基础上,两种方法推导一般情况下的洛伦兹变换,即1.由特殊洛伦兹变换式推导一般洛伦兹变换式2.闵可夫斯基空间的洛伦兹变换式.并分别运用了洛伦兹变换的矢量形式以及四维时空的“转动”,用变换矩阵的形式来表示一般情况下的洛伦兹变换式.在文章的介绍过程中将坐标转动、变换矩阵以及闵可夫斯基空间的相关内容作了有机的结合,对洛伦兹变换进行了更深一层次的了解.【期刊名称】《应用能源技术》【年(卷),期】2016(000)011【总页数】3页(P9-11)【关键词】特殊洛伦兹变换;一般洛伦兹变换;闵可夫斯基空间;变换矩阵【作者】刘婷婷【作者单位】山西农业大学信息学院,太原030100【正文语种】中文【中图分类】O412.1在证明了爱因斯坦的相对性原理和光速不变原理与伽利略变换有矛盾之后，就需要对人们一直都坚信的空间以及时间概念加以更深入的分析。

经典的洛伦兹变换就是狭义相对论的数学基础[1]。

特殊情况下的洛伦兹变换式[2]，它表示两个惯性系沿x轴做平行运动，如果S和S′系的坐标轴仍保持平行，但在S系中观察S′系的速度是在任意的直线方向上，则两参照系的时空坐标之间不再满足特殊的洛伦兹变换式，下面我们用洛伦兹变换的矢量形式以及四维时空的“转动”推导出普遍的洛伦兹变换式。

由特殊洛伦兹变换得出：从S系到S′系的变换中，垂直于方向上的长度保持不变，而在平行于的方向上，长度的变换则应乘上因子 r，时空的变换则为)，因此，需要将垂直与和平行与的关系分别考虑，即将任一点Q的位矢和都分解到垂直于和平行与的两个分量上。

表示为：用表示方向上的单位矢量，即，则：根据已有结论可得：所以：(5)式和(6)式即为矢量形式的一般洛伦兹变换关系，其分量形式可表示为：因为，则上式相应的变换矩阵为：在闵可夫斯基空间惯性参考系间坐标变换相当于四维空间的转动变换。

在特殊洛伦兹变换下，表示在Z系中所观察的Z′系的速度，表示Z′系中的观察的Z系的速度，如果速度沿任意方向，即并不与z1,z1′轴重合[3]，我们可以通过四维空间的坐标旋转将Z系的z1轴转向方向，旋转后可得惯性系K(o-x1x2x3x4)和Z(o-z1z2z3z4)系之间的变换矩阵为:相应的坐标变换为:然后再将Z′(o-z1′z2′z3′z4′)系的z1′轴转向方向，设旋转后所得的惯性系K′(o-x1′x2′x3′x4′),但x轴沿方向，由于Z和Z′系的坐标轴彼此平行,则在三维空间中，和同向，由此Z′系和K′系间的变换矩阵仍为D。

洛伦兹变换推导过程详细洛伦兹变换是狭义相对论中的一个重要概念，用于描述不同参考系之间的时空坐标转换关系。

它的推导过程可以从狭义相对论的两个基本假设出发，逐步推导出洛伦兹变换的形式。

在狭义相对论中，有两个基本假设：光速不变原理和惯性参考系原理。

光速不变原理指出，光在真空中的传播速度在任何惯性参考系中都是恒定的，即与观察者的运动状态无关。

惯性参考系原理则认为，任何惯性参考系中的物理规律都应该是相同的。

基于这两个假设，可以推导出洛伦兹变换的形式。

假设有两个参考系S和S'，它们之间的相对速度为v。

设S系中某一事件的时空坐标为(x, y, z, t)，在S'系中的时空坐标为(x', y', z', t')。

根据相对性原理，两个参考系之间的坐标变换应该是线性的。

为了推导洛伦兹变换，我们需要考虑两个基本情况：在S系中的事件在S'系中的时间和空间坐标，以及在S'系中的事件在S系中的时间和空间坐标。

根据相对性原理和光速不变原理，可以得到以下两个关系式：1. 在S系中的事件在S'系中的时间坐标：t' = γ(t - vx/c^2)2. 在S系中的事件在S'系中的空间坐标：x' = γ(x - vt)其中，γ是洛伦兹因子，定义为γ = 1 / sqrt(1 - v^2/c^2)，c是光速。

类似地，可以推导出在S'系中的事件在S系中的时间和空间坐标的变换关系：1. 在S'系中的事件在S系中的时间坐标：t = γ(t' + vx'/c^2)2. 在S'系中的事件在S系中的空间坐标：x = γ(x' + vt')这样，就得到了洛伦兹变换的完整形式。

洛伦兹变换的推导过程并不复杂，但需要严密的逻辑推理和数学推导。

通过这个变换，我们可以描述不同参考系之间的时空关系，揭示了狭义相对论中的一些奇特现象，如时间膨胀和长度收缩等。

第三节 洛伦兹变换式教案内容：1. 洛伦兹变换式的推导；2. 狭义相对论的时空观：同时性的相对性、长度的收缩和时间的延缓； 重点难点：狭义相对论时空观的主要结论。

基本要求：1. 了解洛伦兹坐标变换和速度变换的推导；2. 了解狭义相对论中同时性的相对性以及长度收缩和时间延缓概念；3. 理解牛顿力学中的时空观和狭义相对论中的时空观以及两者的差异。

三、洛伦兹坐标变换的推导()()⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧--='='='--='22211c v c vx t t z z y y c v vt x x 或 ()()⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧-'+'='='=-'+'=22211c v c x v t t z z y y c v t v x x据狭义相对论的两个基本假设来推导洛仑兹变换式。

1. 时空坐标间的变换关系作为一条公设，我们认为时间和空间都是均匀的，因此时空坐标间的变换必须是线性的。

对于任意事件P 在S 系和S '系中的时空坐标(x ，y ，z ，t )、(x '，y '，z '，t ')，因S ' 相对于S 以平行于 x 轴的速度v 作匀速运动，显然有y '=y , z '=z 。

在S 系中观察S 系的原点，x =0；在S '系中观察该点，x '=-v t '，即x '+v t '=0。

因此x =x '+v t '。

在任意的一个空间点上，可以设：x =k （x '+v t '），k 是—比例常数。

同样地可得到：x '=k '（x -v t ）= k '（x +(-v )t ）根据相对性原理，惯性系S 系和S '系等价，上面两个等式的形式就应该相同（除正、负号），所以k =k '。