利用三角函数测高(20201010155518)

新北师大版九年级数学下册第一章《利用三角函数测高》优质公开课课件 (2)

测量底部不可以直接到达的物体的高度，如右图
活动报告表：
zxxkw zxxkw
学科网学科网
年月日
这一样个的人人所才受有的学教问育。超
过了自己的智力，
You made my day!
我们，还在路上……
M
x
zxxkw
E
学科网
β
Dα
C
N
B b aA
1、在测点A处安置测倾器，测得此时M的仰角∠MCE=α
2、在测点A与物体之间的B处安置测倾器（A、B与N在一
条直线上），测得此时M的仰角∠MDE=β
3、量出测倾器的高度AC=BD=a，以及测点A，B之间的距
离AB=b
请你用上述数据求出物体的高度MN。
tM anE taM nE b,M NM Ea
C
？
60°
D
B
30°
100
A
议一议
1、到目前为止，你有哪些测量物体高度的方法？
2、如果一个物体的高度已知或容易测量，那么如何测量某测点到该物体的水平距离？
总
结
(1)侧倾器的使用
(2)误差的解决办法---用平均值
zxxkw
学科网
(3)建立数学模型计算两类物体的高度
测量底部可以到达的物体的高度，如左图
2、转动度盘，使度盘的直径对准目标M，记下此时铅垂线所指的读数。
zxxkw
学科网
M
Ｐ
30°
Ｑ
zxxkw
学科网
仰角α
铅垂线所指示的度数
测量底部可以到达的物体的高度
M
zxxkw
E
学科网
α

6 利用三角函数测高

拓展与延伸
如图，测量人员在山脚A处测得山顶B的仰角为45°，沿着倾
角为30°的山坡前进1 000米到达D处，在D处测得山顶B的仰
角为60°，则山高BC大约是（精确到0.1米）（ A ）
A. 1 366.0米
B. 1 482.1米
C. 1 295.9米
D. 1 508.2米
水平线
90° 60° 30°
90°
60°
0°
30°
新课讲解
活动一：测量倾斜角
M
根据刚才测量数据, 你能求出目标M的仰角或俯角吗?说说你的理由.
水平线
同角的余角相等
1
2
4
3
新课讲解
活动二:测量底部可以到达的物体的高度
所谓“底部可以到达”,就是在地面上可以无障碍地直接测得测点与被测物体底部之间的距离. 如图,要测量物体MN的高度,需测量哪些数据？可按下列步骤进行:
新课讲解
知识点1 认识测倾器简单的测倾器由度盘、铅锤和支杆组成。
90 90
P
Q
度盘
0
铅锤
支杆
新课讲解
活动一：测量倾斜角 M
使用测倾器测量倾斜角的步骤如下: 1.把支杆竖直插入地面,使支杆的中心线、铅锤线和度盘的00刻度线重合,这时度盘的顶线PQ在水平位置. 2.转动度盘,使度盘的直径对准目标M,记下此时铅锤线所指的度数.
1.在测点A处安置测倾器,
M
测得M的仰角∠MCE=α.
2.量出测点A到物体底部N的水平距离 E
AN=L.
N
3.量出测倾器的高度AC=a
α
L
a
C A
新课讲解

1.6利用三角函数测高(第2课时)1精品PPT课件

活动三：测量底部不可
M
以到达的物体的高度:所
谓“底部不可以到达”－就
是在地面上不可以直接测得
测点与被测物体之间的距离。
C αD β
E
N
A
B
1在测点A处安置测倾器，测得此时M的仰角∠MCE=α
2在测点A与物体之间的B处安置测倾器，测得此时M的仰角∠MDE=β；
3量出测倾器的高度AC=BD=a，以及测点A,B之间的距离AB=b.根据测量数据,可求出ME物体MEMNb,的MN高 M度E a.
活动一：测量倾斜角 •测量倾斜角可以用测倾器。
----简单的侧倾器由度盘、铅锤和支杆组成
90
9 0
P
Q
度盘
0
铅锤
支杆
使用测倾器测量倾斜角的步骤如下：
P
Q
90 90
0
1、把支杆竖直插入地面，使支架的中心线、铅垂线和度盘的0°刻度线重合，这时度盘的顶线PQ在水平位置。
90 90
M
30°
0
2、转动转盘，使度盘的直径对准目标M，记下此时铅垂线所指的度数。
得，D'E AE
在Rt△ADE中，由 tan 30 AE 得，DE 3AE
DE
所以50= 3AE A，E则 AE 50 68.3
3 1
D
所以,物体高度为AB=68.3+1.2=69.5米。
C
A
D´
E
C´
B
写在最后
经常不断地学习,你就什么都知道。你知道得越多,你就越有力量 Study Constantly, And You Will Know Everything. The
第一章直角三角形的边角关系

《利用三角函数测高》课件

ME ME b, MN ME a tan tan
下表是小亮所填实习报告的部分内容: 课题在平面上测量地王大厦的高AB
A
测量示意图 E
α
F
β
∠α
30° 16’ 29° 44’
G
B
C
测量项目测得数据第一次第二次平均值
D
∠β
44° 35’ 45° 25’
CD的长 60.11m 59.89m
活动报告
课题测量示意图测量项目第一次第二次平均值
测得数据
计算过程活动感受负责人及参加人员计算者和复核者指导教师审核意见
备注
如图，某中学在主楼的顶部和大门的上方之间挂一些彩旗．经测量，得到大门的高度是５m，大门距主楼的距离是 30m，在大门处测得主楼顶部的仰角是30°，而当时侧倾器离地面1.4m,求学校主楼的高度 (精确到0.01m)
M
解：如图，作EM垂直CD于M点,根据题意，可知 EB=1.4m，∠DEM=30°,BC=EM=30 m, CM=BE=1.4m 在Rt△DEM中，DM=EMtan30°≈30×0.577 =17.32(m) CD=DM+CM=17.32+1.4=18.72(m)
M
30°
90 0 90
2、转动转盘，使度盘的直径对准目标M，记下此时铅垂线所指的度数。
测量底部可以直接到
达的物体的高度:
M
C
α
E
A N 1、在测点A安置测倾器，测得M的仰角∠MCE=α ； 2、量出测点A到物体底部N的水平距离AN=l； 3、量出测倾器的高度AC=a，可求出MN的高度。
MN=Mபைடு நூலகம்+EN=l· tanα +a

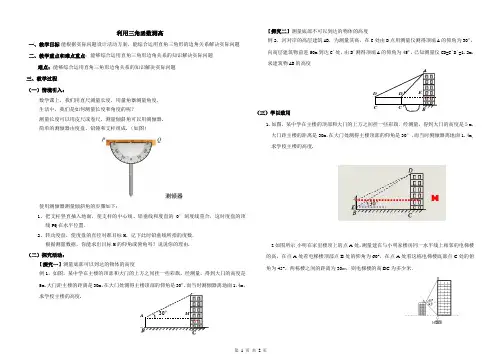
利用三角函数测高度

利用三角函数测高一、教学目标能根据实际问题设计活动方案，能综合运用直角三角形的边角关系解决实际问题二、教学重点和难点重点：能够综合运用直角三角形边角关系的知识解决实际问题难点：能够综合运用直角三角形边角关系的知识解决实际问题三、教学过程（一）情境引入：数学课上，我们用直尺测量长度，用量角器测量角度. 生活中，我们是如何测量长度和角度的呢？测量长度可以用皮尺或卷尺，测量倾斜角可以用测倾器. 简单的测倾器由度盘、铅锤和支杆组成.（如图）测倾器使用测倾器测量倾斜角的步骤如下：1、把支杆竖直插入地面，使支杆的中心线、铅垂线和度盘的0°刻度线重合，这时度盘的顶线PQ 在水平位置．2、转动度盘，使度盘的直径对准目标M ，记下此时铅垂线所指的度数．根据测量数据，你能求出目标M 的仰角或俯角吗？说说你的理由. （二）探究活动：【探究一】测量底部可以到达的物体的高度例1，如图，某中学在主楼的顶部和大门的上方之间挂一些彩旗，经测量，得到大门的高度是5m ，大门距主楼的距离是30m ，在大门处测得主楼顶部的仰角是30º，而当时测倾器离地面1.4m ，求学校主楼的高度.【探究二】测量底部不可以到达的物体的高度例2，河对岸的高层建筑AB ，为测量其高，在C 处由D 点用测量仪测得顶端A 的仰角为30º，向高层建筑物前进50m 到达C ´处，由D ´测得顶端A 的仰角为45º，已知测量仪CD=C ´D ´=1.2m ，求建筑物AB 的高度（三）学以致用1.如图，某中学在主楼的顶部和大门的上方之间挂一些彩旗．经测量，得到大门的高度是５m ，大门距主楼的距离是30m ，在大门处测得主楼顶部的仰角是30°，而当时侧倾器离地面1.4m,求学校主楼的高度.2.如图所示,小明在家里楼顶上的点A 处，测量建在与小明家楼房同一水平线上相邻的电梯楼的高，在点A 处看电梯楼顶部点B 处的仰角为60°，在点A 处看这栋电梯楼底部点C 处的俯角为45°，两栋楼之间的距离为30m ，则电梯楼的高BC 为多少米．MAM30º AD BCE C ´D ´3.如图，如图，有一段斜坡BC 长为10米，坡角12CBD ︒∠=，为方便残疾人的轮椅车通行，现准备把坡角降为5°．（1）求坡高CD ；（2）求斜坡新起点A 与原起点B 的距离（精确到0.1米）．（参考数据：sin5°≈0.1 ，cos5°≈0.9 ， tan5°≈ 0.1 ， Sin12°≈0.2 ，cos12°≈0.8 ，tan12°≈0.2 ）（四）拓展提升1.我市某乡镇学校教学楼后面靠近一座山坡，坡面上是一块平地，如图所示．BC AD ∥，斜坡40AB =米，坡角60BAD ∠=，为防夏季因瀑雨引发山体滑坡，保障安全，学校决定对山坡进行改造．经地质人员勘测，当坡角不超过45时，可确保山体不滑坡，改造时保持坡脚A 不动，从坡顶B 沿BC 削进到E 处，问BE 至少是多少米（结果保留根号）？2.如图是某货站传送货物的平面示意图. 为了提高传送过程的安全性，工人师傅欲减小传送带与地面的夹角，使其由45°改为30°. 已知原传送带AB 长为4米. （1）求新传送带AC 的长度；（2）如果需要在货物着地点C 的左侧留出2米的通道，试判断距离B 点4米的货物MNQP 是否需要挪走，并说明理由．(说明：⑴⑵的计算结果精确到0.1米) （参考数据：2≈1.41，3≈1.73，5≈2.24，6≈2.45)3.如图，某货船以20海里/时的速度将一批货物由A 处运往正西方向的B 处，经16小时到达，到达后必须立即卸货。

利用三角函数测高北师大版九年级数学下册

风板FG与EF夹角成136°，风沿FG方向吹出，为了让空调风不直接吹到
床上，空调安装的高度(BC的长)至少为多少？(精确到个位)(参考数据：
cos46°≈0.69，tan46°≈1.04，sin46°≈0.72)
【分析】连接AF,作FH⊥AD构造直角三角形运用三
角函数解出FH,再将床高加上即可求出EC的值．
解这个方程得：x≈45.1，
经检验：x≈45.1符合题意．
∴灯塔的高CF＝55.1≈55（m）
答：灯塔的高为55米．
课堂总结
测倾器的认识及使用
利用三角函
数测高
测量底部可以到达的物体的
高度（一次测量仰角）
测量底部不可以到达的物体
的高度（两次测量仰角）
利用解三角
形的知识，
求出物体的
高度
直角三角形，将仰角或俯角置于这个三角形中，选择正确的三
角函数，并借助计算器求出要求的量．
活动三:测量底部不可以到达的物体的高度．
所谓“底部不可以到达”，就是在地面上不能直接测得
测点与被测物体的底部之间的距离．
如图1-17，要测量物体MN的高度，可按下列步骤进行:
图1-17
1．在测点A处安置测倾器，测得此时M的仰角∠MCE=α.
【详解】当A、F在一条直线时,就正好不会吹到床上,
连接AF,过点F作FH⊥AD,
∵AD=200,HD=20,
∴AH=180,
∵∠EFA=136°,
∴∠FAD=46°,
∴FH=AH·tan46°=180×1.04=187.2
∴ED=FH=187.2,
∴EC=187.2+50=237.2≈237．
故答案为237．
所谓“底部可以到达”，就是在地面上可以无障碍

利用三角函数测高优质课件

量出测倾器的高度AC=a，可求出MN的高度。
MN=ME+EN=L·tanα+α
理论实践如图，为测量一棵与地面垂直的树OA的高度，在距离树的底端30米的B处，测得树顶A的仰角
∠ABO为α，则树OA的高度为( C )
A.tanα米 B.30sinα米 C.30tanα米 D.30cosα米
二．实践活动（二）
一.实践活动（一） M
C 34
E
1.6米
19米
A
N
ME 19 tan 34（ m）
MN ME EN
MN (19 tan 34 1.6) 14.4（2 m）
测量底部可以直接到达的
M
物体的高度
在观测点A安置测倾器，测
得M的仰角∠MCE=α
Cα
E
a
L
量出观测点A到物体底部N
A
N
的水平距离AN=L
理论实践
如图所示，河对岸有古塔AB，小敏在C处测得塔顶
A的仰角为α，向塔走s米到达D，在D处测得塔顶A S tan tan
的仰角为β，则塔高是 tan tan 米.
小组成员的自我反思
课堂小结
1.到目前为止，你还有哪些方法可以测得国旗杆高度和居民楼高度？
2.你还有哪些收获，想跟大家分享？
1. 分组制作简单的测倾器.
2.选择一个底部可以到达的物体,测量它的高度并撰写一份活动报告,阐明活动课题、测量示意图、测得数据和计算过程等.
3.选择一个底部不可以到达的物体,测量它的高度并撰写一份活动报告,阐明活动课题、测量示意图、测得数据和计算过程等.
课题
测量示意图
测得数据
测量项目第一次第二次

6利用三角函数测高

C′
B′
x ta 6 n 0 x ta 3 n 0 50 D
C
B
x 5 0 2 53 4 3 .3 (m ) ta n 6 0 ta n 3 0
x 4 3 .3 1 .5 4 4 .8 4 5 ( m )
解：（1）由题意，AC＝AB＝610（米）；（2）DE＝AC＝610（米），在Rt△BDE中，tan∠BDE＝ B E ，
∠DEM=30°,BC=EM=30 m,
M
CM=BE=1.4m
在Rt△DEM中， DM=EMtan30°≈30×0.577 =17.32(m)， CD=DM+CM=17.32+1.4=18.72(m).
三测量底部不可以到达的物体的高度
问题1：在黄浦江的另一端，你能否测量东方明珠的高度呢？
在现实生活中，我们不可以直接从测点到达被测点的脚
Eα F β
G
B CD
30° 45°
60m
解：由表格中数据，得α=30° ，β=45° ,
QtanAG,tanAG,
EG
FG
EG AG AG 3AG,
tan tan30
FG AG AG AG,
tan tan45
CDEF EGFG( 31)AG,
A G C D6 03 0 (3 1 )(m ), 3 1 3 1
DE
4.小明家所在居民楼的对面有一座大厦AB，AB＝ 80米．为测量居民楼与这座大厦之间的距离，小明从自己家的窗户C处测得大厦顶部A的仰角为 37°，大厦底部B的俯角为48°．求小明家所在居民楼与大厦的距离CD的长度．（结果保留整数）
（参考数据：s i n 3 7 o 3 ， t a n 3 7 o 3 ， s i n 4 8 o 7 ， t a n 4 8 o 1 1 ）

1.6 利用三角函数测高

一、测量底部可以到达的物体的高度
所谓“底部可以到达”－－－就是在地面上可以无障碍地直接测得测点与被测物体的底部之间的距离.
如图，要测量物体MN的高度，可按下列步骤进行：
M
αC
E
N
A
活动一：测量底部可以到达的物体的高度
交流研讨，确定方案：
1、在A处测得物体顶部M的仰角∠MCE＝
l 2、量出A到物体底部N的水平距离AN＝
1、把支架竖直插入地面，使支架的中心线、铅锤线和度盘的0°刻度线重合，这时度盘的顶线PQ在水平位置。
M
3Ｐ0°
Ｑ
9 0
9 0
0
2、转动度盘，使度盘的直径对准目标M，记下此时铅垂线所指的读数。
M
Ｐ
30°
Ｑ
测量物体高度的原理
1、回忆所学测量物体高的方法 2、如何根据“三角函数”测高
类型一：物体底部可到达类型二：物体底部不可到达
第一章直角三角形的边角关系
1.6 利用三角函数测高
活动一：测量倾斜角
测量长度可以用皮尺或卷尺，测量倾斜角可以用测倾器。简单的测倾器由度盘、铅锤和支杆组成。
如何测量倾斜角
•测量倾斜角可以用测倾器。 ----简单的侧倾器由度盘、铅锤和支
杆组成
90
9 0
P
Q
度盘
0
铅锤
支杆
活动：测量倾斜角
使用测倾器测量倾斜角的步骤如下： 1、把支杆竖直插入地面，使支杆的中心线、铅垂线和度盘的0°刻度线重合，这时度盘的顶线PQ在水平位置． 2、转动度盘，使度盘的直径对准目标M，记下此时铅垂线所指的度数．
如图，要测量物体MN的高度，可按下列步骤进行：
DC

专题1-6 利用三角函数测高-2022-2023学年九年级数学下册教材配套教学课件(北师大版)

CF=BE,EF=BC,∠A=α,∠B=β.
BE 5.8m,
BE
1 CF
1

,

,
AE 1.6 DF 2.5
B
A
i=1:1.6
α
9.8
C
β
i=1:2.5 5.8
D
F
E
∴AE=1.6×5.8=9.28(m),DF=2.5×5.8=14.5(m).
∴AD=AE+EF+DF=9.28+9.8+14.5≈33.6(m).
AB=b.根据测量数据,可求出物体MN的高度.
当堂练习
1．如图，窗子高AB=m米，窗子外面上方0.2米的点C处安装
水平遮阳板CD=1米，当太阳光线与水平线成α=60°角时，光
线刚好不能直接射人室内，则m的值是（
）
A．m= +0.8
C．m= -0.2
B．m= +0.2
D．m= -0.8
【答案】C
问题1：在黄浦江的另一端，你能否测量东方明珠的高度呢？
在现实生活中，我们不可以直接从被测点到达被测点
的脚下，这时我们能利用两次测量仰角（图中α和β），
再结合解三角形的知识来求出东方明珠的高度.
所谓“底部不可以到达”，就是
在地面上不能直接测得测点与被测
物体的底部之间的距离，
如图中的AN或BN的长度.
Cα D β
在Rt△DEG中，∠EDG＝45°，
∴EG＝DE＝10m．∠EGD＝45°
设CH＝xm，
在Rt△CGH中，∠CGH=∠EGD＝45°，
∴GH＝xm
在Rt△CBH中，∠CBH＝28°，

∴tan∠CBH＝，