多边形的面积组合图形

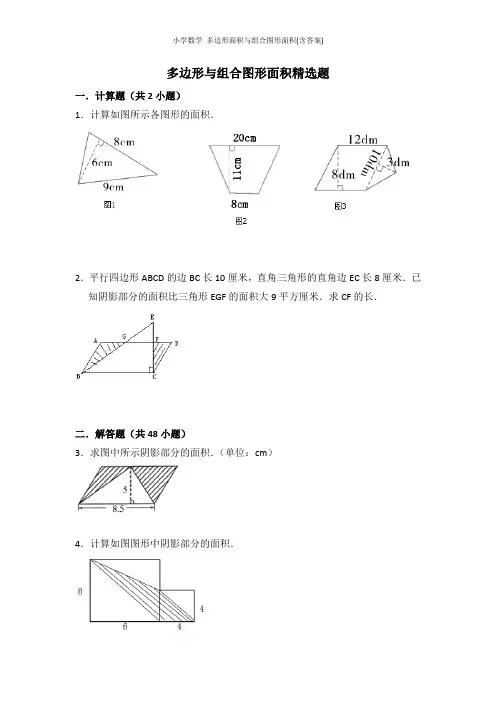
多边形与组合图形面积精选题一．计算题（共2小题）1．计算如图所示各图形的面积．2．平行四边形ABCD的边BC长10厘米，直角三角形的直角边EC长8厘米．已知阴影部分的面积比三角形EGF的面积大9平方厘米．求CF的长．二．解答题（共48小题）3．求图中所示阴影部分的面积．（单位：cm）4．计算如图图形中阴影部分的面积．5．如图所示是学校生态园的平面图，你能算出生态园的面积吗？（单位：m）6．计算下面图形的面积．7．图形由两个正方形组成，求阴影部分的面积．（单位：cm）8．计算阴影部分的面积．9．在如图所示中剪出一个最大的长方形，画出来并求出剩余部分的面积．10．求如图平面图形的面积．11．李大爷家有一块菜地（如图所示）你能用巧妙的方法算出菜地的周长和面积吗？12．一张长8厘米，宽4厘米的长方形纸，从下边的中点和右上角顶点连线一条线段，沿这条线段剪去一个角（如图所示），剩下的面积是多少？13．用篱笆围一块菜地，如图的梯形，一边利用房屋的墙壁，已知梯形上、下底的比为3：5，篱笆长40米，求菜地面积．14．把一个大平行四边形分成3块，（如图）已知图形阴影部分是平行四边形，面积是12平方米，求三角形和梯形的面积各是多少？15．如图，三角形ABC的面积是56平方米，BD=DC，DE垂直于AC，AC=14米．求图中阴影部分的面积．16．李大伯一边利用房屋干墙壁，另三边用篱笆围成一个梯形养鸡场地（如图）．篱笆总长是36米．求这个养鸡场的面积是多少？17．求下列图形中阴影部分的面积．18．看图计算如图图形的面积．19．认真观察，巧计算．（用两种方法计算组合图形的面积）20．一块水稻田的形状如下图．如果按照平均每穴30平方分米插秧，大约要插多少穴？21．求组合图形的面积．（1）图1的面积是：；（2）图2的面积是：．22．如图，已知四条线段的长分别是：AB=2厘米，CE=6厘米，CD=5厘米，AF=4厘米，并且有两个直角．求四边形ABCD的面积．23．如图，长方形里有四个三角形，已知其中的三角形的面积，求三角形ADE 的面积．24．（如图）三角形ABC的周长为80厘米，形内有一点P到三角形三条边的距离都是8厘米，求三角形ABC的面积．25．求如图图形的面积．26．我会计算阴影部分的面积．27．如图：ABCE是一个梯形，其中ABCD是长8厘米，宽7厘米的长方形，AF 长是4厘米，求阴影部分的面积？28．如图是由两个完全一样的直角三角形叠在一起而成的，求阴影部分的面积．（单位：厘米）29．计算下列图形的面积．（单位：厘米）30．如图所示，长方形的ABCD面积被线段AE，AF分成三等份，且三角形AEF 的面积是35平方厘米，求长方形的面积．31．图中长方形的面积是432平方厘米，求阴影部分的面积．32．如图所示，已知正方形和三角形有一部分重叠，三角形乙比三角形甲面积大7平方厘米，则X=厘米．33．用篱笆围成一个养鸡场（如图所示），一面靠墙，篱笆总长90米，下底长度是上底长度的3倍．求这个养鸡场的面积．34．如图正方形ABCD的边长是4分米，长方形EFGD的长GD是5分米，求DE 的长．35．已知如图大正方形的边长是5厘米，小正方形的边长是3厘米，求阴影部分的面积．36．如图所示，长方形ABCD的面积是180平方厘米，CD长15厘米，ED长17厘米，求三角形ACE的面积．37．图中的两个正方形的边长分别是10厘米和6厘米，求阴影部分的面积．38．如图ABCD是梯形，∠A=∠B=90°，AB=12cm，BC=6cm，甲、乙两阴影面积之差为24cm2，求ABCD的面积．39．有一块如图形状的菜田，算一算：①占地多少公顷？所需数据在图中选择．（单位：m）②如果每公顷需要施化肥50千克，这块地一共要施肥多少千克？40．你能求出下列图形的周长吗？41．求组合图形的面积．（单位：米）42．如图，一个梯形的上底是5厘米，下底是8厘米．三角形的高是4厘米，并把三角形分为面积相等的甲乙两部分，求阴影部分的面积．43．求如图的面积或阴影面积：44．如图，是大小两个正方形组成的图形，大正方形边长是8厘米，小正方形边长为6厘米，求阴影部分的面积．45．如图，正方形ABCD的边AB、BC分别在三角形BEF的BE、BF边上，顶点D 在EF边上，点D把EF分成两段，DE=12米，DF=15米，求两个阴影三角形的面积和．46．在长方形ABCD中，AD=15厘米，AB=8厘米，四边形EFGO的面积是9平方厘米，阴影部分的面积是多少平方厘米？47．如图是由两个平行四边形组成的，这个图形的面积是多少？48．如图，四边形ACEH是梯形，ACEG是平行四边形，ABGH是正方形，CDFG 是长方形．已知，AC=8厘米，HE=13厘米，求阴影部分的面积．49．图中长方形的面积是180平方厘米，S1的面是45平方厘米，S2的面积是60平方厘米．求阴影部分的面积．50．有一块铁皮，形状如图所示．如要油饰这块铁皮的一面，每平方米用油漆0.6千克，刷完这块铁皮需要多少千克油漆？多边形与组合图形面积精选题参考答案与试题解析一．计算题（共2小题）1．【解答】解：（1）8×6÷2=24（平方厘米）答：三角形的面积是24平方厘米．（2）（8+20）×11÷2=28×11÷2=154（平方厘米）答：梯形的面积是154平方厘米．（3）12×8+10×3÷2=96+15=111（平方分米）答：这个图形的面积是111平方分米．2．【解答】解：设EF长为x厘米，则CF就是8﹣x厘米，根据题干分析可得方程：10×（8﹣x）=10×8÷2+9 80﹣10x=49 10x=31 x=3.18﹣3.1=4.9（厘米）；答：CF长为4.9厘米．二．解答题（共48小题）3．【解答】解：8.5×5﹣8.5×5÷2=42.5﹣21.25=21.25（cm2），答：阴影部分的面积为21.25cm2．4．【解答】解：6×6+4×4﹣6×6÷2﹣4×4÷2﹣6×（6﹣4）÷2=36+16﹣18﹣8﹣6=20（平方厘米）答：阴影部分的面积是20平方厘米．5．【解答】解：20﹣12=8（米）16﹣10=6（米）12×16+8×6÷2=192+24216（平方米）答：生态园的面积是216平方米．6．【解答】解：15×4=60（平方米），答：它的面积是60平方米．7．【解答】解：（10+8）×10÷2=18×5=90（平方厘米）答：阴影部分的面积是90平方厘米．8．【解答】解：30×28÷2=30×14=420（平方厘米）答：阴影部分的面积是420平方厘米．9．【解答】解：如图所示，（12﹣6）×（10﹣5）÷2=6×5÷2=15（平方厘米）答：剩余部分的面积是15平方厘米．10．【解答】解：（1）15×30=450（平方厘米）答：平行四边形的面积是450平方厘米．（2）5×2÷2+5×3=5+15=20（平方米）答：这个图形的面积是20平方米．11．【解答】解：周长是：（17+8+23）×2=48×2=96（米）面积是：（17+8）×23﹣（23﹣8）×17=25×23﹣15×17=575﹣255=320（平方米）答：周长是96米，面积是329平方米．12．【解答】解：（8+8÷2）×4÷2=（8+4）×4÷2=12×4÷2=24（平方厘米），答：剩下的面积为24平方厘米．13．【解答】解：如图：5﹣3=240×=8（米）40×=20（米）40×=12（米）（12+20）×8÷2=32×8÷2=128（平方米）答：菜地面积是128平方米．14．【解答】解：因为大平行四边形的对边平行且相等，所以阴影部分的高=12÷3=4（米），所以三角形的面积=×3×4=6（平方厘米），梯形的面积=（3+6）×4=18（平方厘米）．答：三角形的面积是6平方厘米，梯形的面积是18平方厘米．15．【解答】解：因为BD=DC，所以三角形ABD和三角形ADC的面积相等，因为三角形ABC的面积是56平方米，所以图中阴影部分的面积为：56÷2=28（平方米）答：阴影部分的面积是28平方米．16．【解答】解：（36﹣10）×10÷2=26×10÷2=130（平方米）答：这个养鸡场的面积是130平方米．17．【解答】解：（2+9+2）×（2+4+2）+2×2×4=13×8﹣16=104﹣16=88（平方厘米）答：阴影部分的面积是88平方厘米．18．【解答】解：（1）8×3=24（平方分米）答：图形的面积是24平方（2）25×14÷2=25×7=175（平方米）答：图形的面积是175960平方厘米．（3）分米．（26+34）×32÷2=60×32÷2=960（平方分米）答：图形的面积是960平方分米．（4）26×20+（26+30）×5÷2=520+56×5÷2=520+140=660（平方厘米）答：图形的面积是60平方厘米．（5）6×7+（8﹣6）×（7﹣2.5）÷2=42+2×4.5÷2=42+4.5=46.5（平方厘米）答：图形的面积是46.5平方厘米．19．【解答】解：（1）如图所示，，4×10+（9+10）×（5﹣4）÷2=40+9.5=49.5（平方厘米）（2）如图所示，，5×9+（4+5）×（10﹣9）÷2=45+4.5=49.5（平方厘米）答：组合图形的面积是49.5平方厘米．20．【解答】解：8×11÷2+（11+22）×10÷2=44+165=209（平方分米）209÷30=6（穴）…29（平方分米）6+1=7（穴）答：大约要插7穴．21．【解答】解：（1）24×8+10×24÷2=192+120=312（平方米）答：组合图形的面积为312平方米．（2）12×6+（12+6）×6÷2=72+18×3=72+54=126（平方米）答：组合图形的面积为126平方米．故答案为：312，126．22．【解答】解：连接AC，就变成ADC和ABC两个三角形，如图：三角形ABC 已知底AB=2（厘米）高就是CE=6（厘米）那么三角形ABC面积就是2×6÷2=6（平方厘米）三角形ADC已知底DC=5（厘米）高就是AF=4（厘米）三角形ADC 面积是5×4÷2=10（平方厘米）ABCD面积是10+6=16（平方厘米）答：四边形ABCD的面积16平方厘米．23．【解答】解：如图：S △ABE面积+S△DEC面积=（AB×EF）÷2+（DC×EG）÷2，因为AB=DC，两个三角形高的和等于AD，所以，S△ABE面积+S△DEC面积=AB×AD÷2=长方形面积的一半；同理，另两个三角形面积的和也是长方形面积的一半，即S△ABE面积+S△EDC面积=S△ADE面积+S△BCE面积，即S△=37+29﹣41=25．24．【解答】解：如图：S△ABC =S△APB+S△APC+S△BPC=AB×BP÷2+AC×PE÷2+BC×PD÷2=PD×（AB+AC+BC）=×8×80=320（平方厘米）答：三角形ABC的面积是320平方厘米．25．【解答】解：（1）14×12÷2=168÷2=84（平方厘米），答：面积是84平方厘米；（2）（12+18）×16÷2=30×16÷2=240（平方米），答：面积是240平方米．26．【解答】解：15×9﹣6×6=135﹣36=99（平方分米）答：阴影部分的面积是99平方分米．27．【解答】解：8×7÷2﹣8×4÷2=28﹣16=12（cm2）答：阴影部分的面积是12平方厘米．28．【解答】解：S=[（8﹣3）+8]×5÷2=65÷2=32.5（平方厘米）；答：阴影部分的面阴影积是32.5平方厘米．29．【解答】解：（1）12×8﹣×（12﹣4﹣4）×3，=96﹣6，=90（平方厘米）；（2）12×8+×10×（12﹣5），=96+35，=131（平方厘米）．30．【解答】解：根据以上分析知：S△EFC=EC×CF=×BC×CD=BC ×CD=×ABCD的面积，四边形AECF的面积=×ABCD的面积，设长方形ABCD 的面积为S，根据题意得：（﹣）×S=35 S=35，S=126．答：这个长方形有面积是126平方厘米．31．【解答】解：432÷36×6÷2=12×6÷2=72÷2=36（平方厘米）答：阴影部分的面积是36平方厘米．32．【解答】解：三角形乙的面积比三角形甲的面积大7平方厘米，根据图形可得：三角形ABE的面积比正方形ABCD 的面积大7平方厘米，所以三角形ABE的面积为：7×7+7=49+7=56（平方厘米），又因为AB=7厘米，所以BE的长度是：56×2÷7=16（厘米），所以CE的长度为：16﹣7=9（厘米），即X=9厘米．答：X的长度是9厘米．故答案为：9．33．【解答】解：3﹣1=290÷（3+3）=15（米）下底：15×3=45（米）高：15×2=30（米）面积：（15+45）×30÷2=30×30=900（平方米）答：这个养鸡场的面积是900平方米．34．【解答】解：4×4÷2=8（平方分米），8×2÷5=3.2（分米）．答：DE的长是3.2分米．35．【解答】解：（5+3）×3÷2+5×5÷2﹣3×（3+5）÷2，=8×3÷2+5×5÷2﹣3×8÷2，=12+12.5﹣12，=12.5（平方厘米）．答：阴影部分的面积是12.5平方厘米．36．【解答】解：连接ED，AD=BC=180÷15=12（厘米），AE2=172﹣122=145（平方厘米），AE=，三角形ACE的面积是：×12÷2，=6（平方厘米）；答：三角形ACE的面积是6平方厘米．37．【解答】解：大三角形面积：10×（10+6）÷2=80（平方厘米），小三角形面积：10×10÷2=50（平方厘米），阴影部分三角形面积：80﹣50=30（平方厘米）．答：阴影部分的面积是30平方厘米．38．【解答】解：12×AD÷2﹣12×6÷2=24，6AD﹣36=24，6AD=60，AD=10；梯形的面积为：（6+10）×12÷2，=16×12÷2，=96（平方厘米）；答：ABCD的面积是96平方厘米．39．【解答】解：①×（75+125）×40+×125×48=4000+3000=7000（平方米），7000平方米=0.7公顷；答：占地0.7公顷．②0.7×50=35（千克）；答：这块地一共要施肥35千克．40．【解答】解：（1）4+3+3=10（2）（5+3）×2=16（3）4+2+3+5+2=16．41．【解答】解：5×4÷2+7×5+（5+12）×3÷2=5×4÷2+7×5+17×3÷2=10+35+25.5=70.5（平方米）答：面积是70.5平方米．42．【解答】解：[5﹣（8﹣5）+5]×4÷2，=[5﹣3+5]×4÷2，=[2+5]×4÷2，=7×4÷2，=28÷2，=14（平方厘米）；答：阴影部分的面积为14平方厘米．43．【解答】解：（1）（15+20）×25÷2+12×20÷2=437.5+120=557.5答；图形的面积是557.5．（2）12×8﹣4×8÷2=96﹣16=80答：阴影部分的面积是80．44．【解答】解：阴影部分的面积：6×6÷2=36÷2=18（平方厘米）答：阴影部分的面积是18平方厘米．45．【解答】解：据分析解答如下：12×15÷2=90（平方米）；答：两个阴影三角形的面积和是90平方米．46．【解答】解：15×8﹣15×8÷2+9，=120﹣60+9，=69（平方厘米）．答：阴影部分的面积是69平方厘米．47．【解答】解：3×7.5=22.5（平方厘米）．答：这个图形的面积是22.5平方厘米．48．【解答】解：因为ACEG是平行四边形，所以AC=GE=8厘米又已知HE=13厘米，所以HG=13﹣8=5（厘米）故GB=5厘米所以红色三角形的面积是：8×5÷2=20（平方厘米）即阴影部分的面积是20平方厘米．答：阴影部分的面积是20平方厘米．49．【解答】解：连接BD，则S△BCD=180÷2=90（平方厘米），S△BDF=90﹣60=30（平方厘米），所以BF：BC：=1：3；同理，BE：AB=1：2，因此S△BEF=BE×BF，=×BC×AB，=BC×AB，=×180，=15（平方厘米）；阴影部分的面积：180﹣60﹣45﹣15，=180﹣120，=60（平方厘米）．答：阴影部分的面积是60平方厘米．50．【解答】解：（3×1.2÷2+5×2.4）×0.6，=（1.8+12）×0.6，=13.8×0.6，=8.28（千克）；答：刷完这块铁皮需要8.28千克油漆．。

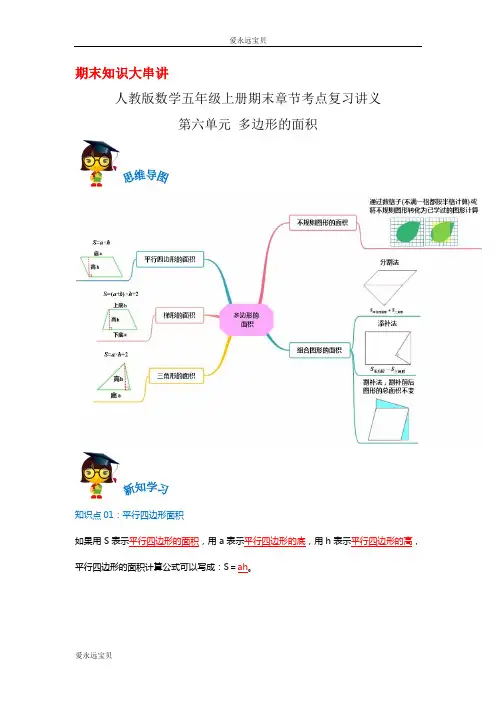
期末知识大串讲人教版数学五年级上册期末章节考点复习讲义第六单元多边形的面积知识点01：平行四边形面积如果用S表示平行四边形的面积，用a表示平行四边形的底，用h表示平行四边形的高，平行四边形的面积计算公式可以写成：S＝ah。

知识点02：三角形的面积两个完全相同的三角形可拼成平行四边形，三角形的面积是拼成的平行四边形面积的一半。

三角形的面积＝底×高÷2，用字母表示为：S ＝ah ÷2 知识点03：梯形的面积梯形的面积=（上底+下底）×高÷2，用字母表示为：S=（a+b ）h ÷2知识点04：组合图形的面积1. 组合图形面积的求法：把组合图形分割或者拼凑成已学过的简单图形,再算这些简单图形的面积的和,就是组合图形的面积。

2.不规则图形面积的求法：数方格的方法进行估算；把不规则的图形转化为学过的图形进行估算。

考点01：平行四边形的面积1．（2021秋•和平区期末）平行四边形的相邻边分别长10cm 和8cm ，其中一条边上的高是9cm ，那么另外一条边上的高是（ ）cm 。

A ．12B ．11.25C ．7.2D ．3【思路引导】根据直角三角形的特征，在直角三角形中斜边最长，由此可知，高9厘米上底下底b对应的底边是8厘米，根据平行四边形的面积公式：S＝ah，那么h＝S÷a，把数据代入公式解答。

【完整解答】解：8×9÷10＝72÷10＝7.2（厘米）答：另外一条边上的高是7.2厘米。

故选：C。

2．（2021秋•河南县期末）小明将一些数学本摞成一个长方体，它的前面是一个长方形，再将它均匀地斜放，这时前面变成了一个近似的平行四边形，比较这两摞数学本的前面，（）相同。

A．形状B．面积C．周长D．周长和面【思路引导】根据题意可知，将这摞书的前面由长方形变成平行四边形，平行四边形的底等于长方形的长，平行四边形的高等于长方形的宽，虽然前面的形状变了，但是面积不变。

组合图形的面积课题：组合图形的面积教学目标：1、了解并掌握什么是组合图形2、了解并掌握什么是分割法、添补法、割补法3、会灵活采用分割法、添补法、割补法来解决生活中组合图形的面积4、再次感受转化思想在数学中的重要意义教学重点：根据图形的特点选择恰当的方法教学难点：如何根据图形的特点选择恰当的方法教学过程：一、复习旧知师：前面我们已经学过一些简单图形面积的计算方法，下面我们就先来一起回忆一下这些图形面积的计算方法。

师：长方形的面积等于……生：长×宽师：正方形的面积等于……生：边长×边长师：平行四边形的面积等于……生：底×高师：三角形的面积等于……生：（底×高)÷2师：梯形的面积等于……生：（上底+下底)×高÷2师（过渡语）：看来同学们对前面的知识掌握得还不错，其实在我们的生活中有一些是由这些简单图形组合而成的，就像他们一样……（播放幻灯片）像这样由两个或两个以上简单图形组合而成的图形叫————组合图形——又叫———不规则图形。

师：（揭示课题）这些组合图形的面积应该怎么计算呢？今天我们就一起来学习——组合图形的面积二、探索新知师：请同学们先题目读一遍、再读一遍；师：同学们看一看小华家的这块地板是一个什么图形；生：组合图形（不规则图形）师：那应该怎么办呢？生：把不规则图形转化成规则的图形来算……师：下面就请同学们想办法帮小华算一算它到底需要买多大面积的地板呢？……小组合作、交流、做好后每组选一名同学汇报 ……可能出现的方法有：师：这里有这么多方法，你们说小华会先择哪一种方法呢？为什么？生：因为这种方法好算师：也就是说我们在算组合图形的面积的时候要根据图形的特点，选择便于我们好计算，好理解的方法。

师：下面我想请同学对黑板上的这几种方法分分类，你会怎么分呢？分成几类？生：三类师：为什么分三类？又是哪三类？生：学生说出每一类的共同点？共同说出这三类方法的名称………………师（小结）：这就是我们今天学习的组合图形面积计算的方法，在我们的实际生活中到底选哪一种方法呢？就要根据实际情况来定………………哪种方法好算就选择哪种方法。

人教版五年级数学上册第六单元多边形的面积第4课时组合图形的面积教学目标】1．明确组合图形的意义，掌握用分解法或添补法求组合图形的面积。

2．能根据各种组合图形的条件，有效地选择计算方法并进行正确解答。

3．渗透“转化”的数学思想，提高学生运用新知识解决实际问题的能力，在自主探索活动中培养他们的创新精神。

【教学重、难点】重点：在探索活动中，理解组合图形面积计算的多种方法，会找出计算每个简单图形的面积所需的条件。

难点：选择有效的计算方法解决实际问题。

【教学准备】七巧板、课件、简单图形学具，少先队中队旗实物。

【教学过程】一、七巧板拼图游戏，初步感知组合图形师：课前请大家用一些我们已学的简单图形的小纸板做一套七巧板。

都做好了吗？都有些什么图形？(预设)有正方形、长方形、平行四边形、三角形、梯形。

师：怎样计算它们的面积？指名让学生说出正方形、长方形、平行四边形、三角形、梯形的面积计算公式。

师：请用你准备的七巧板，动手摆一个图案，并说说你的图案都用了哪些简单图形？(教师参与到学生的七巧板活动中，特别是要关心后进生的动手情况。

)师：同桌互相看一看、说一说，你们拼的这个图形是由哪些图形拼成的？学生活动。

师：大家都有了自己的设计成果，来展示一下吧！选取几个有创意的图案在实物投影仪上展示，让学生分别汇报。

师：请仔细观察这些图案，它们有什么共同的地方？让学生发表意见。

师：说得真好！像这样由两个或两个以上简单的图形组合而成的图形，我们把它称为组合图形，今天我们就一起来探究组合图形面积的计算方法。

(板书课题：组合图形的面积)二、探索活动，寻求新知师：生活中有许多组合图形，老师准备了3幅图形，大家观察一下，这些组合图形是由哪些简单图形组成的？如果要求它们的面积可以怎样求？课件逐一出示图一、图二、图三，让学生发表意见。

预设：⎩⎪⎨⎪⎧图一：是由三角形、正方形再加上正方形中间的小正方形组成的，面积＝三角形面积＋正方形面积－小正方形面积。

多边形组合图形面积：五年级数学上册1．下图，一个梯形的上底是3cm，下底是5.5cm，高是2.8cm，在梯形中剪去一个最大的平行四边形，剩下的是个什么图形？它的面积是多少？解：剩下的是三角形，面积是：（5.5-3）×2.8÷2=2.5×2.8÷2=7÷2=3.5（平方厘米）答：剩下的是三角形，面积是3.5平方厘米。

2．下图是一块梯形菜地，涂色部分种茄子，空白部分种南瓜，种南瓜的面积是105m2，种茄子的面积是多少平方米？解：105×2÷15=210÷15=14（米）（15＋35）×14÷2-105=50×14÷2-105=700÷2-105=350-105=245（平方米）答：种茄子的面积是245平方米。

3．小冬家用50m长的竹篱笆，靠墙边围成了一块瓜地（见下图）。

如果平均每平方米地可以栽种4棵瓜苗，这块地可以栽种多少棵瓜苗？解：（50-20）×20÷2×4=600÷2×4=300×4=1200（棵）答：这块地可以栽种1200棵瓜苗。

4．计算组合图形的面积．（单位：厘米）解：8×6÷2+10×4=24+40=64（平方厘米）答：组合图形的面积是64平方厘米5．在一块梯形菜地(如右图)里种菜。

如果每棵菜占地0.6平方米，这块菜地可以种多少棵菜?解：（8+12）×5÷2÷0.6=20×5÷2÷0.6=50÷0.6答：这块地可以种83棵菜。

6．求如图所示组合图形的面积．（单位：厘米）解：图1，10×5=50（平方厘米）；答：这个平行四边形的面积是50平方厘米．×4×3=6（平方米）；图2，12答：这个三角形的面积是6平方米．×（8+4.5）×3图3，12×12.5×3=12=18.75（平方分米）；答：这个梯形的面积是18.75平方分米．图4，（10+4）×8−8×4×12=14×8﹣16=112﹣16=96（平方米）；答：这个组合图形的面积是96平方米7．计算下面图形的面积。