钢梁计算

简 支 钢 梁 计 算基本数据输入:梁跨度： l=9000mm梁间距a=2400mm钢材：Q 345f =315N/mm 2fv =185N/mm 2 上翼缘：b 1=400mm t 1=14mm 下翼缘：b 2=300mm t 2=12mm 腹 板：h w =574mm t w =8mm即: 断面截面特性计算：钢梁截面：A 0=13792mm 2 重量108.3kg/m 钢梁中和轴的位置：y 0=342mm钢梁对X轴截面惯性矩：I z =8.94E+08mm4钢梁上翼缘的弹性抵抗矩：W 1x = 3.46E+06mm 3 钢梁下翼缘的弹性抵抗矩：W 2x = 2.61E+06mm 3 钢梁对Y轴截面惯性矩：I y = 1.02E+08mm 4i y =85.9 mm y =104.8上翼缘对Y 轴的惯性矩：I 1=7.47E+07mm 4下翼缘对Y 轴的惯性矩：I 2= 2.70E+07mm 40.73 截面不对称影响系数：0.380.53 工字形截面简支梁的系数0.76 梁的整体稳定系数：0.74 修正后：0.672.截面验算：（1）弯矩及剪力的计算：=+=211I I I b α=-=)12(8.0b b αη=bβ==hb t l 111ξ=bφ='bφλ钢梁自重： 1.30KN/m恒载： 4.00KN/m2g1k=10.90KN/m活载：q c= 3.0KN/m2p k=18.10KN/m p=23.16KN/m 弯矩：M=234.49KN·m剪力：V=104.22KN（2）钢梁的强度、稳定和挠度的验算：梁的整体稳定应力：σ=101.01N/mm2钢梁上翼缘应力：σ1=67.70N/mm2钢梁下翼缘应力：σ2=89.68N/mm2钢梁剪应力：τ=22.70N/mm2挠度：w=8.4mmw/l=1/1072。

钢梁重量计算
钢梁重量计算是计算梁体重量的过程，梁体重量是指梁体内主要成分（钢材）的实际重量。

根据梁体的形状和材料性质，我们可以计算出梁体的重量。

具体计算步骤如下：
1、首先要确定钢材的类型和规格，例如，25mm的热轧薄板钢材；
2、然后确定钢材的折合厚度，折合厚度指的是实际使用的钢材厚度加上螺钉和其它结构连接件所占用的厚度。

3、根据折合厚度计算材料面积，单位面积的重量是多少，比如：单位面积的薄板钢材的重量为7855g/㎡；
4、最后将材料面积乘以单位面积的重量，就可以计算出梁体的重量。

盈建科钢梁计算结果摘要：一、引言二、盈建科钢梁计算结果的具体内容1.钢梁的截面性能计算2.钢梁的强度与刚度计算3.钢梁的稳定性计算三、盈建科钢梁计算结果的优缺点分析1.优点2.缺点四、结论正文：一、引言盈建科钢梁计算结果是建筑行业中的一项重要参考指标，对于建筑设计师、结构工程师以及其他相关人员而言，准确且可靠的计算结果是保障建筑安全性和可靠性的重要依据。

本文将对盈建科钢梁计算结果进行详细的阐述和分析，以便于相关人员对其有更深入的了解和应用。

二、盈建科钢梁计算结果的具体内容1.钢梁的截面性能计算盈建科钢梁计算结果中的截面性能计算主要包括以下几个方面：（1）截面惯性矩的计算（2）截面极惯性矩的计算（3）截面主惯性轴的计算2.钢梁的强度与刚度计算钢梁的强度与刚度计算是评估钢梁承载能力和变形能力的重要依据，盈建科钢梁计算结果主要包括以下几个方面：（1）强度计算（2）刚度计算3.钢梁的稳定性计算盈建科钢梁计算结果中的稳定性计算主要包括以下几个方面：（1）弯曲稳定性计算（2）扭转稳定性计算（3）剪切稳定性计算三、盈建科钢梁计算结果的优缺点分析1.优点盈建科钢梁计算结果具有较高的准确性，能够为建筑行业提供可靠的数据支持。

同时，其计算方法成熟，易于操作，方便相关人员应用。

2.缺点然而，盈建科钢梁计算结果也存在一定的局限性，例如，对于特殊类型的钢梁，其计算结果可能存在偏差。

此外，由于建筑行业的复杂性，盈建科钢梁计算结果并不能完全满足所有情况下的需求，需要结合实际情况进行调整和优化。

四、结论总的来说，盈建科钢梁计算结果是建筑行业中一项重要的参考指标，其准确性和可靠性得到了广泛认可。

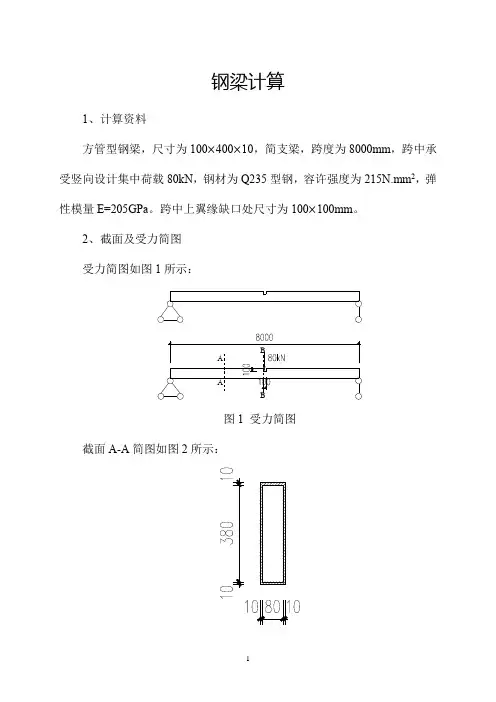
钢梁计算1、计算资料方管型钢梁，尺寸为100 400 10，简支梁，跨度为8000mm ，跨中承受竖向设计集中荷载80kN ，钢材为Q235型钢，容许强度为215N.mm 2，弹性模量E=205GPa 。

跨中上翼缘缺口处尺寸为100 100mm 。

2、截面及受力简图 受力简图如图1所示：图1 受力简图截面A-A 简图如图2所示：图2 A-A截面简图截面B-B简图如图3所示：图3 B-B右截面简图3、荷载计算跨中弯矩M1=跨中剪力V1=A-A截面Ix1=B-B右截面：形心：x=50mm，y=（）=132.94mm则Ix2=（）（）4、受弯强度验算没开缺口前跨中强度为：σ下=h下==191N.mm2(下部受拉)215 N.mm2σ上=h上==191N.mm2(上部收压)215N.mm2开个缺口后跨中强度为：σ下=h下=355.41 N.mm2(下部受拉)215N.mm2σ下=h下=（）448 N.mm2(上部收压)215N.mm2通过对比可以发现，当钢梁开一个小缺口之后，钢梁的抗弯强度会降低许多，本题计算下强度最大降低约为448/191=2.35倍之多。

5、受剪强度验算没开缺口前跨中截面惯量为：Sx=80010195+102002100=556000 mm3τ===6.64 N.mm2开缺口后跨中截面惯量为：Sx=102=279090.44 mm3τ===9.33 N.mm2通过对比可以发现，当钢梁开一个小缺口之后，钢梁的抗剪强度也会降低。

6、变形计算图4 变形计算简图简支梁我们考虑其最大变形，其发生位置在跨中，为此，我们计算跨中的最大变形。

当钢梁没有开缺口时M(x)=（）根据材料力学积分法求弯曲变形公式可得EI W(x)` =EI W(x)=根据积分得W(x)=最大变形在x=L/2处，得最大变形为w===24.848mm当钢梁开缺口时，计算方法同上：W(x)`==++CW(x)=++Cx+Dx=0时，W(x)=0，则D=0x=L/2时，W(x)`=0，则C=-(+)所以W(x)=+-(+)x其中I1=, I2=，所以跨中变形-W(x=L/2)=+-(+)L/2=+-(+)8000/2 =-89.402mm即W(x=L/2)= 89.402mm通过对比发现，当开一个缺口之后，梁的变形增加很大，增加约89.402/24.848=3.6倍之多。

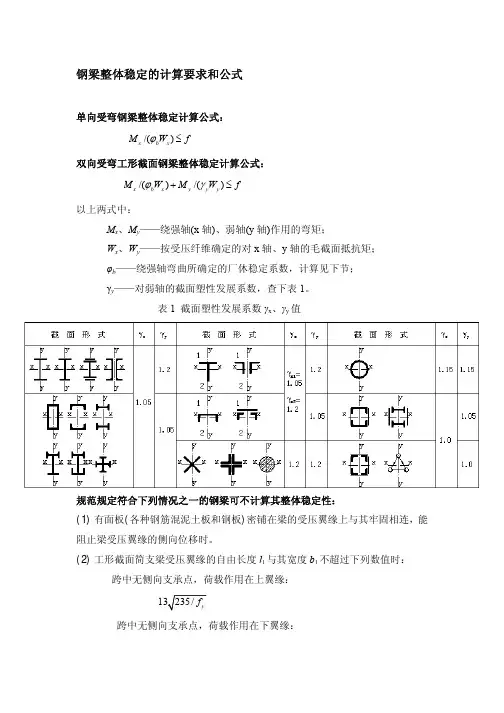
钢梁整体稳定的计算要求和公式
单向受弯钢梁整体稳定计算公式：
/()x b x M W f ϕ≤
双向受弯工形截面钢梁整体稳定计算公式：
/()/()x b x y y y M W M W f ϕγ+≤
以上两式中：
M x 、M y ——绕强轴(x 轴)、弱轴(y 轴)作用的弯矩；
W x 、W y ——按受压纤维确定的对x 轴、y 轴的毛截面抵抗矩； φb ——绕强轴弯曲所确定的厂休稳定系数，计算见下节；
γy ——对弱轴的截面塑性发展系数，查下表1。

表1 截面塑性发展系数γx 、γy 值
规范规定符合下列情况之一的钢梁可不计算其整体稳定性：
(1) 有面板(各种钢筋混泥土板和钢板)密铺在梁的受压翼缘上与其牢固相连，能阻止梁受压翼缘的侧向位移时。

(2) 工形截面简支梁受压翼缘的自由长度l 1与其宽度b 1不超过下列数值时： 跨中无侧向支承点，荷载作用在上翼缘：
跨中无侧向支承点，荷载作用在下翼缘：
跨中有侧向支承点：
(3)箱形截面(图1)简支梁的截面高宽比h/b≤6且l1/b0≤95(235/f y)时。

当采用箱形截面时，这一点很容易满足。

钢梁线刚度计算公式
钢梁线刚度是指在受外力作用下，钢梁所产生的形变与受力的关系。

钢梁的刚度一般用弹性模量(E)来表示，而钢梁的弹性模量与截面形状、材料及长度有关。

计算钢梁线刚度需要使用以下公式：
EI = kFL^2
其中，EI为钢梁的弯曲刚度， k为钢梁的截面形状系数，F为施加在钢梁上的力，L为钢梁的长度。

钢梁线刚度计算公式是钢结构设计中非常重要的公式之一，通过使用这个公式，可以预测钢梁在受力下的行为，有助于设计师更好地设计出满足要求的钢结构。

- 1 -。

第五章钢梁计算原理5.1 概述在钢结构中，承受横向荷载作用的实腹式构件称为梁类构件，即钢梁。

钢梁在土木工程中应用很广泛，例如厂房建筑中的工作平台梁、吊车梁、屋面檩条和墙架横梁，以及桥梁、水工闸门、起重机、海上采油平台中的梁等。

按制作方法可将钢梁分为型钢梁和组合梁两种。

型钢梁制作简单，成本较低，应用较广。

型钢梁通常采用热轧工字钢、槽钢、H型钢和T型钢（图5－1（a））以及冷弯薄壁型钢（图5－l（c））。

其中H型钢的截面分布最合理，其翼缘内外边缘平行，方便与其他构件连接；槽钢的截面扭转中心在腹板外侧，一般受力情况下容易发生扭转，在使用时应尽量避免。

当荷载较大或跨度较大时，必须采用组合梁（图5－1（b））来提高截面的刚度和承载力，其中箱形截面梁的抗扭强度较高。

组合梁的截面可以根据具体受力情况合理布置，达到节省钢材的目的。

图5－1表示出了两个正交的形心主轴，其中绕x轴的惯性矩、截面抵抗矩最大，称为强轴，另一轴则为弱轴。

对于工形、T形、箱形截面，平行于x轴(弯曲轴)的最外边板称为翼缘，垂直于x轴的板称为腹板。

按支承条件又可将梁分为简支梁、连续梁和悬伸梁等。

其中简支梁应用最广，因其制造、安装、拆换都较方便，而且受温度变化和支座沉陷的影响很小。

梁的设计必须同时满足承载能力极限状态和正常使用极限状态。

钢梁的承载能力极限状态包括强度、整体稳定和局部稳定三个方面。

设计时要求在荷载设计值作用下，梁的抗弯强度、抗剪强度、局部承压强度和折算应力均不超过相应的强度设计值；保证梁不会发生整体失稳；同时保证组成梁的板件不出现局部失稳。

正常使用极限状态主要指梁的刚度，设计时要求在荷载标准值作用下梁具有符合规范要求的足够的抗弯刚度。

图5－1钢梁常用截面类型5.2钢梁的强度和刚度5.2.1 梁的强度梁的强度包括抗弯强度、抗剪强度、局部承压强度和折算应力，设计时要求在荷载设计值作用下，均不超过《钢结构设计规范》规定的相应的强度设计值。

钢梁计算长度范文钢梁是一种常见的结构材料，在工程中常用于承受重力荷载和侧向荷载的建筑组件。

在进行钢梁计算时，需要考虑多个因素，包括材料的强度、截面形状、支承条件等。

下面将介绍钢梁计算中的一些关键步骤和注意事项。

首先，要计算钢梁的长度，需要确定其受力情况和支承条件。

钢梁通常是沿水平方向布置的，其长度可以根据实际需要进行确定。

受力情况包括重力荷载和侧向荷载，需要根据设计要求和实际工程情况进行合理的估计。

在进行钢梁计算时，还需确定其截面形状和尺寸。

常见的钢梁截面形状包括I型、H型、C型等，每种形状都有不同的特性和适用范围。

截面尺寸可以根据受力情况进行选择，通常通过进行弹性稳定性和强度计算来确定合适的尺寸。

弹性稳定性计算是针对钢梁在受力过程中是否会发生屈曲失稳现象的计算。

屈曲失稳是指当钢梁受到较大的压力或弯矩作用时出现的材料屈曲现象，此时钢梁的截面可能会变形或破坏。

因此，在计算钢梁长度时，需要通过考虑截面形状、尺寸和材料的强度等因素，来判断钢梁是否具有足够的弹性稳定性。

强度计算是对钢梁在受力过程中能否承受荷载而不发生破坏的计算。

钢梁的强度取决于截面形状、尺寸和材料的强度等因素。

对于不同类型的钢材，其强度值有所不同，需要根据实际情况进行选择。

在确定强度时，通常使用极限强度设计方法，即强度设计值要大于设计荷载，以确保结构的安全性。

除了弹性稳定性和强度计算，还需要考虑其他因素如挠度和疲劳寿命等。

钢梁在受力过程中会产生一定的挠度，对于较大跨度的钢梁，需通过计算来确定其挠度是否满足要求。

此外，疲劳寿命是指钢梁在反复荷载作用下是否会发生疲劳失效，对于需要经常受到荷载变化的钢梁结构，需进行疲劳寿命计算，以确保其使用寿命。

总结来说，钢梁计算长度需要考虑受力情况、截面形状、尺寸、弹性稳定性、强度、挠度和疲劳等因素。

根据这些因素进行综合计算，可以得到合理的钢梁长度，以确保结构的安全性和可靠性。

钢梁工程量计算公式
钢梁工程量计算公式是指在建筑工程中，计算钢梁所需材料和工程量的公式。

以下是钢梁工程量计算公式的详细创作：
1. 钢梁长度计算公式
钢梁长度计算公式为：L = (L1 + L2 + L3 + … + Ln) + 2Lc
其中，L为钢梁的总长度，L1、L2、L3、…、Ln为钢梁的各段长度，Lc为钢梁两端的连接长度。

2. 钢梁截面积计算公式
钢梁截面积计算公式为：A = b × h
其中，A为钢梁的截面积，b为钢梁的宽度，h为钢梁的高度。

3. 钢梁重量计算公式
钢梁重量计算公式为：W = A × L × ρ
其中，W为钢梁的重量，A为钢梁的截面积，L为钢梁的长度，ρ为钢梁的密度。

4. 钢梁材料计算公式
钢梁材料计算公式为：M = W ÷ ρ
其中，M为钢梁所需的材料量，W为钢梁的重量，ρ为钢梁的密度。

以上是钢梁工程量计算公式的详细创作，可以根据具体的建筑工程需要进行使用。

钢梁承重计算公式
钢梁承重计算公式是建筑工程中非常重要的一部分，它可以帮助工程师计算出钢梁的承重能力，从而保证建筑物的安全性。

在本文中，我们将详细介绍钢梁承重计算公式的相关知识。

我们需要了解一些基本概念。

钢梁是一种常用的建筑材料，它通常用于支撑建筑物的重量。

钢梁的承重能力取决于其截面积、材料强度和长度等因素。

因此，在计算钢梁的承重能力时，我们需要考虑这些因素。

我们需要了解钢梁承重计算公式的具体内容。

一般来说，钢梁的承重能力可以用以下公式来计算：
F = σ × A
其中，F表示钢梁的承重能力，σ表示钢材的屈服强度，A表示钢梁的截面积。

这个公式的意思是，钢梁的承重能力等于钢材的屈服强度乘以钢梁的截面积。

需要注意的是，这个公式只适用于静态荷载情况下的计算。

如果钢梁承受的是动态荷载，那么我们需要使用其他的计算公式来计算其承重能力。

我们需要了解一些实际应用中的注意事项。

在实际应用中，我们需要根据具体情况来选择合适的钢梁规格和材料。

同时，我们还需要
考虑钢梁的支撑方式、连接方式等因素，以确保钢梁的承重能力得到充分发挥。

钢梁承重计算公式是建筑工程中非常重要的一部分。

通过了解钢梁的基本概念、计算公式和实际应用中的注意事项，我们可以更好地保证建筑物的安全性。

钢梁整体稳定性验算步骤（一）1.根据《钢结构设计规范》（GB50017-2003）4.2.1条，判断是否可不计算梁的整体稳定性。

2. 如需要计算2.1 等截面焊接工字形和轧制H 型钢简支梁b 1b 1t 1t 1hxx y yb 1b 2t 2xx y yht 1y(a)双轴对称焊接工字形截面(b)加强受压翼缘的单轴对称焊接工字形截面b 1b 2t 1xy y(c)加强受拉翼缘的单轴对称焊接工字形截面t 2x hb 1b 1t 1hxx y y(d)轧制H 型钢截面t 11）根据表B.1注1，求ξ。

l1——H 型钢或等截面工字形简支梁受压翼缘的自由长度，对跨中无侧向支承点的梁，l1为其跨度；对跨中有侧向支撑点的梁，l1为受压翼缘侧向支承点间的距离（梁的支座处视为有侧身支承）。

b1——截面宽度。

2）根据表B.1，求βb。

3）根据公式B.1-1注，求I1和I2，求αb。

如果αb>0.8，根据表B.1注6，调整βb。

4）根据公式B.1-1注，计算ηb。

5）根据公式B.1-1，计算φb。

6）如果φb>0.6，根据公式B.1-2，采用φ’b代替φb。

7）根据公式4.2.2，验算稳定性。

2.2 轧制普通工字钢简支梁1）根据表B.2选取φb。

2）如果φb>0.6，根据公式B.1-2，采用φ’b代替φb。

3）根据公式4.2.2，验算稳定性。

2.3 轧制槽钢简支梁1）根据公式B.3，计算φb。

2）如果φb>0.6，根据公式B.1-2，采用φ’b代替φb。

3）根据公式4.2.2，验算稳定性。

2.4 双轴对称工字形等截面（含H型钢）悬臂梁1）根据表B.1注1，求ξ。

l1——悬臂梁的悬伸长度。

b1——截面宽度。

2）根据表B.4，求βb。

3）根据公式B.1-1，计算φb。

4）如果φb>0.6，根据公式B.1-2，采用φ’b代替φb。

5）根据公式4.2.2，验算稳定性。

2.5 受弯构件整体稳定系数的近似计算（均匀弯曲，）2.5.1 工字形截面（含H型钢）双轴对称1）根据公式B.5-1，计算φb，当φb>0.6时，不必根据公式B.1-2，采用φ’b代替φb，当φb>1.0，取φb=1.0。