Lesson-02 节点导纳矩阵及节点网络方程的解法
- 格式：pdf
- 大小：5.03 MB
- 文档页数：64
下载文档原格式
合集下载
节点导纳矩阵法
n
n
节点电压u j 可为任何值 → 各项系数为零
∑y
k =1
n
k1
= ∑ yk 2 = L = ∑ ykn = 0
k =1 k =1
10
n
n
z 性质二：行元素之和为零。
假设各节点电位都相等且不为零（u1 =u2 = L =un ≠ 0）。 由于节点间无电位差，所以各电流都为零。 ik = −∑ u j ykj = 0
18
微波半导体器件
根据基尔霍夫电流定律： I1 + jωC2 (V2 − V1 ) + ( G1 + jωC1 )(V3 − V1 ) = 0 I 2 + jωC2 (V1 − V2 ) + ( G2 + jωC3 )(V3 − V2 ) − g m (V1 − V3 ) = 0 I 3 + ( G1 + jωC1 )(V1 − V3 ) + ( G2 + jωC3 )(V2 − V3 ) + g m (V1 − V3 ) = 0
20
利用S参数求待定导纳矩阵 实际电路中尚有一些微波元器件，它们 的导纳矩阵或等效电路中 Ykj 不可能精确的 从理论分析中导出。对于这类元器件，一般 采用测量方法测出其散射矩阵参数，然后将 它变换成导纳矩阵参数，再求出待定导纳矩 阵。
21
利用S参数求待定导纳矩阵
[S ] → [ y] :
% ] = ([ I ] − [ S ]) ([ I ] + [ S ]) [y ⎤ % ⎡ ⎤ [ y] = ⎡ ⎣ y0 ⎦ [ y ] ⎣ y0 ⎦
7
节点电流方程（基尔霍夫电流定律）
写成向量形式： I = YU Y : 待定导纳矩阵 I : 外电流向量 U : 节点电压向量 其中 − ykk = ∑ ykj
节点导纳矩阵法
Y1(23)
Y1(13)
⎥ ⎦
所以：
[ ]y = ⎡⎢⎢YY13((1111))
⎢ ⎢⎣ 0
Y1(31) Y3(31) + Y1(12) + Y2(23)
Y2(12) + Y1(23)
21
利用S参数求待定导纳矩阵
[S] → [ y]:
[ y%] = ([I ] −[S])([I ] + [S])−1
[ y] = ⎡⎣ y0 ⎤⎦[ y%] ⎡⎣ y0 ⎤⎦
其中[ y%]为归一化导纳矩阵，[I ]为单位矩阵，
⎡⎣
⎡
y0
⎤⎦
=
⎢ ⎢
y01
O
0
⎤ ⎥
⎥
⎢ ⎢⎣
0
y0n
⎥ ⎥⎦
y01, y02 ,L, y0n为n端口元件各端外接传输线特性导纳。
3.2 节点导纳矩阵法（待定导纳矩阵法） Admittance Matrix Method
1
一般电路
端点：元件与外部连线的衔接点； 端口：电路网络的输入与输出口， 一个端口由两个端点构成； 节点：元件与元件的端点互相连接 之处； 支路：两个节点之间的通路； 回路：由一个节点出发，再回到该 节点的一组支路。
k =1
k =1
k =1
10
z 性质二：行Βιβλιοθήκη 素之和为零。假设各节点电位都相等且不为零（u1=u2 =L=un ≠ 0）。 由于节点间无电位差，所以各电流都为零。
n
∑ ik = − u j ykj = 0 j =1
k = 1, 2,L, n
又由于u1=u2 =L=un ≠ 0，所以
n
n
n
∑ ∑ ∑ y1 j = y2 j = L = ynj = 0
节点导纳矩阵的计算及应用综述
图 1 经典电力网络节点图
接下来将以上述图示 2 为例进行推导，上述 点网络表述成式(1)
图示节点网络有 5 个节点、6 条支路、y1-y6
为各条支路的导纳。
由 KCL(基尔霍夫电流定律)可以将上述节
V V V V V
y
4
2
1
y
5
3
1
y6
有许多比较明显的特点，一一列举如下： （1）节点导纳矩阵是对称矩阵，关于
主对角线对称； （2）节点导纳矩阵是稀疏矩阵，矩阵
内含有大量的零元素； （3）自导纳位于矩阵对角线，为与节
点相连接的导纳之和； （4）互导纳位于矩阵非对角线位置，
为两节点之间导纳的相反数； （5）导纳矩阵维数与节点数相等； 相对于节点阻抗矩阵，节点导纳矩阵具
为了便于后续章节的展开，首先对一些 名词进行必要的解释。 （1）节点：
若干元件的汇合点，节点的特征是每一 个瞬时电压相等。 （2）节点的选择：
节点和系统短路发生点基本一致，因有 可能发生短路而需要被列为短路点进行计 算的点均被看作一个节点，比如各条母线、 发电机出口、变压器高低压侧等。 （3）节点的分类：
单独作用时产生的响应之和。 将式(2)与式(3)作对比可得式(4)和式(5)
Y 11 y 4 y 5 y 6
Y
22
Y 33
y1 y 3 y 4 y2 y3 y5
Y
44
y1
(4)
Y 55 y 2
自导纳
Y Y Y
12 13 23
Y
21
节点导纳矩阵及潮流计算
目录摘要 (2)1任务及题目要求 (2)2原理介绍 (3)2.1节点导纳矩阵 (3)2.2牛顿-拉夫逊法 (4)2.2.1牛顿-拉夫逊法基本原理 (4)2.2.2牛顿--拉夫逊法潮流求解过程介绍 (6)3分析计算 (11)4结果分析 (15)5总结 (16)参考资料 (17)节点导纳矩阵及潮流计算摘要电力网的运行状态可用节点方程或回路方程来描述。
节点导纳矩阵是以系统元件的等值导纳为基础所建立的、描述电力网络各节点电压和注入电流之间关系的线性方程。
潮流计算是电力系统分析中的一种最基本的计算，它的任务是对给定的运行条件确定系统的运行状态，如各母线上的电压（幅值及相角）、网络中的功率分布及功率损耗等。
本文就节点导纳矩阵和潮流进行分析和计算。
1任务及题目要求题目初始条件：如图所示电网。
1∠002阵Y；2+j13）给出潮流方程或功率方程的表达式；4）当用牛顿-拉夫逊法计算潮流时，给出修正方程和迭代收敛条件。
2原理介绍2.1节点导纳矩阵节点导纳矩阵既可根据自导纳和互导纳的定义直接求取，也可根据电路知识中找出改网络的关联矩阵，在节点电压方程的矩阵形式进行求解。
本章节我们主要讨论的是直接求解导纳矩阵。
根据节点电压方程章节我们知道，在利用电子数字计算机计算电力系统运行情况时，多采用IYV 形式的节点方程式。
其中阶数等于电力网络的节点数。
从而可以得到n 个节点时的节点导纳矩阵方程组：nn Y n +V （2-1） 由此可以得到n 个节点导纳矩阵：nn Y ⎫⎪⎪⎪⎪⎭它反映了网络的参数及接线情况，因此导纳矩阵可以看成是对电力网络电气特性的一种数学抽象。
由导纳短阵所了解的节点方程式是电力网络广泛应用的一种数学模型。
通过上面的讨论，可以看出节点导纳矩阵的有以下特点：（1）导纳矩阵的元素很容易根据网络接线图和支路参数直观地求得，形成节点导纳矩阵的程序比较简单。
（3）导纳矩阵是稀疏矩阵。
它的对角线元素一般不为零，但在非对角线元素中则存在不少零元素。
节点导纳矩阵及潮流计算
目录摘要 (2)1任务及题目要求 (2)2原理介绍 (3)节点导纳矩阵 (3)牛顿-拉夫逊法 (4)牛顿-拉夫逊法基本原理 (4)牛顿--拉夫逊法潮流求解过程介绍 (6)3分析计算 (11)4结果分析 (15)5总结 (16)参考资料 (17)节点导纳矩阵及潮流计算摘要电力网的运行状态可用节点方程或回路方程来描述。
节点导纳矩阵是以系统元件的等值导纳为基础所建立的、描述电力网络各节点电压和注入电流之间关系的线性方程。
潮流计算是电力系统分析中的一种最基本的计算，它的任务是对给定的运行条件确定系统的运行状态，如各母线上的电压（幅值及相角）、网络中的功率分布及功率损耗等。
本文就节点导纳矩阵和潮流进行分析和计算。
1任务及题目要求题目初始条件： 如图所示电网。
其元件导纳参数为：y 12=, y 23=, y 13=任务及要求:1）根据给定的运行条件，确定图2所示电力系统潮流计算时各节点的类型和待求量；2）求节点导纳矩阵Y ；1???2+j13）给出潮流方程或功率方程的表达式；4）当用牛顿-拉夫逊法计算潮流时，给出修正方程和迭代收敛条件。
2原理介绍节点导纳矩阵节点导纳矩阵既可根据自导纳和互导纳的定义直接求取，也可根据电路知识中找出改网络的关联矩阵，在节点电压方程的矩阵形式进行求解。
本章节我们主要讨论的是直接求解导纳矩阵。
根据节点电压方程章节我们知道，在利用电子数字计算机计算电力系统运行情况时，多采用IYV 形式的节点方程式。
其中阶数等于电力网络的节点数。
从而可以得到n 个节点时的节点导纳矩阵方程组：11112211211222221122n n n n nn n Y Y Y n Y Y Y n Y Y Y n +++=⎫⎪+++=⎪⎬⎪⎪+++=⎭V V V I V V V I V V VI （2-1） 由此可以得到n 个节点导纳矩阵：111212212212n n n n nn Y Y Y Y Y Y Y Y Y Y ⎛⎫⎪ ⎪= ⎪⎪⎝⎭? （2-2） 它反映了网络的参数及接线情况，因此导纳矩阵可以看成是对电力网络电气特性的一种数学抽象。
电力网节点导纳矩阵计算例题与程序
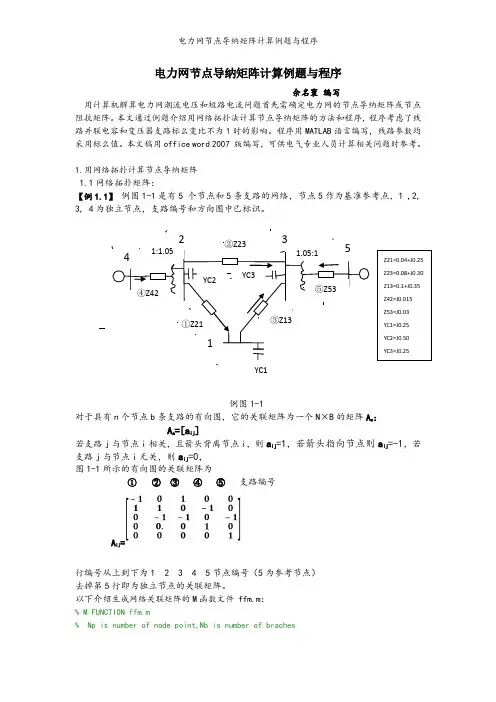
电力网节点导纳矩阵计算例题与程序佘名寰 编写用计算机解算电力网潮流电压和短路电流问题首先需确定电力网的节点导纳矩阵或节点阻抗矩阵。
本文通过例题介绍用网络拓扑法计算节点导纳矩阵的方法和程序，程序考虑了线路并联电容和变压器支路标么变比不为1时的影响。
程序用MATLAB 语言编写，线路参数均采用标么值。
本文稿用office word 2007 版编写，可供电气专业人员计算相关问题时参考。
1.用网络拓扑计算节点导纳矩阵 1.1网络拓扑矩阵：【例1.1】 例图1-1是有5 个节点和5条支路的网络，节点5作为基准参考点，1 ,2, 3, 4为独立节点，支路编号和方向图中已标识。
例图1-1对于具有n 个节点b 条支路的有向图，它的关联矩阵为一个N ×B 的矩阵A a ：A a =[a ij ]若支路j 与节点i 相关，且箭头背离节点i ，则a ij =1，若箭头指向节点则a ij =-1，若支路j 与节点i 无关，则a ij =0，图1-1所示的有向图的关联矩阵为① ② ③ ④ ⑤ 支路编号A ij =行编号从上到下为1 2 3 4 5节点编号（5为参考节点） 去掉第5行即为独立节点的关联矩阵。
以下介绍生成网络关联矩阵的M 函数文件 ffm.m ：% M FUNCTION ffm.m% Np is number of node point,Nb is number of braches ②Z23③Z13①Z21YC2YC3YC1④Z42⑤Z531:1.051.05:142315Z21=0.04+J0.25 Z23=0.08+J0.30 Z13=0.1+J0.35 Z42=J0.015 Z53=J0.03 YC1=J0.25 YC2=J0.50 YC3=J0.25% nstart--the start point of branches ,nend -- the end point,% A -- network incidence matrixfunction[A]=ffm(nstart,nend)global Np Nbn=length(nstart);A=zeros(Np,Nb);for i=1:nA(nstart(i),i)=1;A(nend(i),i)=-1;end以例图1-1网络为例调用ffm.m文件求其关联矩阵运算以上程序可得关联矩阵 mm ij如下：mm =-1 0 1 0 01 1 0 -1 00 -1 -1 0 -10 0 0 1 00 0 0 0 1Mm ij明显与A ij是相同的。
电力网节点导纳矩阵计算例题与程序
电⼒⽹节点导纳矩阵计算例题与程序电⼒⽹节点导纳矩阵计算例题与程序佘名寰编写⽤计算机解算电⼒⽹潮流电压和短路电流问题⾸先需确定电⼒⽹的节点导纳矩阵或节点阻抗矩阵。
本⽂通过例题介绍⽤⽹络拓扑法计算节点导纳矩阵的⽅法和程序，程序考虑了线路并联电容和变压器⽀路标么变⽐不为1时的影响。
程序⽤MATLAB 语⾔编写，线路参数均采⽤标么值。
本⽂稿⽤office word 2007 版编写，可供电⽓专业⼈员计算相关问题时参考。
1.⽤⽹络拓扑计算节点导纳矩阵 1.1⽹络拓扑矩阵：【例1.1】例图1-1是有5 个节点和5条⽀路的⽹络，节点5作为基准参考点，1 ,2, 3, 4为独⽴节点，⽀路编号和⽅向图中已标识。
例图1-1对于具有n 个节点b 条⽀路的有向图，它的关联矩阵为⼀个N ×B 的矩阵A a ：A a =[a ij ]若⽀路j 与节点i 相关，且箭头背离节点i ，则a ij =1，若箭头指向节点则a ij =-1，若⽀路j 与节点i ⽆关，则a ij =0，图1-1所⽰的有向图的关联矩阵为①②③④⑤⽀路编号 A ij =[ ?10100110?100?1?10?100.01000001]⾏编号从上到下为1 2 3 4 5节点编号（5为参考节点）去掉第5⾏即为独⽴节点的关联矩阵。
以下介绍⽣成⽹络关联矩阵的M 函数⽂件 ffm.m ：% M FUNCTION ffm.m% Np is number of node point,Nb is number of braches% nstart--the start point of branches ,nend -- the end point, % A -- network incidence matrix function [A]=ffm(nstart,nend) global Np Nb n=length(nstart); A=zeros(Np,Nb); for i=1:nA(nstart(i),i)=1; A(nend(i),i)=-1; end以例图1-1⽹络为例调⽤ffm.m ⽂件求其关联矩阵运算以上程序可得关联矩阵 mm ij 如下：mm =-1 0 1 0 0 1 1 0 -1 0 0 -1 -1 0 -1 0 0 0 1 0 0 0 0 0 1 Mm ij 明显与A ij 是相同的。
电力网络数学模型
（4-3）
或
Y11 Y12 Y Y 21 22 Yn1 Yn 2
Y1n V1 I1 Y2 n V2 I 2 Ynn Vn In
记成
YV =I
7
电气信息工程系
Yik yik
(3)不难理解Yki=Yik 。若节点i和k没有支路直接相联时，便有Yki=Yik=0
10
电气信息工程系
节点导纳矩阵的主要特点是：
①
② ③
导纳矩阵的元素很容易根据网络接线图和支路参数 直观地求得; nn阶对称复数方阵; 导纳矩阵是稀疏矩阵。它的对角线元素一般不为零， 但在非对角线元素中则存在不少零元素。如果在程 序设计中设法排除零元素的贮存和运算，就可以大 大地节省贮存单元和提高计算速度。
j 0.016 j 0.02
1 1 1 0.024 j 0.065 0.03 j 0.08 1.052 j 0.105
9.1085 j 33.1002 1 1 Y23 Y32 4.9989 j13.5388 z23 0.024 j 0.065 z12 2 1 1 1 Y24 Y42 z24 0.03 j 0.08
11
电气信息工程系
讨论网络中含有非基准变比的变压器时导纳矩阵元素的计算。
设节点p、q间接有变压支路，如图4-3所示。根据Π型等值电路， 可以写出节点p、q的自导纳和节点间的互导纳分别为：
1 k 1 1 YPP kz kz z 1 1 k 1 Yqq 2 2 kz k z k z 1 Ypq Yqp kz
5
I 4 y40 E4 ，分别称为节点1和4 其中 I1 y10 E1 和 的注入电流源。 以零电位点作为计算节点电压的参考点，根据基尔霍夫 电流定律，写出4个独立节点的电流平衡方程如下：
或
Y11 Y12 Y Y 21 22 Yn1 Yn 2
Y1n V1 I1 Y2 n V2 I 2 Ynn Vn In
记成
YV =I
7
电气信息工程系
Yik yik
(3)不难理解Yki=Yik 。若节点i和k没有支路直接相联时，便有Yki=Yik=0
10
电气信息工程系
节点导纳矩阵的主要特点是：
①
② ③
导纳矩阵的元素很容易根据网络接线图和支路参数 直观地求得; nn阶对称复数方阵; 导纳矩阵是稀疏矩阵。它的对角线元素一般不为零， 但在非对角线元素中则存在不少零元素。如果在程 序设计中设法排除零元素的贮存和运算，就可以大 大地节省贮存单元和提高计算速度。
j 0.016 j 0.02
1 1 1 0.024 j 0.065 0.03 j 0.08 1.052 j 0.105
9.1085 j 33.1002 1 1 Y23 Y32 4.9989 j13.5388 z23 0.024 j 0.065 z12 2 1 1 1 Y24 Y42 z24 0.03 j 0.08
11
电气信息工程系
讨论网络中含有非基准变比的变压器时导纳矩阵元素的计算。
设节点p、q间接有变压支路，如图4-3所示。根据Π型等值电路， 可以写出节点p、q的自导纳和节点间的互导纳分别为：
1 k 1 1 YPP kz kz z 1 1 k 1 Yqq 2 2 kz k z k z 1 Ypq Yqp kz
5
I 4 y40 E4 ，分别称为节点1和4 其中 I1 y10 E1 和 的注入电流源。 以零电位点作为计算节点电压的参考点，根据基尔霍夫 电流定律，写出4个独立节点的电流平衡方程如下：
节点导纳矩阵计算
（1-15）
（3）在网络的原有节点 i，j 之间切除一条导纳为 yij 的支路。这种情况可以 当作是在节点 i，j 间增加一条导纳为 yij 的支路来处理。因此，导纳矩阵中有关 元素的修正增量为：
Yii Y jj yij , Yij Y ji yij
（1-16）
（4）原网络节点 i，j 之间的导纳由 yij 改为 yij ' 。这种情况可以当作首先在节 点 i，j 间切除一条导纳为 yij 的支路，然后再在节点 i，j 间追加导纳为 yij ' 的支路， 根据式（1-15） 、 （1-16）不难求出导纳矩阵相关元素的修正量。 其他的网络变更情况， 可以仿照上述方法进修正公式。应该指出，如果增加或切除的支路是变 压器支路，则以上相关元素的修改应按式（1-12） 、 （1-13） 、 （1-14）进行。
P
Z
1:k
q
kz
P
kz k 1
q
k2z 1 k
Ypp
节点 q 的自导纳改变量：
1 k 1 1 kz kz z 1 1 k 1 2 2 kz k z k z 1 kz
Yqq
增加节点 p，q 间的互导纳：
（1-13）
Ypq Yqp
（1-14）
在电力系统中，假定接线改变前的导纳矩阵元素为 Yij(0) ，接线改变后则应修 改为 Yij Yij(0) Yij 。 现就几种典型的接线方式变化， 说明修改量 Yij 的计算方法。 （1）从网络的原有节点 i 引出一条导纳为 yij 的支路，同时增加一个节点 j。 由于节点数加 1，导纳矩阵将增加一行一列。新增的对角线元素 Y jj yij 。新增的 非对角线元素中，只有 Yij Y ji yij ，其余的元素都为零。矩阵的原有部分，只
节点导纳矩阵法
⎤ ⎥ ⎥⎦
⎡⎢⎣VV&&23
⎤ ⎥ ⎦
28
图解建立电路导纳矩阵的步骤
对于第三个元件有：
⎡ ⎢ ⎢
I&1(3) I&2(3)
⎤ ⎥ ⎥
=
⎢⎢⎡YY12((1133))
⎢ ⎢⎣
I&3(3)
⎥ ⎥⎦
⎢⎢⎣Y3(13)
Y1(23) Y2(23) Y3(23)
Y1(33) Y2(33) Y3(33)
⎤ ⎥ ⎥ ⎥ ⎥⎦
k =1
k =1
k =1
10
z 性质二：行元素之和为零。
假设各节点电位都相等且不为零（u1=u2 =L=un ≠ 0）。 由于节点间无电位差，所以各电流都为零。
n
∑ ik = − u j ykj = 0 j =1
k = 1, 2,L, n
又由于u1=u2 =L=un ≠ 0，所以
n
n
n
∑ ∑ ∑ y1 j = y2 j = L = ynj = 0
∑ ⎧
⎪i1
=
−
n
u j y1 j
⎪
j =1
∑ ⎪
n
⎪⎨i2
=
−
u j y2 j
j =1
⎪⎪M
∑ ⎪
⎪in
=−
n
u j ynj
⎩
j =1
6
节点电流方程（基尔霍夫电流定律）
全电路节点方程组：
⎛ ⎜ ⎜ ⎜
i1 i2 M
⎞ ⎟ ⎟ ⎟
=
⎛ ⎜ ⎜ ⎜
− −
y11 y21 M
− y12 − y22
M
L L
2
3.2.1 待定导纳矩阵的定义
电力系统分析第4章
（4-3）
第四章电力网络的数学模型
4.1 节点导纳矩阵
上式也可以用矩阵写成
Y11 Y12 L Y1 n Y Y 22 L Y 2 n 21 M M M Y n 1 Y n 2 L Y nn V 1 V 2 M V n I1 = I2 M I n
j
(4-7)
式中， i 0 为节点 i 与零电位点之间的支路导纳； y
第四章电力网络的数学模型
4.1 பைடு நூலகம்点导纳矩阵
当 k ≠i 时，公式（4-6）说明，当网络中除节 点 k 以外所有节点都接地时，从节点 i 流入网络 的电流同施加于节点 k 的电压之比。即等于节点 k 与 i 之间的互导纳 Yik ，即
Z11 Z 21 M Z n1
Z12 L Z1n I1 V 1 Z 22 L Z 2 n I 2 = V 2 M M M M Z n 2 L Z nn I n V n
（4-20）
第四章电力网络的数学模型
4.3 节点阻抗矩阵
k =1 i 1 ( ( Yik k 1)Ykjk 1) ( Ykkk 1)
Y ( n1)
其中
(i = 1,2, L , n; j = i, i + 1, L n)
第四章电力网络的数学模型
4.3 节点阻抗矩阵
一、节点阻抗局阵元素的物理意义 在电力系统计算中，节点方程也常写成阻抗形式，即 ZI = V （4-19） 式中， Z = Y 1 称为网络的节点阻抗矩阵。 方程式（4-19）可展开写成
代入（4－3）各式
Y
ik
=
I
i k
V
V
j
= 0 , j≠ k
(4-6)
第四章电力网络的数学模型
节点导纳矩阵.ppt
2 1 3 1 3 2 4 2 5 2
y y y y y
4 5 3 1 2
这些是各节点的互导纳；其余节点互导纳为0； 上式反映了各节点电压与注入电流的关系，I 1 ~ I 5 为各节点 注入的电流，除 I I 外其他都为0
1
5
通过以上的例子，节点方程的阶数等于网络的节点数n，展开一般 形式为：
导纳矩阵的对称性和稀疏性对于计算机解算电力系统问题有很大的影 响，如果能充分利用该特点，会大大提高计算机的速度并节约内存。
1.2节点导纳矩阵的形成与修改 主要分为三个部分：导纳矩阵的形成、特殊元件的处理与导纳矩阵的修 改。 导纳矩阵的形成可以分为以下几点： (1) 导纳矩阵的阶数等于电力网络的节点数； (2) 导纳矩阵各行的非对角元素中非零元素的个数等于对应节点所连的不 接地支路数； (3) 导纳矩阵各对角元素，即各节点的自导纳等于相应节点所连支路的导 纳之和：
节点2的自导纳应为：
Y22
(4) 导纳矩阵的非对角元素 纳并取负号：
1 y12 z12
等于节点 和节点 间的支路导
1 Yij yij zij
按照上述原则无论电力系统如何复杂都可以根据输电线路的参数和接线拓 扑，直接求出导纳矩阵。 一下包括变压器、移相器时，导纳矩阵的的形成方法。 当节点 i 、 j 之间为变压器支路时对导纳矩阵的影响： (1) 增加非零非对角元素
1
3
V1=1
I1I13I3 Nhomakorabeaz12 z10
z13
I10
I 1 I 12 I 13 I I 2 I I 3 I
12
节点导纳矩阵的原理
节点导纳矩阵的原理
节点导纳矩阵是以网络中某一点为参考点，以节点的自导纳和两节点间的共导纳为基础建立的矩阵。
在电力网络中，节点导纳矩阵用于描述各节点电压和注入电流之间的关系。
具体来说，节点导纳矩阵的对角元素Yij（i=j）表示节点自导纳，等于与该节点相连接的各支路导纳之和。
非对角线元素Yij （i≠j）表示互导纳，即直接连接两个节点的各支路导纳之和的相反数。
对于微波网络，节点导纳矩阵也是用端口电压（自变量）表示端口电流（因变量）的参量矩阵。
二端口网络可以用矩阵表示其节点导纳，例如当T₂面短路时，端口1的输入导纳；当T₁面短路时，端口2的输入导纳等。
以上内容仅供参考，建议查阅关于节点导纳矩阵的专业书籍或咨询专业人士获取更准确的信息。
节点导纳矩阵
节点导纳矩阵
节点导纳矩阵是一种重要的数学模型，它用来描述一个网络由端点和连接组成，其中端点有单个变量，它们之间的关系由算法控制。
它可以用来模拟复杂的系统，如电路、社会网络和计算机网络等。
它由一组可以在任何一个给定的节点上改变的变量组成，这些变量通常是电流或电压。
节点导纳矩阵可以用来模拟电路的行为，因为它能够表达电路中不同组件之间的关系。
可以将这种关系用一个导纳矩阵表示，这个矩阵描述了电路中每一节点之间的变化。
例如，一个两端口电路可以用一个2*2的导纳矩阵表示，它表示了每一端口之间的电流之间的关系。
此外，节点导纳矩阵还可以用来模拟社会网络中的行为。
这样的社会网络包括人与人之间的关系，也可以用导纳矩阵来模拟。
这样的社会网络可以用一个N*N的导纳矩阵来表示，它描述了每一个参与者之间的关系。
这样的社会网络可以用来模拟社会系统，如政治、社会和经济系统。
另一方面，节点导纳矩阵还可以用来模拟计算机网络。
计算机网络是由一系列节点和连接组成的复杂系统，它可以用一个N*N的导纳矩阵表示，用来描述每一节点之间的关系。
这样的网络可以用来模拟计算机系统，如互联网和局域网系统。
在总结，节点导纳矩阵是一种非常有用的数学模型，它可以用来模拟复杂的系统，如电路、社会网络和计算机网络等，用来描述
不同组件之间的关系。
它可以用一个N*N的导纳矩阵来表示，这个矩阵描述了每一个节点之间的变化，从而更好地模拟复杂的系统。
节点导纳矩阵在工程领域有着重要的作用，在未来的研究中有望取得更多有用的结果。
节点导纳矩阵及潮流计算
目录摘要 (2)1任务及题目要求 (2)2原理介绍 (3)2.1节点导纳矩阵 (3)2.2牛顿-拉夫逊法 (4)2.2.1牛顿-拉夫逊法基本原理 (4)2.2.2牛顿--拉夫逊法潮流求解过程介绍 (6)3分析计算 (11)4结果分析 (15)5总结 (16)参考资料 (17)节点导纳矩阵及潮流计算摘要电力网的运行状态可用节点方程或回路方程来描述。
节点导纳矩阵是以系统元件的等值导纳为基础所建立的、描述电力网络各节点电压和注入电流之间关系的线性方程。
潮流计算是电力系统分析中的一种最基本的计算，它的任务是对给定的运行条件确定系统的运行状态，如各母线上的电压（幅值及相角）、网络中的功率分布及功率损耗等。
本文就节点导纳矩阵和潮流进行分析和计算。
1任务及题目要求题目初始条件：如图所示电网。
1∠002阵Y；2+j13）给出潮流方程或功率方程的表达式；4）当用牛顿-拉夫逊法计算潮流时，给出修正方程和迭代收敛条件。
2原理介绍2.1节点导纳矩阵节点导纳矩阵既可根据自导纳和互导纳的定义直接求取，也可根据电路知识中找出改网络的关联矩阵，在节点电压方程的矩阵形式进行求解。
本章节我们主要讨论的是直接求解导纳矩阵。
根据节点电压方程章节我们知道，在利用电子数字计算机计算电力系统运行情况时，多采用IYV 形式的节点方程式。
其中阶数等于电力网络的节点数。
从而可以得到n 个节点时的节点导纳矩阵方程组：nn Y n +V （2-1） 由此可以得到n 个节点导纳矩阵：nn Y ⎫⎪⎪⎪⎪⎭它反映了网络的参数及接线情况，因此导纳矩阵可以看成是对电力网络电气特性的一种数学抽象。
由导纳短阵所了解的节点方程式是电力网络广泛应用的一种数学模型。
通过上面的讨论，可以看出节点导纳矩阵的有以下特点：（1）导纳矩阵的元素很容易根据网络接线图和支路参数直观地求得，形成节点导纳矩阵的程序比较简单。
（3）导纳矩阵是稀疏矩阵。
它的对角线元素一般不为零，但在非对角线元素中则存在不少零元素。
Lesson-02节点导纳矩阵及节点网络方程的解法
• 如果在节点i施加一单位电压，其余节点全部接地， 即
Vi 1, Vj 0, j 1, 2, , n, j i
Y11V1 Y12V2
Y1nVn
I1
Y21V1 Y22V2
Y2nVn
I
2
...
Yn1V1 Yn2V2 YnnVn In
I1
Y1i
I2 Y2i
Ii Yii
i7
y24
1 y12 i5 2 i6 y23
3
y34 i8 4
I1
i1
i2
y10
y20
i3
i4
y30
y40
I4
导纳形式的节点方程
y10V1 y12 (V1 V2 ) I1
y12 (V2
V1 )
y20V2
y23 (V2
V3 )
y24 (V2
V4 )
0
y23 (V3 V2 ) y34 (V3 V4 ) y30V3 0
李长松 Spring 2016
电力系统计算机辅助分析
稳定性计算
第5/6章
发电机组和 负荷数学模型
第4章
潮流计算
第2章
电力网络 数学模型
第1章
短路计算
第3章
什么是“数学模型”
• A mathematical model is a description for property or behavior of a system (or a process or a phenomenon) using mathematical concepts and language.
Y21V1 Y22V2
Y2nVn
I
2
Vi 1, Vj 0, j 1, 2, , n, j i
Y11V1 Y12V2
Y1nVn
I1
Y21V1 Y22V2
Y2nVn
I
2
...
Yn1V1 Yn2V2 YnnVn In
I1
Y1i
I2 Y2i
Ii Yii
i7
y24
1 y12 i5 2 i6 y23
3
y34 i8 4
I1
i1
i2
y10
y20
i3
i4
y30
y40
I4
导纳形式的节点方程
y10V1 y12 (V1 V2 ) I1
y12 (V2
V1 )
y20V2
y23 (V2
V3 )
y24 (V2
V4 )
0
y23 (V3 V2 ) y34 (V3 V4 ) y30V3 0
李长松 Spring 2016
电力系统计算机辅助分析
稳定性计算
第5/6章
发电机组和 负荷数学模型
第4章
潮流计算
第2章
电力网络 数学模型
第1章
短路计算
第3章
什么是“数学模型”
• A mathematical model is a description for property or behavior of a system (or a process or a phenomenon) using mathematical concepts and language.
Y21V1 Y22V2
Y2nVn
I
2
节点导纳矩阵节点电压方程
Sb2
Z~a1ZS~1a1(ZZ~~1a21
ZZ~~1b22)
S
2
Z~(aV1~aZ~V1~2b )VZ~Nb2
或写成：
S a1
Z~Ⅰ
S1
Z~Ⅱ Z~SΒιβλιοθήκη 2(V~a
Z~V~b )VN
Sb2
Z~Ⅰ
S1
Z~Ⅱ Z~
S
2
(V~b
Z~V~a )VN
式中：ZZ~~ⅠⅡ
S B S D S BC
S B S B S B
S AB
PB2 QB2 VN2
Z1
S A SB S AB
由VA
121k
V和S
向末端算电压。
A
V AB
PA R1 QA X 1 VA
VB VA VAB
VBC
PBR21 QB X 2 VB
S LD
图（b）
1
B2 D
A
图（c）
S LDb
S总目L录D 章目录 返回 上一页 下一页
图（a）所示系统，参数已归算到B侧，
给定：SLD，VD。（利用前一节公式计算） 将电压和功率由已知点向未知点交替递推
计算。
例3-2 系统如图（a)所示。已知： SLD，VD
Z L RL jX L ZT GT jBT S0 (GT jBT )VD2
1
arctg
V2
V2
V2
总目录 章目录 返回 上一页 下一页
2)若已知V1, S1求dV
dV1
P1R Q1 X V1
节点导纳矩阵及潮流计算
目录摘要 (2)1任务及题目要求 (2)2原理介绍 (3)2. 1节点导纳矩阵 (3)2. 2牛顿-拉夫逊法 (4)2. 2. 1牛顿-拉夫逊法基本原理 (4)2. 2. 2牛顿一拉夫逊法潮流求解过程介绍 (6)3分析计算 (11)4结果分析 (15)5总结 (16)参考资料 (17)节点导纳矩阵及潮流计算摘要电力网的运行状态可用节点方程或回路方程来描述。
节点导纳矩阵是以系统元件的等值导纳为基础所建立的、描述电力网络各节点电压和注入电流之间关系的线性方程.潮流计算是电力系统分析中的一种最基本的计算，它的任务是对给定的运行条件确定系统的运行状态，如各母线上的电压（幅值及相角）、网络中的功率分布及功率损耗等。
本文就节点导纳矩阵和潮流进行分析和计算。
1任务及题目要求题L1初始条件：其元件导纳参数为：y12= 0 o 5—j 3 , y：3=0. 8—j 4 , y13= 0 • 75—j2. 5任务及要求：1）根据给定的运行条件，确定图2所示电力系统潮流计算时各节点的类型和待求量;2）求节点导纳矩阵Y；3) 给出潮流方程或功率方程的表达式；4) 当用牛顿-拉夫逊法计算潮流时，给出修正方程和迭代收敛条件。
2原理介绍2. 1节点导纳矩阵节点导纳矩阵既可根据自导纳和互导纳的定义直接求取，也可根据电路知 识中找出改网络的关联矩阵，在节点电压方程的矩阵形式进行求解。
本章节我们 主要讨论的是直接求解导纳矩阵。
根据节点电压方程章节我们知道，在利用电 子数字讣算机讣算电力系统运行情况时，多采用IYV 形式的节点方程式。
其中阶 数等于电力网络的节点数。
从而可以得到n 个节点时的节点导纳矩阵方程组：力"+力"+…+儿小二1「Y2M + D2V2 +…二 12 >… (2KiV 1 + K,2V2+-+L t V/i = L一 1 )山此可以得到n 个节点导纳矩阵：1V (2)12Y =乙2… • • •厶…(2-2 )它反映了网络的参数及接线情况，因此导纳矩阵可以看成是对电力网络电 气特性的一种数学抽象。
节点导纳矩阵及潮流计算
目录摘要 (2)1任务及题目要求 (2)2原理介绍 (3)2.1节点导纳矩阵 (3)2.2牛顿-拉夫逊法 (4)2.2.1牛顿-拉夫逊法基本原理 (4)2.2.2牛顿--拉夫逊法潮流求解过程介绍 (6)3分析计算 (11)4结果分析 (15)5总结 (16)参考资料 (17)节点导纳矩阵及潮流计算摘要电力网的运行状态可用节点方程或回路方程来描述。
节点导纳矩阵是以系统元件的等值导纳为基础所建立的、描述电力网络各节点电压和注入电流之间关系的线性方程。
潮流计算是电力系统分析中的一种最基本的计算，它的任务是对给定的运行条件确定系统的运行状态，如各母线上的电压（幅值及相角）、网络中的功率分布及功率损耗等。
本文就节点导纳矩阵和潮流进行分析和计算。
1任务及题目要求题目初始条件：如图所示电网。
1∠002阵Y；2+j13）给出潮流方程或功率方程的表达式；4）当用牛顿-拉夫逊法计算潮流时，给出修正方程和迭代收敛条件。
2原理介绍2.1节点导纳矩阵节点导纳矩阵既可根据自导纳和互导纳的定义直接求取，也可根据电路知识中找出改网络的关联矩阵，在节点电压方程的矩阵形式进行求解。
本章节我们主要讨论的是直接求解导纳矩阵。
根据节点电压方程章节我们知道，在利用电子数字计算机计算电力系统运行情况时，多采用IYV 形式的节点方程式。
其中阶数等于电力网络的节点数。
从而可以得到n 个节点时的节点导纳矩阵方程组：nn Y n +V （2-1） 由此可以得到n 个节点导纳矩阵：nn Y ⎫⎪⎪⎪⎪⎭它反映了网络的参数及接线情况，因此导纳矩阵可以看成是对电力网络电气特性的一种数学抽象。
由导纳短阵所了解的节点方程式是电力网络广泛应用的一种数学模型。
通过上面的讨论，可以看出节点导纳矩阵的有以下特点：（1）导纳矩阵的元素很容易根据网络接线图和支路参数直观地求得，形成节点导纳矩阵的程序比较简单。
（3）导纳矩阵是稀疏矩阵。
它的对角线元素一般不为零，但在非对角线元素中则存在不少零元素。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
节点导纳矩阵的形成：p7
① 导纳矩阵阶数等于电力网络的节点数；
Y11 Y 21 Y31 Y41 Y12 Y32 Y13 Y33 Y14 V1 I1 Y24 V2 I 2 Y34 V3 I3 Y44 V I 4 4
发电 1
区域-2
电网仿真系统：IEEE 14 bus system
电网仿真系统：IEEE 30 bus system
电网仿真系统：IEEE 39 bus system
电网仿真系统：IEEE 118 bus system
导纳形式的节点方程
1 2
LD
4
四节点网络
LD
3
I1、I 4：节点注入电流
节点导纳矩阵的形成：p7
③ 各对角元素（即自导纳）：等于相应节点所连支路的导 纳之和；
Y11 Y 21 0 0 Y12 Y22 Y32 Y42 0 Y23 y23 y34 y30 Y43 0 V1 I1 Y24 V2 I 2 Y34 V3 I3 Y44 V I 4 4
natural sciences engineering disciplines social sciences
mathematical model
• A model may help to explain a system and to study the effects of different components, and to make predictions about behavior.
Yii yi 0 yij
ji
I1 Y1i I 2 Y2i I i Yii I n Yni
节点导纳矩阵元素的物理意义
• 节点i与节点j之间的互导纳：导纳矩阵第i列非对 角元素Yji，在数值上等于节点i施加单位电压，其 他节点都接地时，节点j向电力网络注入的电流。
再整理
Y V I Y11V 1 12 2 1 Y21V1 Y22V2 Y23V3 Y24V4 0 Y32V2 Y33V3 Y34V4 0 Y V Y V I Y42V 2 43 3 44 4 4
i7
y24
待求量是什么？
I 1
1 y12 i5 2 i6 y23 i1 i2
y10
3 i3
y30
y34
i8 4 i4
y40
y20
I 4
导纳形式的节点方程
y12 (V2 V1 ) y20V2 y23 (V2 V3 ) y24 (V2 V4 ) 0 y23 (V3 V2 ) y34 (V3 V4 ) y30V3 0 y24 (V4 V2 ) y34 (V4 V3 ) y40V4 I 4 y10V1 y12 (V1 V2 ) I1
导纳形式的节点方程
( y10 y12 )V1 y12V2 I1 y12V1 ( y12 y20 y23 y24 )V2 y23V3 y24V4 0 y23V2 ( y23 y34 y30 )V3 y34V4 0 y24V2 y34V3 ( y24 y34 y40 )V4 I 4
Y13 Y33 Y14 V1 I1 Y24 V2 I 2 Y34 V3 I3 Y44 V I 4 4
四节点网络
Y11 Y 21 Y31 Y41
Y12 Y32
Y11V1 Y12V2
Y1nVn I1 Y21V1 Y22V2 Y2 nVn I 2 ... Yn1V1 Yn 2V2 YnnVn I n
节点导纳矩阵元素的物理意义
• 节点i的自导纳：导纳矩阵第i列对角元素Yii，在数 值上等于节点i施加单位电压，其他节点都接地时， 节点i向电力网络注入的电流。 • 即：自导纳Yii是节点i以外的所有 节点都接地时节点i对地的总导纳。
Y ji y ji
• 而且有：
Y ji Y ji
I1 Y1i I 2 Y2i I i Yii I n Yni
节点导纳矩阵的主要特点
• Yij =Yji ，节点导纳矩阵具有对称性
• 若节点i和j没有支路直接相联时，则Yij = 0 • 导纳矩阵具有高度稀疏性，即非对角线元素中有 很多零元素 • 矩阵元素物理意义清楚，有规律可循，因而形成 节点导纳矩阵的程序简单
1 Ypq Yqp kz
节点导纳矩阵的修改
• 网络接线改变时节点导纳矩阵的修改
Y11 Y12 Y Y 21 22 Yn1 Yn 2
Y1n V1 I1 Y2 n V2 I 2 Ynn Vn In
n节点网络
导纳形式的节点方程
Y1nVn I1 Y21V1 Y22V2 Y2 nVn I 2 ... Yn1V1 Yn 2V2 YnnVn I n Y11V1 Y12V2
整理
( y10 y12 )V1 y12V2 I1
y12V1 ( y12 y20 y23 y24 )V2 y23V3 y24V4 0 y23V2 ( y23 y34 y30 )V3 y34V4 0 y24V2 y34V3 ( y24 y34 y40 )V4 I 4
Y11 y10 y12 Y12 y12 Y21 y12 Y12
说明什么？
导纳形式的节点方程
矩阵形式
Yij Y ji
Y V I Y11V 1 12 2 1 Y21V1 Y22V2 Y23V3 Y24V4 0 Y32V2 Y33V3 Y34V4 0 Y V Y V I Y42V 2 43 3 44 4 4
j 1
n
I YV
Y：节点导纳矩阵
节点导纳矩阵元素的物理意义
• 如果在节点i施加一单位电压，其余节点全部接地， 即
Vi 1, V j 0, j 1, 2,
, n, j i
I1 Y1i I 2 Y2i I i Yii I n Yni
i7
y24
I 1
1 y12 i5 2 i6 y23 i1 i2
y10
3 i3
y30
y34
i8 4 i4
y40
y20
I 4
导纳形式的节点方程
y12 (V2 V1 ) y20V2 y23 (V2 V3 ) y24 (V2 V4 ) 0 y23 (V3 V2 ) y34 (V3 V4 ) y30V3 0 y24 (V4 V2 ) y34 (V4 V3 ) y40V4 I 4 y10V1 y12 (V1 V2 ) I1
电力网络的数学模型
发电机的数学模型 负荷的数学模型
第1、2章
第4章 第4章
1.1 节点导纳矩阵 1.2 节点阻抗矩阵 1.3 电力网络方程的求解方法
电网仿真系统：WSCC9 system
GEN2-230 GEN3-230
发电 2
STNC-230
发电 3
区域-1
STNA-230
STNB-230
GEN1-230
节点导纳矩阵的形成：p7
④ 非对角元素（即互导纳）：等于相应节点之间的导纳的 负值。
Y11 Y 21 0 0 Y12 Y22 y 23 Y42 0 Y23 y23 y34 y30 Y43 0 V1 I1 Y24 V2 I 2 y34 V3 I3 Y44 V I 4 4
节点导纳矩阵的修改
• 网络中含有非标准变比的变压器支路时，导纳矩 阵元素的修改
节点导纳矩阵的修改
• 网络中含有非标准变比的变压器支路时导纳矩阵 元素的修改
• 节点p的自导纳改变量
1 k 1 1 Ypp kz kz z
• 节点q的自导纳改变量 • 增加节点p、q间的互导纳
1 1 k 1 Yqq 2 2 kz k z k z
Y22 Y23 Y42 Y43节点导纳矩阵的形成：p7
② 各行非对角元素中非零元素个数等于对应节点连接的不 接地支路数；
Y11 Y 21 0 0 Y12 Y32 0 Y33 Y22 Y23 Y42 Y43 0 V1 I1 Y24 V2 I 2 Y34 V3 I3 Y44 V I 4 4
Y11 Y12 Y Y 21 22 Yn1 Yn 2 Y1n V1 I1 Y2 n V2 I 2 Ynn Vn In
Y V I i ij j
Y22 Y23 Y42 Y43
YV = I
导纳形式的节点方程
节点电压 待求
YV = I
节点导纳 矩阵已知 节点注入 电流已知
I1 0, I 4 0
I 2 I3 0
I2
I3
导纳形式的节点方程
矩阵形式
Y11V1 Y12V2
Y1nVn I1 Y21V1 Y22V2 Y2 nVn I 2 ... Yn1V1 Yn 2V2 YnnVn I n
什么是“数学模型”：an example
• Electrical resistance