当前位置：文档之家 › MSA测量系统分析讲义kapa解读

MSA测量系统分析讲义kapa解读

  • 格式：ppt
  • 大小：645.00 KB
  • 文档页数：52

下载文档原格式

  / 52

合集下载

读懂MSA手册中Kappa分析的结果(IATF16949五大手册 测量系统分析)

读懂MSA手册中Kappa分析的结果(IATF16949五大手册 测量系统分析)

44，是A和B都评价150次，两 个人都认为不合格的次数
0 A
1
总计
B
0
1
观测值 44
6
期望值 15.7
34.3
观测值
3
97
期望值 31.3
68.7
观测值 47
103
期望值 47.0 103.0
总计
50 50.0 100 100.0 150 150.0
6，是A和B都评价 150次，A认为不合 格，而B认为合格
的次数
假设检验分析—交叉表法 评价人A与评价人B的交叉表
3，是A和B都评价150次，A认 为合格，B认为不合格的次数
0 A
1
总计
B
0
1
观测值 44
6
期望值 15.7
34.3
观测值
3
97
期望值 31.3
68.7
观测值 47
103
期望值 47.0 103.0
总计
50 50.0 100 100.0 150 150.0
期望是试验中每次可能结果的概率乘以其结果的总和 可以这样理解，当多次进行这样的试验，最终获得的结果就是期望值
期望的计算方法
简单例子：扔硬币，国徽向上获得1元，扔一次付出0.6元，那 么多次这样扔，收益多少？
计算：收益=获得—付出=0.5X1-0.6=-0.1元。这是赔钱的
假设检验分析—交叉表法
评价人A与评价人B的交叉表
假设检验分析—交叉表法
评价人A与评价人B的交叉表
这里15.7的期望值，通过评价人A、 B共同选择不合格的概率乘以评价
B
次数总获得计
0 A
1
总计
0

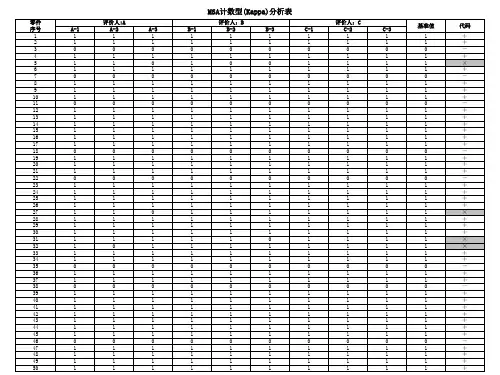
MSA计数型Kappa分析

MSA计数型Kappa分析

3
4.3
22.7
0
123
19.7 103.3
24
126
24.0 126.0
总计
27 27.0 123 123.0 150 150.0
Po 0.98
Pe 0.72
3，是评价人A 在150次判定中， A也认为不合格 的次数,基准值
不合格，
评价人A与基准交叉表数据分析
0，是评价人A在150次判定中，基 准值不合格，A也认为不合格的次
Po 0.98
Pe 0.72
3，是评价人A 在150次判定中， A认为合格的总 数,（0+123=123）
评价人A与基准交叉表数据分析
24，是基准总的不合格总数，不 合格8个，3次判定（8*3=24）
A与基准 交叉表
数量
0 期望数量
A
数量
1 期望数量
总计
数量 期望数量
基准值
0
1
24
3
4.3
22.7
1 期望数量
总计
数量 期望数量
基准值
0
1
24
3
4.3
22.7
0
123
19.7 103.3
24
126
24.0 126.0
总计 27 27.0 123 123.0 150 150.0
Po 0.98
Pe 0.72
KAPPA=（P0-Pe ）/ （n-Pe ） P0 =24+123
Pe =4.3+103.3 总评价次数：150
总计
27 27.0 123 123.0 150 150.0
总计
27 27.0 123 123.0 150

KAPPA【MSA】

KAPPA【MSA】

Minitab工具
Kappa计算也可以通过软件Minitab来实现 路径： 打开Minitab 软件－打开工作表－ 统计－质量工具－属性一致性分析.下表为 范例．
范例
１．打开工作表，选择kappa test excl.
2. 点击统计－质量工具－属性一致性分析
３．输入数据：属性列（Ｔ）为“判定值”，样本（Ｌ）为“样品”，检验 员（Ａ）为“检验员”
下表代表上表的数据，其中每个单元格 用总数的百分比来表示
Rater A First Measure Good Bad Rater A Second Measure
检验员A比例
代表10/20
Good Bad
0.5 0.05 0.55
0.1 0.35 0.45
0.6 0.4
由行和列的总和计算而得
计算检验员A的Kappa值
◆测试样品收集
在选择测试样品时，要考虑以下几方面：
如果只有两个类别：良品和次品，
◆至少应该选择20个良品和20个次品
最多可选择 50个良品和50个次品
尽量保持大约50%的良品和50%的次品
选择不同程度的良品和次品
如果样品类别超过2种，其中一类是优良，其它类别是不同 种类的缺陷方式 ◆至少应该选择大约50%的良品和每种缺陷方式最少为10%的
3第二格代表检验员a在第一次测量中判定一个样品为次品在第二次测量中判定为良品的次数第四格代表检验a在第一次测量和第二次测量中判定一个样品为次品的次数第三格代表检验员a在第一次测量中判定一个样品为良品在第二次测量中判定为次品的次数交叉表边格的数字代表行和列的总和交叉表比例检验员a比例下表代表上表的数据其中每个单元格用总数的百分比来表示代表1020由行和列的总和计算而得对kappa的定义将有所不同取决于我们是在定义检验员内部kappa还是在定义检验员之间的kappa计算检验员a的kappa值pobserved检验员两次判断一致比率检验员a两次一致判定为良品

MSA计数型测量系统分析-假设试验分析法(KAPPA)

MSA计数型测量系统分析-假设试验分析法(KAPPA)

B
0.954 Good
C
0.954 Good
测量系 统有效
评价人
零件总数 正确判断数 有效性% 结* 有论效性 = 正确
A
30 29 97% Good
B
30 29 97% Good
C
30 29 97% Good
评价人 的接受
漏发警报的比例
结论
误发警报的比例
A
0%
接受
1%
B
0%
接受
1%
* 漏C发警
0%
D
16
D
D
D
17
A
A
A
18
D
D
D
19
D
D
D
20
D
D
D
21
D
D
D
22
D
D
D
23
D
D
D
24
D
D
D
25
D
D
D
26
D
D
D
27
D
D
D
28
A
A
A
29
D
D
D
30
D
D
D
评价人之间数据报
A1*C1
A D D D D D D D A D D D D D D D A D D D D D D D D D D A D D
A2*C2
1
3
1
1
1
1
1
1
1
1
1
1
4
1
1
1
1
1
1
1
1
1

MSA计数型测量系统分析——假设试验分析法(Kappa)

MSA计数型测量系统分析——假设试验分析法(Kappa)

6.136.13 计数型测量系统分析计数型测量系统分析——————假设试验分析法假设试验分析法假设试验分析法（（Kappa Kappa））说明：参照张智勇所著《ISO/TS16949五大工具最新版一本通》（机械工业出版社）编写。

计数型测量系统的分析是为了确定不同班次，不同生产线的检查人员是否能正确地区分合格品和不合格品，分析出测量结果与标准值的符合程度，以及他们自身和相互之间重复检查的一致程度。

假设试验分析—交叉表法是一种常用的计数型测量系统分析方法。

交叉表法可以在基准值（分析用样品称为基准，用计量型测量系统对样品进行测量，测量值称为基准值）已知的情况下进行，也可以在基准值未知的情况下进行。

在基准值未知的情况下进行，可以评价测量人之间的一致性，但不能评价测量系统区分好与不好的能力。

在基准值已知的情况下，即可评价测量人之间的一致性，又能评价测量人员与基准值的一致性，以及测量的有效性、漏判率和误判率，从而判断出测量人区分合格和不合格零件的能力。

6.136.13.1 .1 .1 未知基准值的一致性分析未知基准值的一致性分析1）随机选取g=50（一般选取g=30～50个样本）个能够覆盖过程范围的零件，对这些零件进行编号。

零件的编号不要让测量人知道，但分析人应该知道。

2）由3名评价人以随机盲测的方式测量所有零件各m=3次，每人测量次数为n=g×m=50×3=150次。

“接受”记为“1”，“拒绝”记为“0”，将三人所测150×3=450个数据记录于表6-21中。

测量时应按这样的规则进行：先让A 测量人以随机顺序对50个零件进行第1轮测量，然后让B 测量人、C 测量人以随机顺序进行第1轮测量，再让A 测量人进行第2轮测量，以此类推，完成测量工作。

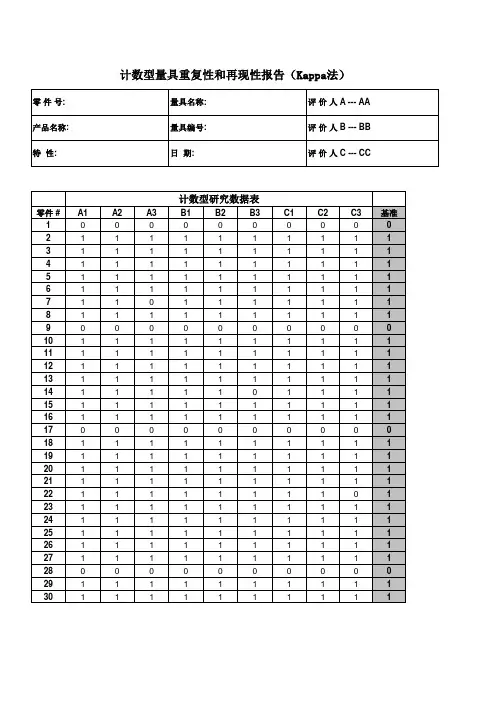
表6-21 计数型测量系统分析数据表零件测量人A 测量人B 测量人C基准基准值代码A-1 A-2 A-3 B-1 B-2 B-3 C-1 C-2 C-31 1 1 1 1 1 1 1 1 1 1 0.476 901 +2 1 1 1 1 1 1 1 1 1 1 0.509015 +3 0 0 0 0 0 0 0 0 0 0 0.576459 －4 0 0 0 0 0 0 0 0 0 0 0.566152 －5 0 0 0 0 0 0 0 0 0 0 0.57036 －6 1 1 0 1 1 0 1 0 0 1 0.544 951 ×7 1 1 1 1 1 1 1 0 1 1 0.465454 ×8 1 1 1 1 1 1 1 1 1 1 0.502295 +9 0 0 0 0 0 0 0 0 0 0 0.437817 －10 1 1 1 1 1 1 1 1 1 1 0.515573 +11 1 1 1 1 1 1 1 1 1 1 0.488905 +12 0 0 0 0 0 0 0 10 0 0.559918 ×13 1 1 1 1 1 1 1 1 1 1 0.542704 +14 1 1 0 1 1 1 1 0 0 1 0.454518 ×15 1 1 1 1 1 1 1 1 1 1 0.517377 +16 1 1 1 1 1 1 1 1 1 1 0.531939 +17 1 1 1 1 1 1 1 1 1 1 0.519694 +18 1 1 1 1 1 1 1 1 1 1 0.484167 +19 1 1 1 1 1 1 1 1 1 1 0.520496 +20 1 1 1 1 1 1 1 1 1 1 0.477236 +21 1 1 0 1 0 1 0 1 0 1 0.452310 ×22 0 0 1 0 1 0 1 10 0 0.545604 ×23 1 1 1 1 1 1 1 1 1 1 0.529065 +24 1 1 1 1 1 1 1 1 1 1 0.514192 +25 0 0 0 0 0 0 0 0 0 0 0.599581 －26 0 1 0 0 0 0 0 0 1 0 0.547204 ×27 1 1 1 1 1 1 1 1 1 1 0.502436 +28 1 1 1 1 1 1 1 1 1 1 0.521642 +29 1 1 1 1 1 1 1 1 1 1 0.523754 +30 0 0 0 0 0 1 0 0 0 0 0.561457 ×31 1 1 1 1 1 1 1 1 1 1 0.503091 +32 1 1 1 1 1 1 1 1 1 1 0.505850 +33 1 1 1 1 1 1 1 1 1 1 0.487613 +34 0 0 1 0 0 1 0 1 1 0 0.449696 ×35 1 1 1 1 1 1 1 1 1 1 0.498698 +36 1 1 0 1 1 1 1 0 1 1 0.543077 ×37 0 0 0 0 0 0 0 0 0 0 0.409238 －38 1 1 1 1 1 1 1 1 1 1 0.488184 +39 0 0 0 0 0 0 0 0 0 0 0.427687 －40 1 1 1 1 1 1 1 1 1 1 0.501132 +41 1 1 1 1 1 1 1 1 1 1 0.513779 +42 0 0 0 0 0 0 0 0 0 0 0.566575 －43 1 0 1 1 1 1 1 1 0 1 0.462410 ×44 1 1 1 1 1 1 1 1 1 1 0.470832 +45 0 0 0 0 0 0 0 0 0 0 0.412453 －46 1 1 1 1 1 1 1 1 1 1 0.493441 +47 1 1 1 1 1 1 1 1 1 1 0.486379 +48 0 0 0 0 0 0 0 0 0 0 0.587893 －49 1 1 1 1 1 1 1 1 1 1 0.483803 +50 0 0 0 0 0 0 0 0 0 0 0.446697 －3）根据表6-21中的0和l 数据的结果将评价人A 和B、B 和C、A 和C 利用交叉表方法进行统计（见表6-22），A*B 栏中“0*0”代表A、B 两人均判拒绝的次数，统计有44个；“0*1”代表A 判拒绝而B 判接受的次数，统计有6个；“1*0”代表A 判接受而B 判拒绝的次数，统计有3个；“1*1”代表AB 两人同时判为接受的次数，统计有97个，将统计结果依次填入表6-22中。

超详细MSA测量系统分析讲解

超详细MSA测量系统分析讲解
四.MSA的分析方法——（一）计量型测量系统
2.线性的分析方法和接受准则
●回顾：
1.什么是线性？
●线性指南
1.在量具的操作范围内，选择g（子组数）≥5个零件 2.检验每个零件，以确定基准值 3.一个人测量每个零件m（子组容量）≥10次 4.计算每次测量的零件偏倚及零件偏倚的平均值。（偏倚i，j=Xi，j -基准值） 5.在线性图上画出单值偏倚和基准的偏倚值 6.计算并画出最佳拟合线和置信带 7.画出“偏倚=0”线，评审该图指出特殊原因和线性的可接受性 （即“偏倚=0”线必须完全在拟合线置信带以内）
MSA
课前思考
1.什么是MSA ？ 2.什么时候做MSA？ 3.谁做MSA？ 4.哪些测量系统需要做MSA？ 5.在哪里做MSA？ 6.怎么做MSA？原理是什么？
MSA
第一单元
MSA的基本概念
MSA
二.MSA的基本概念
1.测量的定义
●测量：被定义为“对某具体事物赋予数字（或数值），以表示它们 对于特定特性之间的关系”。这定义由C.Eisenhart（1963）首次提出 。赋予数字的过程被定义为测量过程。而数值的指定被定义为测量值 。
3.MSA与FMEA（潜在失效模式及后果分析）
a. FMEA可以用来识别特殊特性，为SPC和MSA确定控制和分析的 对象
b.可以建立测量系统FMEA，管理测量系统的风险
MSA
一.MSA的概述介绍
（二）MSA 与汽车行业五大质量手册
4.MSA与SPC（统计过程控制）
测量系统对适当的数据分析来说是很关键的，在收集过 程数据之前就应很好地对它加以了解。这些测量系统缺少 统计控制，或它们的变差在过程总变差中占很大比例，就 可能做出不恰当的决定。

MSA第三版中KAPPA分析法精讲

0 0 C 1 43 17.0 8 34.0 51 51.0
Top Consulting
总计 7 33.0 92 66.0 99 99.0 50 50.0 100 100.0 150 150.0
A
1
总计
观测值 期望值 观测值 期望值 观测值 期望值
假设检验分析—交叉表方法



计算Kappa值 Kappa=（P0-Pe)/(n-Pe) 其中P0=对角线单元中观测值的总和； Pe=对角线单元中期望值的总和。 A与B的Kappa值 P0=44+97=141 Pe=15.7+68.7=84.4 Kappa=(141-84.4)/(150-84.4)=0.86
Top Consulting
风险分析法
数据收集 随机从过程中抽取50个零件样本，以获得覆盖过 程范围的零件。使用3名评价人，每位评价人 对每个零件评价3次，将评价结果记录在“计 数型研究数据表”中。1代表接受，0代表不接 受。参见附表。 评价的组织人员通过使用实验室设备等获得每个 零件的基准值，表中的“-”、“+”、“×”代 表零件处于I区、III区和II区。
50 39
系统有效得分与计数
50 39
64%
78%
64%
78%
89%

89%


结论：1 评价人自己在所有试验上都一致 2 评价人在所有试验上都与基准一致 3 所有评价人自己保持一致，两两间一致 4 所有评价人自己和两两间一致且与基准一致
Top Consulting
Top Consulting

A与B的交叉表
0 44 15.7 3 31.3 47 47.0
Top Consulting

KAPPA分析说明

KAPPA分析说明Kappa 评估说明：⽬的：评价【⽬视测量系统】的检出能⼒对象：从事产品外观检查的岗位⼈员，包括：品管QC、外观全检⼈员周期：新⼊或转岗⼈员培训合格后，在岗⼈员每季度⼀次；标准：《测量系统分析程序》（C0801-S10）《风险分析法（Kappa）分析报告》（FM-C0801-S10-03）制作评估样品（50pcs）：1.1 从量产中收集50个产品，不限产品型号，但须为相同⽣产⼯艺；其中有35个为不良品，不良类型需基本覆盖所有常发外观缺陷，缺陷程度不能太明显；1.2 将收集的样品交由品管⼯程师评判，将评判结果和缺陷内容按样品顺序进⾏记录，并对样品做好较隐秘的序号标记（1~50），必要时可使⽤特殊符号；样品序号状态参考值缺陷内容特殊符号1不合格0脏污⽩，⿇点XX… ………50合格1⽆2、评估准备：2.1 评估前，样品收集⼈对被评价⼈进⾏培训，明确产品外观缺陷的评判标准和接收准则；2.2 评估按检验⼯位开展，每次评价3位员⼯，被评价⼈已独⽴上岗并培训合格；不⾜3⼈时也可单独评价；2.3 三位被评价⼈依次完成50个样品的3次检查，累计产⽣150个检查结果，三次检查需交替或间隔⼀定时间后进⾏，确保“盲测”；2.4 需要⼀位数据记录员和⼀位标准判定⼈协助完成评估3、评估步骤：3.1 记录员在评估表上记录被评价⼈的基本信息，确认3位评估⼈的检查顺序（按⼈次交替进⾏）后，开始评估；3.2 记录员调整样品顺序，交由第⼀位被评价⼈检查，记录检查结果，判定正确记【√】，错误记【×】；当检查结果为不合格时，评价⼈告知缺陷内容和位置（若样品有多个缺陷，只要有⼀个缺陷描述正确，即判为正确）；3.3 重复步骤1.2，完成余下的8轮样品检查，记录检查结果；再将⼿⼯数据录⼊【kappa分析报告】，形成评估结果报告（合格由1表⽰，不合格由0表⽰）。

3.4 检查中如对样品缺陷有异议，由标准判定⼈评判4、评估结果（判定准则）：条件⼀：⼀致性（Kappa值）0.75＜Kappa≤1表⽰有很好的⼀致可接受0.4＜Kappa≤0.75表⽰⼀致性⼀般条件接受0＜Kappa≤0.4表⽰⼀致性不好不可接受条件⼆：有效性&漏判率&误判率结果有效性漏判率误判率备注可接受≥90%≤2%≤5%同时满⾜条件接受≥80%≤5%≤10%同时满⾜不可接受＜80%＞5%＞10%满⾜⼀个测量系统判定条件⼀和条件⼆同时为【可接受】，测量系统判为【可接受】条件⼀和条件⼆同时为【不可接受】，测量系统判为【不可接受】其他情形，测量系统判为【条件接受】，需明确限定条件5、结果应⽤：5.1 部门主管基于测量系统评估结果，更新员⼯的技能等级⽬视表；每季度定期评估后，再次更新技能等级⽬视表；5.2 评价结果为【不可接受】时，关联部门应暂停该测量系统的使⽤，并对已检测的产品进⾏追溯处理；并基于分析报告改进测量系统，如⼈员培训、检查⽅法调整、检查环境改善，必要时考虑调整被测⼈员的岗位安排；5.3评价结果为【条件接受】时，关联部门需采取措施持续改进。

测量系统分析(MSA)通用课件


稳定性
稳定性是衡量测量系统在长时间内保持一致性的参数。
稳定性分析通常涉及在一段时间内多次测量同一标准值，以检查测量系统的变化。 这种方法有助于确定测量系统是否随时间推移而发生变化，并评估其可靠性。
重复性和再现性
重复性和再现性是衡量测量系统在不 同操作者或不同条件下的一致性的参 数。
VS
重复性是指在相同条件下，同一操作 者多次测量的一致性。再现性则涉及 不同操作者或不同条件下测量的结果 是否一致。这些分析有助于评估测量 系统的可重复性和可再现性，并确定 其可靠性。
偏倚通常由校准曲线、线性回归分析或其它统计方法确定。 校准曲线是通过比较已知标准值和测量系统所得值来建立的。 线性回归分析则用于评估测量系统的准确性，并确定是否存 在系统误差。
线性
线性是衡量测量系统在预期范围内的 一致性和准确性的参数。
线性分析通过比较不同水平的已知标 准值与测量 系统所得值来进行。这种 方法有助于识别测量系统在高、中、 低值的一致性，并确定是否存在非线 性误差。
范围
确定分析所涉及的测量设备和操作人 员范围，以及需要分析的测量过程和 产品特性。
确定测量系统类型
测量设备
根据分析目的和范围，选择适当的测量设备，并了解其技术规格和性能参数。
操作人员
确定负责测量的人员，了解其资质、经验和培训情况。
制定分析计划
方法
选择适当的测量系统分析方满足要求。
案例二：重复性和再现性分析案例
总结词
本案例介绍了如何进行重复性和再现性分析，以评估 测量系统的精密度和可靠性。
详细描述
本案例通过实际数据展示了如何进行重复性和再现性 分析。首先，对同一实际样品进行多次测量，计算测 量结果的重复性。接着，对不同时间、不同操作者、 不同仪器条件下进行测量，计算再现性。最后，根据 分析结果判断测量系统是否满足要求。

计数型MSA：Kappa分析中“期望计数”的计算方法

计数型MSA：Kappa分析中“期望计数”的计算方法我们仍用MSA手册中的例子来做说明。

两评价人A和B分别对随机抽取的50个零件进行测量，对每个零件的测量随机地重复了3次。

设定1表示可接受的决定（即评为1类），0表示不可接受的决定（即评为0类）。

测量结果用以下交叉表列出。

科恩（Cohen）给出的Kappa计算公式为：MSA手册中定义P0为对角栏框中（观测）计数占总计数的比例，Pe为对角栏框中期望计数占总计数的比例。

（第三版中文MSA手册中翻译有误，这里是按英文版翻译过来的）（观测）计数容易理解，如对角栏框中的44表示A和B都评为0类的测量次数，97表示A 和B都评为1类的测量次数，而6则表示A评为0类但B评为1类的测量次数，3则表示A评为1类但B评为0类的测量次数。

因此，，P0也就是评价人A和B在测量中实际一致性的比率。

那期望计数是指什么呢？假如这两位评价人都是任意地（猜测）将50 个零件判定为可接受或不可接受，其结果也会达到一定程度的一致，不过这里的一致是偶然达到的，这种偶然达到的一致性比率称为偶然一致性比率，也就是Kappa计算中的Pe。

当评价人A 与B 随机地作评价时，此两人行动一定是独立的，互不影响，从而两人同评为0 类的概率为P0+×P+0，两人同评为1 类的概率为P1+×P+1。

（这里P0+表示A评价人评为0类的测量次数占总测量次数的比率，P1+表示A评价人评为1类的测量次数占总测量次数的比率；同理P+0、P+1分别表示B评价人评为0类的测量次数占总测量次数的比率，和B评价人评为1类的测量次数占总测量次数的比率。

这时偶然一致性比率Pe = P0+×P+0+ P1+×P+1。

因此，这里15.7和68.7分别就是两评价人同时评为0类和1类的期望计数，分别为对应单元格行总计数乘以列总计数除以总计数（即总测量次数）所得。

同样31.3和34.3这两个期望计数也是按同样方式得出的。

  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
3/52
3

分析方法： 对计数数据测量的测量系统，可采用小样法， 以及MSA第三版所建议的方法；标准允许使用任 何顾客不反对的方法。 计量数据也是采用标准允许使用任何顾客不 反对的方法（如均值极差、方差等方法）。 对于那些无法使用常规测量系统方法的测量 系统，需要和顾客沟通。
MSA培训教材
4/52
MSA—测量系统分析讲义
培训教材
MSA培训教材
1/52
1
0、相关定义
分析的原理： 当我们在跳动时，目标也许没有跳动，但测量 的结果也许是对方在动（如在火车上的人---）；测 量系统分析的目的是不要把测量系统的波动（如自 己的波动）当成过程的波动，造成基于数据的过程 控制为错误的行动。
目的： 要研究测量过程带来的测量误差是否 会导致基于测量的控制被误导。
定性评价的仪 器或量具、标准、操作、 方法、夹具、软件、人员、环境和假设的 集合；用来获得测量结果的整个过程。
S W I P E
标准 工件(如,零件) 仪器 人/程序 环境
MSA培训教材
8/52
8
分辨力、可读性、分辨率 √别名：最小的读数的单位、测量分辨率、刻度 限度或探测度 √由设计决定的固有特性 √测量或仪器输出的最小刻度单位 √总是以测量单位报告 √ 1：10经验法则 有效分辨率 √对于一个特定的应用，测量系统对过程变差的灵敏 性 √产生有用的测量输出信号的最小输入值 √总是以一个测量单位报告
12/52
12
一、测量系统所应具有之统计特性
1、测量系统必须处于统计控制中，这意味 着测量系统中的变差只能是由于普通原因 而不是由于特殊原因造成的。这可称为统 计稳定性 。 2、测量系统的变差必须比制造过程的变 差小 。 3、变差应小于公差带 。
MSA培训教材
13/52
13
4、测量精度应高于过程变差和公差带两
者中精度较高者，一般来说，测量精度 是过程变差和公差带两者中精度较高者 的十分之一 。 5、测量系统统计特性可能随被测项目的 改变而变化。若真的如此，则测量系统 的最大的变差应小于过程变差和公差带 两者中的较小者 。
MSA培训教材
14/52
14
二、标准
1、国家标准 2、第一级标准(连接国家标准和私人公 司、 科研机构等) 3、第二级标准(从第一级标准传递到第二级 标准) 4、工作标准(从第二级标准传递到工作标准)
发现哪种环境因素对测量系统有显著的影响，例如 温度、湿度等，以决定其使用之空间及环境 。 第二阶段的评定 目的是在验证一个测量系统一旦被认为是可行的， 应持续具有恰当的统计特性 。 常见的就是“量具R&R”是其中的一种型式 。
MSA培训教材
17/52
17
四、各项定义

v 量具: 任何用来获得测量结果的装置，包括用来测 量合格/不合格的装置 。 v 测量系统：用来获得表示产品或过程特性的数值 的系统，称之为测量系统。测量系统是与测量结果 有关的仪器、设备、软件、程序、操作人员、环境 的集合。 v 量具重复性：指同一个评价人，采用同一种测量 仪器，多次测量同一零件的同一特性时获得的测量 值（数据）的变差。
4
测量系统分析是一个过程
输入:SWIPE
测量系统 分析
输出: 测量数据
MSA培训教材
5/52
5
ＭＳＡ实施步骤
１、根据控制计划，针对被测量的特性选择适当的测量工具； ２、确定测量系统分析方法（计数／计量，大样／小样）； ３、确定要进行分析所需的样品容量（从一定容量大小的总体内选取以 保证ＭＳＡ的质量）； ４、确定为开展ＭＳＡ所需的时间（采集数据的时间有时会大于数据分 析的时间）； ５、选择并实施分析（事先策划的零件数、测量者、测量次数）； ６、分析结果； ７、接受还是拒收测量系统； ８、拒收，则可考虑更换合适的测量系统。
●再现性 √由不同的评价人使用同一个量具，测量一个零件的一个特性时产生的测量平 均值的变差。 √对于产品和过程条件，可能是评价人、环境（时间）或方法的误差。 √通常指A．Ｖ- 评价人变差 √系统间（条件）变差 √ASTM E456-96 包括重复性、实验室、环境及评价人影响
MSA培训教材
MSA培训教材
9/52
9
基准值

√人为规定的可接受值 √需要一个可操作的定义 √作为真值的替代
√物品的实际值 √未知的和不可知的
真值


MSA培训教材
10/52
10
位置变差 ● 准确度


√“接近”真值或可接受的基准值 √ASTM包括位置和宽度误差的影响 √测量的观测平均值和基准值之间的差异 √测量系统的系统误差分量 √偏倚随时间变化 √一个稳定的测量过程是关于位置的统计受控 √别名：漂移 √整个正常操作范围的偏倚改变 √整个操作规程范围的多个并且独立的偏倚误 √ 测量系统的系统误差分量
MSA培训教材
6/52
6
1、测量定义为赋值（或数）给具体事物以
表示它们之间关 于特定性的关系。赋值 过程定义为测量过程，而赋予的值定义为 测量值。 2、量具：任何用来获得测量结果的装置， 经常用来特指用 在车间的装置；包括通 过/不通过装置。
MSA培训教材
7/52
7
测量系统：是用来对被测特性定量测量或
MSA培训教材
2/52
2
测量系统分析的范围： 当确定测量系统分析的范围从标准的符 合性角度出发，需要将控计划上涉及的测量 系统纳入，包括对产品特性和过程特性进行 测量的系统（对进行初始能力研究和PPAP的 产品特性测量系统，需要进行MSA；对实施 SPC的测量系统需要进行MSA）；
MSA培训教材
MSA培训教材
15/52
15
三、测量系统的评定

测量系统的评定通常分为两个阶段，称为第一阶段 和第二阶段 第一阶段：明白该测量过程并确定该测量系统是否 满足我们的需要。第一阶段试验主要有二个目的 ： 确定该测量系统是否具有所需要的统计特性，此项 必须在使用前进行 。
MSA培训教材
16/52
16
● 偏倚

● 稳定性



●线A培训教材
11/52
11
宽度变差
●精密度 √重复读数彼此之间的“接近度” √测量系统的随机误差分量 ●重复性 √由一位评价人多次使用同一种测量仪器，测量同一零件的同一特性时获得的 测量变差 √在固定和规定的测量条件下连续（短期）试验变差 √通常指E．Ｖ．-设备变差 √仪器（量具）的能力或潜能 √系统内变差