直线,射线,线段的认识

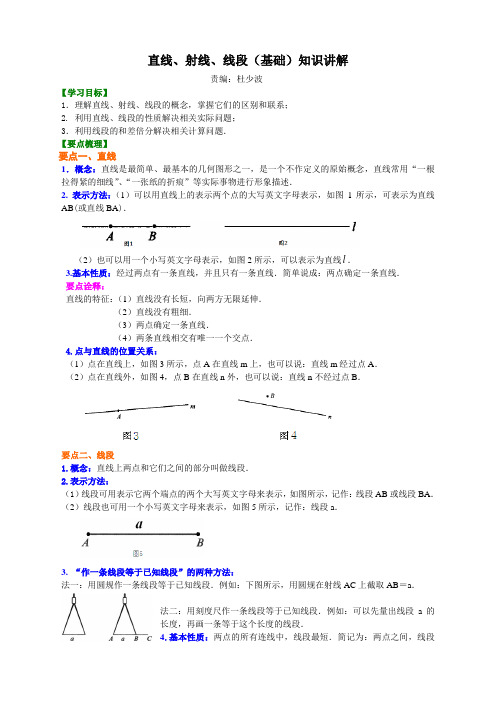
直线、射线、线段（基础）知识讲解责编：杜少波【学习目标】1．理解直线、射线、线段的概念，掌握它们的区别和联系；2. 利用直线、线段的性质解决相关实际问题；3．利用线段的和差倍分解决相关计算问题．【要点梳理】要点一、直线1．概念：直线是最简单、最基本的几何图形之一，是一个不作定义的原始概念，直线常用“一根拉得紧的细线”、“一张纸的折痕”等实际事物进行形象描述．2. 表示方法：（1）可以用直线上的表示两个点的大写英文字母表示，如图1所示，可表示为直线AB(或直线BA)．（2）也可以用一个小写英文字母表示，如图2所示，可以表示为直线l．3.基本性质：经过两点有一条直线，并且只有一条直线．简单说成：两点确定一条直线．要点诠释：直线的特征：（1）直线没有长短，向两方无限延伸．（2）直线没有粗细．（3）两点确定一条直线．（4）两条直线相交有唯一一个交点．4.点与直线的位置关系：（1）点在直线上，如图3所示，点A在直线m上，也可以说：直线m经过点A．（2）点在直线外，如图4，点B在直线n外，也可以说：直线n不经过点B．要点二、线段1.概念：直线上两点和它们之间的部分叫做线段．2.表示方法：（1）线段可用表示它两个端点的两个大写英文字母来表示，如图所示，记作：线段AB或线段BA．（2）线段也可用一个小写英文字母来表示，如图5所示，记作：线段a．3. “作一条线段等于已知线段”的两种方法：法一：用圆规作一条线段等于已知线段．例如：下图所示，用圆规在射线AC上截取AB＝a．法二：用刻度尺作一条线段等于已知线段．例如：可以先量出线段a的长度，再画一条等于这个长度的线段．4.基本性质：两点的所有连线中，线段最短．简记为：两点之间，线段最短．如图6所示，在A ，B 两点所连的线中，线段AB 的长度是最短的．要点诠释：（1）线段是直的，它有两个端点，它的长度是有限的，可以度量，可以比较长短．（2）连接两点间的线段的长度，叫做这两点的距离． （3）线段的比较：①度量法：用刻度尺量出两条线段的长度，再比较长短．②叠合法：利用直尺和圆规把线段放在同一条直线上，使其中一个端点重合，另一个端点位于重合端点同侧，根据另一端点与重合端点的远近来比较长短．5.线段的中点：把一条线段分成两条相等线段的点，叫做线段的中点．如图7所示，点C 是线段AB 的中点，则12AC CB AB ==，或AB ＝2AC ＝2BC ．要点诠释：若点C 是线段AB 的中点，则点C 一定在线段AB 上．要点三、射线1.概念：直线上一点和它一侧的部分叫射线，这个点叫射线的端点．如图8所示，直线l 上点O 和它一旁的部分是一条射线，点O 是端点．l2.特征：是直的，有一个端点，不可以度量，不可以比较长短，无限长．3.表示方法：（1）可以用两个大写英文字母表示，其中一个是射线的端点，另一个是射线上除端点外的任意一点，端点写在前面，如图8所示，可记为射线OA ．（2）也可以用一个小写英文字母表示，如图8所示，射线OA 可记为射线l ． 要点诠释：(1)端点相同，而延伸方向不同，表示不同的射线．如图9中射线OA ，射线OB 是不同的射线．(2)端点相同且延伸方向也相同的射线，表示同一条射线．如图10中射线OA 、射线OB 、射线OC 都表示同一条射线．要点四、直线、射线、线段的区别与联系1.直线、射线、线段之间的联系（1）射线和线段都是直线上的一部分，即整体与部分的关系．在直线上任取一点，则可将直线分成两条射线；在直线上取两点，则可将直线分为一条线段和四条射线．（2）将射线反向延伸就可得到直线；将线段一方延伸就得到射线；将线段向两方延伸就得到直线． 图6 图7图8 图9 图102．三者的区别如下表要点诠释：（1）联系与区别可表示如下：（2）在表示直线、射线与线段时，勿忘在字母的前面写上“直线”“射线”“线段”字样．【典型例题】类型一、相关概念1.下列说法中，正确的是( )A．射线OA与射线AO是同一条射线B．线段AB与线段BA是同一条线段C．过一点只能画一条直线D．三条直线两两相交，必有三个交点【答案】B【解析】射线OA的端点是O，射线AO的端点是A，所以射线OA与射线AO不是同一条射线，故A 错误；过一点能画无数条直线，所以C错误；三条直线两两相交，有三个交点或一个交点(三条直线相交于一点时)，所以D错误；线段AB与线段BA是同一条线段，所以B正确．【总结升华】直线和线段用两个大写字母表示时，与字母的前后顺序无关，但射线必须是表示端点的字母写在前面，不能互换．举一反三：【变式1】以下说法中正确的是（）A．延长线段AB到C B．延长射线ABC．直线AB的端点之一是A D．延长射线OA到C【答案】A【变式2】如图所示，请分别指出图中的线段、射线和直线的条数，并把它们分别表示出来.【答案】解：如下图所示，在直线上点A左侧和点C右侧分别任取点X和Y.图中有6条射线：射线AX、射线AY、射线BX、射线BY、射线CX、射线CY.有3条线段：线段AB(或BA)、线段BC(或CB)、线段AC(或CA)有1条直线：直线AC(或AB，BC).类型二、有关作图2．如图所示，线段a，b，且a＞b．用圆规和直尺画线段：(1)a+b；(2)a-b．【答案与解析】解：(1) 画法如图(1)，画直线AF，在直线AF上画线段AB＝a，再在AB的延长线上画线段BC＝b，线段AC就是a与b的和，记作AC＝a+b．(2) 画法如图(2)，画直线AF，在直线AF上画线段AB＝a，再在线段AB上画线段BD＝b，线段AD 就是a与b的差，记作AD＝a-b．【总结升华】在画线段时，为使结果更准确，一般用直尺画直线，用圆规量取线段的长度．举一反三：【变式1】如图，C是线段AB外一点，按要求画图：（1）画射线CB；（2）反向延长线段AB；（3）连接AC，并延长AC至点D，使CD=AC．【答案】解：【高清课堂：直线、射线、线段397363 按语句画图3（3）】【变式2】用直尺作图：P 是直线a 外一点，过点P 有一条线段b 与直线a 不相交.【答案】解：类型三、有关条数及长度的计算3.如图，A 、B 、C 、D 为平面内任意三点都不在同一条直线上的四点，那么过其中两点，可画出 条直线.【思路点拨】根据两点确定一条直线即可计算出直线的条数．【答案】6条直线【解析】由两点确定一条直线知，点A 与B,C,D 三点各确定一条直线，同理点B 与C 、D 各确定一条直线，C 与D 确定一条直线，综上：共有直线：3+2+1=6（条）.【总结升华】平面上有n 个点，其中任意三点不在一条直线上，则最多确定的直线条数为：(1)123...(1)2n n n -++++-=． 举一反三：【变式1】如图所示，已知线段AB 上有三个定点C 、D 、E ．(1)图中共有几条线段？(2)如果在线段CD 上增加一点，则增加了几条线段？你能从中发现什么规律吗？【答案】解：(1)线段的条数：4＋3＋2＋1＝10(条)；(2)如果在线段CD 上增加一点P ，则P 与其它五个点各组成一条线段，因此，增加了5条线段. （注解：若在线段AB 上增加一点，则增加2条线段，此时线段总条数为1＋2；若再增加一点，则又增加了3条线段，此时线段总条数为1＋2＋3；…；当线段AB 上增加到n 个点(即增加n －2个点)时，线段的总条数为1＋2＋……＋(n －1)＝21n(n －1) .） 【变式2】)如图直线m 上有4个点A 、B 、C 、D ，则图中共有________条射线．【答案】84.（2016春•启东市月考）已知点C 在线段AB 上，线段AC=7cm ，BC=5cm ，点M 、N 分别是AC 、BC 的中点，求MN 的长度．【思路点拨】根据M 、N 分别为AC 、BC 的中点，根据AC 、BC 的长求出MC 与CN 的长，由MC+CN 求出MN 的长即可．【答案与解析】解：∵AC=7cm ，BC=5cm ，点M 、N 分别是AC 、BC 的中点，∴MC=AC=3.5cm ，CN=BC=2.5cm ，则MN=MC+CN=3.5+2.5=6（cm ）．【总结升华】此题考查了线段的和差，熟练掌握线段中点定义是解本题的关键．【高清课堂：直线、射线、线段397363画图计算例2】举一反三：【变式】在直线l 上按指定方向依次取点A 、B 、C 、D ，且使AB ：BC ：CD=2：3：4，如图所示，若AB 的中点M 与CD 的中点N 的距离是15cm ，求AB 的长.【答案】解：依题意，设AB ＝2x cm ，那么BC ＝3x cm ，CD ＝4x cm ．则有：MN=BM+BC+CN= x+3x+2x=15 解得：52x = 所以AB=2x =5252⨯=cm. 类型四、最短问题5.（2015•新疆）如图所示，某同学的家在A 处，星期日他到书店去买书，想尽快赶到书店，请你帮助他选择一条最近的路线（ ）A ．A →C →D →B B ． A →C →F →BC ． A →C →E →F →BD ．A →C →M →B【答案】B ．【解析】根据两点之间的线段最短，可得C、B两点之间的最短距离是线段CB的长度，所以想尽快赶到书店，一条最近的路线是：A→C→F→B．【总结升华】“两点之间线段最短”在实际生活中有广泛的应用，此类问题要与线段的性质联系起来，这里线段最短是指线段的长度最短，连接两点的线段的长度叫做两点间的距离，线段是图形，线段长度是数值．举一反三：【变式】 (1)如图1所示，把原来弯曲的河道改直，A、B两地间的河道长度有什么变化?(2)如图2，公园里设计了曲折迂回的桥，这样做对游人观赏湖面风光有什么影响?与修一座直的桥相比，这样做是否增加了游人在桥上行走的路程?说出上述问题中的道理．【答案】解：(1)河道的长度变小了．(2)由于“两点之间，线段最短”，这样做增加了游人在桥上行走的路程，有利于游人更好地观赏湖面风光，起到“休闲”的作用．。

第一册线段射线直线简介在几何学中，线段、射线和直线是基本的几何概念。

它们用于描述平面上的几何形状和位置关系。

本文将介绍线段、射线和直线的定义、特征和性质。

一、线段线段是由两个不同的点A和B确定的一段连续的直线部分。

线段AB通常记作A B。

线段有以下特征和性质：1.线段的长度可以通过求解点A和点B之间的距离来计算。

2.线段没有方向，即AB和BA表示同一个线段。

3.线段是有限的，它有一个起点A和一个终点B。

二、射线射线由一个起点A和一个方向确定。

射线上的点可以延伸到无穷远。

射线通常记作⃛AB。

射线有以下特征和性质：1.射线的长度没有限制，它可以一直延伸到无穷远。

2.射线有一个起点A，但没有终点。

3.射线的方向由起点指向延伸的方向。

三、直线直线是由两个以上的点确定的一条无限延伸的直线。

直线通常记作⟶AB或AB。

直线有以下特征和性质：1.直线是无限延伸的，它没有起点和终点。

2.直线上的任意两点之间的距离是相等的。

3.直线上的任意两点可以作为起点和终点来定义一个线段。

四、线段、射线和直线的关系线段、射线和直线都是由点所确定的，它们之间存在一定的关系。

1.线段是有限的，它有起点和终点。

射线和直线是无限延伸的，它们没有终点。

2.射线和直线可以视为特殊的线段，即线段的终点无限延伸得到射线，直线则是将线段的终点和起点都无限延伸得到的。

3.如果一个直线上有三个点A、B、C，且B A+A C̅=B C̅成立，则点A在线段BC 上，如果B A+A C̅>B C̅成立，则点A在射线BC上。

结论线段、射线和直线是几何学中基本的概念，它们用于描述平面上的形状和位置关系。

线段是有限的，有起点和终点；射线是无限延伸的，有起点但没有终点；直线是无限延伸的，既没有起点也没有终点。

线段、射线和直线在几何学中有着重要的地位，它们为我们研究平面几何提供了基础。

以上是关于第一册线段射线直线的简介和基本特征。

通过对这些概念的理解和运用，我们可以更深入地研究平面几何学，并应用于实际问题中的求解和分析过程中。

《直线、射线、线段》知识全解
课标要求
理解直线线段射线的概念及表示方法，区别它们之间的相同点与不同点，理解公理两点之间线段最短．
教材从线段的应用实例开始学习，提出直线、射线、线段表示方法，特性，点与直线的位置关系．在画图的过程中总结直线性质．本节学习的重点是线段，通过多种不同的方法比较线段的大小、引出中点的定义，两点的距离以及线段的性质．
内容解析
(1)直线、射线、线段的特性
端点数延伸性能否度量画法表示
线段2个不延伸可度量
线段AB、线段
BA
线段a
射线1个
向一个方向
无限延伸不可度量
射线OA
直线无端点
向两个方向
无限延伸
不可度量
直线AB(直线
BA)
直线l
(2)
经过两点有一条直线，并且只有一条直线，也就是“两点确定一条直线”．
(3)线段的性质
两点之间，线段最短．
(4)两点的距离：连接两点间的线段的长度．
(5)线段的中点：在线段上，把线段分成两条相等线段的点．
重点难点
本节内容的重点是理解直线性质，会用字母表示图形和根据语言描述图形，画一条线段，比较两条线段的长短，在现实情境中了解线段的性质．难点是根据语言描述画出图形，尺规作图．
教法导引
从学生已有的知识出发，激发学生的兴趣，利用小组交流、讨论的方式将问题解释清楚．学法建议
按照思考、交流、总结、应用的步骤学习．。

直线射线和线段的认识与运用直线、射线和线段是几何学中常见的概念，它们在各种问题与应用中都有重要的作用。

本文将介绍直线、射线和线段的定义及其在几何学中的运用。

一、直线直线是几何学中最基本的概念之一。

直线可看作是由无数个点按照一条延伸的路径排列而成。

直线的特点是无限延伸，没有起点或终点。

在几何学中，直线通常用字母表示，例如用字母l、m或AB等表示一条直线。

二、射线射线是由一个固定点开始，无限延伸的线段。

射线的起点称为起点，没有终点。

射线的延伸方向可以用一个箭头来表示。

通常，射线也用字母或者起点确定的一个向量来表示，例如用字母AB表示一条射线，其中A为起点，B为延伸方向上的一点。

三、线段线段是由两个点之间的所有点组成的线段，它具有起点和终点。

线段的长度是有限的，不会无限延伸。

在几何学中，线段通常用两个点的名字表示，例如用AB表示一条线段，其中A为起点，B为终点。

四、直线、射线和线段的运用直线、射线和线段在几何学中有广泛的应用，下面将简单介绍其中的一些应用。

1. 直线的应用直线的基本性质是它无限延伸，可以由两个点确定一条唯一的直线。

在实际生活中，直线的应用非常广泛，例如建筑物的竖直墙壁、道路的直线段等。

2. 射线的应用射线有一个起点和一个无限延伸的方向，可表示光线、矢量等概念。

在物理学和光学中，射线常用于描述物体的光学特性和光线的传播方向。

3. 线段的应用线段具有有限长度，常用于测量和描述物体的一部分。

在几何学中，线段是最基本的测量单位之一，也常用于描述物体的大小和位置关系。

总结：直线、射线和线段是几何学中常见的概念，它们各自具有不同的特点和运用方式。

直线无限延伸，射线有一个起点无限延伸，线段有有限的长度。

在问题和应用中，我们可以根据具体的情况选择合适的概念来描述和解决问题。

对直线、射线和线段的认识与运用的熟练程度，对于几何学及其应用领域的学习和理解都具有重要的意义。

人教版七年级数学上册直线射线线段知识
点
1.直线：一根拉得很紧的线，就给我们以直线的形象，直线是直的，并且是向两方无限延伸的。

一条直线可以用一个小写字母表示，如直线l;
2.射线：直线上一点和它一旁的部分叫做射线。

这个点叫做射线的端点。

一条射线可以用端点和射线上另一点来表示,如射线l或射线OA;
3.线段：直线上两个点和它们之间的部分叫做线段，这两个点叫做线段的端点。

一条线段可用它的端点的两个大写字母来表示，如线段AB;
4.(1)线和射线无长度，线段有长度;
(2)直线无端点，射线有一个端点，线段有两个端点。

精品小编为大家提供的直线射线线段知识点大家仔细阅读了吗?最后祝同学们学习进步。

人教版七年级上册数学第三章知识点（精编）
人教版七年级上册数学实际问题与一元一次方程知识点总结。

直线射线与线段的认识直线、射线和线段是几何学中的基本概念，对于理解空间关系和解决几何问题起着关键作用。

本文将从定义、特点及示例等方面论述直线、射线与线段的认识。

一、直线的认识直线是几何学中最基本的图形，它没有起点和终点，可以无限延伸。

直线可以用两个点来确定。

根据定义，直线上的任意两点都可以用线段连接起来。

直线的特点包括以下几个方面：1. 无限延伸性：直线可以无限延伸，既可以向左，也可以向右。

2. 独一性：通过两个不同的点，可以有且只有一条直线。

3. 无宽度：直线是没有宽度的一维图形，只有长度。

4. 反方向：直线没有方向，但可以通过箭头表示一个方向。

示例：通过两点A和B可以确定一条直线AB。

二、射线的认识射线是具有一个起点，但是没有终点的一条线段。

射线可以看作是由一个起点出发，向一个特定方向无限延伸的线段。

射线的特点包括以下几个方面：1. 有一个起点：射线始于一个唯一的起点。

2. 无终点：射线没有终点，可以无限延伸。

3. 方向性：射线只有一个特定的方向。

示例：以点A为起点，延伸至无限远的线段可以表示为射线AB。

三、线段的认识线段是由两个点A、B确定的一段有限长度的直线。

线段的特点包括以下几个方面：1. 有两个端点：线段有且只有两个特定的端点。

2. 有确定的长度：线段有一个确定的长度，可以通过两个端点的距离来表示。

3. 直线连结：线段是直线上的一部分，它的两个端点可以通过直线连接。

示例：由点A、B确定的线段可以表示为AB。

综上所述，直线、射线和线段是几何学中基本的概念。

直线没有起点和终点，可以无限延伸；射线有一个起点但没有终点，只能延伸；线段由两个点确定，有确定的长度。

了解并正确运用直线、射线和线段的概念，将有助于我们更好地理解和解决几何问题。

初步认识几何形线段直线和射线几何形线段、直线和射线是初步学习几何学时经常接触的概念。

在开始探究这些概念之前，我们需要先了解它们的定义和特点。

本文将介绍线段、直线和射线的基本概念，以及它们在几何学中的应用。

线段是指由两个端点确定的一段直线。

线段的长度是由起点和终点之间的直线距离来表示的。

我们可以用一条带箭头的线段表示，箭头表示线段的方向。

直线是由无数个点连成的一条无限延伸的路径。

直线没有起点和终点，可以无限延伸。

在几何学中，直线通常用一条没有箭头的直线表示。

射线是一条有一个起点，但没有终点的路径。

射线可以无限延伸到一个方向，一般用一条从起点开始的带箭头的线表示。

箭头表示射线的延伸方向。

线段、直线和射线在几何学中具有不同的特点和应用。

首先，线段在几何学中有着重要的作用。

它们被广泛用于测量和计算长度。

我们可以使用线段的长度来比较不同线段的大小，并进行相应的运算。

线段还可以用于构造几何图形，如多边形和圆等。

线段也是构建平面和立体几何体的基本元素。

接下来，直线是几何学中最基本的图形之一。

直线具有无限延伸的特点，它们可以连接两个点，也可以连接多个点。

直线在建筑、工程和设计等领域中有着广泛的应用。

在平面几何中，直线可以用来构建角度、切割几何图形，以及描述平行和垂直关系等。

最后，射线是几何学中的特殊线段。

射线有一个起点，但没有终点，可以无限延伸。

射线可以用来表示传输路径、发射角度等。

它们在物理学和光学等科学领域中有着重要的应用。

射线也是几何图形中的一种特殊构成元素，可以用来构建角度、切割几何图形等。

综上所述，线段、直线和射线是几何学中的基本概念。

它们在几何学研究、实际测量和工程设计等方面具有重要的作用。

熟练掌握线段、直线和射线的特点和应用，对于进一步学习和理解几何学以及应用数学都有着重要的意义。

希望通过本文的介绍，读者对线段、直线和射线有了初步认识，并能够更好地理解和应用它们在几何学中的各种概念和定理。