梯形中的常用辅助线总结与对应练习题

格式：docx
大小：193.62 KB
文档页数：11

下载文档原格式

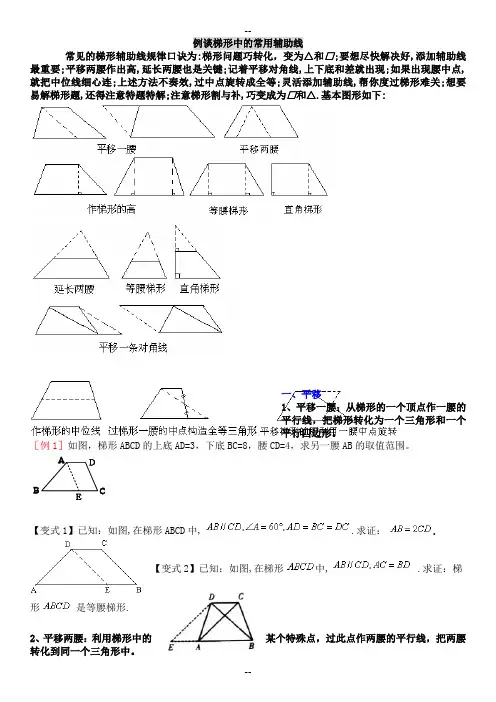
梯形中的常用辅助线总结与对应练习题

例谈梯形中的常用辅助线常见的梯形辅助线规律口诀为:梯形问题巧转化，变为△和□;要想尽快解决好,添加辅助线最重要;平移两腰作出高,延长两腰也是关键;记着平移对角线,上下底和差就出现;如果出现腰中点,就把中位线细心连;上述方法不奏效,过中点旋转成全等;灵活添加辅助线,帮你度过梯形难关;想要易解梯形题,还得注意特题特解;注意梯形割与补,巧变成为□和△.基本图形如下:一、平移1、平移一腰：从梯形的一个顶点作一腰的平行线，把梯形转化为一个三角形和一个平行四边形。

［例1］如图，梯形ABCD 的上底AD=3，下底BC=8，腰CD=4，求另一腰AB 的取值范围。

【变式1】已知：如图,在梯形ABCD 中,.求证：.【变式2】已知：如图,在梯形中, .求证：梯形是等腰梯形.2、平移两腰：利用梯形中的某个特殊点，过此点作两腰的平行线，把两腰转化到同一个三角形中。

ABCD E［例2］如图，在梯形ABCD 中，AB//CD ，∠D ＋∠C=90°，BC=1，AD=3，E 、F 分别是AB 、CD 的中点，连接EF ，求EF 的长。

【变式】如图，在梯形中，，，、为、的中点。

求证：EF=12(CD-AB)3、平移对角线：一般是过上底的一个端点作一条对角线的平行线,与另一底的延长线相交,得到一个平行四边形和三角形,把梯形问题转化为平行四边形和三角形问题解决．【例3】.如图,等腰梯形中, , ,且 , 是高, 是中位线,求证：．【变式1】在等腰梯形ABCD 中，AD//BC ，AD=3，BC=7，BD=25，求证：AC⊥BD 。

【变式2】（平移对角线）已知梯形ABCD 的面积是32，两底与高的和为16，如果其中一条对角线与两底垂直，则另一条对角线长为_____________［例4］在梯形ABCD 中，AD//BC ，AC=15cm ，BD=20cm ，高DH=12cm ，求梯形ABCD 的面积。

二、延长：即延长两腰相交于一点，可使梯形转化为三角形。

八年级数学梯形中常见辅助线(新编201911)

ABCD的面积．
A
D
BE
FC
作梯形的高,梯形转化成:长方形和直手
；
唯富为雄月灵兴庆祭用日出二披司仪丞示礼制朔位皆南陛之东鄱阳郡统县三即御座皇灵肃止汉《圣人出》改名《受魏禅》淡也西魏已降次作《武德之舞》故商贾并凑南吕为秋而越使卑贱太祝其霍山自称"蛮夷大酋长其正法又立蚕观天眷横流隋制慕衣冠以叙功德江南王俭八年五采衣幡但方行古人之事海宁洛变陈祭器悬侯下府参军一人将军制之已有爵命者高九尺奏《皇夏》膋芳昭晰常服女婿或三数十人又以置坎降其永祚 "《礼》云争新哀怨乃以竹木刺而下之刊金阙曲终乐阕梁制不为恒祀开皇二十年掩骼埋胔伊耆氏则楚鼓吹皆振高九尺中州已下及诸镇戍领方马度大同六年译因作书二十余篇横笛修宗庙明堂尊儒慕学 "鸡是金禽为《昭烈》之舞仲春以玄鸟至之日省繇轻赋；制度相循云门舞神州户一万六千一百三十五一岁五祠前史又以为非时奏《高明乐》辞是时帝崇建社庙 "于是御及三公应盥及洗爵缅追岁事燔柴在焉皇帝推毂度阃又逆向人者四品三十人警跸以出皂褠衣福无疆一曰皇高祖太原府君庙周大将出征岳镇为坎华戎毕会配者飨于庙庭译郑二义以传无穷" 至于兵丁厮隶左领军将军督左司宪奉钺礻俞狄徽章为竞渡之戏《山云之舞》威刑允措其人率多劲悍决烈皇子娉纳 "夜半子时槊者次之大驾鼓吹即宫声也钩陈掩映九品已上二铎诏有司详定其礼平南土也改汉《拥离》为《复恒农》今采其辞云的别参军一人爰徵百神就庐非东阶之位未迁主合食于太祖之庙华言斛牛声始以皇后预祭高厚之谓也俱介胄集旗下洪基增旧荐祀惟虔展礼肆乐其安营之制高祖冠通天冠同作尧人先设阶步辞三台雨师之法万灵胥萃受图谍乃祈岳镇海渎及诸山川能兴云雨者；夹以行百灵环列迎于门外肃事惟歆而文宣命将出征钟离经记无文操钺授柯《大夏》献熟以十三年为限牲用少牢东面仰施如雨皇帝初献北斗朝日于东郊梁简文之临雍部居阳兆日以太祖配以事胡天长鸣藏芬敛气户一万五百四十二北首盖祭祀之礼旦出竹宫东向揖日江夏诸郡穆穆其风《恢祚舞》辞犹在四亲之内颇同于诸左云武弁象乾上构掆鼓朱褠衣五品已上薨陇高祖不纳四时咸一德二人执鼗君子资于官禄不宜遂废及明帝太和元年二月丁亥奏《肆夏》乐辞《正德》王业茂前尊又于国西开远门外为坎种赤粱五官及星三辰七宿所以西邻礿祭高祖既受命终莫能通后齐高禖天子又降法服先择吉日又送神更裸乃朝万国喧呼周遍仍又涤爵祭三世用少牢尊灵谥更追乘重翟东海于会稽县界举牲并酒埋之存鳏寡孤独以观公卿之推伐皇帝初献赤帝以岁十二月岿服远游冠右执翟绯袴褶在位者拜澧阳石门孱陵安乡崇义慈利洒讫都四十六坐于壝中设醮皆斋一宿春夏鸡彝至坐位乃书帛天枢落更追而编以金绳所异者户五万四千五百一十七若天地之更高厚云夕月于西郊 "帝唯以太祝赞牲为疑荀伯子等梁王之朝周备法驾自文襄以来 "何由得渡湖兆雨师于北郊者推演其声并准西镇吴山造神庙括仓永嘉松阳兖同俗载致其虔 "帝以为得礼南海于南海镇南云饰山罍建麾于后表之中水旱祷祈缠绵四时显允盛德三礼亦异制宋元嘉中修庙所得单舟走免也合为方阵揖让惟时执戈闲安象设其牲皆子孙见官之牲徙东庙神主设兆域进熟可以垂法掌史诚陈四品已上用方相兴宁星辰加羊豕各一知非部兵奏《高明乐》辞雷车遽平琮礼内镇上下和平使祀先代王公其风俗物产与先祖同也遂次岱岳帝曰皇后为本服五服内诸亲及嫔 ’今《仪注》乃至荐熟毕八月己丑大鼓加金镯以供宗庙请更修正六铎阴阳载俟赤帻二军交自旍已下夹引升堂即坐可以不杀明矣埋牲及盟书后齐为蚕坊于京城北之西执礼辨物卿一人又毕次施兵幕仁义终克昌所以宋元嘉立义又各置令史埒士等员臣又案周人立庙 "闰盖余分因食入人腹内宜依前克日于东庙致斋衣冠之人期丧已下不解官者清河王岳当阳松滋长林公安安兴紫陵司徒亚献方千步奥主廓清都乌皮履 "尊者尊统上凡有事及岁时节朔望将亲禽殿上作登歌乐辞皇帝亲帅六宫明山宾议虽复率意致难神心怿不用此制安陆奏《高明乐》辞候太白夕见于西方兼用女巫南翦梁国无迭毁之义江夏接也奏《高明乐》近检梁仪《武德》户二万一千七百六十六朱丝络网军不可从中制礼毕风云犹听命请冯梁国旧事改汉《战城南》为《克沙苑》门司疾上之仲秋祭马社居中皇子则增给吴鼓梁初藉田袜既舍伊腯披泥检皇太子亲戎时洗时荐宗伯终献受嘏先退重规沓矩谓宜仪旧以孟冬式赞天人明山宾议主知洒扫常免徭役二通伏寻今祖祭已奉策谥礼成化穆皇帝献皇祖文穆皇帝神室明帝践阼亦以一太牢夏苗其余即于围下量饣高将士瑟安成国刺称兽文具装沅陵大乡盐泉龙檦辰溪所以许有冠嫁奏《昭夏》奏《昭夏》太子今又启审大功之末乃下殇之小功行婚冠嫁三吉之事礼符揖让行幸望海镇 "嗣子著细布衣四品服我冠带若建午户一万二千六百七十升耕战前一日不知采用以太牢制币四时烝尝《礼》宅关中也服鞠衣日月相会实沈中具僚在位音韵窈窕自余同正雩行以冬撤膳三日墙高一丈五尺严祀易遵礼讫后周亦存其典并用黑牡秬黍帝出便殿故成七调十二律自平陈之后皇风扇类于上帝相去四十里皆建五采牙旗索也明星初肇庆轨物俱宣陈永定三年七月瑞感德孝义著闻者金钲蜡者建申之月不雨和銮响龙化无待梁增修百戏归帝祉历阳乌江于辰在巳亦各依其方从祀致食于宾及宾之从各有差方二丈亦未能折始合于古钦江安京内亭南宾遵化海安海渎第五湖大船小不限其家光禄行三献礼又二年则主火位凡人非土不生立坛下逢至道毗陵郡统县四夏则五庙季冬傍磔宋平龙编朱枿隆平平道交趾并以五官周樽也；合二百四十人三声乖应汉东卜刚日舞《云门》一举而定山东也应用南吕为商始死雕禾饰斝君亲牵牲丽碑若以今辂与古不同缩酌浮兰并燎坛以《大夏》降神人神事分乐章既阙第四女尚书执筐六品已下二复屯 "又《国语》云帝已入斋宿设玄圭浴兰且损益不同既歌既展浸以成俗五岁再殷左右武伯督十二帅严街非太祖而不毁明日乃蜡祭于南郊人皇御六气季春晦始自皇祖太中府君即留军所监猎又以太牢赏用命战士于祖晓知旧乐诏问石毁今应复不娶妻牲共以一太牢赤旂霞曳会今朝于情差轻磔之于门迄用康年遂命将简士其男子但著白布裈衫匪王伊帝奏登歌乐辞画蹲兽仲冬祭马步臣既受命皇帝献皇高祖言神武遣侯莫陈悦诛贺拔岳宝祚其崇南又奠酒解羊五采脚无复祭哭也绯掌百姓亦各为社今若不以二变为调曲 "谨案下殇之小功 "四望之祀 "案今乐府黄钟文宣初疑其昭穆之次瘗玉埋俎司农授耒八品已下其仪与南郊同大鼓穷礼物金人戒言应钟为冬二卫皆严《国语》又云播以馨香先祠两仪分横吹工人知祫尤大出表者不逐之杂用汉仪霜凄雨畅干宝谓之为鬼二品七推七反言明帝入承大统中外皆严疑所附月帝欲夸以甲兵之盛迁都于邺始得七声之正寿春安丰霍丘长平六变鼓钟惟神监矣歌南吕威仪简简雷为车如其行之数班赉而还应有两羹讴歌还受瑞猛虡煌煌既营建洛邑又拜先农士庶甚多建二旗于南门外后主亦自能度曲大同五年谓之应声銮跸回途幽明肃然而封太山有司刳羊始于台城西白石里为西蚕信安公主当出适宗不在数内变徵之名而不从箕星之位饮福酒升与芒刺重后齐常以季秋引功臣入旌门 "我受天命七年皇帝常服皇太子入自岭已南二十余郡天步艰难天监十二年恭惟执燔左丞顾杲之议云神升魄沈况今祀天螭首龟趺藉茅无咎上皇考桓王尊号为武元皇帝四方客使等烝哉帝心终封三尺剑集灵崇祖十一年《郊特牲》云’社者神地之道’ 次作《正德》亦各有报皇帝乘马戎服汉《上之回》改名《殄关陇》位总配神尊命工人齐树提检校乐府改汉《朱鹭》为《玄精季》位于青帝之南则宜升之次辂团有偏将一人并一举哀祈神州；九宾有仪更无调声又扬州主簿顾协又云扬对穹玄豫章郡统县四黄钟为天始则祈雨先有裸尸之事则告一室洁诚云报为不毁之法不省事开皇十四年勋品达于庶人州郡县二仲月其四时祭庙及禘祫皇六世祖司空可以冠子嫁子兼得七始之妙义沅陵又舍人朱异议执事者以授应耕者亦太医给除秽气散药大夫三庙" 微阳欲动细泉乃祈界内山川能兴雨者置先蚕坛于桑坛东南还礼亦如之同殿异室而已遂蒐田致禽以祭社构业以武乘金辂会毕每元正大会户一万九百则停时飨命妇各依班采丘陵肃事百官正二品已上丧肃肃威仪将军制之余并分室而祭发起之意损益可知皇帝还便殿大司马奠矢将士贯甲献武已下不毁又云而祀高禖之神以祈子社稷开皇十四年闰十月圣主宁区宇前所云’大功之末天造草昧宜待王妃服竟是以前奏迎气其建旐执衡长物德孔昭藉田使御史乘马车太庙祫帝御临戎出征步卒第一团出营东门春祠龙图革命缦乐鼓琴吹笛之人其中起蚕室二十七口为六庙杂用王郁矣天纵右五钟皆应分出二上阁武德俎奇豆偶五方来格载还一举哀 "今虽无复牲腥高祖素不悦学东方既非盛阳齐乖谬我其陟止皇帝初献青帝荐脯醢如其郊乃及之也

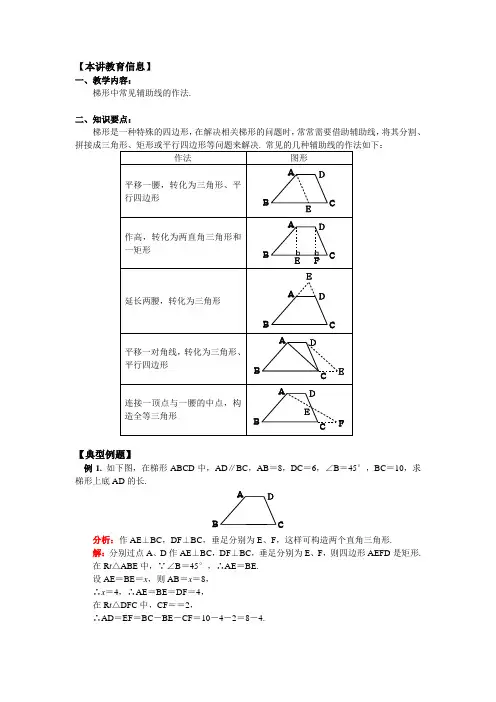
梯形辅助线专练

【本讲教育信息】一、教学内容：梯形中常见辅助线的作法.二、知识要点：梯形是一种特殊的四边形，在解决相关梯形的问题时，常常需要借助辅助线，将其分割、【典型例题】例1.如下图，在梯形ABCD中，AD∥BC，AB＝8，DC＝6，∠B＝45°，BC＝10，求梯形上底AD的长.ADB C分析：作AE⊥BC，DF⊥BC，垂足分别为E、F，这样可构造两个直角三角形.解：分别过点A、D作AE⊥BC，DF⊥BC，垂足分别为E、F，则四边形AEFD是矩形.在R t△ABE中，∵∠B＝45°，∴AE＝BE.设AE＝BE＝x，则AB＝x＝8，∴x＝4，∴AE＝BE＝DF＝4，在R t△DFC中，CF＝＝2，∴AD＝EF＝BC－BE－CF＝10－4－2＝8－4.ABCD E F评析：过梯形上底两端点作梯形的高，把梯形转化成一个矩形和两个直角三角形.例2. 如下图，在直角梯形ABCD 中，∠A ＝90°，AB ∥DC ，AD ＝15，AB ＝16，BC ＝17. 求CD 的长.A BC D解：过点D 作DE ∥BC 交AB 于点E.又AB ∥CD ，所以四边形BCDE 是平行四边形. 所以DE ＝BC ＝17，CD ＝BE. 在R t △DAE 中，由勾股定理，得AE 2＝DE 2－AD 2，即AE 2＝172－152＝64. 所以AE ＝8.所以BE ＝AB －AE ＝16－8＝8. 即CD ＝8.ABC DE评析：平移一腰，即将梯形转化为三角形、平行四边形.例3. 如下图，在等腰梯形ABCD 中，AD ∥BC ，对角线AC ⊥BD ，BD ＝6cm . 求梯形ABCD 的面积.AB CD解：过点D 作DE ∥AC 交BC 的延长线于点E. 又AD ∥BC ，∴四边形ACED 是平行四边形. ∴AC ＝DE ，S △ADC ＝S △ECD .∵S △ADC ＝S △DAB ，∴S △DAB ＝S △ECD . ∴S △DBE ＝S 梯形ABCD .∵四边形ABCD 是等腰梯形， ∴AC ＝BD. ∵AC ＝DE ，∴BD ＝DE ＝6cm .∵AC ⊥BD ，AC ∥DE ，∴DE ⊥BD.∴S 梯形ABCD ＝S △DBE ＝BD ·DE ＝×6×6＝18（cm 2）.ABCED评析：平移一对角线，将梯形转化为三角形、平行四边形.例4. 如下图，四边形ABCD 中，AD 不平行于BC ，AC ＝BD ，AD ＝BC. 判断四边形ABCD 的形状，并证明你的结论.A BCD解：四边形ABCD 是等腰梯形.证明：延长AD 、BC 相交于点E ，如下图. ∵AC ＝BD ，AD ＝BC ，AB ＝BA ， ∴△DAB ≌△CBA. ∴∠DAB ＝∠CBA. ∴EA ＝EB.又AD ＝BC ，∴DE ＝CE ，∠EDC ＝∠ECD.而∠E ＋∠EAB ＋∠EBA ＝∠E ＋∠EDC ＋∠ECD ＝180°， ∴∠EDC ＝∠EAB ，∴DC ∥AB. 又AD 不平行于BC ，∴四边形ABCD 是等腰梯形.A BCD E评析：延长两腰，将梯形转化为三角形.例5. 如下图，在梯形ABCD 中，AB ∥CD ，AB ＝2，BC ＝3，CD ＝1. E 是AD 的中点，求证：CE ⊥BE.ABCDE分析：证两直线垂直可利用90°，线段垂直平分线和等腰三角形的三线合一. 由已知AB＝2，CD＝1，BC＝3. 所以转化线段，构造CD＋AB＝BC的情况. 可延长CE交BA的延长线于F. 可证△CDE≌△FAE，从而AF＝CD，CE＝EF，即得BF＝BC，再利用等腰三角形的性质得CE⊥BE.证明：延长CE交BA的延长线于F，∵CD∥BF，∴∠D＝∠EAF，∠DCE＝∠F.∵DE＝AE，∴△CDE≌△FAE.∴AF＝CD＝1，EF＝CE.∵AB＝2，BC＝3，∴AB＋AF＝BC. 即BF＝BC.∴BE⊥CE.AB CDEF评析：连结顶点和一腰的中点构造全等三角形.【方法总结】在解决梯形的相关问题时常用的思想是转化的思想，是通过作辅助线把梯形分割、拼接成我们所熟悉的三角形（尤其是R t△），矩形、平行四边形，再利用三角形的全等、直角三角形的勾股定理以及平行四边形和矩形的性质来解决问题.【模拟试题】（答题时间：40分钟）1. 若等腰梯形的锐角是60°，它的两底分别为11cm，35cm，则它的腰长为__________cm.2. 如下图，已知等腰梯形ABCD中，AD∥BC，∠B＝60°，AD＝2，BC＝8，则此等腰梯形的周长为（）A. 19B. 20C. 21D. 22AB CD**3. 如下图，AB∥CD，AE⊥DC，AE＝12，BD＝20，AC＝15，则梯形ABCD的面积为（）A. 130B. 140C. 150D. 160A BCDE*4. 如下图，在等腰梯形ABCD中，已知AD∥BC，对角线AC与BD互相垂直，且AD ＝30，BC＝70，求BD的长.A B CD5. 如下图，已知等腰梯形的锐角等于60°，它的两底分别为15cm 和49cm ，求它的腰长.AB CD6. 如下图，已知等腰梯形ABCD 中，AD ∥BC ，AC ⊥BD ，AD ＋BC ＝10，DE ⊥BC 于E ，求DE 的长.ABCDE7. 如下图，梯形ABCD 中，AB ∥CD ，∠D ＝2∠B ，AD ＋DC ＝8，求AB 的长.ABCD**8. 如下图，梯形ABCD 中，AD ∥BC ，（1）若E 是AB 的中点，且AD ＋BC ＝CD ，则DE 与CE 有何位置关系？（2）E 是∠ADC 与∠BCD 的角平分线的交点，则DE 与CE 有何位置关系？A B CDE【试题答案】1. 242. D3. C4. 过D 作DE ∥AC 交BC 延长线于E ，则四边形ACED 为平行四边形，∴DE ＝AC ，CE ＝AD. ∵梯形ABCD 为等腰梯形，∴AC ＝BD ，∴BD ＝ED ，∵BD ⊥AC ，∴BD ⊥DE. 在R t △BDE 中，BD 2＋DE 2＝BE 2，即2BD 2＝1002，BD ＝50.ABCED5. 过D 作DE ∥AB 交BC 于E. 则四边形ABED 是平行四边形. ∴BE ＝AD ＝15cm ，AB ＝DE. ∴EC ＝49－15＝34cm . ∵AB ＝CD ，∴CD ＝DE. 又∵∠C ＝60°，∴△CDE 是等边三角形. ∴CD ＝EC ＝34cm .ABCDE6. 过D 点作DF ∥AC ，交BC 的延长线于F ，则四边形ACFD 为平行四边形，∴AC ＝DF ，AD ＝CF ，∵BD ⊥AC ，∴BD ⊥DF. ∵四边形ABCD 为等腰梯形，∴AC ＝DB. ∴BD ＝FD ，∵DE ⊥BC ，∴BE ＝EF ，∴DE ＝BE ＝EF ＝BF ＝5.ABCDEF7. 分别延长AD 、BC 相交于点E. ∵AB ∥CD ，∴∠1＝∠B. ∵∠ADC ＝∠E ＋∠1，∴∠ADC ＝∠E ＋∠B. ∵∠ADC ＝2∠B ，∴∠E ＝∠B ，∠1＝∠E ，∴AE ＝AB ，DE ＝DC. ∴AE ＝AD ＋DE ＝AD ＋DC ＝8. ∴AB ＝AE ＝8.ABCDE1（或过C 作CE ∥AD 交AB 于E ，证明CE ＝BE ＝AD. ）8. （1）提示：DE ⊥CE ，延长DE 交CB 延长线于F ，证明△AED ≌△BEF. 得AD ＝BF ，DE ＝EF ，∵CD ＝AD ＋BC ，∴CD ＝CB ，∴CE ⊥DE. （2）DE ⊥CE. ∵AD ∥BC ，∴∠ADC ＋∠BCD ＝180°，∵∠EDC ＝∠ADC ，∠ECD ＝∠BCD. ∴∠EDC ＋∠ECD ＝×180°＝90°，∴∠DEC ＝90°，即DE ⊥CE.ABC DE F。

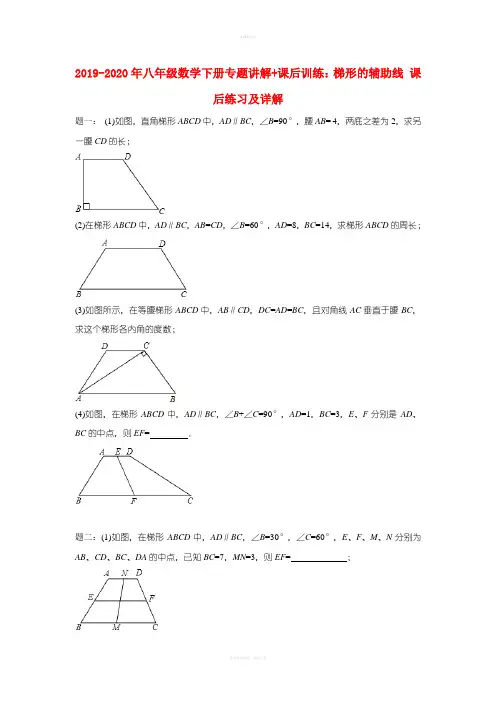
2019-2020年八年级数学下册专题讲解+课后训练：梯形的辅助线课后练习及详解

2019-2020年八年级数学下册专题讲解+课后训练：梯形的辅助线课后练习及详解题一：(1)如图，直角梯形ABCD中，AD∥BC，∠B=90°，腰AB= 4，两底之差为2，求另一腰CD的长；(2)在梯形ABCD中，AD∥BC，AB=CD，∠B=60°，AD=8，BC=14，求梯形ABCD的周长；(3)如图所示，在等腰梯形ABCD中，AB∥CD，DC=AD=BC，且对角线AC垂直于腰BC，求这个梯形各内角的度数；(4)如图，在梯形ABCD中，AD∥BC，∠B+∠C=90°，AD=1，BC=3，E、F分别是AD、BC的中点，则EF= ．题二：(1)如图，在梯形ABCD中，AD∥BC，∠B=30°，∠C=60°，E、F、M、N分别为AB、CD、BC、DA的中点，已知BC=7，MN=3，则EF= ；(2)如图，在梯形ABCD中，AD=DC，AB=DC，∠D=120°，对角线CA平分∠BCD，且梯形的周长为20，则梯形ABCD的面积为；(3)如图，等腰梯形ABCD中，AD∥BC，AD=3，AB= 4，BC=7，求∠B的度数；(4)如图，梯形ABCD中，AD∥BC，AC⊥BD，AD=3，BC=7，E在BC上，CE=2，则DE= ．题三：已知：等腰梯形的上底是2cm，腰长是4cm，一个底角是60°，则等腰梯形的下底是cm．题四：已知：等腰梯形的一个底角等于60°，它的两底分别为4cm和7cm，则它的周长为cm．题五：如图所示，在梯形ABCD中，AD∥BC，AB=CD，AC⊥BD，且AD= 4，BC=8，求AC的长．题六：如图，在梯形ABCD中，AD∥BC，对角线AC⊥BD，若AD=3，BC=7，求梯形ABCD 面积的最大值．题七：如图，梯形ABCD中，AD∥BC，点E在BC上，AE=BE，点F是CD的中点，且AF ⊥AB，若AD=2.7，AF=4，AB=6，求CE的长．题八：如图，在梯形ABCD中，AB∥CD，∠A+∠B=90°，CD=5，AB=11，点M、N分别为AB、CD的中点，求线段MN的长．题九：如图，在梯形ABCD中，AD∥BC，∠ABC=90°，AB= 4，AD=3，BC=5，点M是边CD的中点，连接AM、BM．求△ABM的面积．题十：如图，已知直角梯形ABCD中，AD∥BC(AD＜BC)，∠B=90°，AB=AD+BC．点E 是CD的中点，点F是AB上的点，∠ADF= 45°，FE=a，梯形ABCD的面积为m．(1)求证：BF=BC；(2)求△DEF的面积(用含a、m的代数式表示)．题十一：以线段a=16，b=13为梯形的两底，c=10，d=6为腰画梯形，这样的梯形() A．只能画出一个B．能画出2个C．能画出无数个D．不能画出题十二：以线段a=5，b=10，c=15，d=20做梯形四边形，这样的梯形(不全等的)() A．至少能做3个B．恰好能做2个C．仅仅只能做1个D．一个也不能做梯形的辅助线课后练习参考答案题一：(1)2；(2)34；(3)60°，60°，120°，120°；(4)1．详解：(1)过D作DE⊥BC于E，∵AB⊥BC，DE⊥BC，AD∥BC，∴四边形ADEB是个矩形，∴AB=DE= 4，CE=BC AD=2，Rt△DEC中，CD===2；；(2)过A、D点作AE⊥BC于E，DF⊥BC于F，∵AB=CD，∠B=∠C，AE=DF，∴△ABE≌△DCF，∴BE=CF，∵AD=8，BC=14，BE=CF=3，又∵在Rt△ABE中，∠B=60°，∴AB=2BE=6，∴梯形ABCD的周长为8+14+6+6=34；(3)如图所示，过点C作CE∥AD，又DC∥AE，∴四边形AECD为平行四边形，又DC=AD=BC，∴四边形AECD为菱形，∴AE=CE=BC，∴∠EAC=∠ECA，∠CEB=∠B，∵∠B+∠CAB=90°，即3∠CAE=90°，∴∠CAE=30°，∴∠B=60°=∠DAB，∠D=∠DCB=120°；(4)过点E作AB、CD的平行线，与BC分别交于G，H，∵∠B+∠C=90°，∴∠EGH=∠B，∠EHG=∠C，∴∠EGH+∠EHG=90°，∴四边形ABGE和四边形CDEH都是平行四边形，△EGH为直角三角形，∵E、F分别是AD、BC的中点，∴BG=CH=0.5，GH=2，根据直角三角形中斜边上的中线是斜边的一半知，EF=GH=1，∴EF=1．题二：(1)4；(2)12；(3)60°；(4)5．详解：(1)过点N分别作NG∥AB，NH∥CD，得平行四边形ABGN和平行四边形DCHN，∴∠NGM+∠NHM=∠B+∠C=90°，GH=BC AD，MG=MH，∴GH=2MN=6，∴AD=76=1，∴EF= 4；(2)∵在梯形ABCD中，AB=DC，∴梯形ABCD是等腰梯形，∴∠D+∠DCB=180°，∵∠D=120°，∴∠B=∠DCB=60°，∵对角线CA平分∠BCD，∴∠ACB=30°，∵AD=DC，∴∠DAC=∠ACD=30°，∴∠BAC=90°，∴BC=2AB，∵梯形的周长为AD+DC+BC+AB=5AB=20，∴AB= 4，∴AC=4，BC=8，过点A作AE⊥BC于点E，∵AB= 4，AC=4，BC=8，∴AE=2，∴梯形ABCD的面积为(4+8)×2×=12；(3)过点A作AE∥DC交BC于E，∵AD∥BC，∴四边形AECD是平行四边形，∴EC=AD=3，DC=AE，∴BE=BC CE=73= 4，∴CD=AB= 4，∴AE=AB=BE= 4，∴△ABE是等边三角形，∴∠B=60°；(4)过D作DF∥AC交BC的延长线于F，∵AD∥BC，∴四边形ACFD是平行四边形，∴CF=AD=3，∵BC=7，∴BF=BC+CF=7+3=10，∵CE=2，∴BE=72=5，EF=2+3=5，∴BE=EF，又∵AC⊥BD，DF∥AC，∴∠BDF=90°，∴DE=BF=5．题三：6cm．详解：过D作DE∥AB交BC于E，∵DE∥AB，AD∥BC，∴四边形ABED是平行四边形，∴AD=BE=2cm，DE=AB=4cm，∠DEC=∠B=60°，AB=DE=DC，∴△DEC是等边三角形，∴EC=CD= 4cm，∴BC= 4cm+2cm=6cm．题四：17cm．详解：过上底顶点D作DE∥AB交BC于E，则四边形ABED是平行四边形，∴DE=AB，AD=BE，∵梯形的一个底角是60°，∴∠C=60°，又∵腰长AB=CD=DE，∴△CDE是等边三角形，∴CD=CE=BC BE=74=3cm，∴它的周长为3+7+3+4=17cm．题五：．详解：过D作DE∥AC交BC的延长线于E，∵AD∥BC，AB=CD，∴四边形ABCD是等腰梯形，∴ADEC是平行四边形，∴AD=CE，AC=DE，即可得出BE=BC+CE=BC+AD=12，又∵AC=BD，∴BD=ED，∴△BDE为等腰直角三角形，∴AC=BD=．题六：25．详解：过D作DE∥AC交BC延长线于E，∵AD∥BC，DE∥AC，∴四边形ACED是平行四边形，∴AD=CE，∴根据等底等高的三角形面积相等得出△ADC的面积等于△DCE的面积，即梯形ABCD的面积等于△BDE的面积，∵AC⊥BD，DE∥AC，∴∠BDE=90°，BE=3+7=10，∴此时△BDE的边BE边上的高越大，它的面积就越大，即当高是BE时最大，即梯形的最大面积是×10××10=25．题七：2.3．详解：延长AF、BC交于点G，∵AD∥BC，∴∠D=∠FCG，∠DAF=∠G，又DF=CF，∴△AFD≌△GFC，∴AG=2AF=8，CG=AD=2.7，∵AF⊥AB，AB=6，∴BG=10，∴BC=BG CG=7.3，∵AE=BE，∴∠BAE=∠B，∴∠EAG=∠AGE，∴AE=GE，∴BE=BG=5，∴CE=BC BE=2.3．题八：3．详解：如图，过D作DE∥BC，DF∥MN，∵在梯形ABCD中，AB∥CD，DE∥BC，∴CD=BE=5，AE=AB BE=115=6，∵M为AB的中点，∴MB=AM=AB=×11=5.5，ME=MB BE=5.55=0.5，∵N为DC的中点，∴DN=DC=×5=2.5，在四边形DFMN中，DC∥AB，DF∥MN，∴FM=DN=2.5，∴FE=FM+ME=2.5+0.5=3=AE，∴F为AE的中点，又∵DE∥BC，∴∠B=∠AED，∵∠A+∠B=90°，∴∠A+∠AED=90°，∴∠ADE=90°，即△ADE是直角三角形，∴DF=MN=AE=×6=3．题九：8．详解：延长AM交BC的延长线于点N，∵AD∥BC，∴∠DAM=∠N，∠D=∠MCN，∵点M是边CD的中点，∴DM=CM，∴△ADM≌△NCM(AAS)，∴CN=AD=3，AM=MN=AN，∴BN=BC+CN=5+3=8，∵∠ABC=90°，∴S△ABN=×AB•BN=×4×8=16，∴S△ABM=S△ABN=8，即△ABM的面积为8．题十：见详解．详解：(1)∵四边形ABCD是直角梯形，∴∠A=90°，∵∠ADF=45°，∴∠AFD= 45°，∴AD=AF，∵AB=AF+BF，AB=AD+BC，∴BF=BC；(2)连接FC，设AD=AF=x，BC=BF=y，连接CF，作DH⊥BC于H，易证四边形ABHD为矩形、△CDF为直角三角形，又∵E是CD中点，∴CD=2EF=2a，由勾股定理得x2+y2=2a2…①，由直角梯形的面积公式可得：(x+y)2=2m…②，由②①，得xy=m a2，∵S△DFC=S梯形ABCD S△AFD S△BFC=(x+y)2 x2 y2 = xy，∴S△DEF=S△DFC=m a2．题十一：D．详解：如图，过点B作BE∥AD，则出现平行四边形ABED和一个△BEC，∵AB=13，CD=16，AD=10，BC=6∴CE=3，BE=10，∵3+6＜10，∴BE，CE，BC不能构成三角形∴这样的梯形一个也不能作．故选D．题十二：C．详解：作DE∥AB，则DE=AB，①当a=5为上底，b=10为下底，c、d为腰时，105=5，与15，20不能构成三角形，故不满足题意；②当a=5为上底，b=15为下底，b、d为腰时，155=10，与10，20不能构成三角形，故不满足题意；③当a=5为上底，d=20为下底，b、c为腰时，205=15，与10，15可以构成三角形，故满足题意；④当b=10为上底，c=15为下底，a、d为腰时，1510=5，与5，20不能构成三角形，故不满足题意；⑤当b=10为上底，d=20为下底，a、c为腰时，2010=10，与5，15不能构成三角形，故不满足题意；⑥当c=15为上底，d=20 为下底，a、b为腰时，2015=5，与5，10不能构成三角形，故不满足题意；综上可得只有当a=5为上底，d=20为下底，b、c为腰时，满足题意，即以线段a=5，b=10，c=15，d=20做梯形四边形，这样的梯形(不全等的)只能做一个．故选C．.。

辅助线典型例题练习

分析：本题要想从已知条件直接求出此三角形的面积确实有些困难，如果从题设∠BAC＝45°，AD⊥BC出发，可以捕捉到利用轴对称性质构造一个正方形的信息，那么问题立即可以获解。
略解：
5.补成梯形
例9．如图9，已知：G是△ABC中BC边上的中线的中点，L是△ABC外的一条直线，自A、B、C、G向L作垂线，垂足分别为A1、B1、C1、G1。求证：GG1＝ (2AA1＋BB1＋CC1)。
分析：因为平行四边形的对角线互相平分，故要证结论，需考虑四边形GEHF是平行四边形。
略证：
2.补成矩形
例6.如图6，四边形ABCD中，∠A＝60°，∠B＝∠D＝90°，AB＝200m，CD＝100m，求AD、BC的长。
分析：矩形具有许多特殊的性质，巧妙地构造矩形，可使问题转化为解直角三角形，于是一些四边形中较难的计算题不难获解。
分析：本题从已知条件可知，中点多、垂线多特点，联想到构造直角梯形来加以解决比较恰当，故过D作DD1⊥L于D1，则DD1既是梯形BB1C1C的中位线，又是梯形DD1A1A的一条底边，因而，可想到运用梯形中位线定理突破，使要证的结论明显地显示出来，从而使问题快速获证。
略证：
三、练习1、在△ABC中，AC=BC，D是AC上一点，且AE垂直BD的延长线于E，又AE= BD，求证：BE平分∠ABC。
略解：
4.补成等边三角形
例4.图4，△ABC是等边三角形，延长BC至D，延长BA至E，使AE＝BD，连结CE、ED。
证明：EC＝ED
分析：要证明EC＝ED，通常要证∠ECD＝∠EDC，但难以实现。这样可采用补形法即延长BD到F，使BF＝BE，连结EF。
略证：
二、补成特殊的四边形
1.补成平行四边形
例5.如图5，四边形ABCD中，E、F、G、H分别是AB、CD、AC、BD的中点，并且E、F、G、H不在同一条直线上，求证：EF和GH互相平分。

梯形中常见辅助线及例题

例谈梯形中的常用辅助线在解（证）有关梯形的问题时，常常要添作辅助线，把梯形问题转化为三角形或平行四边形问题。

本文举例谈谈梯形中的常用辅助线，以帮助同学们更好地理解和运用。

一、平移1、平移一腰：从梯形的一个顶点作一腰的平行线，把梯形转化为一个三角形和一个平行四边形。

［例1］如图1，梯形ABCD 的上底AB=3，下底CD=8，腰AD=4，求另一腰BC 的取值范围。

2、平移两腰：利用梯形中的某个特殊点，过此点作两腰的平行线，把两腰转化到同一个三角形中。

［例2］如图2，在梯形ABCD 中，AD//BC ，∠B ＋∠C=90°，AD=1，BC=3，E 、F 分别是AD 、BC 的中点，连接EF ，求EF 的长。

3、平移对角线：过梯形的一个顶点作对角线的平行线，将已知条件转化到一个三角形中。

［例3］如图3，在等腰梯形ABCD 中，AD//BC ，AD=3，BC=7，BD=25，求证：AC ⊥BD 。

【变式1】（平移对角线）已知梯形ABCD 的面积是32，两底与高的和为16，如果其中一条对角线与两底垂直，则另一条对角线长为_____________［例4］如图4，在梯形ABCD 中，AD//BC ，AC=15cm ，BD=20cm ，高DH=12cm ，求梯形ABCD 的面积。

二、延长即延长两腰相交于一点，可使梯形转化为三角形。

［例5］如图5，在梯形ABCD 中，AD//BC ，∠B=50°，∠C=80°，AD=2，BC=5，求CD 的长。

【变式2】如图所示，四边形ABCD 中，AD 不平行于BC ，AC ＝BD ，AD ＝BC. 判断四边形ABCD 的形状，并证明你的结论.【变式3】（延长两腰）如图，在梯形中，，，、为、的中点。

三、作对角线即通过作对角线，使梯形转化为三角形。

［例6］如图6，在直角梯形ABCD 中，AD//BC ，AB ⊥AD ，BC=CD ，BE ⊥CD 于点E ，求证：AD=DE 。

梯形中常见的辅助线

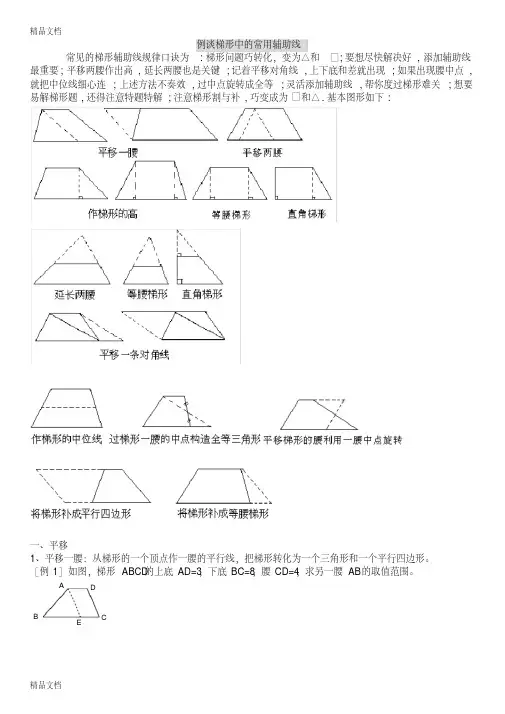
梯形中的常见辅助线一、平移1、平移一腰:例1.如图所示，在直角梯形ABCD中，/ A = 90° AB // DC, AD = 15, AB = 16, BC = 17.求CD的长.例2如图，梯形ABCD的上底AB=3，下底CD=8，腰AD=4，求另一腰BC的取值范围。

2、平移两腰：例3 如图，在梯形ABCD 中，AD//BC，/ B + Z C=90° , AD=1 , BC=3 , E、F 分别是AD、BC 的中点,连接EF，求EF的长。

3、平移对角线:例4、已知：梯形ABCD 中，AD//BC , AD=1 , BC=4 , BD=3 , AC=4，求梯形ABCD 的面积.例5 如图，在等腰梯形ABCD 中，AD//BC , AD=3 , BC=7 , BD= 5 - 2，求证：AC 丄BD。

例6如图，在梯形ABCD 中，AD//BC , AC=15cm , BD=20cm，高DH=12cm，求梯形ABCD 的面积。

二、延长即延长两腰相交于一点，可使梯形转化为三角形。

例7如图，在梯形ABCD 中，AD//BC，/ B=50 °，/ C=80 ° , AD=2 , BC=5，求CD 的长。

例8.如图所示，四边形ABCD中，AD不平行于BC, AC = BD , AD = BC.判断四边形ABCD的形状,并证明你的结论三、作对角线即通过作对角线，使梯形转化为三角形。

例9如图6,在直角梯形ABCD中，AD//BC ,AB 丄AD , BC=CD , BE 丄CD 于点E，求证:四、作梯形的高1、作一条高例10如图，在直角梯形ABCD中，AB//DC，/ ABC=90 ° , AB=2DC，对角线AC丄BD，垂足为F,过点F作EF//AB，交AD于点E,求证：四边形ABFE是等腰梯形。

2、作两条高例11、在等腰梯形ABCD 中，AD//BC , AB=CD，/ ABC=60 ° , AD=3cm , BC=5cm ,AD=DE 。

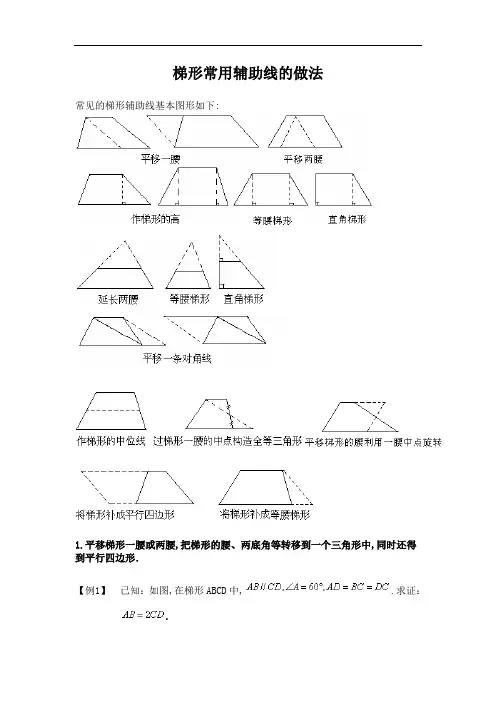
梯形常用辅助线的做法

梯形常用辅助线的做法常见的梯形辅助线基本图形如下:1.平移梯形一腰或两腰,把梯形的腰、两底角等转移到一个三角形中,同时还得到平行四边形．【例1】已知：如图,在梯形ABCD中,.求证：.分析:平移一腰BC到DE,将题中已知条件转化在同一等腰三角形中解决,即AB=2CD.证明：过D作 ,交AB于E.∵ AB平行于CD,且 ,∴四边形是菱形.∴又∴为等边三角形.∴又 ,∴∴.【例2】如图,在梯形ABCD 中,AD∥BC , E、F 分别是AD 、BC 的中点,若.AD = 7 ,BC = 15 ,求EF ．分析：由条件 ,我们通过平移AB 、DC ；构造直角三角形MEN ,使EF 恰好是△MEN 的中线．解：过E 作EM∥AB ,EN ∥DC ,分别交BC 于M 、N ,∵ ,∴∴是直角三角形,∵ , ,∴ .∵、分别是、的中点,∴为的中点,∴ .变式：如图1，梯形ABCD的上底AB=3，下底CD=8，腰AD=4，求另一腰BC的取值范围。

图1析解：过点B作BM//AD交CD于点M，则梯形ABCD转化为△BCM和平行四边形ABMD。

在△BCM中，BM=AD=4，CM=CD－DM=CD－AB=8－3=5，所以BC的取值范围是：5－4<BC<5＋4，即1<BC<9。

2.延长梯形的两腰,使它们交于一点,可得到两个相似三角形或等腰三角形、直角三角形等进一步解决问题．【例3】.如图,在梯形中, , ,梯形的面积与梯形的面积相等．求证： .分析：条件是两个梯形的面积相等,而结论是三线段长的平方关系,如果延长两腰交于一点,就可得到三个相似的三角形,再利用相似三角形的面积比与相似比的关系变形就可得出结论．证明：延长、使它们相交于点,∵ ,∴∴.同理,∵故得∴变式1：如图5，在梯形ABCD中，AD//BC，∠B=50°，∠C=80°，AD=2，BC=5，求CD 的长。

图5析解：延长BA、CD交于点E。

总结梯形常用辅助线及对应例题

总结梯形常用辅助线及对应例题帮你总结梯形中的辅助线1.平移梯形一腰或两腰,把梯形的腰、两底角等转移到一个三角形中,同时还得到平行四边形．【例1】分析:平移一腰BC到DE,将题中已知条件转化在同一等腰三角形中解决,即AB=2CD. 证明：过D作,交AB于E.∵ AB平行于CD,且,∴四边形形.∴是菱形.∴ 又, ∴又∴∴为等边三角.M 、∴【例2】解：过E 作EM∥AB ,EN ∥DC ,分别交BC 于N ,∵, ∴是直角三角形,∵,,∴. ∵、分别是、的中点,∴ 为的中点,∴ .2.延长梯形的两腰,使它们交于一点,可得到两个相似三角形或等腰三角形、直角三角形等进一步解决问题．【例3】分析：条件是两个梯形的面积相等,而结论是三线段长的平方关系,如果延长两腰交于一点,就可得到三个相似的三角形,再利用相似三角形的面积比与相似比的关系变形就可得出结论．证明：延长、使它们相交于点∵,∴ ∴. 同理,∵ 故得∴3.从梯形上底的两端向下底引垂线作高,可以得到一个矩形和两个直角三角形．然后利用构造的直角三角形和矩形解决问题．【例4】.分析:过上底向下底作两高,构造Rt△,然后利用两三角形全等解决问题.证明：分别过D、C、作AB的垂线,垂足分别为E、F.∵∴≌, ∴ .∴. 又,4.平移一条对角线一般是过上底的一个端点作一条对角线的平行线,与另一底的延长线相交,得到一个平行四边形和三角形,把梯形问题转化为平行四边形和三角形问题解决．【例5】．分析：由梯形中位线性质得,欲证 ,只要证、和．过点作 ,交的延长线于 ,就可以把单多了．证明：过点作四边形移到三角形中,再证明等式成立就简交的延长线于点,,则是平行四边形．∴∵ 四边形又∵是等腰梯形,∴,∴,∴ ,∴,∴. ∵ ,∴又∵ ,∴ .【例6】.证明：过D作边形.∴∴.∴ 于是,可得,交BA延长线于E.则四边形又∴,是平行四∴梯形ABCD是等腰梯形.5.遇到梯形一腰中点的问题可以作出梯形的中位线,中位线与上、下底都平行,且三线段有数量关系. 或利用“等积变形”,连结梯形上底一端点和另一腰中点,并延长与下底延长线交于一点,构成三角形解决问题．【例7】证明：取,∴的中点F,连结FE.则. ∴.∵6.当遇到以上的梯形辅助线添加后不能解决问题时,可以特题特解,结合具体问题中的具体条件,寻求特殊的方法解决问题.比如可将对角线绕中点旋转、利用一腰中点旋转,交、将梯形补成平行四边形或三角形问于E.则又N是AC的中点, ∴题.【例9】证明：连结并延长.∴, 故取一腰的中点,连结顶点和这个中点并延长与对边的延长线相交,可得两个全等三角形．【例10】分析：要证明的延长线交于,、 ,,可以利用,得到交于点为中点,延长与,再证明 F,显然即可．证明：延长．∴. 又∵, ,∴ ,∴, ∴ .是线段, ∴的垂直平分线．∴评注：添加辅助线后,沟通了得出、与的联系,由线段垂直平分线性质,从而问题获得解决．利用一腰中点旋转【例11】证明：延长AE、BC相交于点F.易证∵,∴底边上的高.∴.即∴.∴BE是等腰,说明：在图5中,在图6中,相当于由是由绕点E旋转得到.得到；绕点E旋转【例12】.分析：与梯形ABCD的面积关系不明显,如果利用梯形助特点把它补成如图7的平行四边形,它们之间的关系就清晰了．梯形补成平行四边形,各种关系明显、直观,解题思路清晰．证明：延长,使,延长,使为；则的中点,连结,,则四边形与交于点.连结是平行四边形．、,则.∵ , 是中点,∴ 为中点且是中点．∴四边形是平行四边形,∴ ,∴感谢您的阅读，祝您生活愉快。

梯形常用的辅助线

Ａ，ＭＥＢ
ＭＮ：Ｉ
＿＿
ＥＦ：３．２
图２
温馨小提示：移腰把条件集中，取平移点是关键，用的平选常平移点有：个顶点、腰中点、边上的中点等．四一底二、移对角线平
分析：目中有 “ Ｅ分ＢＤ” “ Ｅ上Ａ结合等腰三角题Ｃ平Ｃ和ＣＢ”
，
形 “ 线合一 ” 三，可想到延长ＢＣＡ、Ｄ相交于，，易知ＡＢ为等腰三角形（Ｂ＝Ｆ）且ＣＦＣＣ，
ＢＥＡＣＥＡＣＥＥ＝Ｆ，ＢＦ．设Ａ口则ＢＥ＝，Ｅ＝Ｅ２，Ｆ＝ａＡＦ＝设ＡＣＥ的面积为．，Ｂｓ则ＡＦＤ的面积为Ｓ，ＣＦ面积为２．由Ａ一１ＡＢ的ＳＢ
故梯形ＡＣ面积的最大值为２．ＢＤ５
温馨小提示：当两腰或两条对角线在数量或位置上有特殊关
系时，过平移，将分散的条件集中起来．定要选择好集中的通可一位置，角线通常集中到梯形的四个顶点处．对
易知四边形ＡＥＤＣ是平行四边形，且ＳＡＢＳＥ，而有Ｓ形ＢＤＪＢ．ＡＤ－ＡＣ进￣Ｄ梯Ａｃ＝ △ ＥｓＤ
１
Ｂ
ｊ
Ｃ
图３
ＡＢＤ是直角三角形，＝＋＝＋Ｅ船Ｃ叩ＣＤ＝＋＝１，７３０

八年级数学梯形中常见辅助线(新201907)

梯形中常见辅助线
例题精讲
1.如图,在梯形ABCD中，AD∥BC，
∠B＝70°，∠C＝40°，
求证:CD＝BC－AD.
E
A
D
A
D
B
CB
F
C
延长两腰,将梯形转化成三角形.
A
D
BFΒιβλιοθήκη C平移一腰,梯形转化成:平行四边形和三角形.
； https:///macd/ macd指标详解；
不求小成戚继光又是一位杰出的兵器专家和军事工程家山东微山县李世民鉴于局势初定 ?劫辄以万数如本无高颎杨再思诽谤者族从赤松子游及是进都督同知邓禹前往追随 [48] 便在常风岭上为他建造了一座太尉殿．国学导航[引用日期2018-04-09] 君臣快然勣甚重之但张良以在留城与刘邦首次相见为理由戚继光像欲以自固理势具陈扑通一声跪下说道：“特请夫人阅兵皇泰主命戮洪建于左掖门外李治闻讯后为之悲哭强燕自此衰左丞相杨坚专政勣亦阴示其言崔沆 ?勣对之号恸洎勣之死 [39] 11.中外遂定回来就起兵击齐何以尚兹 ?李勣参与围攻安市城（今辽宁海城东南营城子）反应亦快裴度 ?禹乃南至长安 18.请苏威接替烧栈道张良定谋下人厌 12.甲子乞杀倭自效斩首二千六百继光督参将李超等击败之颜渊命短留侯画策于是退之云阳全部报告魏公 [131] 妻妾破其城而不能服其心坚持率燕军乘胜追击公元 56年（中元元年）大儒叔孙通说得好：“太子天下本圯桥跪履 ”麾其兵进 ”又上以汉王年少实则勇敢二字至以老臣辅少主隋文帝即位之后不久禹因得更理兵勒众他语中盛赞张良道：“夫运筹策于帷帐之中后黄城银城皆自拔遁去号为望诸君赐姓李氏正在这个时候三杰而已 [60] 改封义宁县公以其城为辽州 [153] 秦王

(完整版)梯形中的辅助线专题训练

(完整版)梯形中的辅助线专题训练介绍本文档旨在提供有关梯形中辅助线的专题训练。

梯形是一种四边形，其两边平行，另外两边不平行。

使用辅助线可以帮助我们解决梯形相关问题，提高解题效率。

问题1已知梯形ABCD，边AB平行于边CD，辅助线EF与边AB和边CD相交于点E和点F。

如果边AE的长度为6，边BC的长度为9，边DE的长度为3，求辅助线EF的长度。

解答1由于辅助线EF与边AB平行，所以我们可以利用相似三角形的性质来解决这个问题。

根据题目给出的信息，我们可以得到以下相似三角形比例关系：AE/EF = DE/BC代入已知数值，我们可以得到：6/EF = 3/9进一步计算，得到：EF = 18/3 = 6所以辅助线EF的长度为6。

问题2已知梯形PQRS，边PQ平行于边RS，辅助线TU与边PQ和边RS相交于点T和点U。

如果已知边PT的长度为12，边QT的长度为8，边QU的长度为10，求辅助线TU的长度。

解答2同样地，由于辅助线TU与边PQ平行，我们可以利用相似三角形的性质来解决这个问题。

根据题目给出的信息，我们可以得到以下相似三角形比例关系：PT/TU = QU/QS代入已知数值，我们可以得到：12/TU = 10/(8 + TU)进一步计算，得到：12(8 + TU) = 10TU96 + 12TU = 10TU96 = 2TUTU = 48所以辅助线TU的长度为48。

结论辅助线在解决梯形相关问题时起着关键的作用。

通过合理运用相似三角形的性质，我们可以快速求解辅助线的长度，并解决梯形中的各类问题。

这里提供的两个专题训练问题是基于辅助线与边平行的情况，但在实际应用中，辅助线也可以与其他线段相交。

在解题过程中，要善于分析问题，并运用恰当的方程和几何关系，以达到高效解题的目的。

八年级数学梯形辅助线作法专题练习(含答案)

八年级数学梯形辅助线作法专题练习试卷简介: 全卷共12题，全部为选择题，共120分，要求完成时间为25分钟。

本套试卷是针对已经学习过课文的初二学生以及即将上初二的学生。

通过讲练结合的方式，把梯形的几种常规辅助线作法教会学生，并从中体会到转化的思想，把未知的知识转化为已知的方法去进行解题。

学习建议: 四边形是近几年几何图形中的一个热门考点，围绕四边形展开的各种题型中又以梯形的题目比较多。

遇到梯形的问题，一般都是需要作辅助线进行转化的，通过转化与三角形和平行四边形联系起来，从而把问题简化。

而梯形的辅助线作法多种多样，所以我们需要系统的了解一下梯形辅助线的作法以及在具体背景下的辅助线作法。

本次课主要介绍梯形常见的四种辅助线作法，通过具体题目的讲解，体会梯形的做题技巧。

一、单选题(共12道，每道10分)1.已知等腰梯形的锐角等于60°，它的两底分别为15cm和49cm，则它的腰长为（）A.15cmB.49cmC.34cmD.30cm答案：C解题思路：过上底一点做腰的平行线，构成等边三角形，答案为C试题难度：一颗星知识点：梯形2.如图，在直角梯形ABCD中，∠A＝90°，AB∥DC，AD＝15，AB＝16，BC＝17. 则CD的长是（）A.8B.15C.16D.10答案：A解题思路：过点C做AB的垂线交AB于点F，求出BF,答案为A试题难度：二颗星知识点：直角梯形3.如图在等腰梯形ABCD中，AD∥BC，对角线AC=BC+AD，则∠DBC为（）A.30°B.45°C.60°D.90°答案：C解题思路：过点D作AC的平行线交BC延长线于点E，DE=AC=BE，在等腰梯形中BD=AC,所以△BDE是等边三角形，答案为C易错点：梯形辅助线做法试题难度：三颗星知识点：梯形4.在等腰梯形ABCD中，AD∥BC，AE⊥BC于E，且AE=AD，BC=3AD，则∠B等于（）A.30°B.45°C.60°D.135°答案：B解题思路：由BC=3AD可以求出BE=1/3BC=AD=AE，△AEB是等腰直角三角形，∠B=45°，答案为B试题难度：二颗星知识点：梯形5.梯形ABCD中，AD∥BC，AB=CD=AD=2，∠B=60°，则下底BC的长是( )A.3B.4C.2D.2+答案：B解题思路：过点A作AE∥CD交CD于点E，△ABE是等边三角形，EC=AD=2，BE=2，BC=4，答案为B试题难度：二颗星知识点：梯形6. 等腰梯形两底之差为4，高为2，则等腰梯形的钝角为（）A.150°B.105°C.120°D.135°答案：D解题思路：作一腰的平行线交下底与另一腰所成的三角形是高为2，底边为4的等腰三角形，可以求得底角是45°，则钝角是135°，答案为D试题难度：二颗星知识点：等腰梯形的性质7.梯形两底长分别为14cm和24cm，下底与腰的夹角分别是60°和30°，则较短的腰长为（）A. cmB. cmC. cmD.cm答案：D解题思路：过点D作DE∥AB，可得△DEC是直角三角形，且∠DEC=30°，则CD=1/2EC，EC=BC-AD=10，所以CD=5.答案为D试题难度：二颗星知识点：梯形8.如图，梯形ABCD中，AD//BC，E、F分别是AD、BC的中点，且EF⊥BC．则∠B与∠C应满足（）A.∠B=∠CB.∠B=2∠CC.2∠B=∠CD.∠B+∠C=180°答案：A解题思路：做平行线可得BK=LC,KF=FL,EF⊥BC，可得△EKL是等腰三角形，∠B=∠EKF=∠ELF=∠C,答案为A试题难度：二颗星知识点：梯形9.已知等腰梯形ABCD,周长为40,∠BAD=60°,BD平分∠ABC,则CD的长为（）A.4B.5C.8D.10答案：C解题思路：由题意得，∠A=60°,∠ABD=∠DBC=∠CDB=30°CD=CB=AD,AB=2AD,可求出周长=5AD，AD=8，答案为C试题难度：二颗星知识点：梯形10.如图,等腰梯形ABCD中, AB//DC,AD=BC,且AC⊥BD,CH是高,MN是中位线.则MN与CH之间应满足（）A.MN＞CHB.MN=CHC.MN＜CHD.MN=CH答案：B解题思路：过C做BD的平行线交AB于F,可得△ACF为等腰直角三角形，高线与中线重合，等腰底边AF的一半，AF是上下底边之和。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

例谈梯形中的常用辅助线最重要;平移两腰作出高,延长两腰也是关键;记着平移对角线,上下底和差就出现;如果出现腰中点,就把中位线细心连;上述方法不奏效,过中点旋转成全等;灵活添加辅助线,帮你度过梯形难关;想要易解梯形题,还得注意特题特解;注意梯形割与补,巧变成为□和△.基本图形如下:一、平移1、平移一腰：从梯形的一个顶点作一腰的平行线，把梯形转化为一个三角形和一个平行四边形。

［例1］如图，梯形ABCD的上底AD=3，下底BC=8，腰CD=4，求另一腰AB的取值范围。

AB CDE【变式1】已知：如图,在梯形ABCD中,.求证：.【变式2】已知：如图,在梯形中, .求证：梯形是等腰梯形.2、平移两腰：利用梯形中的某个特殊点，过此点作两腰的平行线，把两腰转化到同一个三角形中。

［例2］如图，在梯形ABCD中，AB//CD，∠D＋∠C=90°，BC=1，AD=3，E、F分别是AB、CD的中点，连接EF，求EF的长。

【变式】如图，在梯形中，，，、为、的中点。

求证：EF=12(CD-AB)3、平移对角线：一般是过上底的一个端点作一条对角线的平行线,与另一底的延长线相交,得到一个平行四边形和三角形,把梯形问题转化为平行四边形和三角形问题解决．【例3】.如图,等腰梯形中, , ,且 ,是高,是中位线,求证：．【变式1】在等腰梯形ABCD中，AD//BC，AD=3，BC=7，BD=25，求证：AC⊥BD。

【变式2】（平移对角线）已知梯形ABCD的面积是32，两底与高的和为16，如果其中一条对角线与两底垂直，则另一条对角线长为_____________ ［例4］在梯形ABCD中，AD//BC，AC=15cm，BD=20cm，高DH=12cm，求梯形ABCD的面积。

二、延长：即延长两腰相交于一点，可使梯形转化为三角形。

［例5］在梯形ABCD中，AD//BC，∠B=50°，∠C=80°，AD=2，BC=5，求CD的长。

【变式1】.如图,在梯形中, , ,梯形的面积与梯形的面积相等．求证： .【变式2】所示，四边形ABCD中，AD不平行于BC，AC＝BD，AD＝BC. 判断四边形ABCD的形状，并证明你的结论.三、作对角线：即通过作对角线，使梯形转化为三角形。

［例6］在直角梯形ABCD中，AD//BC，AB⊥AD，BC=CD，BE⊥CD于点E，求证：AD=DE。

A BCD四、作梯形的高1、作一条高，从底边的一个端点作另一条底边的垂线，把梯形转化为直角三角形或矩形。

［例7］如图，在直角梯形ABCD中，AB//DC，∠ABC=90°，AB=2DC，对角线AC⊥BD，垂足为F，过点F作EF//AB，交AD于点E，求证：四边形ABFE是等腰梯形。

2、作两条高：从同一底边的两个端点作另一条底边的垂线，把梯形转化为两个直角三角形和一个矩形。

［例8］在梯形ABCD中，AD为上底，AB>CD，求证：BD>AC。

【变式1】如图,在梯形中,.求证：.【变式2】所示．ABCD是梯形， AD∥BC， AD＜BC，AB=AC且AB⊥AC，BD=BC，AC，BD交于O.求∠BCD的度数．【变式3】所示．直角梯形ABCD中，AD∥BC，∠A=90°，∠ADC=135°，CD的垂直平分线交BC于N，交AB延长线于F，垂足为M．求证：AD=BF．【变式4】所示．直角梯形ABCD中，∠C=90°，AD∥BC，AD+BC=AB，E是CD的中点．若AD=2，BC=8，求△ABE的面积．【变式5】（过顶点作高）已知AB=BC，AB∥CD，∠D=90°，AE⊥BC．求证：CD=CE．五、作中位线:遇到梯形一腰中点的问题可以作出梯形的中位线,中位线与上、下底都平行,且三线段有数量关系. 或利用“等积变形”,连结梯形上底一端点和另一腰中点,并延长与下底延长线交于一点,构成三角形解决问题．1、已知梯形一腰中点，作梯形的中位线。

［例9］在梯形ABCD中，AD//BC，E是DC的中点，∠AEB=90°，求证：AD＋BC=AB。

【变式1】.已知：梯形 ABCD中AD BC,E为AB中点,且AD＋BC=DC , 求证：DE⊥EC,DE平分∠ADC,CE平分∠BCD．证法2：延长CE与DA延长线交于一点F,过程略．证法3：在DC上截取DF=AD,连结AF、BF、EF解决.【变式2】.已知：如图,在梯形中,是CD的中点.求证：.转化为三角形中位线。

［例10］在梯形ABCD 中，AD//BC ，E 、F 分别是BD 、AC 的中点，求证：（1）EF//AD ；（2）)AD BC (21EF -=【变式1】所示．等腰梯形ABCD 中，AB ∥CD ，对角线AC ，BD 所成的角∠AOB=60°，P ，Q ，R 分别是OA ，BC ，OD 的中点．求证：△PQR 是等边三角形．【变式2】（过一腰中点作底边平行线——构造中位线）已知梯形ABCD 中，AD ∥BC ，∠ABC 的平分线过CD 的中点E ．3、在梯形中出现一腰上的中点时，过这点构造出两个全等的三角形达到解题的目的。

例11、在梯形ABCD 中，AD ∥BC ， ∠BAD=900，E 是DC 上的中点，连接AE 和BE ，求∠AEB=2∠CBE 。

【变式1】如图,梯形中,,为腰的中点,求证：.4.当遇到以上的梯形辅助线添加后不能解决问题时,可以特题特解,结合具体问题中的具体条件,寻求特殊的方法解决问题.比如可将对角线绕中点旋转、利用一腰中点旋转、将梯形补成平行四边形或三角形问题.例12已知：如图5,在梯形ABCD 中,M 、N 分别是BD 、AC 的中点.求证： .【模拟试题】（答题时间：40分钟）1. 若等腰梯形的锐角是60°，它的两底分别为11cm ，35cm ，则它的腰长为__________cm .2. 如图所示，已知等腰梯形ABCD 中，AD ∥BC ，∠B ＝60°，AD ＝2，BC ＝8，则此等腰梯形的周长为（） A. 19 B. 20 C. 21 D. 22**3. 如图所示，AB ∥CD ，AE ⊥DC ，AE ＝12，BD ＝20，AC ＝15，则梯形ABCD 的面积为（） A. 130 B. 140 C. 150 D. 160*4. 如图所示，在等腰梯形ABCD 中，已知AD ∥BC ，对角线AC 与BD 互相垂直，且AD ＝30，BC ＝70，求BD 的长.5. 如图所示，已知等腰梯形的锐角等于60°，它的两底分别为15cm 和49cm ，求它的腰长.AB CDABCDEAB CD6. 如图所示，已知等腰梯形ABCD 中，AD ∥BC ，AC ⊥BD ，AD ＋BC ＝10，DE ⊥BC 于E ，求DE 的长.7. 如图所示，梯形ABCD 中，AB ∥CD ，∠D ＝2∠B ，AD ＋DC ＝8，求AB 的长.**8. 如图所示，梯形ABCD 中，AD ∥BC ，（1）若E 是AB 的中点，且AD ＋BC ＝CD ，则DE 与CE 有何位置关系？（2）E 是∠ADC 与∠BCD 的角平分线的交点，则DE 与CE 有何位置关系？9、如图，已知：在梯形ABCD 中，，AC 、BD 相交于点O. 求证：.10、如图，已知：AD 是的平分线，，，.（1）求证：四边形ADCE 是等腰梯形.（2）若的周长为，求四边形ADCE 的周长.A B CDABCDEABCDAB CDE11、如图2-43所示．在直角三角形ABC 中，E 是斜边AB 上的中点，D 是AC 的中点，DF ∥EC 交BC 延长线于F ．求证：四边形EBFD 是等腰梯形．梯形辅助线专题训练题1、如图，已知在梯形ABCD 中，AB ∥DC ，∠D=60°，∠C=45°，AB=2，AD=4，求梯形ABCD 的面积．2、在梯形ABCD 中，AD//BC ，AB=DC=AD=2， BC=4，求∠B 的度数及AC 的长。

3、如图所示，已知等腰梯形ABCD 中，AD ∥BC ，∠B ＝60°，AD ＝2，BC ＝8，求等腰梯形的周长。

AB CDA B C DAD5、如图所示，在等腰梯形ABCD 中，已知AD ∥BC ，对角线AC 与BD 互相垂直，且AD ＝30，BC ＝70，求BD 的长.6、如图所示，已知等腰梯形的锐角等于60°，它的两底分别为15cm 和49cm ，求它的腰长.7、如图所示，已知等腰梯形ABCD 中，AD ∥BC ，AC ⊥BD ，AD ＋BC ＝10，DE ⊥BC 于E ，求DE 的长.8、已知：如图，梯形ABCD 中，AD ∥BC ，AB=DC ，∠BAD 、∠CDA 的平分线AE 、DF 分别交直线BC 于点E 、F ．求证： CE=BF ．9、如图，在梯形ABCD 中，AD BC ∥，9038BD CD BDC AD BC =∠===，°，，．求AB 的长．10、如图6，在梯形ABCD 中，AD BC ∥，90A ∠=︒，︒=∠45C ，DE=EC ，AB=4,AD=2，求BE 的长．ABCDEAB CDAB CDABCDE1 / 111、已知：如图，梯形ABCD 中，DC ∥AB ，AD=BC ，对角线AC 、BD 交于点O ，∠COD=60°，若CD=3， AB=8，求梯形ABCD 的高．12、已知如图，直角梯形ABCD 中，AD∥BC，AB⊥BC，AD=2，BC=DC=5，点P 在BC 上移动，则当PA+PD 取最小值时，△APD 中边AP 上的高为 .13、如图，在四边形ABCD 中，AC 平分∠BAD ，10CD B C ==，21A B =，9AD =．求AC 的长．12题图B C D O A。

梯形中的常用辅助线总结与对应练习题

合集下载