菲涅耳衍射夫琅和费衍射和傅立叶变换
- 格式:doc
- 大小:2.60 MB
- 文档页数:23








夫琅和费衍射与菲涅尔衍射的联系与区别夫琅和费衍射与菲涅尔衍射是光学中的两个重要概念。
它们都涉及到光的衍射现象,但在具体原理和应用方面存在一些联系和区别。
本文将从深度和广度的角度探讨夫琅和费衍射与菲涅尔衍射的联系与区别,以帮助读者更全面地理解这两个概念。
一、夫琅和费衍射与菲涅尔衍射的联系夫琅和费衍射与菲涅尔衍射的联系在于它们都是描述光波通过障碍物或孔洞产生衍射现象的理论模型。
衍射是光波传播过程中的一种波动现象,当波遇到障碍物或孔洞时,波峰和波谷会通过这些障碍物或孔洞的边缘发生弯曲,并形成衍射图样,即波纹的扩散和干涉现象。
夫琅和费衍射与菲涅尔衍射都是描述这种波动现象的数学模型。
二、夫琅和费衍射与菲涅尔衍射的区别1. 原理:夫琅和费衍射是基于赫兹弹簧原理、弹性理论和波动方程的解,通过求解波动方程中的边界条件来描述光波在障碍物或孔洞上的衍射现象。
菲涅尔衍射是基于菲涅尔半波带原理,考虑光波传播过程中各点的相干衍射贡献,并通过位相积分的方法来计算相干波的干涉效果。
2. 适用范围:夫琅和费衍射主要适用于近场衍射现象的描述,即当光波到达障碍物或孔洞时,场点距离光源较近,衍射图样较为复杂的情况。
菲涅尔衍射则适用于中远场衍射现象的描述,即当光波到达障碍物或孔洞时,场点距离光源较远,衍射图样较为简单的情况。
3. 数学形式:夫琅和费衍射通过波动方程的解,给出了衍射图样的数学表达式。
菲涅尔衍射则通过位相积分的方法,将衍射图样展开为光波的振幅和相位的函数。
4. 应用领域:夫琅和费衍射主要用于研究近场衍射现象,如光学显微镜中的分辨率限制、光纤传输中的损耗与耦合等。
菲涅尔衍射则广泛应用于光学成像、光栅衍射、狭缝衍射等领域。
三、个人观点和理解夫琅和费衍射与菲涅尔衍射是光学中两个重要的衍射理论。
在我的理解中,夫琅和费衍射主要关注近场衍射现象,它通过解析方法给出了复杂的衍射图样的数学表达式。
而菲涅尔衍射则是一种近似的方法,适用于中远场衍射现象,但它的数学形式更为简单,通过位相积分来描述光波的干涉效果。

夫琅和费衍射和菲涅尔衍射的区别夫琅和费衍射和菲涅尔衍射的区别1. 引言在光学领域中,夫琅和费衍射和菲涅尔衍射是两个重要且经常被讨论的概念。
它们都与光的衍射现象有关,但却有着不同的特点和应用。
在本文中,我将深入探讨夫琅和费衍射和菲涅尔衍射的区别,并分析它们在光学领域中的重要性。
2. 夫琅和费衍射的特点夫琅和费衍射是由光波在传播过程中受到不规则边界或障碍物的影响而产生的现象。
特点是:光波传播的路径要经过不规则的边界或障碍物,而且距离较大,观察距离远。
3. 菲涅尔衍射的特点菲涅尔衍射是由光波在通过近场区域时产生的现象,其特点是:光波传播的路径会经过近场区域,观察距离相对较近。
4. 夫琅和费衍射和菲涅尔衍射的区别夫琅和费衍射和菲涅尔衍射在观察的距离、传播路径等方面存在明显的区别。
夫琅和费衍射需要观察距离相对较远,而菲涅尔衍射的观察距离相对较近。
在传播路径上,夫琅和费衍射需要光波经过不规则的边界或障碍物,而菲涅尔衍射则是在通过近场区域时产生。
5. 重要性和应用夫琅和费衍射和菲涅尔衍射在光学领域中具有重要的应用价值。
夫琅和费衍射常用于处理远距离传播的光波,如望远镜、光学天文学等领域;而菲涅尔衍射则常用于近场的光波传播,如显微镜、近程光学成像等领域。
了解它们的区别有助于我们更好地理解和应用这些原理,为光学技术的发展和应用提供更多可能性。
6. 个人观点和理解个人认为,夫琅和费衍射和菲涅尔衍射的区别不仅体现在观察距离和传播路径上,更重要的是其在不同领域的应用。
深入理解和掌握这些区别,对于我们在光学领域中进行研究和实践具有重要的指导意义。
7. 总结通过本文的分析,我们可以清晰地认识到夫琅和费衍射和菲涅尔衍射的区别,并了解它们在光学领域中的重要性和应用。
深入理解这些概念,有助于我们更好地应用光学原理,推动光学技术的发展和创新。
在本文中,我从简到繁地探讨了夫琅和费衍射和菲涅尔衍射的区别,希望能够帮助您更深入地理解这些概念。

菲涅尔衍射实现傅里叶变换
菲涅尔衍射是一种光学现象,利用它可以实现傅里叶变换。
傅里叶变换是信号处理中常用的一种技术,可以将一个信号分解成多个不同频率的正弦波,从而方便信号分析和处理。
菲涅尔衍射的基本原理是在光通过一些具有微小孔洞或缝隙的物体时产生衍射效应,形成衍射图样。
这些图样可以在接收器上形成明暗图形,从而实现信号的分析和处理。
在傅里叶变换中,可以利用其频域特性将信号分解成多个频率不同的正弦波。
具体实现菲涅尔衍射实现傅里叶变换的方法是:将待处理信号作为入射光,通过一个具有微小孔洞或缝隙的物体,进入到一个接收器中,观察衍射图样。
然后,使用适当的算法对衍射图样进行处理,得到信号的频域特性,即傅里叶变换结果。
利用菲涅尔衍射实现傅里叶变换的优点是可以快速且准确地分析信号的频域特性,从而方便信号处理和分析。
同时,该方法也可以应用于其他领域,如光学影像处理、计算机视觉等。
- 1 -。

菲涅尔衍射与夫琅禾费衍射的区别
菲涅尔衍射和夫琅禾费衍射都是光学中常见的现象,它们都涉及到光的衍射现象,但是它们之间有很大的区别。
首先,菲涅尔衍射是指当光线通过一个边缘或孔洞时,光线会发生弯曲和扩散的现象。
菲涅尔衍射产生的弯曲和扩散是由于光线与边缘和孔洞之间的相互作用所致。
而夫琅禾费衍射则是指当光线通过一个有规则的物体表面时,光线会被散射和反射的现象。
夫琅禾费衍射产生的散射和反射是由于光线与物体表面的微小结构相互作用所致。
其次,菲涅尔衍射和夫琅禾费衍射所涉及的物理原理也不同。
菲涅尔衍射是基于菲涅尔光学原理,即光波在边缘或孔洞处的传播是波动性质导致的。
而夫琅禾费衍射是基于夫琅禾费原理,即光波在物体表面的反射和散射是其微结构导致的。
最后,菲涅尔衍射和夫琅禾费衍射的应用也不同。
菲涅尔衍射常用于光学器件中,如光栅、棱镜等。
而夫琅禾费衍射则广泛应用于光学成像领域,如显微镜、望远镜等。
综上所述,菲涅尔衍射和夫琅禾费衍射虽然都涉及到光的衍射现象,但是其产生的机制、原理和应用都有很大的区别。
了解这些区别可以更好地理解它们的应用和掌握光学领域的相关知识。
- 1 -。

菲涅耳衍射、夫琅和费衍射和傅立叶变换利用基尔霍夫或瑞利-索末菲衍射公式计算衍射光场复振幅分布虽然准确, 但是在计算积分时存在数学上的困难。
在一定条件下对瑞利-索末菲衍射公式进行近似, 便可以将衍射现象划分为两种类型——菲涅耳衍射和夫琅和费衍射, 也称近场衍射与远场衍射。
§4-1 菲涅耳衍射夫琅和费衍射的划分先简单分析一下单色光经过衍射小孔后的衍射现象。
下图表示一个单色平面波垂直照射到圆孔Σ上(圆孔直径大于波长)的情形。
若在离Σ很近的K1处观察透过的光, 将看到边缘比较锐利的光斑, 其形状、大小和圆孔基本相同, 可看作是圆孔的投影。
这时光的传播可看作是直线进行的。
若距离再远些, 例如在K2处, 将看到一个边缘模糊的略大的圆光斑, 光斑内有一圈圈的亮暗环, 这时光斑已不能看作是圆孔的投影了。
随着距离的增大, 光斑范围将不断扩大, 但光斑中圆环数目则逐渐减小(如K3处的情况), 而且环纹中心的明暗也表现为交替出现。
当观察平面距离很远时, 如在K4处, 将看到一个较大的中间亮, 边缘暗, 且在边缘外有较弱的亮暗交替的光斑。
此后观察距离再增大时, 只是光斑扩大, 但光斑形状不变。
通常菲涅耳衍射指近场衍射, 夫琅和费衍射指远场衍射。
下面我们根据瑞利-索末菲衍射公式来讨论远和近的范围是怎样划分的。
考虑无限大的不透明屏上的一个有限孔径Σ对单色光的衍射。
设平面屏有直角坐标系(x1, y1), 在平面观察区域有坐标系(x, y), 两者坐标平行, 相距z 。
一、 菲涅耳衍射(近场衍射)在第三章里我们已经得到开孔的瑞利-索末菲衍射公式是⎰⎰∑=dS K r e P U j P U jkr)()(1)(10θλ在图所示的坐标系下, 上式可以写为⎰⎰∑-+-+-+-+=1121212)()(110)()()(),(1),(21212dy dx K y y x x z ey x U j y x U y y x x z jk θλ假设观察屏和衍射屏的距离z 远远大于Σ的线度和观察范围的线度, 那么在z 轴附近1)(≈θK}8])()[(2)()(1{])()(1[)()(4221212212121212121212 +-+-+-+-+=-+-+=-+-+=z y y x x z y y x x z zy y z x x z y y x x z r的情况下, 忽略二阶以上小量, 有]2)()(1{)()(2212121212z y y x x z y y x x z r -+-+≈-+-+=所以⎰⎰⎰⎰⎰⎰⎰⎰∑-+-∑-+-+∑-+-+∑-+-+=≈-+-+≈-+-+=112)()(11011]2)()(1[1101122121]2)()(1[1101121212)()(1102121221212212121212),(1),(1]2)()(1[),(1)()()(),(1),(dy dx e y x U e jz dy dx e y x U jz dy dx z y y x x z ey x U j dy dx K y y x x z ey x U j y x U zy y x x jkjkzz y y x x jkz zy y x x jkz y y x x z jk λλλθλ这一近场近似公式称为菲涅耳衍射公式。

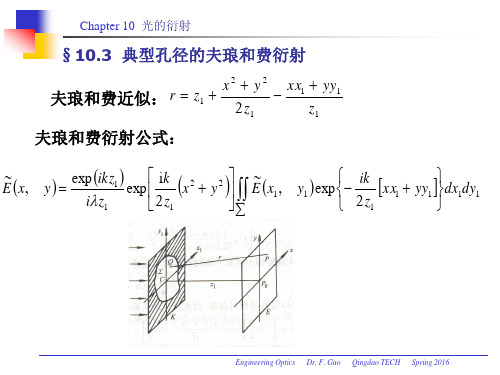


§ 5.2 夫琅和费光栅衍射的傅里叶频谱分析一.屏函数的傅里叶变换1.周期性屏函数的傅里叶变换单缝、圆孔或者光栅,都是使入射波的波前改变,其作用可以用屏函数表示。
有一类应用广泛的衍射屏是衍射光栅,即具有周期性空间结构的衍射屏。
衍射屏具有空间的周期性,而波也具有空间的周期性,即衍射屏函数和复振幅都是空间的周期性函数,那么一定可以从数学上得到新的处理方法。
前面说过的反射、透射或闪耀光栅,可以认为是"黑白型"的。
即一部分使光全部透射或反射、另一部分全部不透光。
是典型的振幅型衍射屏,其屏函数表示为,X方向的透过率表示为其周期性表示为,d为最小的空间周期,即空间周期。
空间频率为。
如果透过率的变化是三角函数形式,即余弦或正弦型的,称为正弦光栅。
如果光栅刻线与y轴平行,则其透过率在X方向作周期性变化,周期为d,空间频率为f,f=1/d。
其屏函数可以写成。
平行光正入射,由于,则透射波的复振幅为。
而,所以,即,透射波实际上变为三列波关于波的方向,为平面波,其波矢在x方向的分量为,方向角为,其余两列波的方向角分别为,。
f为空间频率。
一列波,其空间频率越大,在X方向的波矢分量越大,即对于光轴的角度越大。
所以,对于有限大小的通光孔径,总是空间频率小的波可以通过,空间频率大的波不能通过。
这就是空间滤波的原理。
,0级波,方向,+1级波,方向,-1级波,方向对于一般的周期性的屏函数,可以用傅里叶级数将其展开为一系列正弦和余弦函数的和。
即,,其中,是基频。
或者,,,。
或者,傅里叶系数可以直接求出,的集合为傅里叶频谱,对于周期性的屏函数,的取值是分立的,非周期性的屏函数,的取值为连续的。
对于任何形式的衍射屏或物体,都可以将其看成是一系列空间频谱的叠加。
单色平面波照射到这些物体上,则分解成为一系列向不同方向出射的单色平面波,或者是分立的,或者是连续的。
每一个空间频谱代表一个衍射波。
如果用透镜将不同方向的衍射波汇聚到其像方焦平面的不同位置,得到一系列的衍射斑,则焦平面就是原图像的傅里叶频谱面。
第四章菲涅耳衍射、夫琅和费衍射和傅立叶变换利用基尔霍夫或瑞利-索末菲衍射公式计算衍射光场复振幅分布虽然准确,但是在计算积分时存在数学上的困难。
在一定条件下对瑞利-索末菲衍射公式进行近似,便可以将衍射现象划分为两种类型——菲涅耳衍射和夫琅和费衍射,也称近场衍射与远场衍射。
§4-1 菲涅耳衍射夫琅和费衍射的划分先简单分析一下单色光经过衍射小孔后的衍射现象。
下图表示一个单色平面波垂直照射到圆孔Σ上(圆孔直径大于波长)的情形。
若在离Σ很近的K1处观察透过的光,将看到边缘比较锐利的光斑,其形状、大小和圆孔基本相同,可看作是圆孔的投影。
这时光的传播可看作是直线进行的。
若距离再远些,例如在K2处,将看到一个边缘模糊的略大的圆光斑,光斑内有一圈圈的亮暗环,这时光斑已不能看作是圆孔的投影了。
随着距离的增大,光斑范围将不断扩大,但光斑中圆环数目则逐渐减小(如K3处的情况),而且环纹中心的明暗也表现为交替出现。
当观察平面距离很远时,如在K4处,将看到一个较大的中间亮,边缘暗,且在边缘外有较弱的亮暗交替的光斑。
此后观察距离再增大时,只是光斑扩大,但光斑形状不变。
通常菲涅耳衍射指近场衍射,夫琅和费衍射指远场衍射。
下面我们根据瑞利-索末菲衍射公式来讨论远和近的范围是怎样划分的。
考虑无限大的不透明屏上的一个有限孔径Σ对单色光的衍射。
设平面屏有直角坐标系(x1,y1),在平面观察区域有坐标系(x,y),两者坐标平行,相距z。
一、 菲涅耳衍射(近场衍射)在第三章里我们已经得到开孔的瑞利-索末菲衍射公式是⎰⎰∑=dS K re P U j P U jkr)()(1)(10θλ 在图所示的坐标系下,上式可以写为⎰⎰∑-+-+-+-+=1121212)()(110)()()(),(1),(21212dy dx K y y x x z ey x U j y x U y y x x z jk θλ 假设观察屏和衍射屏的距离z 远远大于Σ的线度和观察范围的线度,那么在z 轴附近1)(≈θK又}8])()[(2)()(1{])()(1[)()(4221212212121212121212 +-+-+-+-+=-+-+=-+-+=zy y x x z y y x x z zy y z x x z y y x x z r},,,{11y x y x z >>的情况下,忽略二阶以上小量,有]2)()(1{)()(2212121212zy y x x z y y x x z r -+-+≈-+-+= 所以⎰⎰⎰⎰⎰⎰⎰⎰∑-+-∑-+-+∑-+-+∑-+-+=≈-+-+≈-+-+=112)()(11011]2)()(1[1101122121]2)()(1[1101121212)()(1102121221212212121212),(1),(1]2)()(1[),(1)()()(),(1),(dy dx e y x U e jz dy dx e y x U jz dy dx zy y x x z ey x U j dy dx K y y x x z ey x U j y x U zy y x x jk jkz z y y x x jkz z y y x x jkz y y x x z jk λλλθλ这一近场近似公式称为菲涅耳衍射公式。
使以上近似成立的观察区称菲涅耳衍射区。
使菲涅耳衍射公式成立的条件是πλπϕ28])()[(28])()[(32max212132max 2121<<-+-=-+-=∆zy y x x z y y x x k 即32max 2121])()[(121y y x x z -+->>λ二、 夫琅和费衍射(远场衍射)菲涅耳衍射公式是⎰⎰⎰⎰∑+-++-∑-+-=≈112])(21[])(21[110112)()(110211221122121),(1),(1),(dy dx e y x U e jz dy dx ey x U e jz y x U zyy y y y x x x x x jk jkzzy y x x jk jkzλλ如果我们的观察区域远远大于衍射孔线度,即max 1max 1||||,||||y y x x >>>>,那么上式又可进一步近似为⎰⎰⎰⎰∑+-++∑--+=≈11)(110)2(1122211011221122),(1),(1),(dy dx ey x Ue jz dy dx e y x U e jz y x U zyy xx jkzy x z jk zyy xx y x jkjkzλλ这样我们对菲涅耳衍射公式的进一步近似称远场近似,得到的衍射公式称为夫琅和费衍射公式,这一积分公式相对菲涅耳衍射公式在数学上又简单了一些。
对应的衍射区域称夫琅和费衍射区。
容易看出,满足夫琅和费衍射的条件是πλπ22)(22)(max 2121max 2121<<+=+zy x z y x k即λ2)(max2121y x z +>>这是一个很强的条件,比如当λ=600nm ,孔径为直径2mm 时,要观察夫琅和费衍射,观察位置必须在远远大于1666mm 的地方。
实际中,往往用102)(22max 21212121πλπ=+=+z y x z y x k ,即λmax 2121)(10y x z +=来确定出现夫琅和费衍射的位置。
§4-2 几种典型的夫琅和费衍射在无限远处观察的衍射是严格的夫琅和费衍射,用一正透镜在后焦面上观察的衍射就是这种情况。
夫琅和费衍射在分析光学仪器的极限分辨本领时有着重要的意义。
夫琅和费衍射计算较为简单,同时它与傅立叶变换有着直接的联系,为此我们有必要进行专门的讨论。
我们已经得到夫琅和费衍射公式是⎰⎰⎰⎰∞∞-+-++∑+-++=≈11)(2110)2(11)(110)2(11221122),(1),(1),(dy dx ey x Ue jz dy dx ey x Uejz y x U y zyx z x j zy x z jk zyy xx jkzy x z jk λλπλλ如果令zyf z x f y x λλ==,,并根据傅立叶变换的定义,则 ),(1)],([1),(1),(0)2(110)2(11)(2110)2(22221122y x zy x z jk zy x z jk y zy x z x j zy x z jk f f G e jz y x U e jz dy dx ey x Uejz y x U ++++∞∞-+-++===⎰⎰λλλλλπF所以观察屏上的光强分布20222|),(|1|),(|),(y x f f G z y x U y x I λ== 可以看出,观察屏上的衍射花样形状主要由),()],([0110y x f f G y x U =F 决定。
下面利用)],([1),(110)2(22y x U e jz y x U zy x z jk F ++=λ分析几种典型的夫琅和费衍射。
一、 矩孔的夫琅和费衍射设矩孔的边长分别为L x ,L y ,在单位振幅的平行光垂直照明的情况下,衍射屏后表面的复振幅与屏的透过率函数是相等的,即)(rect )(rect ),(),(11110yx L y L x y x t y x U == 而)(sinc )(sinc )](rect )(rect [11f L f L L L L yL x x y x x y x yx =F二、]2)2(2[82)()2(12)()2(1)]2/([1)]([1)(12)2(12)2(12)2(1)2(10)2(22222zklr z klr J jzkl e z lr z lr J l e jz l l J l e jz l r circ e jz r U e jz r U zr z jk z r z jk z r z jk zr z jk zr z jk +++++=====λλπλρρπλλλB B其图形如下观察屏处的强度分布21222])2(2[)8(|)(|)(klr z klr J zkl r U r I == 其图形如下可以看出,中央有一强度远远高于其它条纹的亮斑(这一亮斑叫爱里斑),中央亮斑的半径Dlzr 122.122.1λλ==,而D 就是光学仪器的相对孔径,D 越大,亮斑的半径越小,也就是由于衍射产生的象模糊越小,光学仪器的分辨本领越高。
三、 正弦型振幅光栅的夫琅和费衍射l ×l 正方形正弦型振幅光栅的复振幅透过率为)(rect )(rect )]2sin(221[),(111011lyl x x f m y x t π+=方孔内沿x 1方向按正弦规律变化,对同一x 1值,透过率不因y 1变化而变化,光栅的空间频率为f 0,m 是小于1的正数。
正弦型振幅光栅的透过率示意如图。
则夫琅和费衍射的复振幅分布为)}()()]2sin(221{[1)],([1),(1110)2(11)2(2222ly rect l x rect x f me jz y x t e jz y x U zy x z jk zy x z jk πλλ+==++++F F而)}(sinc )]([sinc )(sinc )]([sinc {4)(sinc )(sinc 2)}(sinc )]([sinc )(sinc )]([sinc {4)(sinc )(sinc 2)]([sinc )]([sinc })],(),([4),(21{)](sinc )(sinc [)]},(),([4),(21{)]()([)]2sin(221[)}()()]2sin(221{[0022002220020*********zy l f z x l z y l f z x l j m l z ly z lx l lf f f l lf f f l j m l lf lf l d d f l f l l f f j mlf lf l f f f f f f j mf f l y rect l x rect x f mly rect l x rect x f my x y x y x y x y x y x y x y x λλλλλληξηξηξδηξδηξδδδδππ+--+=+--+=--+--+=*+--+=*+=+⎰⎰∞∞-F F F所以观察面上的复振幅)}}(sinc )]([sinc )(sinc )]([sinc {4)(sinc )(sinc 2{1),(0022)2(22zyl f z x l z y l f z x l j m l zly z lx l ejz y x U zy x z jk λλλλλλλ+--+=++观察面上的光强度分布)]([sinc )]([sinc )(sinc ){(sinc )()}(sinc )]([sinc )(sinc )]([sinc )]([sinc 2)(sinc )]([sinc {)4()(sinc )(sinc )2()}(sinc )]([sinc )(sinc )]([sinc {)4()(sinc )(sinc )2(),(),(),(022202222222202200202222222200222222f z x l m f x l m lx ly l z yl f z x l z y l f z x l f z x l z y l f z x l z m l z ly z lx z l z y l f z x l z y l f z x l z m l zlyz lx z l y x U y x U y x I -++-+=+++---+=+--+==*λλλλλλλλλλλλλλλλλλλλ),(y x I 注意分)]0f 最大的点在0zf x λ=,使)]([sinc 0f zxl +λ最大的点在0zf x λ-=,两者相距02zf x λ=∆。