五年级下册数学第三单元知识归纳

1、我们周围有许多物体的形状都是长方体或正方体（正方体也叫立方体）2、长方体有（6）个面，相对的面（形状完全相同），（面积相等）；有（12）条棱，相对的棱（长度相等），可以分为三组，每组（4）条；有（8个）顶点。

3、正方体有（6）个面，每个面都是（正方形，并且形状完全相同）；有（12）条棱，每条棱（长度都相等）。

4、相交于一个顶点的三条棱的长度分别叫做长方体的长、宽、高。

5、一个长方体，如果它有两个面是正方形，那么另外四个面是（长方形，并且形状完全相同）。

6、正方体是特殊的长方体，正方体可以看成是长、宽、高都相等的长方体。

7、长方体的棱长和=（长+宽+高）*4长=长方体的棱长和/4-宽-高宽=（）高=（）8、长方体或正方体（6）个面的（总面积），叫做它的（表面积）。

9、长方体的表面积=长*宽*2+长*高*2+宽*高*2长方体的表面积=（长*宽+长*高+宽*高）*210、正方体的表面积=棱长*棱长*6 棱长*棱长=正方体的表面积/6（注意：做题的时候看清题目，看到底需要计算几个面的面积。

求长方体的表面积必须知道长方体的（长），（宽），（高），所以在做题时我们就要想办法找出长方体的（长），（宽），（高），然后再看它们单位相不相同，不同就需要转换单位。

）11、物体所占空间的大小叫做物体的体积。

常用的体积单位有（立方厘米），（立方分米），（立方米），可以分别写成（cm3），（dm3），（m3）。

棱长是1cm的正方体，体积是1 cm3（一个手指尖的体积大约是1 cm3）棱长是1dm的正方体，体积是1dm3（粉笔盒的体积大约是1dm3）棱长是1m的正方体，体积是1 m3长方体的体积=长*宽*高正方体的体积=棱长*棱长*棱长正方体与长方体体积的统一公式=底面积*高注：在解决长方体、正方体表面积、体积应用问题时要注意以下几点。

（1）认真审题，辨别所需解决的问题与什么有关。

即是什么形体，与表面积有关还是与体积有关；（2）找准关系式，计算中记清相关公式；（3）计算中，要对照公式所需条件一一确认。

北师大版五年级数学下册重点知识归纳北师大版五年级数学下册重点知识点归纳第一单元：分数加减法1.异分母分数相加减：先通分，化成分母相同的分数，再按照同分母分数相加减的方法进行计算。

计算结果能约分的要约分。

2.分数方程的计算方法与整数方程的计算方法一致，在计算过程中要注意统一分数单位。

3.分数加减混合运算的运算顺序和整数加减混合运算的运算顺序相同。

在计算过程中，整数的运算律对分数同样适用。

4.小数化成分数的方法：将小数化成分母是10、100、1000…的分数，能约分的要约分。

具体方法是：看有几位小数，就在1后边写几个做分母，把小数点去掉的部分做分子，能约分的要约分。

5.分数化成小数的方法：用分子除以分母所得的商即可，除不尽时通常保留三位小数。

6.在分数化成小数时，如果分母只含有2或5的质因数，这个分数能化成有限小数。

如果含有2或5以外的质因数，这个分数就不能化成有限小数。

第二单元：长方体（一）1.正方体是特殊的长方体。

因为正方体可以看成是长、宽、高都相等的长方体。

2.长方体的棱长总和=（长+宽+高）×4或者是长×4+宽×4+高×4.已知长方体棱长总和以及长、宽、高三项中的两项，求另一项，用“棱长总和÷4－已知的两项”。

3.正方体的棱长总和=棱长×12.已知正方体棱长总和，求棱长，用“棱长总和÷12”。

4.长方体的表面积=长×宽×2 +长×高×2 +宽×高×2=（长×宽＋长×高＋宽×高）×2.正方体的表面积=棱长×XXX×6.5.求露在外面的面的面积=一个面的面积×露在外面的面的个数。

6.正方体展开共有11种，其中1-4-1型6个，2-3-1型3个（一个“探头”），2-2-2型1个楼梯形，3-3型1个两个“探头”。

小学五年级下册数学各单元重点知识点整理归纳小学五年级下册数学各单元重点知识点整理归纳在平日的学习中，看到知识点，都是先收藏再说吧！知识点就是学习的重点。

还在为没有系统的知识点而发愁吗？下面是店铺帮大家整理的小学五年级下册数学各单元重点知识点整理归纳，供大家参考借鉴，希望可以帮助到有需要的朋友。

第一单元：图形的变换1、轴对称的意义：把一个图形沿着某一条直线对折，如果它能够与另一个图形完全重合，那么就说这两个图形成轴对称；这条直线就是对称轴。

两个图形完全重合时的点叫做对应点；互相重合的角叫做对应角，互相重合的线段叫做对应线段。

2、轴对称的性质：对应点到对称轴的距离相等。

3、轴对称的特征：沿对称轴对折，对应点、对应线段、对应角重合。

旋转1、旋转的意义：物体绕着某一点运动，这种运动叫做旋转。

2、图形旋转方向：钟表中指针的运动方向成为顺时针旋转；反之，称逆时针旋转。

3、图形旋转的性质：图形绕着某一点旋转一定的度数，图形中的对应点、对应线段都旋转相应的度数，相对应的点到旋转点的距离相等，对应角相等。

4、图形旋转的特征：图形旋转后，形状、大小都没有发生变化，只是位置变了。

设计图案的基本方法1、设计图形的基本方法：利用平移、旋转或对称，可以设计简单而美丽的图案2、运用平移设计图案的方法：（1）选好基本图形；（2）确定平移的距离；（3）确定平移方向；（4）画出平移后的图形3、运用平旋转计图案的方法：（1）选好基本图形；（2）确定旋转点；（3）定好旋转角度；（4）沿每次旋转后的基本图形的边缘画图。

4、运用对称设计图案的方法：（1）选好基本图形；（2）定好对称轴；（3）画出基本图形的对称图形。

第二单元：因数与倍数因数和倍数1、因数和倍数的意义：如果a×b=c（a、b、c都不为0的整数），那么a、b就是c的因数，c就是a、b的倍数。

2、数与倍数的关系：因数和倍数是两个不同的该概念，但又是一对相互依存的概念，不能单独存在。

五年级下册数学知识点归纳总结第一单元图形的变换第二单元因数和倍数第三单元长方体和正方体1、由6个长方形（特殊情况有两个相对的面是正方形）围成的立体图形叫做长方体。

两个面相交的边叫做棱。

三条棱相交的点叫做顶点。

相交于一个顶点的三条棱的长度分别叫做长方体的长、宽、高。

长方体特点：（1）有6个面，8个顶点，12条棱，相对的面的面积相等，相对的棱的长度相等。

（2）一个长方体最多有6个面是长方形，最少有4个面是长方形，最多有2个面是正方形。

2、由6个完全相同的正方形围成的立体图形叫做正方体（也叫做立方体）。

正方体特点：3、长方体、正方体有关棱长计算公式：长方体的棱长总和=（长+宽+高）×4＝长×4+宽×4+高×4 L=（a＋b＋h）×4长=棱长总和÷4－宽－高a=L÷4－b－h宽=棱长总和÷4－长－高b=L÷4－a－h高=棱长总和÷4－长－宽h=L÷4－a－b正方体的棱长总和=棱长×12L=a×12正方体的棱长=棱长总和÷12a=L÷124、长方体或正方体6个面和总面积叫做它的表面积。

长方体的表面积=（长×宽＋长×高＋宽×高）×2S=2（ab＋ah＋bh）无底（或无盖）长方体表面积= 长×宽＋（长×高＋宽×高）×2S=2（ab＋ah＋bh）－abS=2（ah＋bh）＋ab无底又无盖长方体表面积=（长×高＋宽×高）×2S=2（ah＋bh）贴墙纸正方体的表面积=棱长×棱长×6 S=a×a×6 用字母表示：S= 6a²生活实际：油箱、罐头盒等都是6个面游泳池、鱼缸等都只有5个面水管、烟囱等都只有4个面。

注意1：用刀分开物体时，每分一次增加两个面。

人教版五年级数学下册知识点归纳总结第一单元观察物体（三）1、不同角度观察一个物体，看到的面都是两个或三个相邻的面。

2、不可能一次看到长方体或正方体相对的面。

注意点1）这里所说的正面、左面和上面，都是相对于观察者而言的。

2）站在任意一个位置，最多只能看到长方体的3个面。

3）从不同的位置观察物体，看到的形状可能是不同的。

4）从一个或两个方向看到的图形是不能确定立体图形的形状的。

5）同一角度观察不同的立体图形，得到的平面图形可能是相同，也可能是不同的。

6）如果从物体的右面观察，看到的不一定和从左面看到的完全相同。

第二单元因数和倍数1、整除：被除数、除数和商都是自然数，并且没有余数。

整数与自然数的关系：整数包括自然数。

2、因数、倍数：大数能被小数整除时，大数是小数的倍数，小数是大数的因数。

例：12是6的倍数，6是12的因数。

（1）数a能被b整除，那么a就是b的倍数，b就是a的因数。

因数和倍数是相互依存的，不能单独存在。

（2）一个数的因数的个数是有限的，其中最小的因数是1，最大的因数是它本身。

一个数的因数的求法：成对地按顺序找。

（3）一个数的倍数的个数是无限的，最小的倍数是它本身。

一个数的倍数的求法：依次乘以自然数。

（4）2、3、5的倍数特征1）个位上是0，2，4，6，8的数都是2的倍数。

2）一个数各位上的数的和是3的倍数，这个数就是3的倍数。

3）个位上是0或5的数，是5的倍数。

4）能同时被2、3、5整除（也就是2、3、5的倍数）的最大的两位数是90，最小的三位数是120。

同时满足2、3、5的倍数，实际是求2×3×5=30的倍数。

5）如果一个数同时是2和5的倍数，那它的个位上的数字一定是0。

3、自然数按能不能被2整除来分：奇数、偶数。

奇数：不能被2整除的数。

叫奇数。

也就是个位上是1、3、5、7、9的数。

偶数：能被2整除的数叫偶数（0也是偶数），也就是个位上是0、2、4、6、8的数。

最小的奇数是1，最小的偶数是0.关系：奇数+、- 偶数=奇数奇数+、- 奇数=偶数偶数+、-偶数=偶数。

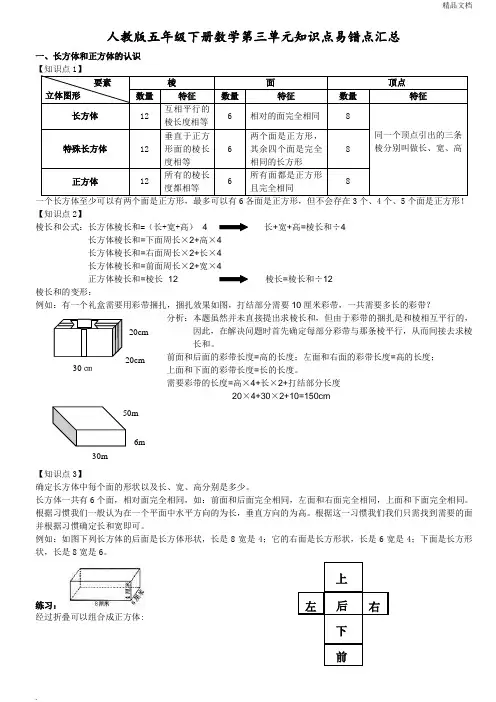
人教版五年级下册数学第三单元知识点易错点汇总一、长方体和正方体的认识 要素 立体图形棱面 顶点数量 特征 数量 特征数量 特征长方体12互相平行的棱长度相等 6相对的面完全相同 8同一个顶点引出的三条棱分别叫做长、宽、高特殊长方体 12 垂直于正方形面的棱长度相等 6 两个面是正方形，其余四个面是完全相同的长方形 8正方体 12 所有的棱长度都相等6 所有面都是正方形且完全相同8一个长方体至少可以有两个面是正方形，最多可以有6各面是正方形，但不会存在3个、4个、5个面是正方形！ 【知识点2】棱长和公式：长方体棱长和=（长+宽+高）×4 长+宽+高=棱长和÷4 长方体棱长和=下面周长×2+高×4 长方体棱长和=右面周长×2+长×4 长方体棱长和=前面周长×2+宽×4正方体棱长和=棱长×12 棱长=棱长和÷12 棱长和的变形：例如：有一个礼盒需要用彩带捆扎，捆扎效果如图，打结部分需要10厘米彩带，一共需要多长的彩带？分析：本题虽然并未直接提出求棱长和，但由于彩带的捆扎是和棱相互平行的，因此，在解决问题时首先确定每部分彩带与那条棱平行，从而间接去求棱长和。

前面和后面的彩带长度=高的长度；左面和右面的彩带长度=高的长度；上面和下面的彩带长度=长的长度。

需要彩带的长度=高×4+长×2+打结部分长度 20×4+30×2+10=150cm【知识点3】确定长方体中每个面的形状以及长、宽、高分别是多少。

长方体一共有6个面，相对面完全相同，如：前面和后面完全相同，左面和右面完全相同，上面和下面完全相同。

根据习惯我们一般认为在一个平面中水平方向的为长，垂直方向的为高。

根据这一习惯我们我们只需找到需要的面并根据习惯确定长和宽即可。

例如：如图下列长方体的后面是长方体形状，长是8宽是4；它的右面是长方形状，长是6宽是4；下面是长方形状，长是8宽是6。

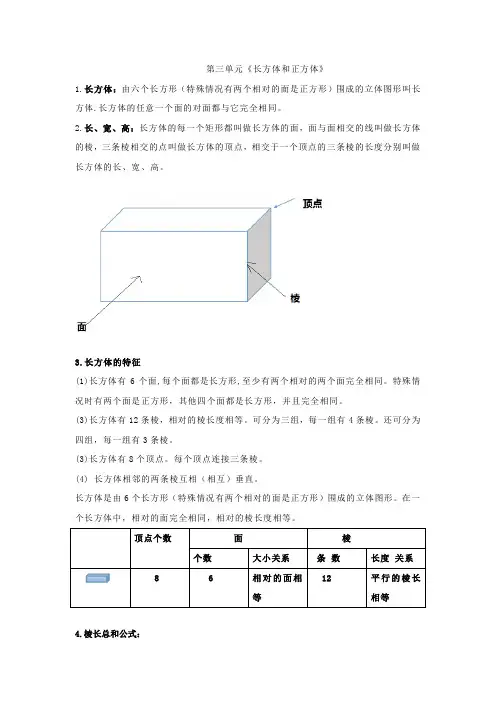
第三单元《长方体和正方体》1.长方体：由六个长方形（特殊情况有两个相对的面是正方形）围成的立体图形叫长方体.长方体的任意一个面的对面都与它完全相同。

2.长、宽、高：长方体的每一个矩形都叫做长方体的面，面与面相交的线叫做长方体的棱，三条棱相交的点叫做长方体的顶点，相交于一个顶点的三条棱的长度分别叫做长方体的长、宽、高。

3.长方体的特征(1)长方体有6个面,每个面都是长方形,至少有两个相对的两个面完全相同。

特殊情况时有两个面是正方形，其他四个面都是长方形，并且完全相同。

(3)长方体有12条棱，相对的棱长度相等。

可分为三组，每一组有4条棱。

还可分为四组，每一组有3条棱。

(3)长方体有8个顶点。

每个顶点连接三条棱。

(4) 长方体相邻的两条棱互相（相互）垂直。

长方体是由6个长方形（特殊情况有两个相对的面是正方形）围成的立体图形。

在一个长方体中，相对的面完全相同，相对的棱长度相等。

顶点个数面棱个数大小关系条数长度关系8 6 相对的面相等 12 平行的棱长相等4.棱长总和公式：长方体棱长总和=4条长+4条宽+4条高＝（长+高+宽）×4宽=棱长之和÷4－长－高长＝棱长之和÷4－宽－高高＝棱长之和÷4－宽－长二、正方体的认识：1. 正方体的认识：正方体是由6个完全相同的正方形围成的立体图形。

正方体有6个面，12条棱，8个顶点，每个面都是正方形，面积都相等。

每条棱的长度都相等。

正方体的长、宽、高都相等，统称棱长。

2.长方体和正方体的关系：正方体是一种特殊的长方体。

3．正方体棱长之和：棱长×１２=棱长之和棱长之和÷１２＝棱长4.长方体的表面积（1）长方体和正方体6个面的总面积，叫做它的表面积。

（2）表面积计算公式①.因为长方体有“上”、“下”、“前”、“后”、“左”、“右”6个面,相对的2个面相等，所以先算上下两个面，再算前后两个面，最后算左右两个面。

②长方体的表面积=（长×宽＋长×高＋宽×高）×2用字母表示： S=（ab＋ah＋bh）×2长方体表面积＝（长×宽＋长×高＋宽×高）×2设一个长方体的长、宽、高分别为a、b、c，则它的表面积S：S = 2ab + 2bc+ 2ca= 2 ( ab + bc + ca)长方体没盖的表面积＝长×宽＋长×高×2 ＋宽×高×2③特殊长方体的表面积（有两个面是正方形）正方形的两个面完全相同，其余四个面完全相同。

第三单元：因数与倍数1、几个非零自然数相乘，每个自然数都叫它们积的因数，积是这几个自然数的倍数。

因数与倍数是相互依存绝不能孤立的存在。

2、一个数最小的因数是1，最大的因数是它本身，一个数因数的个数是有限的。

（找因数的方法：成对的找。

）3、一个数最小的倍数是它本身，没有最大的倍数。

一个数倍数的个数是无限的。

（找一个数倍数的方法：从自然数1、2、3、……分别乘这个数）4、一个数最大的因数等于这个数最小的倍数。

5、按照一个数因数个数的多少可以把非0自然数分成三类①只有自己本身一个因数的1 ②只有1和它本身两个因数的数叫作质数（素数）。

最小的质数是2.在所有的质数中，2是唯一的一个偶数。

③除了1和它本身两个因数还有别的因数的数叫作合数。

（合数至少有 3个因数）最小的合数是4。

按照是否是2的倍数可以把自然数分成两类偶数和奇数。

最小的偶数是0.5、两个数公有的因数，叫做这两个数的公因数，其中最大的一个，叫做这两个数的最大公因数，用符号( ，)。

两个数的公因数也是有限的。

公因数只有1的两个数叫作互质数6、两个数公有的倍数，叫做这两个数的公倍数，其中最小的一个，叫做这两个数的最小公倍数，用符号[ ，]表示。

两个数的公倍数也是无限的。

7、两个素数的积一定是合数。

举例：3×5=15，15是合数。

8、两个数的最小公倍数一定是它们的最大公因数的倍数。

举例：[6，8]=24，(6，8)=2，24是2的倍数。

9、求最大公因数和最小公倍数的方法：（列举法、图示法、短除法......）①倍数关系的两个数，最大公因数是较小的数，最小公倍数是较大的数。

举例：15和5，[15，5]=15，(15，5)=5 ②互质关系的两个数，最大公因数是1，最小公倍数是它们的乘积。

举例：[3，7]=21，(3，7)=1 ③一般关系的两个数，求最大公因数用列举法或短除法，求最小公倍数用大数翻倍法或短除法。

10、质因数：如果一个数的因数是质数，这个因数就是它的质因数。

人教版五年级数学下册知识点班级：姓名：第一单元观测物体1、由几种大小相似旳小正方体摆成旳立体图形，从同一种方向观测，看到旳图形也许是相似旳，也也许是不一样旳。

根据一种方向看到旳图形摆立体图形，有多种摆法。

2、从同一种方向观测物体最多只能看到三个面。

几何视图一般是根据三个方向观测到旳形状进行绘制。

3、根据两个方向观测到旳形状能确定所用小正方体旳个数。

根据三个方向观测到旳形状摆小正方体成果只有一种。

第二单元因数和倍数1、在整数除法中，假如商是整数而没有余数，我们就说被除数是除数旳倍数，除数是被除数旳因数。

因数和倍数是互相依存旳，不能单独存在。

）2、注意：为了以便，在研究因数和倍数时候，我们所说旳数指旳是自然数（一般不包括0）3、找因数旳措施：①乘法②除法；找倍数旳措施：逐次乘自然数。

4、①一种数旳最小因数是1，最大因数是它自身。

一种数旳最小倍数是它自身，没有最大旳倍数。

②一种数旳因数旳个数是有限旳，一种数旳倍数旳个数是无限旳。

一种数旳最大因数和最小倍数是相等旳都是它自身。

③1是所有非0自然数旳因数。

也是任一自然数（0除外）旳最小因数。

④一种数旳因数至少有1个，这个数是1。

⑤一种数旳因数都不不小于等于他自身，一种数旳倍数都不小于等于他自身。

5、因数＜或=它自身、倍数＞或 = 它自身、最大旳因数=最小旳倍数=它自身。

一种数旳倍数一定比它旳因数大这种说法是错误旳。

一种数越大它旳因数个数就越多，一种数越小它旳因数个数就越少。

这种说法是错误旳。

6、2旳倍数特性：个位上是0、2、4、6、8旳数都是2旳倍数。

自然数中，是2旳倍数旳数叫做偶数（0也是偶数），不是2旳倍数旳数叫奇数。

7、5旳倍数特性：个位上是0或5旳数，都是5旳倍数。

8、3旳倍数旳特性：一种数各位上旳数旳和是3旳倍数，这个数就是3旳倍数。

个位上是3、6、9点数都是3旳倍数是错误旳说法。

9、2和5旳倍数特性：个位上是0旳数，既是2旳倍数，也是5旳倍数。