人教版初二上册第一学期数学期末复习《轴对称图形》 (2)

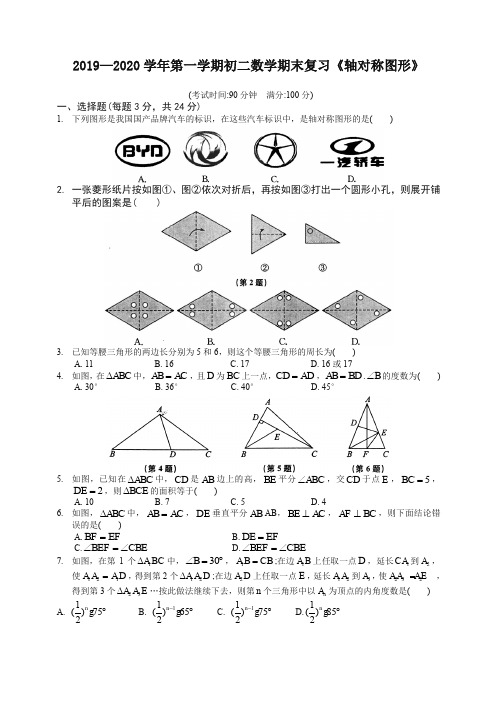
2019—2020学年第一学期初二数学期末复习《轴对称图形》(考试时间:90分钟 满分:100分)一、选择题(每题3分，共24分)1. 下列图形是我国国产品牌汽车的标识，在这些汽车标识中，是轴对称图形的是( )2. 一张菱形纸片按如图①、图②依次对折后，再按如图③打出一个圆形小孔，则展开铺平后的图案是( )3. 已知等腰三角形的两边长分别为5和6，则这个等腰三角形的周长为( ) A. 11 B. 16 C. 17 D. 16或174. 如图，在ABC ∆中，AB AC =，且D 为BC 上一点，CD AD =，AB BD =.B ∠的度数为( ) A. 30° B. 36° C. 40° D. 45°5. 如图，已知在ABC ∆中，CD 是AB 边上的高，BE 平分ABC ∠，交CD 于点E ，5BC =，2DE =，则BCE ∆的面积等于( )A. 10B. 7C. 5D. 46. 如图，ABC ∆中，AB AC =，DE 垂直平分AB AB ，BE AC ⊥，AF BC ⊥，则下面结论错误的是( )A.BF EF =B.DE EF =C.BEF CBE ∠=∠D.BEF CBE ∠=∠7. 如图，在第1个1A BC ∆中，30B ∠=︒，1A B CB =;在边1A B 上任取一点D ，延长1CA 到2A ，使121A A A D =，得到第2个12A A D ∆;在边2A D 上任取一点E ，延长12A A 到3A ，使232AA AE =，得到第3个23A A E ∆…按此做法继续下去，则第n 个三角形中以n A 为顶点的内角度数是( ) A. 1()752n︒g B. 11()652n -︒g C. 11()752n -︒g D.1()852n ︒g8. 如图是1P 、2P 、…、10P 十个点在圆上的位置图，且此十点将圆周分成十等分.今小玉连接12PP 、110PP 、910P P 、56P P 、67P P ，判断小玉再连接下列哪一条线段后，所形成的图形不是轴对称图形?( )9. 下面有五个图形，与其他图形不同的是第 个.10. 如图，在22⨯方格纸中，有一个以格点为顶点的ABC ∆，请你找出方格纸中所有与ABC ∆成轴对称且也以格点为顶点的三角形，这样的三角形共有 个.11. ABC 中，90C ∠=︒，BAC ∠的平分线交BC 于点D ，若4CD =，则点到AB 的距.12. 等腰三角形ABC 中，AB AC =，DE 垂直平分AB ，已知40ADE ∠=︒，则.13. ABC 中，B ∠与C ∠的平分线交于点O ，过点O 作//DE BC ，分别交AB 、AC 于D 、E .若5AB =，4AC =，则ADE ∆的周长是 .14. 如图，CD 与BE 互相垂直平分，AD DB ⊥，70BDE ∠=︒，则CAD ∠= .15. 如图，110BAC ∠=︒，若MP 和NQ 分别垂直平分AB 和AC ，则PAQ ∠的度数是 . 16. 等腰三角形一腰上的高与另一腰的夹角为30°，则它的顶角为 .17. 在44⨯的方格中有五个同样大小的正方形如图摆放，移动其中一个正方形到空白方格中，与其余四个正方形组成的新图形是一个轴对称图形，这样的移法共有 种.18. 如图，AOB ∠是一角度为10°的钢架，要使钢架更加牢固，需在其内部添加一些钢管：EF 、FG GH …，且OE EF FG GH ===……在OA 、OB 足够长的情况下，最多能添加这样的钢管的根数为 .三、解答题(共56分)19. (6分)如图，在由边长为1的小正方形组成的1010⨯的网格中(我们把组成网格的小正方形的顶点称为格点)，四边形ABCD 在直线l 的左侧，其四个顶点A 、B 、C 、D 分别在网格的格点上. (1)请你在所给的网格中画出四边形1111A B C D ，使四边形1111A B C D 和四边形ABCD 关于直线l 对称. (2)在(1)的条件下，结合你所画的图形，直接写出四边形1111A B C D 的面积.20. ( 6分)如图，在ABC ∆中，90C ∠=︒. (1)用圆规和直尺在AC 上作点P ，使点P 到A 、B 的距离相等.(保留作图痕迹，不写作法和证明) (2)当满足(1)的点P 到AB 、BC 的距离相等时，求A ∠的度数.21. (6分)如图，在ABC ∆中，DM 、EN 分别垂直平分AC 和BC ，交AB 于M 、N 两点，DM 与EN 相交于点F .(1)若CMN ∆的周长为15 cm ，求AB 的长. (2)若70MFN ∠=︒，求MCN ∠的度数.22. (6分)如图，在ABC ∆中，点D 、E 分别在边AC A 、AB 上，BD 与CE 交于点O ，给出下列三个条件:①EBO DCO ∠=∠;②BE CD =;③OB OC =.(1)上述三个条件中，由哪两个条件可以判定ABC ∆是等腰三角形? (用序号写出所有成立的情形) (2)请选择(1)中的一种情形，写出证明过程.23. ( 6分)如图，在ABC ∆中，AB AC =，点D 、E 、F 分别在边AB 、BC 、AC 上，且BD CE =，BE CF =，如果点G 为DF 的中点，那么EG 与DF 垂直吗?24. ( 8分)如图，在ABC ∆中，AB AC =, D 、E 是BC 边上的点，连接AD 、AE ，以ADE ∆的边AE 所在直线为对称轴作ADE ∆的轴对称图形'AD E ∆，连接'D C ，若'BD CD =. (1)求证: 'ABD ACD ∆≅∆.(2)若120BAC ∠=︒，求DAE ∠的度数.25. ( 9分)如图①，ABC ∆和CDE ∆均为等腰三角形，AC BC =，CD CE =，AC CD >，ACB DCE ∠=∠且点A 、D 、E 在同一直线上，连接BE .(1)若60ACB ∠=︒，则AEB ∠的度数为 ;线段AD 、BE 之间的数量关系是 .(2)若ACB n ∠=︒，用n 表示AEB ∠并说明理由.(3)如图②，若90ACB DCE ∠=∠=︒, M 是DE 的中点.若7CM =，10BE =，试求AE 的长.(请写全必要的证明和计算过程)26. ( 9分)如图，已知BAD ∆和BCE ∆均为等腰直角三角形，90BAD BCE ∠=∠=︒, M 是DE 的中点，过点E 与AD 平行的直线交射线AM 于点N .(1)当A 、B 、C 三点在同一直线上时(如图①)，求证:M 为AN 的中点. (2)将图①中的BCE ∆绕点B 旋转，当A 、B 、E 三点在同一直线上时(如图②)，求证: ACN ∆为等腰直角三角形.(3)将图①中BCE ∆绕点B 旋转到图③位置时，(2)中的结论是否仍成立?若成立，试证明之;若不成立，请说明理由.参考答案一、1.C 2. C 3.D 4.B 5.C 6.B 7.C 8.D 二、9.③10.5 11.4 12.15 13.9 14.70 15.40°16.60°或120° 17. 13 18.8三、19.(1) 略 (2)13220.(1) 略 (2)30° 21.(1) 15cm (2)40° 22.(1)①②；①③ (2)略 23.23.连接DE 、EF ，证明BDE CEF ∆≅∆，所以DE EF = 因为点G 为DF 的中点，所以EG 与DF 垂直. 24. (1)略(2)因为'ABD ACD ∆≅∆ 所以'BAD CAD ∠=∠所以'120BAC DAD ∠=∠=︒因为以ADE ∆的边AE 所在直线为对称轴作△ADE ∆的轴对称图形'AD E ∆所以1''602DAE D AE DAD ∠=∠=∠=︒ 25. (1)60︒ 相等 (2)AEB n ∠=︒，理由:证明ACD BCE ∆≅∆ 所以CAD CBE ∠=∠ 因为AHC BHE ∠=∠所以AEB ACB n ∠=∠=︒(3)因为CDE ∆是等腰直角三角形，M 是DE 的中点 所以CM DE ⊥，7CM DM == 所以214DE DM ==因为90ACB DCE ∠=∠=︒ 所以ACD BCE ∠=∠ 所以ACD BCE ∆≅∆所以10AD BE ==，CAD CBE ∠=∠ 因为AHC BHE ∠=∠所以90AEB ACH ∠=∠=︒ 所以24AE AD DE =+= 26. (1)证明:因为//EN AD所以MAD MNE ∠=∠，ADM NEM ∠=∠ 因为点M 为DE 的中点 所以DM EM =所以ADM NEM ∆≅∆ 所以AM MN =所以M 为AN 的中点(2)因为BAD ∆和BCE ∆均为等腰直角三角形所以AB AD =，CB CE =，45CBE CEB ∠=∠=︒ 因为//AD NE所以180DAE NEA ∠+∠=︒ 因为90DAE ∠=︒ 所以90NEA ∠=︒ 所以135NEC ∠=︒因为A 、B 、E 三点在同一直线上 所以180135ABC CBE ∠=︒-∠=︒ 所以ABC NEC ∠=∠因为ADM NEM ∆≅∆(已证) 所以AD NE = 因为AD AB = 所以AB NE =所以ABC NEC ∆≅∆所以AC NC =，ACB NCE ∠=∠ 所以90ACN BCE ∠=∠=︒ 所以ACN ∆为等腰直角三角形. (3) ACN ∆仍为等腰直角三角形. 证明：延长AB 交NE 于点F 因为//AD NE ， M 为中点 所以易得ADM NEM ∆≅∆ 所以AD NE = 因为AD AB = 所以AB NE = 因为//AD NE 所以AF NE ⊥在四边形BCEF 中，因为90BCE BFE ∠=∠=︒ 所以360180180FBC FEC ∠+∠=︒-︒=︒ 因为180FBC ABC ∠+∠=︒ 所以ABC FEC ∠=∠ 所以ABC NEC ∆≅∆所以AC NC =，ACB NCE ∠=∠ 所以90ACN BCE ∠=∠=︒ 所以ACN ∆为等腰直角三角形.。

第十三章轴对称
13.1 轴对称（对称点）
轴对称图形：如果一个平面图形沿一条直线折叠，直线两旁的部分能够互相重合。

这条直线就是它的对称轴。

垂直平分线：经过线段中点并且垂直于这条线段的直线。

图形轴对称的性质：如果两个图形关于某条直线对称，那么对称轴是任何一对对应点所连线段的垂直平分线。

线段垂直平分线的性质：垂直平分线上的点到两端的距离相等。

若PA=PB，点C为AB中点，则PC⊥AB或点P在线段AB的垂直平分线上。

13.2 画轴对称图形
先画对称点（过该点画对称轴的垂线，取等长），然后连接对称点，形成轴对称图形。

13.3 等腰三角形
概念：有两边相等的三角形。

性质：等边对等角，三线合一（顶角平分线、底边上的中线、底边上的高）。

判定：等角对等边
等边三角形：三边都相等的特殊的等腰三角形。

三个内角都相等，每个内角60º。

（判定：三个角都相等的三角形；有一个角是60º的等腰三角形。

）
在RtΔ中，如果一个锐角等于30º，那么它所对的直角边等于斜边的一半。

（在RtΔ中，斜边上的中线等于斜边的一半。

）
13.4 课题学习最短路径问题
利用轴对称、平移作出最短路径选择。

（两点之间线段最短）
作者留言：
非常感谢！您浏览到此文档。

为了提高文档质量，欢迎您点赞或留言告诉我文档的不足之处，以便于对该文档进行完善优化，在此本人深表感
谢！祝您天天快乐！。

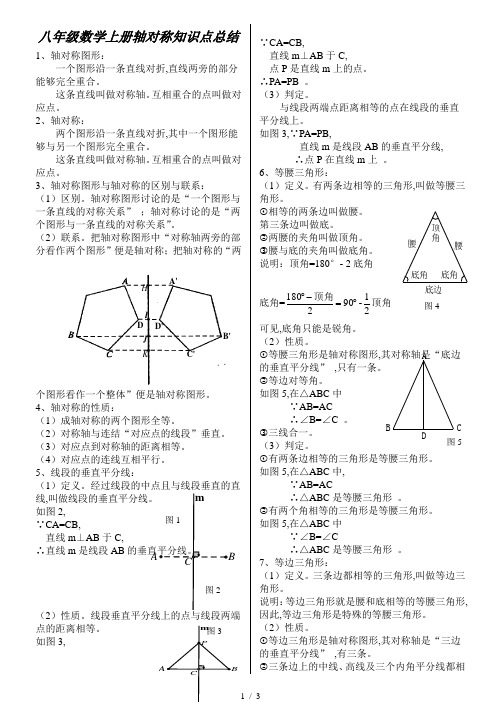
八年级数学上册轴对称知识点总结1、轴对称图形：一个图形沿一条直线对折,直线两旁的部分能够完全重合。

这条直线叫做对称轴。

互相重合的点叫做对应点。

2、轴对称：两个图形沿一条直线对折,其中一个图形能够与另一个图形完全重合。

这条直线叫做对称轴。

互相重合的点叫做对应点。

3、轴对称图形与轴对称的区别与联系：（1）区别。

轴对称图形讨论的是“一个图形与一条直线的对称关系” ；轴对称讨论的是“两个图形与一条直线的对称关系”。

（2）联系。

把轴对称图形中“对称轴两旁的部分看作两个图形”便是轴对称；把轴对称的“两个图形看作一个整体”便是轴对称图形。

4、轴对称的性质：（1）成轴对称的两个图形全等。

（2）对称轴与连结“对应点的线段”垂直。

（3）对应点到对称轴的距离相等。

（4）对应点的连线互相平行。

5、线段的垂直平分线：（1）定义。

经过线段的中点且与线段垂直的直线,叫做线段的垂直平分线。

如图2,∵CA=CB,直线m ⊥AB 于C,∴直线m 是线段AB 的垂直平分线。

（2）性质。

线段垂直平分线上的点与线段两端点的距离相等。

如图3,∵CA=CB,直线m ⊥AB 于C,点P 是直线m 上的点。

∴PA=PB 。

（3）判定。

与线段两端点距离相等的点在线段的垂直平分线上。

如图3,∵PA=PB,直线m 是线段AB 的垂直平分线, ∴点P 在直线m 上 。

6、等腰三角形：（1）定义。

有两条边相等的三角形,叫做等腰三角形。

①相等的两条边叫做腰。

第三条边叫做底。

②两腰的夹角叫做顶角。

③腰与底的夹角叫做底角。

说明：顶角=180°- 2底角底角=顶角顶角21-902180︒=-︒ 可见,底角只能是锐角。

（2）性质。

①等腰三角形是轴对称图形,其对称轴是“底边的垂直平分线” ,只有一条。

②等边对等角。

如图5,在△ABC 中 ∵AB=AC∴∠B=∠C 。

③三线合一。

（3）判定。

①有两条边相等的三角形是等腰三角形。

如图5,在△ABC 中, ∵AB=AC∴△ABC 是等腰三角形 。

八年级上册数学轴对称知识点总结篇1：八年级上册数学轴对称知识点总结八年级上册数学轴对称知识点总结1.对称轴：如果一个图形沿某条直线折叠后，直线两旁的部分能够互相重合，那么这个图形叫做轴对称图形;这条直线叫做对称轴。

2.性质：(1)轴对称图形的对称轴，是任何一对对应点所连线段的垂直平分线。

(2)角平分线上的点到角两边距离相等。

(3)线段垂直平分线上的任意一点到线段两个端点的距离相等。

(4)与一条线段两个端点距离相等的点，在这条线段的垂直平分线上。

(5)轴对称图形上对应线段相等、对应角相等。

3.等腰三角形的性质：等腰三角形的两个底角相等，(等边对等角)4.等腰三角形的顶角平分线、底边上的高、底边上的中线互相重合，简称为“三线合一”。

5.等腰三角形的判定：等角对等边。

6.等边三角形角的特点：三个内角相等，等于60°，7.等边三角形的判定：三个角都相等的三角形是等腰三角形。

有一个角是60°的.等腰三角形是等边三角形有两个角是60°的三角形是等边三角形。

8.直角三角形中，30°角所对的直角边等于斜边的一半。

9.直角三角形斜边上的中线等于斜边的一半。

数学学习方法诀窍1细心地发掘概念和公式很多同学对概念和公式不够重视，这类问题反映在三个方面：一是，对概念的理解只是停留在文字表面，对概念的特殊情况重视不够。

例如，在代数式的概念(用字母或数字表示的式子是代数式)中，很多同学忽略了“单个字母或数字也是代数式”。

二是，对概念和公式一味的死记硬背，缺乏与实际题目的联系。

这样就不能很好的将学到的知识点与解题联系起来。

三是，一部分同学不重视对数学公式的记忆。

记忆是理解的基础。

如果你不能将公式烂熟于心，又怎能够在题目中熟练应用呢?我们的建议是：更细心一点(观察特例)，更深入一点(了解它在题目中的常见考点)，更熟练一点(无论它以什么面目出现，我们都能够应用自如)。

2养成良好的解题习惯要想学好数学，多做题目是难免的，熟悉掌握各种题型的解题思路。

轴对称专题复习讲义 一. 知识要点对称是一个广阔的主题，在艺术和自然两个方面都意义重大，数学则是它的根本. 本次课主要研究以下内容：（1）轴对称图形与轴对称，它们的联系与区别：轴对称图形是对某一个图形而言的；成轴对称是对两个图形而言的，它们的辩证关系：把成轴对称的两个图形看成一个整体，它是轴对称图形；把一个轴对称图形沿对称轴分成两个图形，这两个图形关于这条对称轴对称.（2）线段的垂直平分线的性质：线段的垂直平分线上的点到这条线段两个端点的距离相等。

遇到线段的垂直平分线时，常将垂直平分线上的点与线段的两端点连接.利用轴对称思想添加辅助线段构造全等三角形.证明线段或角相等是我们几何证明的常用方法之一. 二.基本知识点过关测试1.把一个图形沿着某一条直线折叠，如果它能够与 重合，那么就说 关于这条直线（成轴）对称，这条直线叫做 ，折叠后重合的点是 叫做 .如果一个图形沿一直线折叠，直线 能够相互重合，这个图形就叫做 这条直线就是它的对称轴，这时，我们也说 . 2.判断下列是否为轴对称图形，若是请写出对称轴的条数： （1）圆 ；（2）正方形 ；（3）等腰三角形 3.平面直角坐标系中，点A （-2,3）关于y 轴的对称点A 1的坐标是 ，点B （-4,1）关于x 轴的对称点B 1的坐标是 ，点A 1关于一、三象限的角平分线的对称点的坐标是 .知识要点2：线段的垂直平分线的性质：线段的垂直平分线上的点到这条线段两个端点的距离相等. 4.如图，在△ABC 中，AB =AC ，DE 为AB 的中垂线. 且△BEC 的周长为14，BC =6，则AB 的长为 .知识要点3：等腰三角形的性质与判定5.如图，在等腰△ABC 中,AB =AC ，若∠1=∠2，则BD CD ，AD BC6.在等腰三角形中，若一个角为100°，则另两个角为 ，若一个内角为40°，则另两个角为 .7.（1）等腰三角形的腰为10，则底边长x 的范围是 ；若底边长为10，则腰长y 的范围是 .C E B DA（2）等腰三角形的顶角为60°，底边长8cm ，则腰为 .（3）等腰△ABC ，AB =AC ，BD 为AC 边的高，则∠DBC = ∠BAC ；若∠DBA =45°，则∠C = .（4）三角形三内角度数比为1：2：3，它的最短边为5cm ，则最长边为 ；等腰三角形底角为15°，腰长为30cm ，，则此三角形面积为 .知识要点4：等边三角形的性质与判定8.如图，在等边△ABC 中，BD =CE ，AD 与BE 相交于点P ，则∠APE 的度数是 .知识要点5：含30°的特殊三角形9.如图，在△ABC ，∠C =90°，∠B =15°，AB 的垂直平分线交于BC 于点D ，交AB 于点E ，BD =10，则AC = .知识要点6：尺规作图问题10.如图，直线MN 表示一条铁路，A 、B 两点表示铁路旁的两个村庄，要在铁路MN 旁修建一个车站C ，要使A 、B 两个村到车站的距离相等，请确定车站C 的位置11.某地有两所大学和两条相交叉的公路（点M 、N 表示大学AO 、BO 表示公路），现计划修一座物资仓库，希望仓库到两所大学的距离相等，到两条公路的距离也相等.C ED PE AD B EC A A B N MA三. 综合、提高、创新方法与技巧1：利用轴对称解决几何问题【例1】（1）如图，要在燃气管道l上修建一个泵站，分别向A、B两镇供气，泵站修在管道的什么地方，可使所用输气管道最短？你可以在l上找几个点试一试，能发现什么规律？（2）已知∠MON=30°，P为∠MON内一定点，且OP=10cm，A为OM上的点，B为ON上的点，当△P AB的周长取最小值时，请确定A、B点的位置，并求此时的最小周长.方法与技巧2：利用特殊图形的轴对称性（线段的垂直平分线，角平分线）实现边、角的集中【例2】（1）如图，AC=BG，AB，CG垂直平分线交于点F, 求证：∠ABF=∠CGF.（2）如图，在Rt△ABC中，∠ACB=90°，DE垂直平分斜边AB于D，且点E在AB的下方，DE=12AB. ①求证：∠ACE=45°BAlNOFGECBDABDCA②若点E 在AB 的上方，其他条件不变，则①的结论是否还成立？若成立，请证明；若不成立，请说明理由.【例3】如图，在△ABC 中，∠ABC=2∠C ，AD 是角平分线，过BC 的中点M 作AD 的垂线，交AD 的延长线于F ，交AB 的延长线于E ，求证：BE=12BD【练】如图，在△ABC 中，AB >AC ，AD 是BC 上的高线，P 是AD 上一点，试比较PB —PC 与AB —AC的大小.方法与技巧3：截长补短在特殊三角形中的应用 【例4】（1）在△ABC 中，AD ⊥BC 于D ，∠C =2∠B .求证：AC +CD =BD .A CDE BE CD P B AC D B A（2）在△ABC，AD平分∠BAC，AD=AB，CM⊥AD于M，求证：AM=12（AB+AC）【练】如图，在四边形ABCD中，∠B+∠D=180°，AB=AD，∠ACD=60°，求证：AG=AH方法与技巧4：特殊要素法在特殊三角形中的应用【例5】（1）如图，△ABC中，AB=AC，BG⊥BC于B，CH⊥BC于C，过点A的直线l绕点A旋转，交BG、CH于G、H，求证：AG=AH（2）如图，点P为△ABC内一点G，PG垂直平分BC，交点为G，且∠PBC=12∠A，BP、CP 的延长线分别交AC、AB于D、E.求证：BE=CDCMDBADCBACHGBADPEA【例6】如图，△ABC 为等边三角形，D 为AC 所在直线上一点，AE ∥BC ，且满足∠BDE =60°，当D 点分别运动到如图所示情形时. （1）求∠CBD 和∠ADE 的关系；（2）求证：DB =DE ；（3）求AD 、AE 和BC 之间的关系.三. 反馈练习1.如图，四边形EFGH 是一矩形的台球台面，有黑白两球分别位于A 、B 两点位置上，试问：怎样撞击黑球A ，使黑球先碰撞台边EF 反弹后再击中白球B ？2.如图，E 、F 分别是△ABC 的边AB 、AC 上的两定点，在BC 上求一点M 使△MEF 的周长最短.GC B AE C D B A E D B C A C E B D3 如图，A 点的坐标为（4，0），B 点的坐标为（0，4），作∠BAO 的平分线AC 交y 轴于C ，过B 作BD ⊥AC 于D ,求AC ：BD 的值.4 如图，AB =AC ，若∠A =20°，在AB 上取点W ，使AE =BC .求∠BWC 的度数？5.如图，A 、B 两点在直线l 的两侧，在l 上找一点C ，使C 到A ，B 的距离只差最大.6.如图，Rt △ABC 中，CD 是斜边AB 上的高，BE 平分∠ABC 交CD 于F ，CG 平分∠ACD . 求证：BE ⊥CGC BW AB Al C F EB D G A7.如图，∠1=∠2，DA =DB ，AC =12AB ，求证：DC ⊥AC .8.（1）如图，△ABC 中，若AD 平分∠BAC ，AB +BD =AC ，求∠B ：∠C（2）如图，△ABC 中，若AD 平分∠BAC ，∠B =2∠C ，求证：AB +BD =AC9.如图，AM 为△ABC 的角平分线，BD =CE ，NE ∥AM ，求证：N 为BC 中点.C D BAC D B A C D B ACD E A10.如图，在△ABC 中，∠BAC =90°，AD ⊥BC 于D ，∠BCA 的平分线交AD 于O ，交AB 于E ，OF ∥BC ，交AB 于F ，AE =6，AB =18，求EF .11.如图，在四边形ABCD 中，AC 平分∠BAD ，过C 作CE ⊥AB 于E ，并且AE =12（AB +AD ）. 求∠ABC +∠ADC 的度数.12.如图，在△ABC 中，∠ACB =90°，∠BAC =30°，△ABE 和△ACD 都为等边三角形，F 为BE 中点，DF 交于AC 于M ，连接DE .求证：（1）AM =MC ；（2）AB 平分DE .OC DB E F A BC ED A MD FE A13.如图，△ABC 为等边三角形，CF 为∠C 的外角平分线，在BC 上任取一点D ，使∠ADE =60°，DE 交CF 于点E .求证：△ADE 为等边三角形14.如图，在△ABC 中，AB =AC ，∠BAC =80°，O 为三角形内一点，∠OBC =10°，∠OCB =30°，求∠BAO 的度数.E F C D BA COBA。

新人教版八年级上册数学知识点梳理及巩固练习重难点突破课外机构补习优秀资料作轴对称图形知识讲解【学习目标】1．理解轴对称变换，能作出已知图形关于某条直线的对称图形．2．能利用轴对称变换，设计一些图案，解决简单的实际问题.3．运用所学的轴对称知识，认识和掌握在平面直角坐标系中，与已知点关于x轴或y轴对称点的坐标的规律，进而能在平面直角坐标系中作出与一个图形关于x轴或y轴对称的图形．4．能运用轴对称的性质，解决简单的数学问题或实际问题，提高分析问题和解决问题的能力．【要点梳理】要点一、对称轴的作法若两个图形成轴对称，其对称轴就是任何一对对应点所连线段的垂直平分线．因此只要找到一对对应点，再作出连接它们的线段的垂直平分线就可以得到这两个图形的对称轴．轴对称图形的对称轴作法相同．要点诠释：在轴对称图形和成轴对称的两个图形中，对应线段、对应角相等.成轴对称的两个图形，如果它们的对应线段或延长线相交，那么交点一定在对称轴上.如果两个图形的对应点连线被同一条直线垂直平分，那么这两个图形关于这条直线对称.【389300 作轴对称图形，用坐标表示轴对称】要点二、用坐标表示轴对称1.关于x轴对称的两个点的横（纵）坐标的关系已知P点坐标，则它关于x轴的对称点的坐标为，如下图所示：即关于x轴的对称的两点，坐标的关系是：横坐标相同，纵坐标互为相反数．2.关于y轴对称的两个点横（纵）坐标的关系已知P点坐标为，则它关于y轴对称点的坐标为，如上图所示．即关于y轴对称的两点坐标关系是：纵坐标相同，横坐标互为相反数．3.关于与x轴（y轴）平行的直线对称的两个点横（纵）坐标的关系P点坐标关于直线的对称点的坐标为．P点坐标关于直线的对称点的坐标为．【典型例题】类型一、作轴对称图形1、（2016•临夏州）如图，在平面直角坐标系中，△ABC的顶点A（0，1），B（3，2），C（1，4）均在正方形网格的格点上．（1）画出△ABC关于x轴的对称图形△A1B1C1；（2）将△A1B1C1沿x轴方向向左平移3个单位后得到△A2B2C2，写出顶点A2，B2，C2的坐标．【思路点拨】（1）直接利用关于x轴对称点的性质得出各对应点位置进而得出答案；（2）直接利用平移的性质得出各对应点位置进而得出答案．【答案与解析】解：（1）如图所示：△A1B1C1，即为所求；（2）如图所示：△A2B2C2，即为所求，点A2（﹣3，﹣1），B2（0，﹣2），C2（﹣2，﹣4）．【总结升华】此题主要考查了轴对称变换和平移变换，根据题意得出对应点位置是解题关键．举一反三：【变式】在下图中，画出△ABC关于直线MN的对称图形.A B C为所求.【答案】△'''类型二、轴对称变换的应用（将军饮马问题）【389300 作轴对称图形，例4】2、如图所示，如果将军从马棚M出发，先赶到河OA上的某一位置P，再马上赶到河OB上的某一位置Q，然后立即返回校场N．请为将军重新设计一条路线(即选择点P 和Q)，使得总路程MP＋PQ＋QN最短．【思路点拨】通过轴对称变换，将MP转化为M'P，QN转化为Q N'，要使总路程MP＋PQ＋QN最短，就是指M'P＋PQ＋Q N'最短，而这三条线段在一条直线上的时候最短.【答案与解析】见下图作点M关于OA的对称点M'，作点N关于OB的对称点N'，连接M N''交OA于P、交OB于Q，则M→P→Q→N为最短路线．【总结升华】本题主要是通过作对称点的方法得出结论，并利用了对称线段相等，三角形两边之和大于第三边的性质推得所作的图形符合条件，这是道综合性的应用问题.举一反三：【变式】（2014秋•花垣县期末）茅坪民族中学八（2）班举行文艺晚会，桌子摆成两直条（如图中的AO，BO），AO桌面上摆满了桔子，OB桌面上摆满了糖果，站在C处的学生小明先拿桔子再拿糖果，然后回到C处，请你在下图帮助他设计一条行走路线，使其所走的总路程最短？【答案】解：①分别作点C关于OA、OB的对称点是M、N，②连接MN，分别交OA于D，OB于E．则C→D→E→C为所求的行走路线．【389300 作轴对称图形，例4练习2】3、将军要检阅一队士兵，要求(如图所示)：队伍长为a，沿河OB排开(从点P到点Q)；将军从马棚M出发到达队头P，从P至Q检阅队伍后再赶到校场N．请问：在什么位置列队(即选择点P和Q)，可以使得将军走的总路程MP＋PQ＋QN最短?【答案与解析】见下图作法：作N 关于OB 的对称点N '，再作N N '''∥BO 且N N '''＝a (N ''在N '的左侧)；连接MN ''交OB 于点P ，再在OB 上取点Q 使得PQ ＝a (Q 在P 的右侧)，此时，MP ＋PQ ＋QN 最小．【总结升华】MP ＋PQ ＋QN 最小，其中PQ 是定值a ，问题转化为MP ＋QN 最小.因为将军要沿河走一段线段a ，如果能把这段a 提前走掉就可以转化为熟悉的问题了，于是考虑从'N 沿平行的方向走a 至''N ，连接''MN 即可.类型三、用坐标表示轴对称4、（2014秋•江津区期中）已知点A （2a ﹣b ，5+a ），B （2b ﹣1，﹣a+b ）．（1）若点A 、B 关于x 轴对称，求a 、b 的值；（2）若A 、B 关于y 轴对称，求﹙4a+b ﹚2014的值．【思路点拨】（1）根据关于x 轴对称点的坐标特点：横坐标不变，纵坐标互为相反数可得2a ﹣b=2b ﹣1，5+a ﹣a+b=0，解可得a 、b 的值；（2）根据关于y 轴对称点的坐标特点：横坐标互为相反数，纵坐标不变可得2a ﹣b+2b ﹣1=0，5+a=﹣a+b ，解出a 、b 的值，进而可得答案．【答案与解析】解：（1）∵点A 、B 关于x 轴对称，∴2a﹣b=2b ﹣1，5+a ﹣a+b=0，解得：a=﹣8，b=﹣5；（2）∵A、B 关于y 轴对称，∴2a﹣b+2b ﹣1=0，5+a=﹣a+b ，解得：a=﹣1，b=3，﹙4a+b ﹚2014=1．【总结升华】此题主要考查了关于x 、y 轴对称的点的坐标，关键是掌握点的坐标的变化规律．举一反三：【变式1】已知点A （2，3-）关于x 轴对称的点的坐标为点B （2m ，m n +），则m n -的值为（ ）．A ． 5-B ． 1-C ． 1D ． 5【答案】B ；提示：2m ＝2，m ＋n ＝3, 解得n ＝2, m ＝1，选B.【变式2】如图，ΔABC 中，点A 的坐标为（0，1），点C 的坐标为（4，3），点B 的坐标为（3，1），如果要使ΔABD 与ΔABC 全等，求点D 的坐标．【答案】共3个满足条件的点：1D （4，－1），2D （－1，3），3D （－1，－1）.。

初二数学期末考试轴对称知识点总结1轴对称图形和关于直线对称的两个图形2轴对称的性质轴对称图形的对称轴是任何一对对应点所连线段的垂直平分线;如两个图形关于某条直线对称，那么对称轴是任何一对对应点所连的线段的垂直平分线;线段垂直平分线上的点到线段两个端点的距离相等;到线段两个端点距离相等的点在这条线段的垂直平分线上。

3用坐标表示轴对称点（____，y）关于____轴对称的点的坐标是（____,-y），关于y 轴对称的点的坐标是（-____,y），关于原点对称的点的坐标是（-____,-y）.。

4等腰三角形等腰三角形的两个底角相等;（等边对等角）等腰三角形的顶角平分线、底边上的中线、底边上的高线互相重合;（三线合一）理解：已知等腰三角形的一线就可以推知另两线。

一个三角形的两个相等的角所对的边也相等。

（等角对等边）等腰三角形的判定：如果一个三角形有两个角相等，那么这两个角所对的边也相等。

（等角对等边）5等边三角形的性质和判定性质：等边三角形的三个内角都相等，都等于____度;判定：三个角都相等的三角形是等边三角形;有一个角是____度的等腰三角形是等边三角形;推论：1、直角三角形中，如果有一个锐角是____度，那么他所对的直角边等于斜边的一半。

2、在三角形中，大角对大边，大边对大角。

3、经过线段中点并且垂直于这条线段的直线，叫做这条线段的垂直平分线。

由一个平面图形得到它的轴对称图形叫做轴对称变换。

6轴对称图形____把一个图形沿着一条直线折叠，如果直线两旁的部分能够完全重合，那么这个图形就叫做轴对称图形。

这条直线就是它的对称轴。

这时我们也说这个图形关于这条直线（成轴）对称。

____把一个图形沿着某一条直线折叠，如果它能与另一个图形完全重合，那么就说这两个图关于这条直线对称。

这条直线叫做对称轴，折叠后重合的点是对应点,叫做对称点。

3、轴对称图形和轴对称的区别与联系4.轴对称与轴对称图形的性质①关于某直线对称的两个图形是全等形。

人教版初二上册数学第13章复习要点：轴对称
知识点对冤家们的学习十分重要，大家一定要仔细掌握，查字典数学网为大家整理了人教版初二上册数学第13章温习要点：轴对称，让我们一同窗习，一同提高吧!
经过线段中点并且垂直于这条线段的直线，叫做这条线段的垂直平分线(perpendicular bisector)。

轴对称图形的对称轴，是任何一对对应点所衔接线段的垂直平分线。

线段垂直平分线上的点与这条线段两个端点的距离相等。

由一个平面图形失掉它的轴对称图形叫做轴对称变换。

等腰三角形的性质：
等腰三角形的两个底角相等。

(等边对等角)
等腰三角形的顶角平分线、底边上的中线、底边上的高相互重合。

(三线合一)(附：顶角+2底角=180°)
假设一个三角形有两个角相等，那么这两个角所对的边也相等。

(等角对等边)
有一个角是60°的等腰三角形是等边三角形。

在直角三角形中，假设一个锐角等于30°，那么它所对的直角边等于斜边的一半。

只需这样踏踏实实完成每天的方案和小目的，就可以自若地
应对新学习，到达久远目的。

由查字典数学网为您提供的人教版初二上册数学第13章温习要点：轴对称，祝您学习愉快!。