昆工08数学分析考研

昆明理工大学2008年硕士研究生招生入学考试试题(A 卷)考试科目代码：822 考试科目名称 ： 水力学 试题适用招生专业 ：水文学及水资源、水力学及河流动力学、水利水电工程、农业水土工程考生答题须知1． 所有题目（包括填空、选择、图表等类型题目）答题答案必须做在考点发给的答题纸上，做在本试题册上无效。

请考生务必在答题纸上写清题号。

2． 评卷时不评阅本试题册，答题如有做在本试题册上而影响成绩的，后果由考生自己负责。

3． 答题时一律使用蓝、黑色墨水笔或圆珠笔作答（画图可用铅笔），用其它笔答题不给分。

4． 答题时不准使用涂改液等具有明显标记的涂改用品。

一、是非题（每小题2分，共30分。

正确的打√，错误的打×）1．在相同的边界条件下，层流过水断面上的流速分布比紊流过水断面上的流速分布均匀。

2．根据达西公式gv R l h f 242λ=，层流沿程水头损失与流速平方成正比。

3．棱柱体明渠恒定渐变流的水面曲线有12条，而地下河槽无压渗流的浸润曲线只有6条。

4．液体的粘滞性随液体温度的升高而减小。

5．体积弹性系数K 越大的液体，越容易被压缩。

6．在平衡液体中等压面不是等势面，但等压面与质量力正交。

7．运动流体过水断面上的动水压强分布规律必定与静水压强分布规律不同。

8．急流时断面比能随水深的增大而减小。

9．棱柱体水平明渠中产生一水跃，若在水跃段的底板上加一低坎，则其它条件不变时，跃后水深将减小。

10．当WES 堰的下游水位超过堰顶时，就是淹没出流。

11．其他条件相同时，增加管道的壁厚，可减小水击波在有压管道中的传播速度。

12. 恒定流时一定没有时变加速度和位变加速度。

13. 平面势流的流函数是调和函数。

14．φ与ψ为平面势流的流速势函数和流函数，则yx ∂∂=∂∂ψφ。

15．重力相似准则是指原型水流与模型水流的雷诺数相等。

二、选择题（每题2分，共16分）1．梯形断面明渠水力最佳断面的水力半径R 与水深h 的关系为a. R=hb. R=0.5hc. h=0.5Rd. R=1.5h2．平底棱柱形明渠发生水跃，h 1、h 2分别为跃前水深和跃后水深，其水跃函数 J (h 1)与 J (h 2)的关系是a. J(h1)= J(h2)b. J(h1)>J(h2)c. J(h1)< J(h2)d. J(h1)≠J(h2)3．紊流中粘滞底层厚度δ比绝对粗糙高度∆大得多的壁面称为a. 水力光滑面b. 过渡粗糙面c. 水力粗糙面d. 以上答案均不对4．溢流坝下泄水流收缩断面水深h c的跃后水深为h2，h t为下游水深。

昆明理工大学数学分析历年考研真题集(2016～2020)本真题集由考途学者倾情汇编，仅供研友学习！真题集内容:2020年昆明理工大学数学分析考研真题2018年昆明理工大学数学分析考研真题2017年昆明理工大学数学分析考研真题2016年昆明理工大学数学分析考研真题2020年昆明理工大学数学分析考研真题考生答题须知1．所有题目（包括填空、选择、图表等类型题目）答题答案必须做在考点发给的答题纸上，做在本试题册上无效。

请考生务必在答题纸上写清题号。

2．评卷时不评阅本试题册，答题如有做在本试题册上而影响成绩的，后果由考生自己负责。

3．答题时一律使用蓝、黑色墨水笔或圆珠笔作答（画图可用铅笔），用其它笔答题不给分。

4．答题时不准使用涂改液等具有明显标记的涂改用品。

1、（15分）设为非空有上界的数集.证明：当且仅当，其中和分别表示的上确界和最大值.2、（15分）求下列极限3、（15分）已知函数在点处连续，计算和.4、（15分）证明函数在点处可微当且仅当函数在点处可导.5、（15分）利用微分中值定理证明：，其中.6、（15分）求幂级数的收敛域与和函数.7、（15分）求曲线在点处的切线方程.8、（15分）证明在点连续且偏导数存在，但在此点不可微.9、（15分）计算曲线积分，其中是由和所围成的闭曲线.10、（15分）设某流体的流速为（为常数），求单位时间内从球面的内部流过球面的流量.2018年昆明理工大学数学分析考研真题一、计算及判断（每小题5分，共20分）1、设函数arctan ()x y f e =，求微分dy ；2、求极限1321lim 242n n n→∞-⋅⋅⋅ ；3、设函数1,77(),711(1)sin ,11x x f x x x x x x ⎧-∞<<-⎪+⎪=-≤≤⎨⎪⎪-<<+∞-⎩，指出其间断点及类型，并说明理由；4、求函数()arctan f x x =在0x =的左、右导数．二、证明下列各题（每小题5分，共20分）1、用X ε-定义证明lim sin0x xπ→+∞=；2、叙述函数极限0lim ()x f x +→存在的归结原则；3、运用归结原则证明01lim cos x x+→不存在；4、应用拉格朗日中值定理不等式：aab a b b a b -<<-ln ，其中b a <<0．三、（10分）证明：若函数f 在R 连续，且()()xaf x f t dt =⎰，则()0f x ≡．四、（10分）证明：若数列{}n na 收敛，且级数11()n n n n a a ∞-=-∑收敛，则级数1nn a ∞=∑收敛．五、计算或证明下列各题（每小题5分，共35分）1、求极限221lim nn i n n i →∞=+∑；2、求导数32x x d dx ⎰；3、证明瑕积分130arctan 1x dx x -⎰发散;4、求极限00lim πα→⎰；5、求函数()2xf x π-=在(0,2)π上的傅里叶展开式；6、计算第一型曲线积分Lyds ⎰，其中L 为单位上半圆周221x y +=；7、计算第一型曲面积分SzdS ⎰⎰，其中S 为平面1=++z y x 在第一卦限中的部分.六、（10分）证明函数1,()1x f x x ⎧=⎨-⎩为有理数，，为无理数在]1,0[上有界但不可积．七、（10分）求函数⎪⎩⎪⎨⎧=+≠++-=0,00 ,),(22222233y x y x y x y x y x f 在原点的偏导数)0,0(x f 与)0,0(y f ,并证明),(y x f 在点)0,0(是不可微的．八、（10分）利用适当的坐标变换计算二重积分{}()sin(),(,)0,0Dx y x y dxdy D x y x y x y ππ+-=≤+≤≤-≤⎰⎰．九、（10分）设f 是一元函数,试问应对f 提出什么条件,方程)()()(2y f x f xy f +=在点)1,1(的邻域内就能确定出唯一的y 为x 的函数?十、（10分）用高斯公式计算第二型曲面积分22()Syzdydz x z ydzdx xydxdy +++⎰⎰，其中22:4()S y x z =-+，在0x z 面右侧部分内侧.十一、（5分）请举例说明：在有理数集内，单调有界定理一般都不成立.2017年昆明理工大学数学分析考研真题一、计算下列各题（每小题6分，共30分）1、设函数sin ()x y f e =，求微分dy ；2、求极限22011lim()sin x x x→-；3、求函数()arctan f x x =在0x =的左、右导数；4、指出函数||sin )(x xx f =的间断点，并说明其类型;5、求不定积分二、证明下列各题（每小题7分，共28分）1、用N ε-定义证明0n →∞-=；2、应用柯西收敛准则，证明数列2sin1sin 2sin 222n n na =+++ 收敛；3、设f 是定义在R 上的函数，且对任何12,x x R ∈，都有1212()()()f x x f x f x +=⋅，若(0)1f '=，证明：对任何x R ∈，有()()f x f x '=；4、应用凹凸性证明不等式：()lnln ln ,,02x yx y x x y y x y ++≤+>.三、计算下列各题：（5分×3=15分）1、求无穷积分2x xe dx +∞-⎰的值；2、将函数1()1f x x =+展成1x -的幂级数；3、求函数22222(,)()x y f x y x y x y =+-在点(0,0)的重极限和累次极限.四、（10分）证明狄利克雷函数⎩⎨⎧=为无理数，为有理数，x x x D 0,1)(在]1,0[上有界但不可积.五、计算或证明下列各题：（6分×5=30分）1、设f 为连续可微函数，求()()xad x t f t dt dx '-⎰；2、求函数u xyz =在点(5,1,2)A 的梯度以及沿着从该点到点(9,4,14)B 的方向AB上的方向导数；3、、计算第二型曲线积分Lydx ⎰，其中L 为)0(sin π≤≤=x x y 与x 轴所围的闭曲线，依顺时针方向；4、0sin x e xdx α+∞-⎰在00[,](0)a a +∞>上一致收敛；5、221SdS x y+⎰⎰，其中S 是柱面222x y R +=被平面0,z z H ==所截取的部分；六、（10分）证明：函数2222222,0(,)0,0x yx y x y f x y x y ⎧+≠⎪+=⎨⎪+=⎩在(0,0)点连续且偏导数存在，但不可微.七、（10分）求表面积一定而体积最大的长方体.八、（10分）用高斯公式计算曲面积分22()Syzdydz x z ydzdx xydxdy +++⎰⎰，其中22:4()S y x z =-+，在xoz 面右侧部分外侧.九、（7分）用定义证明1()f x x=在(0,1)内不一致连续.2016年昆明理工大学数学分析考研真题一、（20分）求下列极限（每小题4分，共20分）(1)sin(!)lim;1n n n →∞+(2)lim ;n →∞⎛⎫⋅⋅⋅+(3)22001limsin();tan x e x t dt x →⎰(4)x (5)0ln(1arcsin )limarcsin x x x→+二、（20分）求下列导数或微分（每小题5分，共20分）(1)设25(5)(4)(4),(2)(4)x x y x x x +-=>++求;dy dx (2)已知(),x f x x =求();df x (3)设(sin ),(1cos ),x a t t y a t =-⎧⎨=-⎩求2.t dydx π=(4)设(,),x yu f y z=且f 具有连续的偏导数，求.du 三、（8分）求下列积分（每小题4分，共8分）(1)1;⎰(2)21.1dx x +∞-∞+⎰四、（40分）按要求计算下列曲线积分、曲面积分和重积分（每小题8分，共40分）(1)计算第一型曲线积分(),Lx y ds +⎰其中L 是以(0,0),(1,0),(0,1)O A B 为顶点的三角形.(2)利用格林公式计算第二型曲线积分(sin )(cos 1),x x ABe y y dx e y dy -+-⎰其中AB 为由(,0)a 到(0,0)经过圆22x y ax +=上半部分的路线.(3)用变量变换求二重积分,x y x yDedxdy -+⎰⎰其中D 是由1,0,0=+==y x y x 所围成的区域.(4)计算第一型曲面积分,SxyzdS ⎰⎰其中S 为平面1=++z y x 在第一卦限中的部分.(5)利用高斯公式计算第二型曲面积分222Sx dydz y dzdx z dxdy++⎰⎰Ò其中S 是锥面222z y x =+与平面h z =所围空间区域)0(h z ≤≤的表面，方向取外侧.五、（10分）按要求完成下列各题（每小题5分，共10分）(1)设1,()0,x D x x ⎧=⎨⎩为有理数为无理数,.证明函数项级数31()n D x n∞=∑在),(+∞-∞上一致收敛；(2)用间接方法求非初等函数20()xt F x e dt -=⎰在0=x 处的幂级数展开式.六、（10分）求2()f x x x =+在x ππ-<<上的傅里叶级数，并应用它推出2211.6n n π∞==∑七、（8分）叙述函数()f x 在区间I 上无界的定义，并应用它证明31()f x x=在区间(0,1)上无界.八、（8分）用定义证明22lim(610) 2.x x x →-+=九、（9分）按柯西准则叙述极限lim n n a →∞存在的充要条件，并应用它证明222111lim(1)23n n →∞+++⋅⋅⋅+存在.十、（9分）设函数()f x 在[0,1]上连续，在(0,1)内二阶可导，证明存在(0,1),ξ∈使得11(1)2((0)().24f f f f ξ''-+=十一、（8分）证明函数z =在点(0,0)连续但偏导数不存在.。

昆明理工大学2007年硕士研究生招生入学考试试题(A 卷)考试科目代码：805 考试科目名称 ： 数字电路试题适用招生专业 ： 物理电子学考生答题须知1、所有题目（包括填空、选择、图表等类型题目）答题答案必须做在考点发给的答题纸上，做在本试题册上无效。

请考生务必在答题纸上写清题号。

2、评卷时不评阅本试题册，答题如有做在本试题册上而影响成绩的，后果由考生自己负责。

3、答题时一律使用蓝、黑色墨水笔或圆珠笔作答（画图可用铅笔），用其它笔答题不给分。

1、答题时不准使用涂改液等具有明显标记的涂改用品。

昆明理工大学2007年硕士研究生招生入学考试试题图2 -1(1)当三极管T 饱和导通时，输入端A 、B 对地的电压在什么范围？(3)如果将输入端A 、B 同时与E C (4)在正逻辑约定下，该电路具有什么(5)在负逻辑约定下，该电路具有什么逻辑功能？昆明理工大学2007年硕士研究生招生入学考试试题图4 -1 图4 -2 图4 -3(1)对图4-1电路，在图4- 4中给出了J、K、CP的波形，请图4 -4试题适用招生专业 ：物理电子学考生答题须知4、所有题目（包括填空、选择、图表等类型题目）答题答案必须做在考点发给的答题纸上，做在本试题册上无效。

请考生务必在答题纸上写清题号。

5、评卷时不评阅本试题册，答题如有做在本试题册上而影响成绩的，后果由考生自己负责。

6、答题时一律使用蓝、黑色墨水笔或圆珠笔作答（画图可用铅笔），用其它笔答题不给分。

7、答题时不准使用涂改液等具有明显标记的涂改用品。

一、逻辑代数（26分）1、（16分）对图1所示逻辑图：图1(1)写出与图1对应的逻辑代数表达式；(2)将逻辑代数表达式改写成最小项和式（标准与或式）；(3)从最小项和式作出卡诺图；(4)从卡诺图化简逻辑函数，写出最简与或表达式；(5)根据最简与或表达式画出逻辑图。

2、（10分）设有二输入逻辑门和，构成下面组合逻辑函数：()B A F ,1()B A F ,2()()()()()()()()⎩⎨⎧==i i o i i C Y X F F Y X F F C Y X C C Y X F F C Y X S ,,,,,,,,,,122211如果该逻辑函数为全加器，分别写出和的逻辑表达式。

昆明理工大学2008年秋季入学博士研究生招生入学考试试题
考试科目代码：2158 考试科目名称：运筹学
试题适用招生专业：管理科学与工程、决策科学与决策支持系统、科教管理与知识创新、
系统工程、项目管理与持续创新发展、信息管理与信息系统
考生答题须知
1．所有题目（包括填空、选择、图表等类型题目）答题答案必须做在考点发给的答题纸上，做在本试题册上无效。

请考生务必在答题纸上写清题号。

2．评卷时不评阅本试题册，答题如有做在本试题册上而影响成绩的，后果由考生自己负责。

3．答题时一律使用蓝、黑色墨水笔或圆珠笔作答（画图可用铅笔），用其它笔答题不给分。

4．答题时不准使用涂改液等具有明显标记的涂改用品。

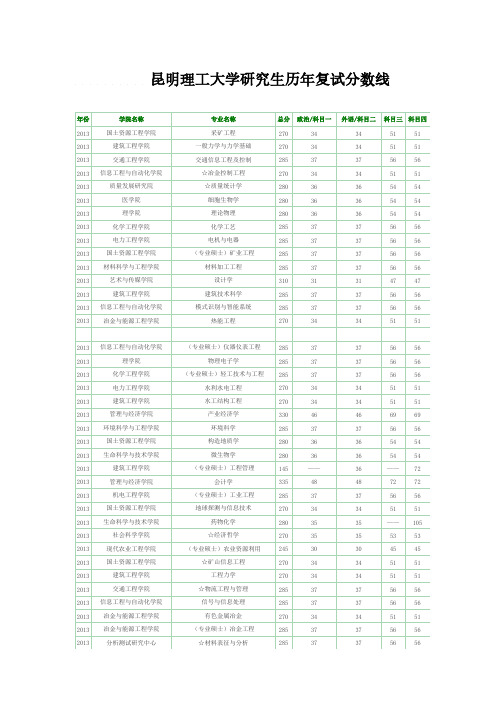
昆明理工大学研究生历年复试分数线年份学院名称专业名称总分政治/科目一外语/科目二科目三科目四2013国土资源工程学院采矿工程27034345151 2013建筑工程学院一般力学与力学基础27034345151 2013交通工程学院交通信息工程及控制28537375656 2013信息工程与自动化学院☆冶金控制工程27034345151 2013质量发展研究院☆质量统计学28036365454 2013医学院细胞生物学28036365454 2013理学院理论物理28036365454 2013化学工程学院化学工艺28537375656 2013电力工程学院电机与电器28537375656 2013国土资源工程学院（专业硕士）矿业工程28537375656 2013材料科学与工程学院材料加工工程28537375656 2013艺术与传媒学院设计学31031314747 2013建筑工程学院建筑技术科学28537375656 2013信息工程与自动化学院模式识别与智能系统28537375656 2013冶金与能源工程学院热能工程270343451512013信息工程与自动化学院（专业硕士）仪器仪表工程28537375656 2013理学院物理电子学28537375656 2013化学工程学院（专业硕士）轻工技术与工程28537375656 2013电力工程学院水利水电工程27034345151 2013建筑工程学院水工结构工程27034345151 2013管理与经济学院产业经济学33046466969 2013环境科学与工程学院环境科学28537375656 2013国土资源工程学院构造地质学28036365454 2013生命科学与技术学院微生物学28036365454 2013建筑工程学院（专业硕士）工程管理145——36——72 2013管理与经济学院会计学33548487272 2013机电工程学院（专业硕士）工业工程28537375656 2013国土资源工程学院地球探测与信息技术27034345151 2013生命科学与技术学院药物化学2803535——105 2013社会科学学院☆经济哲学27035355353 2013现代农业工程学院（专业硕士）农业资源利用24530304545 2013国土资源工程学院☆矿山信息工程27034345151 2013建筑工程学院工程力学27034345151 2013交通工程学院☆物流工程与管理28537375656 2013信息工程与自动化学院信号与信息处理28537375656 2013冶金与能源工程学院有色金属冶金27034345151 2013冶金与能源工程学院（专业硕士）冶金工程28537375656 2013分析测试研究中心☆材料表征与分析285373756562013理学院☆应用化学物理28036365454 2013化学工程学院制浆造纸工程28537375656 2013电力工程学院电力电子与电力传动285373756562013国土资源工程学院土地资源管理33548487272 2013艺术与传媒学院（专业硕士）艺术设计31031314747 2013建筑工程学院市政工程28537375656 2013管理与经济学院国民经济学33046466969 2013信息工程与自动化学院计算机软件与理论28537375656 2013信息工程与自动化学院（专业硕士）计算机技术28537375656 2013国土资源工程学院地图学与地理信息系统28036365454 2013电力工程学院农业水土工程27034345151 2013建筑工程学院风景园林学28537375656 2013管理与经济学院数量经济学33046466969 2013环境科学与工程学院☆再生资源科学与技术28537375656 2013管理与经济学院技术经济及管理33548487272 2013机电工程学院机械电子工程28537375656 2013国土资源工程学院大地测量学与测量工程28537375656 2013生命科学与技术学院生物物理学28036365454 2013法学院民商法学30539395959 2013社会科学学院外国哲学27035355353 2013现代农业工程学院农业水土工程27034345151 2013国土资源工程学院☆矿产资源经济27034345151 2013交通工程学院动力机械及工程27034345151 2013信息工程与自动化学院测试计量技术及仪器28537375656 2013质量发展研究院☆质量法学30539395959 2013现代农业工程学院（专业硕士）设施农业24530304545 2013医学院遗传学28036365454 2013理学院应用数学28036365454 2013化学工程学院化学工程28537375656 2013国土资源工程学院（专业硕士）地质工程28537375656 2013材料科学与工程学院材料学28537375656 2013艺术与传媒学院艺术学理论31031314747 2013建筑工程学院建筑设计及其理论28537375656 2013信息工程与自动化学院系统工程28537375656 2013冶金与能源工程学院工程热物理27034345151 2013理学院☆动力系统及其计算27034345151 2013化学工程学院（专业硕士）化学工程28537375656 2013电力工程学院水力学及河流动力学27034345151 2013建筑工程学院桥梁与隧道工程28537375656 2013管理与经济学院金融学33046466969 2013环境科学与工程学院生态学28036365454 2013信息工程与自动化学院软件工程285373756562013国土资源工程学院古生物学与地层学28036365454 2013生命科学与技术学院生理学28036365454 2013建筑工程学院技术经济及管理33548487272 2013管理与经济学院管理科学与工程33548487272 2013机电工程学院（专业硕士）机械工程28537375656 2013国土资源工程学院矿产普查与勘探27034345151 2013生命科学与技术学院（专业硕士）生物工程28537375656 2013法学院国际法学30539395959 2013社会科学学院科学技术哲学27035355353 2013现代农业工程学院（专业硕士）农业工程285373756562007年：哲学　[01] ：　总分 295 分，　单科 41 （ 62 ）；经济学 [02] ：　总分 315 分，　单科 48 （ 72 ）；法学　[03] ：　总分 325 分，　单科 48 （ 72 ）；艺术学 [0504] ：总分 315 分，　单科 40 （ 60 ）；理学　[07] ：　总分 295 分，　单科 44 （ 66 ）；工学（不含照顾专业）：总分 280 分，单科 36 （ 54 ）；工学照顾专业（一级学科）（包括力学、冶金工程、动力工程及工程热物理、水利工程、地质资源与地质工程、矿业工程、 农业工程）：总分 270 分，单科 33 （ 50 ）；医学 [10] ：　总分 285 分，单科 39 （ 117 ）；管理学 [12] （不含 MBA 专业）：总分 320 分，单科 49 （ 74 ）；工商管理硕士 [MBA][120280] ：总分 145 分，单科 38 （ 76 ）；（注：单科成绩中括号内数字为满分大于 100 分科目成绩，括号外数字为满分 100 分科目成绩）2008年：哲学[01] ：总分280 分，单科35 （53 ）；经济学[02] ：总分320 分，单科48 （72 ）；法学[03] ：总分315 分，单科47 （71 ）；艺术学[0504] ：总分305 分，单科39 （59 ）；理学[07] ：总分285 分，单科41 （62 ）；工学（不含照顾专业）：总分285 分，单科38 （57 ）；工学照顾专业（一级学科）（包括力学、冶金工程、动力工程及工程热物理、水利工程、地质资源与地质工程、矿业工程、农业工程）：总分270 分，单科33 （50 ）；医学[10] ：总分280 分，单科38 （114 ）；管理学[12] （不含MBA 专业）：总分315 分，单科48 （72 ）；工商管理硕士[MBA][120280] ：总分155 分，单科44 （88 ）；（注：单科成绩中括号内数字为满分大于100 分科目成绩，括号外数字为满分100 分科目成绩）2009年：　哲学[01]：总分260分，单科31（47）； 经济学[02]：总分295分，单科41（62）； 法学[03]：总分295分，单科40（60）； 艺术学[0504]：总分300分，单科36（54）； 理学[07]：总分260分，单科32（48）； 工学（不含照顾专业）：总分255分，单科31（47）； 工学照顾专业（一级学科）（包括力学、冶金工程、动力工程及工程热物理、水利工程、地质资源与地质工程、矿业工程、农业工程）：总分240分，单科31（47）； 医学[10]：总分265分，单科33（99）； 管理学[12]（不含MBA专业）：总分295分，单科41（62）； 工商管理硕士[MBA]：总分135分，单科40（68）； （注：单科成绩中括号内数字为满分大于100分科目成绩，括号外数字为满分100分科目成绩）2010年：哲学[01]：总分250分，单科30（45）；经济学[02]：总分310分，单科40（60）；法学[03]：总分290分，单科37（56）；艺术学[0504]：总分285分，单科30（45）；理学[07]：总分260分，单科31（47）；工学[08]（不含照顾专业）：总分255分，单科30（45）；工学照顾专业（一级学科）（包括力学、冶金工程、动力工程及工程热物理、水利工程、地质资源与地质工程、矿业工程、农业工程）：总分240分，单科30（45）；医学[10]：总分260分，单科31（93）；管理学[12]（不含MBA专业）：总分310分，单科40（60）；工商管理硕士[4601，MBA]：总分145分，单科37（74）；建筑学硕士[4401]: 总分255分，单科30（45）；艺术硕士[5501]: 总分285分，单科30（45）；工程硕士[4301]（不含照顾专业）: 总分255分，单科30（45）；工程硕士照顾专业（包括冶金工程、动力工程、水利工程、地质工程、矿业工程、安全工程、农业工程）: 总分240分，单科30（45）；（注：单科成绩中括号内数字为满分大于100分科目成绩，括号外数字为满分100分科目成绩）2011年：哲学：总分275分，单科35（53）；经济学：总分330分，单科50（75）；法学：总分305分，单科40（60）；艺术学：总分300分，单科30（45）；理学：总分275分，单科35（53）；工学（不含照顾专业）：总分280分，单科35（53）；工学照顾专业（一级学科）（包括力学、冶金工程、动力工程及工程热物理、水利工程、地质资源与地质工程、矿业工程、农业工程）：总分260分，单科35（53）；医学（不含中医学）：总分280分，单科35（105）；管理学：总分330分，单科50（75）；工商管理硕士、工程管理硕士：总分145分，单科35（70）；建筑学硕士、工程硕士: 总分280分，单科35（53）；工程硕士照顾专业（包括冶金工程、动力工程、水利工程、地质工程、矿业工程、安全工程、农业工程）: 总分260分，单科35（53）；艺术硕士: 总分300分，单科30（45）；农业推广硕士：总分240分，单科30（45）。

《昆明理工大学2015年硕士研究生招生考试命题科目表》学院科目代码科目名称
611 地图学
612 矿物岩石学
613 地籍测量学
801 GIS原理及应用
802 地质学基础
803 测量平差
国土资源工程学院
804 遥感概论
805 金属矿床地下开采
806 矿物加工工程学（综合）
807 安全系统工程
808 土地管理学总论
809 冶金物理化学
冶金与能源工程学院
810 工程流体力学
811 机械原理
812 电工电子学
813 运筹学
机电工程学院
814 包装材料学
828 印刷色彩学
815 电子技术（含模拟、数字部分）
816 自动控制原理
信息工程与自动化学院
817 信号与系统
818 计算机学科专业基础综合
820 电力系统分析
电力工程学院
821 水力学（电力院）
822 汽车理论
823 内燃机原理
交通工程学院
824 交通工程学
825 汽车运用工程
826 物流工程学
614 环境生态学
827 环境学概论
环境科学与工程学院
829 固体废物处理与处置
830 环境工程学
化学工程学院831 化学反应工程
615 教育经济学
836 西方经济学
管理与经济学院
837 管理学
838 供应链与物流管理
土木工程学院835 建筑施工管理。

2018年云南昆明理工大学数学分析考研真题A 卷一、计算及判断（每小题5分，共20分）1、设函数arctan ()x y f e=，求微分dy ； 2、求极限1321lim 242n n n→∞-⋅⋅⋅； 3、设函数1,77(),711(1)sin ,11x x f x x x x x x ⎧-∞<<-⎪+⎪=-≤≤⎨⎪⎪-<<+∞-⎩，指出其间断点及类型，并说明理由； 4、求函数()arctan f x x =在0x =的左、右导数．二、证明下列各题（每小题5分，共20分）1、用X ε-定义证明lim sin 0x x π→+∞=；2、叙述函数极限0lim ()x f x +→存在的归结原则； 3、运用归结原则证明01lim cos x x+→不存在；4、应用拉格朗日中值定理不等式：a a b a b b a b -<<-ln ，其中b a <<0． 三、（10分）证明：若函数f 在R 连续，且()()xa f x f t dt =⎰，则()0f x ≡． 四、（10分）证明：若数列{}n na 收敛，且级数11()n n n n aa ∞-=-∑收敛，则级数1n n a ∞=∑收敛． 五、计算或证明下列各题（每小题5分，共35分）1、求极限 221lim nn i n n i→∞=+∑； 2、求导数 32x x d dx ⎰； 3、证明瑕积分130arctan1x dx x-⎰发散; 4、求极限 00lim πα→⎰； 5、求函数()2x f x π-=在(0,2)π上的傅里叶展开式； 6、计算第一型曲线积分L yds ⎰，其中L 为单位上半圆周221x y +=； 7、计算第一型曲面积分SzdS ⎰⎰，其中S 为平面1=++z y x 在第一卦限中的部分.六、（10分）证明函数1,()1x f x x ⎧=⎨-⎩为有理数，，为无理数在]1,0[上有界但不可积． 七、（10分）求函数⎪⎩⎪⎨⎧=+≠++-=0,00 ,),(22222233y x y x y x y x y x f 在原点的偏导数)0,0(x f 与)0,0(y f , 并证明),(y x f 在点)0,0(是不可微的．八、（10分）利用适当的坐标变换计算二重积分{}()sin(),(,)0,0Dx y x y dxdy D x y x y x y ππ+-=≤+≤≤-≤⎰⎰．九、（10分）设f 是一元函数,试问应对f 提出什么条件,方程)()()(2y f x f xy f +=在点)1,1(的邻域内就能确定出唯一的y 为x 的函数?十、（10分）用高斯公式计算第二型曲面积分22()S yzdydz x z ydzdx xydxdy +++⎰⎰，其中22:4()S y x z =-+，在0x z 面右侧部分内侧.十一、（5分）请举例说明：在有理数集内，单调有界定理一般都不成立.。