王新敞
奎屯 新疆
七、二次函数与方程、不等式的关系
判别式 △=b2-4ac 二次函数 y=ax2+bx+c (a>0)的图象 一元二次方程 ax2+bx+c=0 (a>0) 的根 △>0 y
x1 o x2
△=0 y x
△<0 y
o x1=x2
x
o
x
有两相异实根 x1, x2 (x1<x2)
有两相等实根 b x1=x2= - 2 a b {x | x≠- 2a }
o
y o
2 4
x
x
2 4
(3) 若 a > 4 时,f ( x ) 在[ 2,4 ]上为减函数 ∴ f ( x ) min = f ( 4 ) = 18 -8a
y
2 4
故f ( x )min
a2 6 4a 2 a2 2 a 4 18 8a a 4
王新敞
综上所述, a=1- 2 或 a=5+ 10.
一、二次函数的解析式
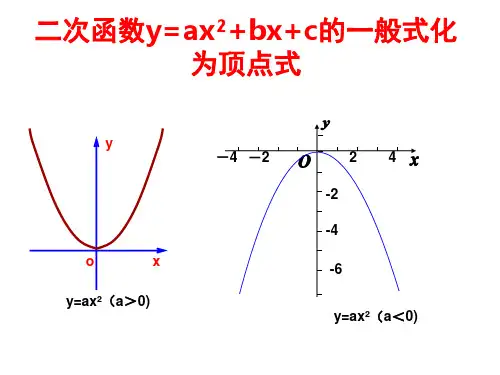
1.一般式: y=ax2+bx+c(a≠0); 2.顶点式: y=a(x -m)2+n(其中(m, n)为抛物线的顶点坐标); 3.两根式: y=a(x -x1)(x -x2)(其中x1, x2为抛物线与 x 轴两交点 的横坐标);
二、二次函数的图象
有关知识: 图象形状; 对称轴; 顶点坐标; 与 x 轴交点坐标; 截 x 轴线段长.
-----------“活动范围” 定义域(区间)
引例. 已知a,b,c∈R,函数f(x)=ax2+bx+c, 若f(0)= f(4)> f(1), 则 A. a>0, 4a+b=0 C. a>0, 2a+b=0 B. a<0, 4a+b=0 D. a<0, 2a+b=0