二次函数的对称轴(学练结合)

二次方程对称轴公式二次函数是数学中一个重要的函数，其图像是一个平滑且连续的曲线。

在二次函数中，对称轴是一个非常重要的概念，它具有很多重要的性质和应用。

本文将详细介绍二次函数的对称轴概念、性质以及一些相关的应用。

一、对称轴的概念在二次函数中，对称轴是指二次函数图像上所有点关于条直线对称。

具体来说，二次函数的对称轴是一个与y轴平行的直线，它将二次函数图像分成两个完全相同的部分。

这条直线通常被表示为x=a，其中a是一个实数。

对称轴也可以称为对称线或轴线。

二、对称轴的计算方法对称轴的计算方法可以通过函数的标准型或一般型来求解。

标准型二次函数的形式为f(x)=ax^2+bx+c，其中a、b、c是实数且a不等于0。

对称轴的x坐标可以通过-b/2a来计算，因为对称轴与y轴平行，所以对称轴的方程可以表示为x=-b/2a。

举例说明：假设给定一个二次函数f(x)=2x^2+3x-1，我们可以先通过计算得到a=2，b=3，c=-1、然后通过-b/2a来计算对称轴的x坐标，即(-3)/(2*2)=-3/4、所以这个二次函数的对称轴的方程为x=-3/4三、对称轴的性质对称轴具有以下性质：1.对称轴与二次函数图像的交点称为顶点，顶点是二次函数图像的最高点或最低点。

2.顶点在对称轴上的投影称为顶点的坐标。

四、对称轴的几何意义对称轴具有几何意义，它能够帮助我们推测二次函数的图像。

具体来说，对称轴的倾斜方向和位置可以告诉我们一些关于二次函数图像的重要信息。

1.如果对称轴是水平的，那么二次函数图像开口朝上或朝下。

2.如果对称轴是垂直的，那么二次函数图像开口向左或向右。

3.对称轴的位置可以告诉我们函数图像是向上移动还是向下移动。

五、对称轴的应用对称轴在数学问题以及实际应用中有许多重要的应用，例如：1.解方程：通过对称轴公式，我们可以很容易地求解二次方程的解。

对称轴公式是通过找到二次函数图像与x轴交点来得到二次方程的解的。

2.复杂问题的化简：在解决一些复杂问题时，对称轴可以帮助我们简化问题，从而更容易地解决问题。

巧用二次函数对称性解题
解题用二次函数的对称性，是一种非常有效的方法，也是数学中最常见的一类数学解题方法，它具有广泛的应用。

本文就来讨论二次函数的对称性在数学解题中的运用。

二次函数的对称性指的是，对某函数的函数值又特定的轴线上的特征而言，存在一条对称轴，使得当我们沿着该对称轴旋转时，所有的点不变。

一般来说，二次函数的对称性都是以一条直线或者129°角线作为对称轴。

因此，用二次
函数的对称性解题时，只需要找出函数在哪一条轴上存在对称效应即可。

例1：y＝2x2-4x+1。

此二次函数的对称轴是一条y轴中的x=1线，因为该函数在y轴上的x=1时存在对称效果，其图像的左侧和右侧的图像是相同的。

例2：y＝x2-3x+2。

此二次函数的对称轴是一条129°角线，因为该函数在y轴上的x=1时存在对称效果，其
图像的左侧和右侧的图像是相同的。

二次函数的对称性在很多数学考试题中都有着非常重要的地位，而且它在考试题解答中也
是最基本也是最有效的方法之一。

如果考生能够熟练掌握这种方法，就可以有效地提升自
己的解题能力。

在使用二次函数的对称性来解决数学解题时，考生需要注意的是，对函数的特征有充分的
理解，以及在存在两个或以上的函数的情况下，解题的思路清晰明确，并且要尽可能用函
数的方法来解决。

总之，二次函数的对称性实际上是一种很有用的解题方法，在解决很多数学解题问题时，
可以发挥它独特的数学优势。

正确运用二次函数的对称性，可以使考生有效地提升解题能力，为自己取得良好的成绩贡献自己的一份力量。

二次函数中像的对称轴性质和性质二次函数是高中数学中的一个重要知识点，它是一种含有二次项的多项式函数。

在二次函数中，对称轴性质是一个关键的特性，它可以帮助我们更好地理解函数的图像和性质。

本文将通过详细探讨二次函数中对称轴性质和其他相关性质，来增加我们对二次函数的理解和运用。

一、对称轴的定义和性质对称轴是二次函数的一个重要特性，它可以帮助我们判断函数的图像在坐标平面上的对称性。

对称轴是指二次函数的图像关于某一直线对称。

具体而言，对称轴是通过二次函数的顶点的垂直线。

使用数学符号表示对称轴为x=a，其中a是实数。

二次函数的对称轴的性质如下：1. 对称性：如果一个点(x, y)在函数的图像上，则与该点关于对称轴对称的点(-x, y)也在图像上。

2. 相对位置：对称轴将二次函数图像分成两个完全对称的部分，分别位于对称轴两侧。

3. 对称轴上的点：对称轴上的所有点，其函数值 (y 坐标) 相等，因为它们关于对称轴对称。

4. 对称轴和顶点的关系：二次函数的对称轴必定通过其顶点，也就是对称轴的x坐标等于顶点的x坐标。

二、对称轴的寻找方法1. 根据函数的表达式：对于形如y=ax^2+bx+c的二次函数，对称轴的x坐标为-x/b。

2. 根据顶点坐标：对于形如y=a(x-h)^2+k的二次函数，对称轴的x坐标为h。

三、对称轴的应用1. 确定顶点坐标：对称轴上的点到顶点的距离相等，因此可以通过对称轴的x坐标求出顶点的x坐标，然后代入函数式中求得顶点的y坐标。

2. 确定图像的对称性：通过对称轴的位置和性质，可以判断函数的图像是否沿着对称轴对称，从而帮助我们快速绘制出二次函数的图像。

3. 解二次方程：对称轴的特性可以帮助我们求解二次方程。

通过找到对称轴和顶点的坐标，我们可以得到二次函数的标准式，从而进一步求解相关问题。

综上所述，二次函数中的对称轴性质是十分重要的，它可以帮助我们更好地理解和运用二次函数。

通过对称轴的定义、性质和应用等方面的学习，我们可以在解题过程中更加灵活地运用这一性质，从而提高解题效率和准确性。

二次函数的顶点和对称轴二次函数是一种形式为f(x) = ax^2 + bx + c的函数，其中a、b、c是实数且a不等于0。

在二次函数的图像中，顶点和对称轴是两个重要的概念。

本文将对二次函数的顶点和对称轴进行讨论。

一、顶点的定义和性质二次函数的顶点是函数图像的最高点或最低点。

顶点的坐标为(xv, yv)，其中xv为顶点的横坐标，yv为顶点的纵坐标。

对于一般形式的二次函数f(x) = ax^2 + bx + c，顶点的横坐标可以通过公式xv = -b / (2a)计算得出。

将这个横坐标带入函数中，即可求得顶点的纵坐标yv。

顶点的性质包括以下几点：1. 当a大于0时，二次函数开口向上，顶点为函数图像的最低点。

当a小于0时，二次函数开口向下，顶点为函数图像的最高点。

2. 顶点对称于函数图像的对称轴。

对称轴是垂直于x轴的一条直线，它通过顶点并将函数图像分成对称的两部分。

对称轴的方程可以通过公式x = xv来表示，其中xv为顶点的横坐标。

二、对称轴的定义和性质对称轴是二次函数图像的特殊直线，它通过函数的顶点并将函数图像分成对称的两部分。

对称轴的方程为x = xv，其中xv为顶点的横坐标。

对称轴的性质包括以下几点：1. 对称轴是垂直于x轴的一条直线。

它与x轴的交点恰为顶点的横坐标。

2. 对称轴将函数图像分为两个关于对称轴对称的部分。

对于任意点(x, y)在对称轴上，对称轴上的另一个对应点为(-x, y)。

3. 对称轴上的点对应的函数值相等。

即对于任意点(x, y)在对称轴上，有f(x) = f(-x)。

三、顶点和对称轴的示例分析为了更好地理解顶点和对称轴的概念，我们来分析一个具体的例子：f(x) = 2x^2 + 4x - 3。

首先，计算顶点的横坐标xv。

根据公式xv = -b / (2a)，代入a = 2和b = 4，得到xv = -2 / (2*2) = -1/2。

然后，将顶点横坐标xv带入函数中，计算得到顶点的纵坐标yv。

一、二次函数性质1. 已知二次函数f(x) = ax^2 + bx + c，其中a、b、c为实数，且a ≠ 0。

若f(x)的对称轴为x = 1，且f(0) = 2，求f(x)的解析式。

2. 设二次函数f(x) = ax^2 + bx + c的图象开口向上，且f(1) = 3，f(1) = 1，求f(x)的解析式。

3. 已知二次函数f(x) = ax^2 + bx + c的图象与x轴有两个交点，且f(0) = 1，f(1) = 3，求f(x)的解析式。

4. 设二次函数f(x) = ax^2 + bx + c的图象开口向下，且f(1) = 3，f(1) = 1，求f(x)的解析式。

5. 已知二次函数f(x) = ax^2 + bx + c的图象与x轴有两个交点，且f(0) = 1，f(2) = 3，求f(x)的解析式。

二、二次函数图像1. 已知二次函数f(x) = ax^2 + bx + c的图象开口向上，且顶点坐标为(1, 2)，求f(x)的解析式。

2. 设二次函数f(x) = ax^2 + bx + c的图象开口向下，且顶点坐标为(1, 3)，求f(x)的解析式。

3. 已知二次函数f(x) = ax^2 + bx + c的图象与x轴有两个交点，且顶点坐标为(0, 1)，求f(x)的解析式。

4. 设二次函数f(x) = ax^2 + bx + c的图象开口向上，且顶点坐标为(2, 3)，求f(x)的解析式。

5. 已知二次函数f(x) = ax^2 + bx + c的图象开口向下，且顶点坐标为(1, 2)，求f(x)的解析式。

三、二次函数图像变换1. 已知二次函数f(x) = x^2的图象，求函数g(x) = (x 1)^2 + 2的图象。

2. 设二次函数f(x) = x^2的图象，求函数g(x) = (x + 2)^2 3的图象。

3. 已知二次函数f(x) = x^2的图象，求函数g(x) = (x 1)^22的图象。

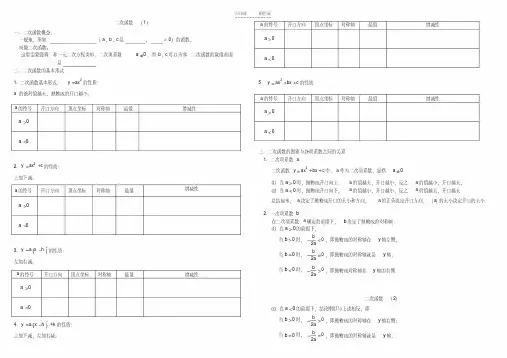
二次函数考点一 二次函数的定义1.形如 的函数是二次函数；2.二次函数的一般形式： ；3. 已知:二次函数22(2)32ky k x x -=--+ ，则k 的值是 ；考点二 二次函数、图像及其性质1、二次函数图像是一条 ；2、a值探究(1) 当a ＞0时，图像开口 ；当a ＜0时，图像开口 ； (2) a 的绝对值相等，则图像形状、大小相同（3）a 的绝对值越大，图像的开口越小；a 的绝对值越小，图像的开口越大3、c 值探究：二次函数与y 轴的交点坐标（ ， ）4、对称轴：（1）对称轴在y 轴左侧，则a 与b（2）对称轴在y 轴右侧，则a 与b 简称5、顶点坐标（ ）6、增减性：结合 开口 、对称轴 分析 如：7、最值：结合 开口 、顶点坐标 分析 如：8、平移：（1）首先化成顶点式 ；（2）应用左 右 ； 上 ，下 完成平移。

如：9、对称应用：（1）关于x 轴对称：（2）关于y 轴对称：考点三 二次函数常见形式图像及其性质1、2(0)y ax a =≠ 2、2(0)y ax c a =+≠ 3、2()(0)y a x h k a =-+≠ 4、2(0)y ax bx c a =++≠5、12()()(0)y a x x x x a =--≠考点三 用二次函数观点看一元二次方程1、 ∆>0 ⇔ 二次函数与X 轴有两个不同的交点坐标2、 ∆=0 ⇔ 二次函数与X 轴有一个交点坐标3、 ∆<0 ⇔ 二次函数与X 轴无交点坐标 应用举例：1、已知二次函数y=-x 2+3x+m 的部分图象如图1所示，则关于x 的一元二次方程-x 2+3x+m=0的解为________.2、小明从图2所示的二次函数2y ax bx c =++的图象中，观察得出了下面八条信息：①0c <；②0abc >；③0a b c -+>；④230a b -=；⑤40c b ->；⑥∆<0；⑦a b <；⑧ 420a b c -+>，你认为其中正确信息的个数有_____ （填序号）3、二次函数223y x x =--的图象如图所示．当y ＜0时，自变量x 的取值范围是考点四 实际问题和二次函数应1、小李想用篱笆围成一个周长为60米的矩形场地，矩形面积S （单位：平方米）随矩形一边长x （单位：米）的变化而变化．（1）求S 与x 之间的函数关系式，并写出自变量x 的取值范围；（2）当x 是多少时，矩形场地面积S 最大？最大面积是多少？图2图12、某旅行社有客房120间，每间客房的日租金为50元，每天都客满.旅社装修后要提高租金，经市场调查发现，如果每间客房的日租金每增加5元时，则客房每天出租数就会减少6间，不考虑其他因素，旅社将每间客房的日租金提高到多少元时，客房日租金的总收入最高？3、某商品的进价每件为50元，现在的售价为每件60元，每星期可卖出70件，市场调查反映：如果每件的售价每涨10元（售价每件不能高于140元），那么每星期少卖5件，设每件涨价x 元（x 为10的正整数倍），每周销售量为y 件 。

二次函数练习题及答案(解析版)一、选择题：1 下列关系式中，属于二次函数的是(x为自变量)( )2 函数y=x2-2x+3的图象的顶点坐标是( )A (1，-4) B(-1，2) C (1，2) D(0，3)23 抛物线y=2(x-3)的顶点在( )A 第一象限B 第二象限C x轴上D y轴上4 抛物线的对称轴是( )A x=-2 Bx=2 C x=-4 D x=45 已知二次函数y=ax2+bx+c的图象如图所示，则下列结论中，正确的是( )A ab>0，c>0B ab>0，c<0C ab<0，c>0D ab<0，c<06 二次函数y=ax2+bx+c的图象如图所示，则点在第___象限( )A 一B 二C 三D 四7 如图所示，已知二次函数y=ax2+bx+c(a≠0) 的图象的顶点P 的横坐标是4，图象交 x 轴于点A(m，0) 和点B ，且m>4，那么AB 的长是( )A 4+mB mC 2m-8D 8-2m8 若一次函数y=ax+b的图象经过第二、三、四象限，则二次函数y=ax2+bx的图象只可能是( )9 已知抛物线和直线在同一直角坐标系中的图象如图所示，抛物线的对称轴为直线x=-1，P 1(x1，y 1) ，P 2(x2，y 2) 是抛物线上的点，P3(x3，y 3) 是直线上的点，且-1A y110 把抛物线物线的函数关系式是( ) AC 的图象向左平移2个单位，再向上平移3个单位，所得的抛B D二、填空题：11 二次函数y=x2-2x+1的对称轴方程是______________12 若将二次函数y=x2-2x+3配方为y=(x-h)2+k的形式，则y=________13 若抛物线y=x2-2x-3与x 轴分别交于A 、B 两点，则AB 的长为_________14 抛物线y=x2+bx+c，经过A(-1，0) ，B(3，0) 两点，则这条抛物线的解析式为_____________15 已知二次函数y=ax2+bx+c的图象交x 轴于A 、B 两点，交y 轴于C 点，且△ABC 是直角三角形，请写出一个符合要求的二次函数解析式________________16 在距离地面2m 高的某处把一物体以初速度v 0(m/s)竖直向上抛物出，在不计空气阻力的情况下，其上升高度s(m)与抛出时间t(s)满足：(其中g 是常数，通常取10m/s2) 若v 0=10m/s，则该物体在运动过程中最高点距地面_________m17 试写出一个开口方向向上，对称轴为直线x=2，且与y 轴的交点坐标为(0，3) 的抛物线的解析式为______________18 已知抛物线y=x2+x+b2经过点，则y 1的值是_________三、解答题：19 若二次函数的图象的对称轴方程是，并且图象过A(0，-4) 和B(4，0) ，(1)求此二次函数图象上点A 关于对称轴对称的点A ′的坐标; (2)求此二次函数的解析式;20 在直角坐标平面内，点 O 为坐标原点，二次函数y=x2+(k-5)x-(k+4) 的图象交 x 轴于点A(x1，0) 、B(x2，0) ，且(x1+1)(x2+1)=-8 (1)求二次函数解析式;(2)将上述二次函数图象沿x 轴向右平移2个单位，设平移后的图象与y 轴的交点为C ，顶点为P ，求△POC 的面积21 已知：如图，二次函数y=ax2+bx+c的图象与x 轴交于A 、B 两点，其中A 点坐标为(-1，0) ，点C(0，5) ，另抛物线经过点(1，8) ，M 为它的顶点(1)求抛物线的解析式; (2)求△MCB 的面积S △MCB22 某商店销售一种商品，每件的进价为250元，根据市场调查，销售量与销售单价满足如下关系：在一段时间内，单价是1350元时，销售量为500件，而单价每降低1元，就可以多售出200件请你分析，销售单价多少时，可以获利最大二次函数练习题参考答案与解析一、选择题1 考点：二次函数概念选A2 考点：求二次函数的顶点坐标解析：法一，直接用二次函数顶点坐标公式求法二，将二次函数解析式由一般形式转换为顶点式，即y=a(x-h)2+k的形式，顶点坐标即为(h，k) ，y=x2-2x+3=(x-1)2+2，所以顶点坐标为(1，2) ，答案选C3 考点：二次函数的图象特点，顶点坐标解析：可以直接由顶点式形式求出顶点坐标进行判断，函数y=2(x-3)2的顶点为(3，0) ，所以顶点在x 轴上，答案选C4 考点：数形结合，二次函数y=ax2+bx+c的图象为抛物线，其对称轴为解析：抛物线，直接利用公式，其对称轴所在直线为答案选B5 考点：二次函数的`图象特征解析：由图象，抛物线开口方向向下，抛物线对称轴在y 轴右侧，抛物线与y 轴交点坐标为(0，c) 点，由图知，该点在x 轴上方，答案选C6 考点：数形结合，由抛物线的图象特征，确定二次函数解析式各项系数的符号特征解析：由图象，抛物线开口方向向下，抛物线对称轴在y 轴右侧，抛物线与y 轴交点坐标为(0，c) 点，由图知，该点在x 轴上方，在第四象限，答案选D7 考点：二次函数的图象特征解析：因为二次函数y=ax2+bx+c(a≠0) 的图象的顶点P 的横坐标是4，所以抛物线对称轴所在直线为x=4，交x 轴于点D ，所以A 、B 两点关于对称轴对称，因为点A(m，0) ，且m>4，所以AB=2AD=2(m-4)=2m-8，答案选C8 考点：数形结合，由函数图象确定函数解析式各项系数的性质符号，由函数解析式各项系数的性质符号画出函数图象的大致形状解析：因为一次函数y=ax+b的图象经过第二、三、四象限，所以二次函数y=ax2+bx的图象开口方向向下，对称轴在y 轴左侧，交坐标轴于(0，0) 点答案选C9 考点：一次函数、二次函数概念图象及性质解析：因为抛物线的对称轴为直线x=-1，且-1-1时，由图象知，y 随x 的增大而减小，所以y 210 考点：二次函数图象的变化抛物线平移2个单位得到，再向上平移3个单位得到的图象向左答案选C二、填空题11 考点：二次函数性质解析：二次函数y=x2-2x+1，所以对称轴所在直线方程答案x=112 考点：利用配方法变形二次函数解析式解析：y=x2-2x+3=(x2-2x+1)+2=(x-1)2+2答案y=(x-1)2+213 考点：二次函数与一元二次方程关系解析：二次函数y=x2-2x-3与x 轴交点A 、B 的横坐标为一元二次方程x 2-2x-3=0的两个根，求得x 1=-1，x 2=3，则AB=|x2-x 1|=4答案为414 考点：求二次函数解析式解析：因为抛物线经过A(-1，0) ，B(3，0) 两点，解得b=-2，c=-3，答案为y=x2-2x-315 考点：此题是一道开放题，求解满足条件的二次函数解析式，答案不唯一解析：需满足抛物线与x 轴交于两点，与y 轴有交点，及△ABC 是直角三角形，但没有确定哪个角为直角，答案不唯一，如：y=x2-116 考点：二次函数的性质，求最大值解析：直接代入公式，答案：717 考点：此题是一道开放题，求解满足条件的二次函数解析式，答案不唯一解析：如：y=x2-4x+318 考点：二次函数的概念性质，求值三、解答题19 考点：二次函数的概念、性质、图象，求解析式解析：(1)A′(3，-4)(2)由题设知：∴y=x2-3x-4为所求(3)20 考点：二次函数的概念、性质、图象，求解析式解析：(1)由已知x 1，x 2是x 2+(k-5)x-(k+4)=0的两根又∵(x1+1)(x2+1)=-8 ∴x 1x 2+(x1+x2)+9=0 ∴-(k+4)-(k-5)+9=0 ∴k=5 ∴y=x2-9为所求 (2)由已知平移后的函数解析式为： y=(x-2)2-9 且x=0时y=-5 ∴C(0，-5) ，P(2，-9)21 解： (1)依题意：(2)令y=0，得(x-5)(x+1)=0，x 1=5，x 2=-1 ∴B(5，0)由，得M(2，9)作ME ⊥y 轴于点E ，则可得S △MCB =1522 思路点拨：通过阅读，我们可以知道，商品的利润和售价、销售量有关系，它们之间呈现如下关系式：总利润=单个商品的利润×销售量要想获得最大利润，并不是单独提高单个商品的利润或仅大幅提高销售量就可以的，这两个量之间应达到某种平衡，才能保证利润最大因为已知中给出了商品降价与商品销售量之间的关系，所以，我们完全可以找出总利润与商品的价格之间的关系，利用这个等式寻找出所求的问题，这里我们不妨设每件商品降价x 元，商品的售价就是(135-x)元了单个的商品的利润是(135-x-25)这时商品的销售量是(500+200x)总利润可设为y 元利用上面的等量关式，可得到y 与x 的关系式了，若是二次函数，即可利用二次函数的知识，找到最大利润解：设销售单价为降价x 元顶点坐标为(425，91125)即当每件商品降价425元，即售价为135-425=925时，可取得最大利润91125元数学速算的技巧1、“凑整”先算1.计算：(1)24+44+56 (2)53+36+47解：(1)24+44+56=24+(44+56)=24+100=124因为44+56=100是个整百的数，所以先把它们的和算出来。

专题09二次函数的对称轴1．二次函数y ＝3x 2－6x －3图象的对称轴是_________.2．已知抛物线22y x mx =+-的对称轴为x=1，则m=______．3．若(2，5)，(4，5)是抛物线y ，ax 2，bx ，c 上的两个点，则抛物线的对称轴是（ ，A ．x =1B ．x =2C ．x =3D ．x =44．二次函数y ＝-x 2+（6-m ）x +8，当x ＞-2时，y 随x 的增大而减小；当x ＜-2时，y 随x 的增大而增大，则m 的值为（ ）A ．10B ．8C ．6D ．45．二次函数y=，x 2+，12，m，x+12，时，当x，2时，y 随x 的增大而减小；当x，2时，y 随x 的增大而增大，则m 的值为（ ）A ．6B ．8C ．10D ．126．二次函数23y x mx =-+，当x，2时，y 随x 的增大而减小；当x，2时，y 随x 的增大而增大，则当x=1时，y的值为， ，A ．8B ．3C ．2D ．07．抛物线y=-x2+bx+c 2y x bx c =-++的部分图像如图所示，则抛物线与x 轴的另一个交点坐标为_________．8．抛物线2y ax bx c =++经过()()3,1,5,1M N ，则抛物线的对称轴是__________．9．如图所示，抛物线2y x bx c =++的解析式为______________，对称轴为直线_____________，顶点坐标为_____________．10．抛物线y ＝ax 2﹣2ax+4(a ＞0)，下列判断正确的是( )A ．当x ＞2时，y 随x 的增大而增大B ．当x ＜2时，y 随x 的增大而增大C ．当x ＞1时，y 随x 的增大而增大D ．当x ＜1时，y 随x 的增大而增大11．二次函数y =ax 2+bx +3的图象经过点A (-1，0)，B (3，0)，那么一元二次方程ax 2+bx =0的根是_____． 12．某抛物线过点(3)t -，和(7)t ，，则它的对称轴为_________________．13．二次函数y ＝ax 2+bx +c 的图象与x 轴相交于（﹣1，0）和（5，0）两点，则该抛物线的对称轴是_____． 14．二次函数y=ax 2+bx+c 的图象与x 轴的交点为（-12,0）和（-4,0），则它的对称轴是直线________.15．已知点A （2,5），B （4,5）是抛物线24y x bx c =++上的两点，则这条抛物线的对称轴为直线__________.16．y ＝ax 2+bx+c 过点A （﹣1，0），B （3，0），则此抛物线的对称轴是直线x ＝_____．17．抛物线2y ax bx c =++与x 轴的公共点是()2,0-，()6,0，则此抛物线的对称轴是________．18．若抛物线2y x bx c =++与x 轴的两个交点坐标分别为（2，0），（4，0），则此抛物线的对称轴是______.19．已知抛物线25y ax bx =++的对称轴是1x =,若关于x 的方程2 70ax bx +-=的一个根是4,那么该方程的另一个根是__________．20．已知二次函数的图象经过点(1，3)和(3，3)，则此函数图象的对称轴与x 轴的交点坐标是___．21．二次函数y ＝x 2﹣bx +c 的图象上有两点A （3，﹣2），B （﹣9，﹣2），则此抛物线的对称轴是直线x ＝________． 22．已知抛物线2y ax bx c =++与x 轴的交点是()1,0-，()3,0，则这条抛物线的对称轴是________， 23．若()2,5、()4,5是抛物线2y ax bx c =++上的两个点，则它的对称轴是______.24．抛物线()()y 2x 1x 3=+-的对称轴是______．25．二次函数22(2)y x m =-+，当x>m+1时，y 随x 的增大而增大，当x<m+1时，y 随x 的增大而减小，则m 的值是_______．1．已知函数y ＝（x ﹣1）2，下列结论正确的是（ ）A ．当x ＞0时，y 随x 的增大而减小B ．当x ＜0时，y 随x 的增大而增大C ．当x ＜1时，y 随x 的增大而减小D ．当x ＜﹣1时，y 随x 的增大而增大 2．已知函数y=()2212x -++，当x ＞ 时，y 随x 的增大而减小．3．如图，抛物线2y ax bx c =++经过原点，当3x <时，y 的值随x 的增大而减小；当3x >时，y 的值随x 的增大而增大，若0y <，则x 的取值范围为________．4．已知二次函数y ＝(x ﹣2)2+3，当x ＜2时，y 随x 的增大而_____．(填“增大”或“减小”)5．已知二次函数y ＝（x ﹣2）2﹣3，当x ＜2时，y 随x 的增大而_____（填“增大”或“减小”）．6．已知函数y ＝2(x ﹣3)2+1，当_____(填写x 需满足的条件)时，y 随x 的增大而增大．7．已知二次函数y=-x 2+2x+5，当x________时，y 随x 的增大而增大8．已知二次函数y=﹣2x 2+x+4，当x ＜_____时，y 随x 的增大而增大．9．已知二次函数y=（x ﹣1）2+2，当x ＞1时，y 随x 的增大而 （填“减小”或“增大”）．10．二次函数y ＝﹣（x +5）2+7，当x __时，y 随x 的增大而增大，最值是__．11．二次函数y=3x 2-3的图象开口向_____，顶点坐标为_____，对称轴为_____，当x>0时，y 随x 的增大而_____；当x<0时，y 随x 的增大而_____.因为a=3>0，所以y 有最_____值，当x=_____时，y 的最_____值是_____. 12．抛物线2367y x x =-+，当x ______时，y 随x 的增大而增大，当x ______时，y 随x 的增大而减小. 13．已知函数22y x x =--，当 时，函数值y 随x 的增大而增大．14x 时，函数值随x 的增大而减小. 15．对于抛物线，当x 时，函数值y 随x 的增大而减小. 16．若二次函数y，ax 2，bx，c 的图象满足下列条件：(1)当x，2时，y 随x 的增大而增大；(2)当x≥2时，y 随x 的增大而减小．请写一个这样的二次函数解析式是________________，17．二次函数2-2-3y x x =中，当自变量x_____时，函数值y 随x 的增大而增大．。

二次函数值大小比较对称轴二次函数是一种常见的数学函数形式，可以用公式y=ax^2+bx+c 表示，其中a、b、c是常数，且a不等于零。

二次函数图像通常是一个U形的曲线，也称为抛物线。

在这篇文章中，我们将探讨以下几个方面：1.二次函数值大小比较2.对称轴一、二次函数值大小比较在比较两个二次函数的值的大小时，我们可以通过观察二次函数的系数a的正负来判断。

1.当a大于0时，代表抛物线开口朝上。

因此，二次函数的值随着自变量增大而增大，值随着自变量减小而减小。

换句话说，函数的最小值出现在对称轴的上方。

例如，对于函数f(x) = 2x^2+3x+1，当x>0时，f(x)值逐渐增大；当x<0时，f(x)值逐渐减小。

2.当a小于0时，代表抛物线开口朝下。

因此，二次函数的值随着自变量增大而减小，值随着自变量减小而增大。

换句话说，函数的最大值出现在对称轴的上方。

例如，对于函数g(x) = -2x^2-3x+1，当x>0时，g(x)值逐渐减小；当x<0时，g(x)值逐渐增大。

二、对称轴对称轴是二次函数图像的一条直线，具有对称性质。

对称轴可以通过计算公式中x的值来确定。

1.对于一般形式的二次函数y=ax^2+bx+c，对称轴的x坐标可以通过公式x=-b/(2a)计算得到。

例如，对于函数h(x) = 2x^2+4x-3，对称轴的x坐标为x=-4/(2*2)=-1。

这意味着对称轴与y轴的交点为(-1, 0)，抛物线在该点上下对称。

2.当二次函数通过顶点时，可以简化计算对称轴的方法。

顶点的x 坐标即为对称轴的x坐标。

例如，对于上述的函数f(x) = 2x^2+3x+1，顶点的x坐标为(-b/2a)=-3/4，因此对称轴的x坐标也是-3/4。

另外，二次函数的对称轴还具有以下几个性质：1.对称轴将抛物线分为两个对称的部分，左侧和右侧。

这意味着对称轴有助于我们了解函数的对称性质和图像的形状。

2.对称轴上的点是抛物线上最高点（当a<0）或最低点（当a>0）。

二次函数综合练习（1）一、填空题 1．抛物线22-=x y 的顶点坐标为（ ） 2．二次函数y=(x －3)(x ＋2)的图象的对称轴是（ ） 3．已知抛物线y=x 2－8x ＋c 的顶点在x 轴上，则c 的值是（ ）4．童装专卖店销售一种童装，若这种童装每天获利y （元）与销售单价x （元）满足关系 y=－x 2+50x －500，则要想获得最大利润每天必须卖出（ ） 5．二次函数y ＝x 2－2x+1与x 轴的交点个数是（ ） 6．若A(－134，y 1)、B(－1，y 2)、C(53，y 3)为二次函数y=－x 2－4x+5的图象上的三点，则y 1、y 2、y 3的大小关系是（ ）7．把抛物线y ＝2x 2先向左平移3个单位，向上平移4个单位，所得抛物线的函数表达式为（ ） 8．某大学的校门是一抛物线形水泥建筑物（如图所示），大门的地面宽度为8m ，两侧距地 面4米高处各有一个挂校名匾用的铁环，两铁环的水平距离为6 m ，则校门的高为（精 确到0.1 m ，水泥建筑物的厚度忽略不计）（ ）9．二次函数c bx ax y ++=2的图象如图所示，则abc ，ac b 42-，b a +2，c b a ++这四个式子中，值为正数的有（ ） 10．已知函数y=x 2－2x －2的图象如图2示，根据其中提供的信息，可求得使y ≥1成立的x的取值范围是（ ）第8题) (第9第11．抛物线2)3(94-=x y 与x 轴的交点为A ，与y 轴的交点为B ，则△AOB 的面积为 。

12．某二次函数的图象与x 轴交于点(－1，0)，(4，0)，且它的形状与抛物线y ＝－x 2形状相同。

则这个二次函数的解析式为 。

13．二次函数的图象经过三个定点（2，0），（3，0），（•0，-•1），则它的解析式为________，该图象的顶点坐标为__________．对称轴 14．当k=________时，直线x+2y+k+1=0和2x+y+2k=0的交点在抛物线y=-x 2上．15．已知二次函数y=x 2-2（k+1）x+k 2+2的图象与x 轴交点的横坐标分别为x 1，x 2，且（x 1+1）（x 2+1）=8，则k 的值为__________． 16．如果y 与x 2成正比例，并且它的图象上一点P 的横坐标a 和纵坐标b 分别是方程x 2-x-6=0的两根，那么这个函数的解析式为_________． 17．抛物线y=x 2-4x+11的对称轴是直线________，顶点坐标为________． 18．如果抛物线y=-23x 2+（m+2）x+27m 的对称轴为直线x=32，则m 的值为_________．19．把函数y=5x 2+10mx+n 的图象向左平移2个单位，向上平移3个单位，•所得图象的函数解析式为y=5x 2+30x+44，则m=_______，n=_______． 20．开口向下的抛物线y=a （x+1）（x-4）与x 轴交于A 、B 两点，与y•轴交于点C ．•若∠ACB=90°，则a 的值为________． 21．如图，二次函数y=x 2-ax+a-5的图象交x 轴于点A 和B ，交y 轴于点C ，当线段AB•的长度最短时，点C 的坐标为________． 22．在同一直角坐标系内，二次函数y 1=ax 2+bx+c 与y 2=cx 2+bx+a 的图象大致为（ ）23．在同一直角坐标系内，函数y=ax 2+bx 与y=b x（b ≠0）的图象大致为（ ）25．给出下列四个函数：y=-2x ，y=2x-1，y=3x （x>0），y=-x 2+3（x>0），其中y 随x•的增大而减小的函数有（ ）26．当m 取任何实数时，抛物线y=-2（x-m ）2-m 的顶点所在的直线为（ ） A ．x 轴 B ．y 轴 C ．y=x D ．y=-x27．当m 取任何实数时，抛物线y=-2（x+m ）2-m 2的顶点所在的曲线为（ ） A ．y=x 2 B ．y=-x 2 C ．y=x 2（x>0） D ．y=-x 2（x>0）28．已知抛物线y=ax 2+bx+c （a ≠0）与抛物线y=x 2-4x+3关于x 轴对称，则a 、b 、c•的值分别是（ ） A ．-1，4，-3 B ．-1，-4，-3 C ．-1，4，3 D ．-1，-4，3 29、.已知二次函数y =x 2+(2k +1)x +k 2－1的最小值是0，则k 的值是（ ）A.43 B.－43 C.45 D.－45二次函数综合练习（2）30．如果抛物线y=-23x 2+（m+2）x+27m 的对称轴为直线x=32，则m 的值为_________．31、如果抛物线y=x 2-6x+c-2的顶点到x 轴的距离是3,那么c 的值等于（ ）32、直线y=3x-3与抛物线y=x 2-x+1的交点的个数是( ).33.抛物线y=4x 2-1与y 轴的交点坐标是_________,与x 轴的交点坐标是_____. 34.在同一坐标系中，二次函数y=－21x 2，y=x 2，y=－3x 2的开口由大到小的顺序是______.35.已知抛物线y=－2(x+1)2－3，如果y 随x 的增大而减小，那么x 的取值范围是______ 36.函数y=34x －2－3x 2有最_ _值为___.37.函数y=21x 2+2x+1写成y=a(x －h)2+k 的形式是（ ）38.抛物线y=－2x 2－x+1的顶点在第_____象限（ ）39.不论m 取任何实数，抛物线y=a(x+m)2+m(a ≠0)的顶点都( )A.在y=x 直线上;B.在直线y=－x 上;C.在x 轴上;D.在y 轴上40、函数y=ax 2+bx+c(a ≠0)的图象经过原点和第一、三、四象限，则函数有最______值，且a________0，b________0，c__________0。

二次函数对称轴公式二次函数是高中数学中一个非常重要的概念。

在掌握二次函数的基本概念之后，我们需要了解二次函数的一些重要性质，其中之一就是对称轴。

对称轴是二次函数的一个非常重要的概念，它可以帮助我们更好地理解和分析二次函数的性质。

对称轴是二次函数图像的一条直线，它将二次函数图像分成两个对称的部分。

对称轴与二次函数图像有着非常紧密的联系，对称轴的位置可以帮助我们确定二次函数的图像形状和位置。

对称轴的位置可以通过二次函数的标准式来确定。

二次函数的标准式一般表示为y=ax²+bx+c，其中a、b、c是常数。

对称轴的位置可以通过以下公式来计算：x=-b/2a这个公式的意义是，对称轴的x坐标是二次函数的顶点的横坐标。

顶点是二次函数图像中最高点或最低点的位置，它对应着二次函数的最值。

因此，对称轴的位置可以帮助我们确定二次函数的最值。

对称轴的位置还可以帮助我们确定二次函数的图像形状。

如果a>0，那么二次函数的图像开口向上，对称轴在二次函数图像的下方；如果a<0，那么二次函数的图像开口向下，对称轴在二次函数图像的上方。

对称轴的位置也可以帮助我们确定二次函数的零点。

二次函数的零点是指在二次函数图像上，y=0时所对应的x值。

如果我们知道了对称轴的位置和二次函数的最值，就可以很容易地确定二次函数的零点。

因为对称轴将二次函数图像分成了两个对称的部分，所以二次函数的零点一定在对称轴的两侧。

对称轴是二次函数图像中非常重要的一个概念。

它可以帮助我们确定二次函数的最值、图像形状和零点。

掌握对称轴的位置计算公式，可以更好地理解和分析二次函数的性质。