高等代数知识点归纳.doc

大一高代知识点高等代数是大一数学课程中的一门重要课程，它是线性代数的延伸和拓展，具有广泛的应用领域。

本文将为大一学生总结高等代数中的一些重要知识点，以帮助他们更好地理解和掌握这门课程。

一、向量空间向量空间是高等代数的基础概念之一。

一个向量空间必须满足以下几个条件：1.封闭性：对于向量空间中的任意向量，其线性组合仍然在该向量空间中。

2.加法交换律和结合律：向量空间中的加法操作满足交换律和结合律。

3.零向量：向量空间中必须存在一个零向量，它与任意向量的加法操作结果为该向量本身。

4.负向量：对于向量空间中的任意向量，它必须存在一个相反向量，使得它们的加法结果为零向量。

5.标量乘法：向量空间中的向量可以与标量进行乘法操作。

二、线性相关与线性无关线性相关和线性无关是判断向量组是否具有独立性的重要概念。

1.线性相关：如果向量组中存在一个非零向量，可以表示为其他向量的线性组合，则称该向量组线性相关。

2.线性无关：如果向量组中的向量不能表示为其他向量的线性组合，则称该向量组线性无关。

三、矩阵与矩阵运算矩阵是高等代数中的另一个核心概念。

矩阵是由数个数按行列顺序排列而成的矩形数组。

矩阵运算包括以下几种：1.矩阵的加法：对应位置元素相加。

2.矩阵的数乘：每个元素乘以一个常数。

3.矩阵的乘法：满足左乘规则和右乘规则。

四、行列式行列式是矩阵的一个重要性质，它是一个标量值。

行列式的定义涉及矩阵的排列和元素的交换，计算行列式可以使用拉普拉斯展开定理或递推法。

五、特征值与特征向量特征值与特征向量是矩阵的另一项重要概念。

1.特征值：一个矩阵的特征值是使得该矩阵与其特征向量相乘得到的结果是特征向量的常数倍。

2.特征向量：一个矩阵的特征向量是在矩阵乘法下保持方向不变或者只伸缩的向量。

六、线性变换与线性方程组线性变换是指在向量空间中进行的保持加法和标量乘法的运算。

线性方程组是线性变换的一种具体表达形式，可以使用矩阵运算进行求解。

七、特殊矩阵在高等代数中还有一些特殊的矩阵：1.单位矩阵：对角线上的元素为1，其他元素为0。

大一高等代数期末考知识点高等代数作为大一学生必修的一门数学课程，是代数学的重要分支，是培养学生抽象思维和逻辑思维的基础。

本文将系统地总结大一高等代数知识点，以帮助同学们复习期末考试。

一、集合与二元关系1. 集合及其运算：包括集合的定义、集合之间的相等关系、子集与真子集、交集、并集、补集和差集等。

2. 二元关系：掌握关系的定义、域、逆关系、复合关系、等价关系和序关系的概念。

二、数系与复数1. 自然数、整数、有理数、实数和复数的定义及其性质。

2. 复数的运算：复数的加减乘除、乘方和开方。

三、代数式与多项式1. 代数式的概念：包括代数式、项、系数和次数等。

2. 多项式的运算：多项式的加减乘除以及整式化简。

3. 多项式的因式分解：二次、三次多项式的因式分解方法。

四、方程与不等式1. 一元一次方程和不等式：一元一次方程和不等式的解集、方程组与不等式组的解集。

2. 一元二次方程与不等式：二次方程和不等式的解集、因式分解法和配方法解方程和不等式。

3. 绝对值方程与不等式：绝对值方程和不等式的解集。

五、函数与图像1. 函数的概念：函数的定义、定义域、值域、图像和性质。

2. 基本初等函数：包括幂函数、指数函数、对数函数、三角函数和反三角函数等。

3. 函数的运算：函数的加减乘除、复合函数以及函数的逆。

六、行列式与矩阵1. 行列式的概念与性质：行列式的定义、性质、性质的运算规律。

2. 矩阵的概念与性质：矩阵的定义、矩阵的加法和数乘、矩阵的乘法、矩阵的转置和矩阵的逆运算。

3. 线性方程组：线性方程组的定义、增广矩阵、齐次方程组与非齐次方程组。

七、向量与线性空间1. 向量的概念与运算：向量的定义、向量的加法、数乘和数量积。

2. 线性空间的概念与性质：线性空间的定义、线性空间的性质、线性相关与线性无关、线性空间的基与维数。

3. 子空间与线性变换：子空间的定义、子空间的性质、线性变换的定义、线性变换的性质。

八、特征值与特征向量1. 特征值与特征向量的概念：矩阵的特征值与特征向量的定义。

1122,,0,.i j i j in jn A i j a A a A a A i j ⎧=⎪++=⎨≠⎪⎩L==()mn A O A A O A BO BO BBO A AA B B O B O*==**=-1(1)211212112111()n n nnn n n n n n n a Oa a a a a a a Oa O---*==-K N N 1范德蒙德行列式：()1222212111112n i j nj i nn n n nx x x x x x x x x x x ≤<≤---=-∏L L L M M M L111代数余子式和余子式的关系：(1)(1)i j i j ij ijij ij M A A M ++=-=-分块对角阵相乘：11112222,A B A B A B ⎛⎫⎛⎫==⎪ ⎪⎝⎭⎝⎭⇒11112222A B AB A B ⎛⎫= ⎪⎝⎭,1122nn n A A A ⎛⎫= ⎪⎝⎭分块矩阵的转置矩阵：TTT TT A B A C C D BD ⎛⎫⎛⎫= ⎪ ⎪⎝⎭⎝⎭()1121112222*12n Tn ijn n nn A A A A A A A A A A A ⎛⎫ ⎪ ⎪== ⎪⎪⎝⎭LL M M M L ，ij A 为A 中各个元素的代数余子式. **AA A A A E ==,1*n A A -=, 11A A --=.分块对角阵的伴随矩阵：***A BA B AB ⎛⎫⎛⎫=⎪ ⎪⎝⎭⎝⎭111A B BA---⎛⎫⎛⎫= ⎪⎪⎝⎭⎝⎭ 1231111213a a a a a a -⎛⎫⎛⎫ ⎪ ⎪=⎪ ⎪ ⎪⎪ ⎪⎝⎭⎝⎭3211111213a a a a a a -⎛⎫⎛⎫⎪⎪=⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭矩阵的秩的性质：① ()A O r A ≠⇔≥1; ()0A O r A =⇔=;0≤()m n r A ⨯≤min(,)m n④ ()(),,()0m n n s r A r B n A B r AB B Ax ⨯⨯+≤⎧=⇒⎨=⎩若若0的列向量全部是的解⑤ ()r AB ≤{}min (),()r A r B⑥ 若P 、Q 可逆，则()()()()r A r PA r AQ r PAQ ===； 即：可逆矩阵不影响矩阵的秩.⑦ 若()()()m n Ax r AB r B r A n AB O B O A AB AC B C ο⨯⇔=⎧⎪=⎧⎪=⎨⎪⇒=⇒=⎧⎨⎪⎨⎪⎪=⇒=⎩⎩⎩ 只有零解在矩阵乘法中有左消去律；若()()()n s r AB r B r B n B ⨯=⎧=⇒⎨⎩ 在矩阵乘法中有右消去律.⑧ ()rr E O E O r A r A A OO OO ⎛⎫⎛⎫=⇒⎪ ⎪⎝⎭⎝⎭若与唯一的等价，称为矩阵的等价标准型. ⑨ ()r A B ±≤()()r A r B +, {}max (),()r A r B ≤(,)r A B ≤()()r A r B +⑩ ()()A O O A r r A r B O B B O ⎛⎫⎛⎫==+ ⎪ ⎪⎝⎭⎝⎭, ()()A C r r A r B O B ⎛⎫≠+ ⎪⎝⎭①n 个n 维线性无关的向量,两两正交,每个向量长度为1. ③(,)0αβ=. 记为：αβ⊥④21ni i a α====∑⑤1α==. 即长度为1的向量.内积的性质：① 正定性② 对称性③ 线性性12n A λλλ=L 1ni A λ=∑tr ，A tr 称为矩阵A 特征值与特征向量的求法(1) 写出矩阵A 的特征方程0A E λ-=，求出特征值i λ. (2) 根据()0i A E x λ-=得到 A 对应于特征值i λ的特征向量.设()0i A E x λ-=的基础解系为 12,,,i n r ξξξ-L 其中()i i r r A E λ=-. 则A 对应于特征值i λ的全部特征向量为1122,i i n r n r k k k ξξξ--+++L 其中12,,,in r k k k -L 为任意不全为零的数.3. ①1P AP B -= （P 为可逆矩阵）②1P AP B -= （P 为正交矩阵）③A 与对角阵Λ相似.（称Λ是A 7. 矩阵对角化的判定方法① n 阶矩阵A 可对角化 (即相似于对角阵) 的充分必要条件是A 有n 个线性无关的特征向量. 这时,P 为A 的特征向量拼成的矩阵，1P AP -为对角阵,主对角线上的元素为A 的特征值. 设i α为对应于i λ的线性无关的特征向量,则有：121n P AP λλλ-⎛⎫⎪⎪= ⎪ ⎪⎝⎭O .② A 可相似对角化⇔()i i n r E A k λ--=，其中i k 为i λ的重数⇔A 恰有n 个线性无关的特征向量.○注：当iλ=0为A 的重的特征值时，A 可相似对角化⇔i λ的重数()n r A =-=Ax ο=基础解系的个数.③ 若n 阶矩阵A 有n 个互异的特征值⇒A 可相似对角化. 正交矩阵 T AA E =③ 正交阵的行列式等于1或-1； ⑤ 两个正交阵之积仍是正交阵；⑥ A 的行（列）向量都是单位正交向量组.施密特正交规范化 123,,ααα线性无关,112122111313233121122(,)(,)(,)(,)(,)(,)βααββαβββαβαββαββββββ=⎧⎪⎪⎪=-⎨⎪⎪=--⎪⎩正交化单位化：111βηβ= 222βηβ= 333βηβ=1. ① 二次型 11121121222212121112(,,,)(,,,)n n n n Tn ij i j n i j n n nn n a a a x a a a x f x x x a x x x x x x Ax a a a x ==⎛⎫⎛⎫ ⎪⎪⎪ ⎪=== ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭∑∑L L L L L L L L L L其中A 为对称矩阵，12(,,,)T n x x x x =L② A 与B 合同 TC AC B =. （,,A B C 为实对称矩阵为可逆矩阵）求C (A I)→(B C^T) 这个变换先进行行变换 再进行一致的列变换 最后 求得C 和C^T③ 正惯性指数 二次型的规范形中正项项数p 负惯性指数二次型的规范形中负项项数r p - ④ 两个矩阵合同⇔它们有相同的正负惯性指数⇔他们的秩与正惯性指数分别相等. ⑤ 两个矩阵合同的充分条件是：A 与B 等价 ⑥ 两个矩阵合同的必要条件是：()()r A r B =2. 12(,,,)Tn f x x x x Ax =L 经过合同变换可逆线性变换x Cy = 化为21ni i f d y =∑标准形.① 正交变换法② 配方法（1）若二次型含有i x 的平方项，则先把含有i x 的乘积项集中，然后配方，再对其余的变量同样进行， 直到都配成平方项为止，经过非退化线性变换，就得到标准形;（2） 若二次型中不含有平方项，但是0ij a ≠ (i j ≠), 则先作可逆线性变换()1,2,,,i i j j i jkk x y y x y y k n k i j x y=-⎧⎪=+=≠⎨⎪=⎩L 且,3.12,,,n x x x L 不全为零，12(,,,)n f x x x >L 0.正定二次型对应的矩阵.4. ()Tf x x Ax =为正定二次型⇔（之一成立）： （1） x ο∀≠ ，Tx Ax >0； （2）A 的特征值全大于0； （3）f 的正惯性指数为n ； （4）A 的所有顺序主子式全大于0；（5）A 与E 合同，即存在可逆矩阵C 使得TC AC E =； （6）存在可逆矩阵P ，使得TA P P =；(),nT A r A n A A Ax x Ax A Ax A A A E οοοββ==⇔∀≠≠≠⇔∀∈=≅可逆的列（行）向量线性无关 的特征值全不为0 只有零解 ，0总有唯一解 是正定矩阵 R 12,s iA p p p p nB AB E AB E⎧⎪⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪=⋅⋅⋅⎪==⎪⎩ 是初等阵存在阶矩阵使得 或 ()A r A n A A A Ax A ολ<=⇔==不可逆 0的列（行）向量线性相关 0是的特征值 有非零解,其基础解系即为关于0的⎧⎪⎪⎪⎨⎪⎪⎪⎩特征向量。

高等代数复习资料高等代数是大学数学中的一门重要课程，它是线性代数的延伸和拓展，涉及到向量空间、矩阵理论、线性变换等内容。

熟练掌握高等代数的基本概念和方法对于学习数学、物理、经济学等领域都具有重要意义。

本文档将为大家提供高等代数复习资料，帮助你巩固和复习相关知识。

第一部分：向量空间向量空间是高等代数中的重要概念，它是一种具有加法和数乘运算的集合。

理解向量空间的基本性质和运算规则是高等代数学习的基础。

在复习向量空间时，可以重点关注以下内容：1. 向量空间的定义和性质：了解向量空间的定义，包括加法和数乘的性质，以及满足的几个条件。

掌握零向量、加法逆元等概念。

2. 子空间：理解子空间的概念，包括子空间的闭性、加法和数乘的封闭性等。

重点掌握如何判断一个集合是否为子空间。

3. 线性相关性和线性无关性：了解线性相关和线性无关的概念，以及线性相关性和线性无关性的判别标准。

学习如何求解线性方程组。

第二部分：矩阵理论矩阵是高等代数中的重要工具，它用于表示线性变换和解决线性方程组。

学习矩阵理论可以帮助我们更好地理解向量空间和线性变换。

在复习矩阵理论时，可以关注以下内容：1. 矩阵的运算：了解矩阵的加法、数乘和乘法等运算规则。

掌握矩阵的转置、逆和行列式等概念。

2. 线性变换和矩阵表示：理解线性变换与矩阵之间的关系，学习如何通过矩阵表示线性变换。

3. 线性方程组与矩阵：掌握使用矩阵解决线性方程组的方法，包括高斯消元法和矩阵的逆等。

第三部分：线性变换线性变换是高等代数的核心内容，它描述了向量空间中的数学变换。

理解线性变换的基本概念和性质对于学习高等代数非常重要。

在复习线性变换时，可以关注以下内容：1. 线性变换的定义和性质：了解线性变换的定义，包括保持加法和数乘运算、保持零向量等性质。

2. 线性变换的矩阵表示：了解线性变换与矩阵之间的关系，学习如何通过矩阵表示线性变换。

3. 特征值和特征向量：掌握特征值和特征向量的概念，学习如何求解特征值和特征向量。

数学高等代数重点知识点数学高等代数是大学阶段数学学科的重要组成部分，它涵盖了众多的数学概念、理论和技巧。

本文将聚焦于数学高等代数的重点知识点，旨在帮助读者全面理解和掌握这些知识。

一、矩阵和行列式1. 矩阵的基本概念：矩阵是由数个数按一定规律排成的矩形阵列。

介绍矩阵的行、列、元素、维数等概念。

2. 矩阵的运算：包括矩阵的加法、减法、数乘以及矩阵的乘法等。

3. 矩阵的转置：介绍矩阵的转置操作及其性质。

4. 行列式的定义和性质：解释行列式的概念，阐述行列式的性质和运算规则。

二、向量空间1. 向量的基本概念：阐述向量的定义、线性运算以及向量的线性相关性。

2. 向量空间的定义和性质：解释向量空间的概念，介绍向量空间的性质和基本运算规则。

3. 子空间：介绍子空间的定义，解释子空间的性质和判定标准。

4. 基和维数：讲解基的概念，介绍线性无关和生成空间的概念，并介绍维数的定义和计算方法。

三、线性方程组1. 线性方程组的基本概念：解释线性方程组的定义和基本性质。

2. 解的存在性与唯一性：介绍线性方程组解的存在性、唯一性和无穷多解的判定条件。

3. 齐次线性方程组和非齐次线性方程组：解释齐次线性方程组和非齐次线性方程组的概念，介绍它们解的性质。

4. 矩阵的秩和可逆性：介绍矩阵的秩的概念，解释矩阵可逆的条件和性质。

四、特征值和特征向量1. 特征值和特征向量的定义：解释特征值和特征向量的概念，说明与矩阵的关系。

2. 特征方程：介绍特征方程的定义和求解方法。

3. 对角化和相似矩阵：解释相似矩阵和对角矩阵的概念，介绍矩阵相似的判定条件和对角化的步骤。

五、线性映射1. 线性映射的定义和性质：解释线性映射的概念，介绍线性映射的基本性质和运算规则。

2. 核和像：介绍线性映射的核（零空间）和像（值域）的概念。

3. 矩阵的表示和变换：解释线性映射的矩阵表示方法，介绍线性映射的变换和判定条件。

综上所述，数学高等代数的重点知识点包括矩阵和行列式、向量空间、线性方程组、特征值和特征向量以及线性映射等内容。

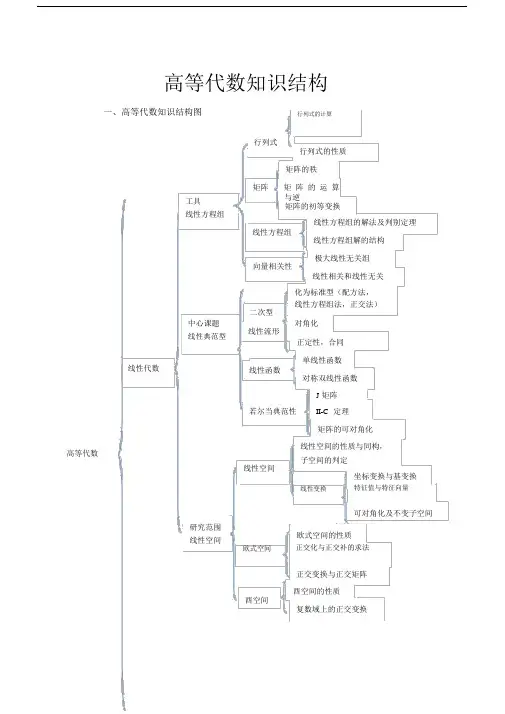
高等代数知识结构一、高等代数知识结构图行列式的计算工具线性方程组中心课题线性典范型线性代数高等代数研究范围线性空间行列式行列式的性质矩阵的秩矩阵矩阵的运算与逆矩阵的初等变换线性方程组的解法及判别定理线性方程组线性方程组解的结构极大线性无关组向量相关性线性相关和线性无关化为标准型（配方法，线性方程组法，正交法）二次型对角化线性流形正定性，合同单线性函数线性函数对称双线性函数J矩阵若尔当典范性II-C 定理矩阵的可对角化线性空间的性质与同构，子空间的判定线性空间坐标变换与基变换线性变换特征值与特征向量可对角化及不变子空间欧式空间的性质欧式空间正交化与正交补的求法正交变换与正交矩阵酉空间的性质酉空间复数域上的正交变换最大公因式定理整除理论互素与同于因式分解唯一性因式分解理论重因式多项式理论复数域多项式根的理论实数域求法有理数域判定（爱绅斯坦因）多元多项式 /根的判别式对称多项式韦达定理二、高等代数知识结构内容（一）线性代数：工具：线性方程组1. 行列式：a11 a12a1n1 行列式的计算设有n2个数，排成 n 行 n 列的数表a21a22a2n ，即 n 阶行an1an 2ann列式．这个行列式等于所有取自不同行不同列的n 个元素的乘积a1j1a2 j2anj n⑴的代数和，这里j1 j2j n是1，2，，n的一个排列,每一项⑴都按下列规则带有符号：当 j1 j 2j n是偶排列时,⑴带正号；当j1j2j n是奇排列时,⑴带负号．即aa11a12a1n21a22 a2 n1 j 1j2 j na 1j 1a2 j 2anj n ，这里=表示j 1 j 2j nj 1 j 2 j nan1an 2ann对所有 n 级排列求和 .a. 行列式的性质：性质 1. 行列互换，行列式不变。

性质 2. 一行的公因子可以提出来（或以一数乘行列式的一行就相当于用这个数乘此行列式。

性质 3. 如果某一行是两组数的和，那么这个行列式就等于两个行列式的和，而这两个行列式除这一行以外与原行列式的对应行一样。

高等代数重点知识点总结归纳10点
1. 函数：定义、概念、性质、图像及性质、偏导数、复合函数、极限、不等式及其解法、积分
2. 向量：概念、加减法及其性质、数量积、模与方向角、标准基、矩阵、线性方程组
3. 曲线：曲线的概念及性质、曲线的根的计算、曲线的切线、曲线的端点与拐点
4. 数列：求和公式、等差数列和等比数列的性质、数列的通项公式
5. 概率：概率及性质、独立性、条件概率、随机变量、分布函数、期望
6. 几何：几何定义与性质、点、线、平面、空间三角形和多边形的性质、圆、椭圆、抛物线、双曲线、圆锥曲线
7. 系统方程：一元、多元方程组的求根法及其原理
8. 函数逆函数：函数的逆函数及其图像、求逆函数的方法
9. 向量函数：向量函数的定义、性质、积分
10. 偏微分：偏微分的概念、作用、求最值的过程。

第一章基本概念1.1集合Z表示全体整数的集合Q表示全体有理数的集合R表示全体实数的集合C表示全体复数的集合。

德.摩根（De Morgan）律对于任意集合ABC来说第一：集合C减去集合A与集合B的交集等于集合C减去集合A与集合C减去集合B的并集用数学符号表示为C-(A∩B)=(C-A) ∪（C-B）第二：集合C减去集合A与集合B的并集等于集合C减去集合A与集合C减去集合B的交集用数学符号表示为C-(A∪B)=（C-A）∩（C-B）元素属于集合用”∈”\符号，集合属于集合用 符号1.2映射映射：设AB是两个非空集合，A到B的一个映射指的是一个对应法则，通过这个法则，对于集合A中每一个元素x，有集合B中唯一确定的元素y与之对应。

（映射可以多对一，但是不允许一对多）满射：设f是A到B的一个映射，如果f(A)=B，那么就称f是A到B的一个满射。

单射：设f：A到B是一个映射，如果对于A中任意两个元素x1,x2只要有x1≠x2，就有f(x1)≠f(x2)，那么就称f是A到B的一个单射。

映射之间是可以合成的，具体不做解释。

双射：如果一个映射既是满射，又是单射，那么我们将这个映射称为双射。

本单元的题型大多为证明双射，所以这里要注意。

证明双射的步骤：第一步首先证明满射，将x用y来表示，然后将用y表示的x代入原方程中。

如果得到的结果等于y，那么即可证明该映射为满射。

第二步证明单射，将x1和x2代入方程中，并将含x1和x2的两个方程联立，如果解得x1等于x2，那么即可证明该映射为单射。

第三步，既是满射又是单射的映射即为双射，命题得证。

1.3 数学归纳法数学归纳法的原理是最小数原理最小数原理：正整数集N*的任意一个非空子集S必含有一个最小数，也就是这样一个数a ∈S，对于任意c∈S都有a≤c。

需要注意的是最小数原理并不是对于所有集合成立的。

例如全体整数集Z就没有最小数。

分数组成的集合也没有最小数。

然后就是本节的重点数学归纳法。

（1 ）定义：由s⋅ n个数a ij（i= 1,2, s；j= 1,2, n）排成s行n列的数表a 11a s1a1n，称为s行n列矩阵，简记为A= (a ij)s⋅n。

asn（2）矩阵的相等：设A= (a ij)m⋅n，B= (a ij)l⋅k，如果m= l，n= k，且a ij= b ij，对i= 1,2, m；j= 1,2, n都成立，则称A与B相等，记A= B。

（3）各种特殊矩阵：行矩阵，列矩阵，零矩阵，方阵，（上）下三角矩阵，对角矩阵，数量矩阵，单位矩阵。

a11（1）矩阵的加法：as1运算规律：①A+ B= B+ A②( A+ B) + C= A+ (B+ C)a11（2）数与矩阵的乘法：kas1 运算规律：①(k+ l) A= kA+ lA a1nb11b1na11+ b11+ =asnbs1bsnas1+ bs1③A+ O= A④A+(−A) = Oa1nka11ka1n=asnkas1kasn③k(lA) = (kl) Aa1n+ b1n。

a sn+b sn②k( A+ B) = kA+ kBa11 （3）矩阵的乘法：as1④A+(−A) = Oa1nb11b1mc11=asnbn1bnmcs1c1m其中csmc = a b + a b + + a b a 11ij i 1 1i i 2 2i in nj ，i = 1,2, s ； j = 1,2, m 。

运算规律：① ( A B )C = A (BC ) ③ (B + C ) A = BA + CA② A (B + C ) = AB + AC ④ k ( A B ) = A (kB ) = (kA )B 一般情况 ，① AB ≠ BA② AB = AC ， A ≠ 0 ， ⇒ B = C ③ AB = 0 ⇒ A = 0 或 A = 0a 11a 1na 11 a1s（4）矩阵的转置 ： A = ，A 的转置就是指矩阵 A '=a s 1asna n 1ans运算规律 ：① ( A ')'= A③ ( A B )'= B ' A '② ( A + B )'= A '+B '（5）方阵的行列式 ：设方阵 A =运算规律： ④ (kA )'= kA 'a 1n a11，则A 的行列式为| A |=。

高等代数复习提纲一． 多项式1. 带余除法—->辗转相除法- 1uf vg +=的运用2. 不可约多项式,标准分解式，特别是实数域和复数域情形。

3. 根与标准分解式(复数域）,重因式判定。

4. 有理根计算。

Eisenstein 判别法变形运用。

二． 行列式基本性质与算法, 行列式仅是后继高代内容的研究工具。

三． 线性方程组核心内容。

线性相关性判定及线性组合方式计算是两个核心概念。

1. 消元法:初等行变换是代数最基本方法。

2. 向量组线性相关性概念,秩的计算，矩阵非零r 级子式计算,极大无关组的求法。

3. 方程组三种等价形式的运用。

4. 线性方程组有解判别定理与向量组秩关系。

5. 解的结构与极大无关组。

四． 矩阵1. 矩阵乘积的秩。

2. 逆矩阵计算3. 初等变换与初等矩阵:左乘变行,右乘变列。

4. 分块的思想：与矩阵乘积,方程组关系等。

五． 二次型1. 二次型几何意义。

2. 二次型矩阵,标准型计算。

合同概念。

3. 规范形几何意义。

特别是实二次型。

4. 正定性的判定。

与向量内积关系等:例如: ()();T r A r A A =T A A 正定当且仅当0AX =只有零解,其中A 不必是方阵。

六 线性空间１. 线性空间定义。

2. 基（维数)，坐标，同构.n V P ≅3. 向量组线性相关性判定⇔同构坐标向量组相关性⇔ 线性方程组。

４. 子空间的交与和基的计算，维数公式。

5. 直和：交为{0}.七．线性变换1. 线性变换矩阵表示:线性变换=矩阵(基固定）,这一相等保持线性关系和乘积,从而一切关于线性变换问题完全等价于一个矩阵问题。

2. 基变换前后矩阵相似。

３. 特征值,特征向量的计算和性质。

注意特征向量和特征向量坐标的区别：首先计算的是特征向量坐标!４．可对角化判定。

值域与核的基的计算，“维数公式“。

八.λ矩阵１. 初等变换注意事项。

2. 标准型计算:简便算法。

３．行列式因子，不变因子,初等因子，Joｒｄaｎ块之间对应关系。

第一章 基本概念1.5 数环和数域定义1 设S 是复数集C 的一个非空子集,如果对于S 中任意两个数a 、b 来说，a+b,a-b,ab都在S 内，那么称S 是一个数环。

定义2 设F 是一个数环。

如果（i ）F 是一个不等于零的数； （ii ）如果a 、b ∈F,，并且b 0≠，aF b∈，那么就称F 是一个数域。

定理 任何数域都包含有理数域，有理数域是最小的数域。

第二章 多项式2.1 一元多项式的定义和运算定义1 数环R 上的一个文字的多项式或一元多项式指的是形式表达式()1 2012n n a a x a x a x ++++，是非负整数而012,,,n a a a a 都是R 中的数。

项式()1中，0a 叫作零次项或常数项，ii a x 叫作一次项，一般，i a 叫作i 次项的系数。

定义2 若是数环R 上两个一元多项式()f x 和()g x 有完全相同的项，或者只差一些系数为零的项，那么就说()f x 和()g x 就说是相等()()f x g x =定义3 nn a x 叫作多项式2012n n a a x a x a x ++++，0n a ≠的最高次项，非负整数n 叫作多项式2012n n a a x a x a x ++++，0n a ≠的次数。

定理2.1.1 设()f x 和()g x 是数环R 上两个多项式，并且()0f x ≠，()0g x ≠，那么 ()i 当()()0f x g x +≠时， ()()()()()()()()0max ,;f x g x f x g x ∂+≤∂∂()ii ()()()()()()()0f xg x f x g x ∂=∂+∂。

多项式的加法和乘法满足以下运算规则：1） 加法交换律：()()()()f x g x g x f x +=+；2） 加法结合律：()()()()()()()()f xg xh x f x g x h x ++=++； 3）乘法交换律：()()()()f x g x g x f x =； 4） 乘法结合律：()()()()()()()()f xg xh x f x g x h x =； 5） 乘法对加法的分配律：()()()()()()()()f x g x h x f x g x f x h x +=+。