5最标准全面的马尔可夫模型例题(以中天会计事务所为例)

马尔可夫链模型简介设考察对象为一系统,若该系统在某一时刻可能出现的事件集合为,}{N N E E E E E E ⋅⋅⋅⋅⋅⋅,2,1,2,1,两两互斥,则陈i E 为状态。

N i ⋅⋅⋅=,2,1。

称该系统从一种状态i E 变化到另一状态j E 的过程称为状态转移，并把整个系统不断实现状态转移的过程称为马尔可夫过程。

定义1 具有下列两个性质的马尔可夫过程称为马尔可夫链： （1）无后效性，即系统的第n 次实验结果出现的状态，只与第1-n 次有关，而与它以前所处的状态无关；（2）具有稳定性，该过程逐渐趋于稳定状态，而与初始状态无关。

定义2 向量),,,(21n u u u u ⋅⋅⋅= 成为概率向量，如果u 满足：⎪⎩⎪⎨⎧=⋅⋅⋅=≥∑=nj jj u nj u 11,,2,10 定义3 如果方阵P 的每行都为概率向量，则称此方阵为概率矩阵。

如果矩阵A 和B 皆为概率矩阵，则AB ，k A ，k B 也都是概率矩阵（k 为正整数）。

定义4 系统由状态i E 经过一次转移到状态j E 的概率记为ij P ，称矩阵⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅=3212222111211N N N N N P P P P P P P P P P 为一次（或一步）转移矩阵。

转移矩阵必为概率矩阵，且具有以下两个性质： 1、P P P k k )1()(-=； 2、k k P P =)(其中)(k P 为k 次转移矩阵。

定义5 对概率矩阵P ，若幂次方)(m P 的所有元素皆为正数，则矩阵P 称为正规概率矩阵。

（此处2≥m ）定理1 正规概率矩阵P 的幂次方序列P ，2P ，3P ，…趋近于某一方阵T ，T 的每一行均为同一概率向量t ，且满足t tP = 。

马尔可夫链模型如下：设系统在0=k 时所处的初始状态 ),,()0()0(2)0(1)0(N S S S S ⋅⋅⋅=为已知，经过k 次转移后的状态向量 ),,()()(2)(1)(k N k k k S S S S ⋅⋅⋅=),2,1(⋅⋅⋅=k ，则⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅=NN N N N N k P P P P P P P P P S S 212222111211)0()( 此式即为马尔可夫链预测模型。

中天会计事务所马尔可夫模型例题一、问题分析中天会计事务所由于公司业务日益繁忙，常造成公司事务工作应接不暇，解决该公司出现的这种问题的有效办法是要实施人力资源的供给预测技术。

根据对该公司材料的深入分析，可采用马尔可夫模型这一供给预测方法对该事务所的人力资源状况进行预测。

马尔可夫分析法是一种统计方法，其方法的基本思想是：找出过去人力资源变动的规律，用以来推测未来人力变动的趋势。

马尔可夫分析法适用于外在环境变化不大的情况下，如果外在环境变化较大的时候这种方法则难以用过去的经验情况预测未来。

马尔可夫分析法的分析过程通常是分几个时期来收集数据，然后在得出平均值，利用这些数据代表每一种职位的人员变动频率，就可以推测出人员的变动情况。

二、项目策划（一）第一步是编制人员变动概率矩阵表。

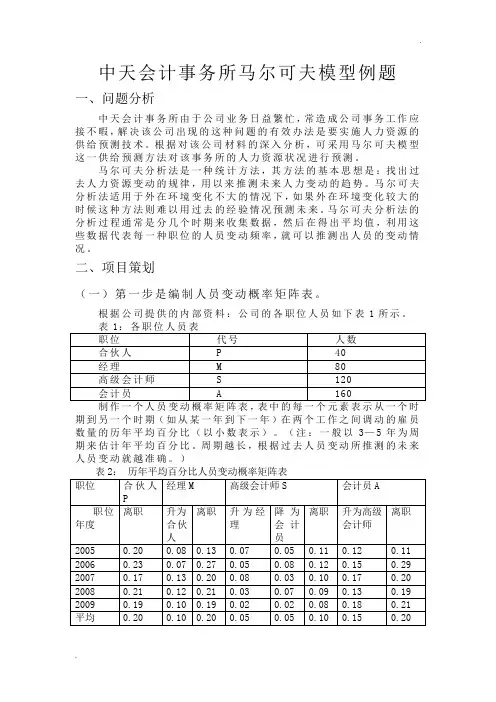
根据公司提供的内部资料：公司的各职位人员如下表1所示。

期到另一个时期（如从某一年到下一年）在两个工作之间调动的雇员数量的历年平均百分比（以小数表示）。

（注：一般以3—5年为周期来估计年平均百分比。

周期越长，根据过去人员变动所推测的未来人员变动就越准确。

）（二）第二步是编制人员变动矩阵表。

将上面的表2做成一个人员变动矩阵表，其具体过程是将中天会计事务所各个阶层员工流动的概率与各职位人数分别相乘即可预测出下一期人员可能调动的情况如下表3所示。

内，而有20%离职。

在任何一年里，平均65%的会计员留在原岗位工作，15%提升为高级会计师，20%离职。

这些历史数据代表了每一种工作中人员变动的概率。

（三）第三步是预测未来的人员变动（供给量）情况。

将计划初期每一种工作的人员数量与每一种工作的人员变动概率相乘，然后纵向相加，即得出表4的组织内部未来劳动力的净供给量。

（四）第四步是该会计事务所的某一期预测如上表4所示。

1、如上表4所示，会计员离职人数最多，离职率也最高，这说明这一职位在将来会出现短缺的现象，据此公司可采取以下具体的对策：①查明公司会计员离职率高的原因，采取必然的措施尽快地降低离职率②加大对公司会计员的培训力度，使他们尽快地晋升为会计师③采取多种方式，广开人员补充的渠道，吸引更多的专业人才补充岗位空缺。

马尔可夫决策规划第五讲 有限阶段模型及其他有限阶段模型的目标只有有限项，即1110210100P P P P P P P )(2)(+-++++=n n n f f f f f n f f f f f f n r r r r V βββπβ1) 当n 充分大时，近似令∞=n 2) 用动态规划法求解注意：用Bellmon 最优化原理可推出平稳策略优势。

§ 5.1 向后归纳法在确定性动态规划问题求解中，向后归纳法是寻求最优策略的一种有效解法，同样也是求解有限阶段Markov 决策规划问题中最优策略与最优值函数的有效解法。

定理5.1 在状态集与所有行动集均为有限的有限阶段模型中，定义函数()nV i *，使其满足如下等式：()()()()()⎥⎦⎤⎢⎣⎡+=∑∈+∈S j n i A a nj V a i j p a i r i V 1**,,max()()()()()∑∈++=Sj n n n j V i f i j p i f i r 1***,, ……..(5.1)()0,...,2,1,,--=∈N N N n S i 其中()01*=+j V N 。

则由上述算式求出的()()()()00001,2,...,V V V V l ****=即为有限阶段模型的最优值函数，即对每个i S ∈，均有()()0sup ,N V i V i ππ*∈∏=；与此同时求得的决策序列()01,,...,N f f f π****=即为最优策略，其中{1,2,...,}S l =。

由于所有的()(),A i i S∈及{1,2,...,}S l =均为有限集，故由(5.1)式求得的()n f i *一定存在，且达到最优的行动可能多于一个（此时可任取一个作为()n f i *）。

定理5.1不仅解决了有限阶段模型求解最优策略的方法问题，而且还表明对任何n ，()i V n*表示在阶段n ，从状态i 出发，在余下1N n +-的阶段的最优期望总报酬，()1,,...,n n N f f f ***+也构成从n 到阶段N 的最优策略，这体现了Bellman 的最优化原理。

马尔可夫模型实例python全文共四篇示例，供读者参考第一篇示例：马尔可夫模型是一种统计学模型，用于描述一个系统在连续时间之间的状态转移概率。

它基于马尔可夫过程，即未来状态仅仅取决于当前状态，与过去状态无关。

马尔可夫模型在自然语言处理、金融市场预测、天气预测等领域有着广泛的应用。

在这篇文章中，我们将使用Python来实现一个简单的马尔可夫模型实例。

我们将从头开始构建一个简单的文本生成模型，以便展示马尔可夫模型如何工作。

我们需要定义一个包含文本数据的样本数据集。

在这个例子中，我们将使用莎士比亚的《罗密欧与朱丽叶》作为我们的文本数据集。

我们将读取文本文件，并将其转换为一个字符串。

```pythonwith open('romeo_and_juliet.txt', 'r') as file:text = file.read().replace('\n', ' ')```接下来，我们需要预处理我们的文本数据，以便于后续的分析。

我们将使用nltk库来进行文本分词和清洗。

```pythonimport nltknltk.download('punkt')from nltk.tokenize import word_tokenize然后，我们可以构建我们的马尔可夫模型。

我们将创建一个字典，其中键值对为当前单词和下一个单词的组合。

这样我们就可以根据当前单词来预测下一个单词。

```pythondef build_markov_model(tokens):markov_model = {}for i in range(len(tokens) - 1):current_word = tokens[i]next_word = tokens[i + 1]return markov_modelreturn text通过运行上述代码，我们就可以生成一个基于马尔可夫模型的文本。

马尔可夫决策过程算法（原创版）目录一、马尔可夫决策过程算法概述二、马尔可夫决策过程算法的基本概念1.四元组（S, A, P, R）2.状态值函数的贝尔曼方程3.最优状态值函数的贝尔曼最优性方程三、马尔可夫决策过程算法的求解方法1.动态规划2.蒙特卡洛方法3.时序差分学习四、马尔可夫决策过程算法在实际应用中的案例五、总结正文一、马尔可夫决策过程算法概述马尔可夫决策过程（Markov Decision Process，简称 MDP）是强化学习中的一个重要概念，它是一种数学模型，用于描述决策者在不确定环境中进行决策的过程。

MDP 具有广泛的应用，包括资源分配、生产调度、金融投资、机器人控制等。

在本文中，我们将详细介绍马尔可夫决策过程的基本概念、性质、求解方法以及实际应用。

二、马尔可夫决策过程算法的基本概念1.四元组（S, A, P, R）在马尔可夫决策过程中，决策者（Agent）在每个时刻根据当前状态选择一个行动，并根据状态转移概率转移到下一个状态，同时获得一个即时奖励。

决策者的目标是选择一组行动序列（策略），使得累积奖励最大化。

马尔可夫决策过程可以表示为一个四元组（S, A, P, R），其中：- S：状态（State）- A：行动（Action）- P：状态转移概率（Transition Probability）- R：奖励（Reward）2.状态值函数的贝尔曼方程状态值函数（State-Value Function）表示在某个状态下，遵循某个策略能够获得的期望回报。

状态值函数的贝尔曼方程（Bellman Equation）用于计算状态值函数。

3.最优状态值函数的贝尔曼最优性方程最优状态值函数（Optimal State-Value Function）表示在每个状态下，遵循最优策略能够获得的期望回报。

最优状态值函数的贝尔曼最优性方程（Bellman Optimality Equation）用于计算最优状态值函数。

条件马尔可夫模型条件马尔可夫模型（Conditional Markov Model）是一种用于建模序列数据的概率模型。

它是马尔可夫模型的一种扩展，通过考虑当前状态和前一个状态之间的条件关系，能够更准确地预测未来的状态。

在条件马尔可夫模型中，序列数据被看作是由一系列离散的状态组成的。

每个状态可以是一个观察值或者隐藏状态，隐藏状态是指在模型中不能直接观测到的状态，而观察值则是可以直接观测到的状态。

条件马尔可夫模型假设每个状态的出现仅依赖于前一个状态，这被称为马尔可夫性质。

在实际应用中，条件马尔可夫模型被广泛应用于自然语言处理、语音识别、机器翻译等领域。

例如，在自然语言处理中，可以使用条件马尔可夫模型来预测下一个单词出现的概率，从而实现语言模型的建模。

在语音识别中，可以使用条件马尔可夫模型来对语音信号进行建模，从而实现语音识别的任务。

条件马尔可夫模型可以分为两类：隐马尔可夫模型（Hidden Markov Model，HMM）和条件随机场（Conditional Random Field，CRF）。

隐马尔可夫模型是最常用的条件马尔可夫模型之一，它假设隐藏状态和观察值之间存在一个概率关系，并通过学习这个关系来对未知的状态进行预测。

隐马尔可夫模型包括三个基本问题：状态序列问题、观测序列问题和学习问题。

状态序列问题是给定观测序列，求解最可能的状态序列；观测序列问题是给定状态序列，求解观测序列的概率；学习问题是根据观测序列和对应的状态序列，估计模型参数。

条件随机场是另一种常用的条件马尔可夫模型，它是一种无向图模型，用于建模标注问题。

与隐马尔可夫模型不同的是，条件随机场考虑了观测值之间的相关性，可以更好地建模序列数据之间的依赖关系。

条件随机场包括两个基本问题：标注问题和学习问题。

标注问题是给定观测序列，求解最可能的状态序列；学习问题是根据观测序列和对应的状态序列，估计模型参数。

无论是隐马尔可夫模型还是条件随机场，它们都是一种重要的序列建模工具，可以用于处理各种实际问题。