(完整版)解直角三角形超经典例题讲解

解直角三角形典型题型解析一、仰角：指的是向上看时，视线与水平线的夹角。

视线在水平线以上时,在视线所在的垂直平面内,视线与水平线所成的角叫做仰角。

俯角指的是向下看时，视线与水平线的夹角。

1：在竖直面内的水平线与向下递降线段之间的角度(朝下看时，视线与水平面夹角为俯角) 2：从测量员的仪器到照准点所观测到的地平线以下的垂直角3：俯角范围0到180°4：视线在水平线以下时，在视线所在的垂直平面内，视线与水平线所成的角也叫俯角。

视角，视线与显示器等的垂直方向所成的角度，观察物体时，从物体两端（上、下或左、右）引出的光线在人眼光心处所成的夹角。

物体的尺寸越小，离观察者越远，则视角越小。

正常眼能区分物体上的两个点的最小视角约为1分。

坡度与坡角教案二、坡面的铅直高度h和水平宽度的比叫做坡度（或叫做坡比），一般用i表示。

即ｉ＝，常写成i=1：m的形式如i=1:2.5。

把坡面与水平面的夹角α叫做坡角．坡度i与坡角α之间具有什么关系？坡面水平宽度一定，铅直高度与坡度有何关系如图，铅直高度AB一定，水平宽度BC增加，α将变小，坡度减小，因为tan ＝，AB不变，tan 随BC增大而减小；当水平宽度BC不变，α将随铅直高度增大而增大，tanα也随之增大，因为tan = 不变时，tan 随AB的增大而增大教师点拨：一艘海轮位于灯塔P的北偏东65 方向，距离灯塔80海里的A处，它沿正南方向航行一段时间后，到达位于灯塔P的南偏东34 方向上的B处.这时，海轮所在的B处距离灯塔P有多远？水库大坝的横断面是梯形，坝顶宽6m，坝高23m，斜坡AB的坡度i=1∶3，斜坡CD的坡度i=1∶2.5，求斜坡AB的坡面角α，坝底宽AD和斜坡AB的长(精确到0.1m)练习：(1)一段坡面的坡角为60°，则坡度i=______；______，坡角______度．2、利用土埂修筑一条渠道，在埂中间挖去深为0.6米的一块(图阴影部分是挖去部分)，已知渠道内坡度为1∶1.5，渠道底面宽BC为0.5米，求：①横断面(等腰梯形)ABCD的面积；②修一条长为100米的渠道要挖去的土方数．习题：1.一段铁路路基的横断面是等腰三角形,路基顶宽为9.8米,路基高为5.8米,斜坡的坡度i=1:1.6.求坡角.(精确到1°)计算路基下底宽度的长;(精确导0.1米)解: 作BE⊥AD,CF⊥AD,垂足分别为E,F.由题意,可知BE=5.8米,AE=FD,EF=BC=9.8米.在Rt△ABE 中,∵i=BE/AE=1/1.6,∴AE=.6BE=1.6×5.8=9.28AD=AE+EF+FD=2AE+EF=2×9.28+9.8≈28.4(米).设坡角为a,则i=tga=1/1.6,∴a≈32°.答:路基下底宽度为28.4米,坡角为32°.2.在△ABC中，∠C=90度，a、b、c分别为∠A、∠B、∠C的对边，a+b=2,∠B =60度，则c=（0解：a+b=2,a=b√3（√3+1）a=2 a=2/(√3+1)c=4/(√3+1)=2(√3-1)3.如图，小岛A在港口P的南偏西45°方向上，一艘船从港口P沿正南方向以每小时12海里的速度航行，1小时30分后到达B处，在B处测得小岛A在它的南偏西60°的方向上，小岛A离港口P有多少海里（精确到0.1海里）？解：延长pb至c，使pc⊥ac ∵南偏西45°∴PAC为等腰直角三角形ac=pc pb=12*1.5=18设bc=x，因为南偏西60°，所以ac=pc=（根3）x 则x+18=（根3）x x=9（根3+1）ac=9（3+根3）AP=根2*ac=根2*9（3+根3）=1.414*9*（3+1.732）=60.2海里4.航行中的船，在A处看到它的南偏东30°方向上有一灯塔C，船以每小时30海里速度向东南方向航行，半小时后，到达B处，看到灯塔C在船的正西方向，则这时船与灯塔的距离BC=_____海里解1：AB=30*0.5=15 得AE=BE=15*二分之根号二（45度）EC=AE*三分之根号三（30度）BC=BE-CE解2：设原来船就在S点，船向南行驶半小时也就是30*（1/2）=15海里后到达C点此时C在A点正西方，所以三角形ASC是直角三角形∠S=30°船航行的距离SC=30*（1/2）=15（海里）∴AC=SC*tanS=5√3（海里）即船与灯塔的距离是5√3海里5.在高楼前点测得楼顶的仰角为，向高楼前进60米到点，又测得仰角为，则该高楼的高度大约为（）解：设楼顶点为A，楼底点为B，前进60米后到点C，因∠ABC=90°,∠ACB=45°,∠ADB=30°,所以AB=BC=1/2AD，再设楼高为H，即AB=BC=H，则AD=2H，BD=BC+CD=H+60由勾股定理，△ABD中，AB²+BD²=AD²即H²+(H+60)²=(2H)²解这个方程即可得H=60/（√3-1）6.一只船自西向东航行，上午9时到一座灯塔的西南68海里，上午11时到达这座灯塔的正南，求这只船的速度. 解：A、B为船，C为灯塔因为船自西向东航行，A在C的西南方，B在C的正南方所以角A=角C=45度，即三角形ABC为等腰直角三角形设AB、BC为x 所以x的平方+x的平方=68的平方解得x约等于48 因为从A到B经过了2小时（11-9=2）所以速度=48/2=247.某大草原上有一条笔直的公路，在紧靠公路相距40千米的A，B两地，分别有甲，乙两个医疗站，如图，在A 地北偏东45°，B地北偏西60°方向上有一牧民区C．一天，甲医疗队接到牧民区的求救电话，立刻设计了两种救助方案．方案I：从A地开车沿公路到离牧民区C最近的D处，再开车穿越草地沿DC方向到牧民区C．方案II：从A地开车穿越草地沿AC方向到牧民区C．已知汽车在公路上行驶的速度是在草地上行驶速度的3倍．（1）求牧民区到公路的最短距离CD；（2）你认为甲医疗队设计的两种救助方案，哪一种方案比较合理？并说明理由．（结果精确到0.1，参考数据：根号3取1.73，根号2取1.41）解：因为AB=40，依题可得AD=CD，可设AD为x，则CD=x，DB=40-x；I、又因为角CBD=30度；所以CD/BD=tan30所以可得x/（40-x）=1.73/3，所以计算可得x=14.7 所以CD=14.7II、设汽车在草地上行驶的速度为一个单位，则汽车在公路上行驶的速度为3个单位；依上题可计算AC=20.7，所以方案II从AC走的时间为20.7而方案I从AD,CD方向走的时间为2*14.7/3=9.8可以看到20.7远远大于9.8，即从方案II走所用的时间远远方案I所以选择方案I比较合理8.有两条公路ON,OM相交成30°，沿公路OM方向80米处于一所小学，当拖拉机沿ON方向行驶时，路两旁50米处的范围内会受到噪声的影响，已知拖拉机的速度为18km/h，那么拖拉机沿ON方向行驶将给小学带来噪音影响的时间有多长？解：既然路两旁50米处的范围内会受到噪声的影响，那么只要求出第一次距学校50m的那个点（设其为A）到第二次距学校50m的那个点（设其为B）之间的距离AB，再除以拖拉机一秒走多远（18km/h太大了，化为5米/秒）。

解直角三角形经典题型应用题1. 一个田径运动员越过一根高度为2米的木板，如果他离地面的水平距离是3米，那么他的起跳点距离木板底部的高度是多少？解：设起跳点距离木板底部的高度为x，则根据勾股定理，得到：$x^2 + 3^2 = 2^2$化简得：$x^2 = 2^2 - 3^2 = -5$由于x是高度，因此应该为正数。

但是由于方程无解，因此无法解出起跳点距离木板底部的高度。

这个结果告诉我们，如果要跨越一个木板，距离不能太远，否则就无法起跳！2. 一个人看到一个高楼，测得距离为50米，角度为30度，那么这个高楼的高度是多少？解：设高楼的高度为h，根据三角函数，得到：$tan(30) = \frac{h}{50}$化简得：$h = 50\times tan(30) = 50 \times \frac{1}{\sqrt{3}} \approx28.87$因此，这个高楼的高度约为28.87米。

3. 一个人站在一座桥上，看到一条河流在他的正下方流过，测得桥与河面的垂直距离为20米，角度为45度，那么河宽是多少？解：设河宽为w，根据三角函数，得到：$tan(45) = \frac{w}{20}$化简得：$w = 20\times tan(45) = 20$因此，河宽为20米。

4. 在一个矩形田地中，角A的顶点和角B的底点均在田地边界上，角A的角度为30度，角B的角度为60度，且田地的长宽比为3:2，那么田地的面积是多少？解：假设田地的长为3x，宽为2x，则田地的面积为6x²。

又根据三角函数，得到：$tan(30) = \frac{3x}{y}$$tan(60) = \frac{2x}{y}$化简得：$x = y\times tan(30) = y\cdot\frac{1}{\sqrt{3}}$ $x = y\times tan(60) = y\cdot\sqrt{3}$解得：$y = 6\sqrt{3}$因此，田地的面积为6x² = 1080平方米。

专题05 解直角三角形【考点1：锐角三角函数的定义】 【考点2：锐角三角函数的增减性】【考点3：同角三角函数的关系】 【考点4：互余两角三角函数的关系】【考点5：特殊角的三角函数值】 【考点6：解直角三角形】【考点7：解直角三角形的应用】 【考点8：解直角三角形的应用-坡度坡角】【考点9：解直角三角形的应用-仰角俯角】 【考点10：解直角三角形的应用-方向角问】知识点1:锐角三角函数的概念如图所示，在Rt △ABC 中，∠C ＝90°，∠A 所对的边BC 记为a ，叫做∠A 的对边，也叫做∠B 的邻边，∠B 所对的边AC 记为b ，叫做∠B 的对边，也是∠A 的邻边，直角C 所对的边AB 记为c ，叫做斜边．锐角A 的对边与斜边的比叫做∠A 的正弦，记作sinA ，即sin A aA c Ð==的对边斜边；锐角A 的邻边与斜边的比叫做∠A 的余弦，记作cosA ，即cos A bA c Ð==的邻边斜边；锐角A 的对边与邻边的比叫做∠A 的正切，记作tanA ，即tan A aA A bÐ==Ð的对边的邻边.同理sin B b B c Ð==的对边斜边；cos B a B c Ð==的邻边斜边；tan B b B B aÐ==Ð的对边的邻边．ACa b知识点2:锐角三角函数的增减性（1）在0°－90°之间，锐角的正弦值随角度的增大而增大；（2）在0°－90°之间，锐角的余弦值随角度的增大而减小；（3）在0°－90°之间，锐角的正切值随角度的增大而增大.知识点3:特殊角的三角函数值　利用三角函数的定义，可求出30°、45°、60°角的各三角函数值，归纳如下：锐角30°45°160°知识点4:解直角三角形　在直角三角形中，由已知元素(直角除外)求未知元素的过程，叫做解直角三角形. 在直角三角形中，除直角外，一共有5个元素，即三条边和两个锐角. 设在Rt△ABC中，∠C=90°，∠A、∠B、∠C所对的边分别为a、b、c，则有： ①三边之间的关系：a2+b2=c2(勾股定理). ②锐角之间的关系：∠A+∠B=90°. ③边角之间的关系： ，，， ，，. ④，h为斜边上的高.知识点5 ：解直角三角形的常见类型及解法已知条件解法步骤两直角边(a ，b)由求∠A ，∠B=90°－∠A ，两边斜边，一直角边(如c ，a)由求∠A ，∠B=90°－∠A ，锐角、邻边(如∠A ，b)∠B=90°－∠A ，，一直角边和一锐角锐角、对边(如∠A ，a)∠B=90°－∠A ，，Rt △ABC一边一角斜边、锐角(如c ，∠A)∠B=90°－∠A ，，知识点6：解直角三角形的应用解直角三角形的知识应用很广泛，关键是把实际问题转化为数学模型，善于将某些实际问题中的数量关系化归为直角三角形中的边角关系是解决实际应用问题的关键.解这类问题的一般过程是：(1)弄清题中名词、术语的意义，如仰角、俯角、坡度、坡角、方向角等概念，然后根据题意画出几何图形，建立数学模型.(2)将已知条件转化为几何图形中的边、角或它们之间的关系，把实际问题转化为解直角三角形的问题.(3)根据直角三角形(或通过作垂线构造直角三角形)元素(边、角)之间的关系解有关的直角三角形.(4)得出数学问题的答案并检验答案是否符合实际意义，得出实际问题的解.知识点7：解直角三角形的应用-坡度坡角　在用直角三角形知识解决实际问题时，经常会用到以下概念：　(1)坡角：坡面与水平面的夹角叫做坡角，用字母表示.　坡度(坡比)：坡面的铅直高度h和水平距离的比叫做坡度，用字母表示，则，如图，坡度通常写成=∶的形式.知识点8: 解直角三角形应用-仰角俯角问题　仰角、俯角：视线与水平线所成的角中，视线中水平线上方的叫做仰角，在水平线下方的叫做俯角，如图.知识点9：解直角三角形应用-方位角问题（1）方位角：从某点的指北方向线按顺时针转到目标方向的水平角叫做方位角，如图①中，目标方向PA，PB，PC的方位角分别为是40°，135°，245°.(2)方向角：指北或指南方向线与目标方向线所成的小于90°的水平角，叫做方向角，如图②中的目标方向线OA，OB，OC，OD的方向角分别表示北偏东30°，南偏东45°，南偏西80°，北偏西60°.特别如：东南方向指的是南偏东45°，东北方向指的是北偏东45°，西南方向指的是南偏西45°，西北方向指的是北偏西45°.注意：1．解直角三角形实际是用三角知识，通过数值计算，去求出图形中的某些边的长或角的大小，最好画出它的示意图.2．非直接解直角三角形的问题，要观察图形特点，恰当引辅助线，使其转化为直角三角形或矩形来解. 　3．解直角三角形的应用题时，首先弄清题意(关键弄清其中名词术语的意义)，然后正确画出示意图，进而根据条件选择合适的方法求解.【考点1：锐角三角函数的定义】1．（2022秋•儋州期末）在Rt△ABC中，∠C＝90°，AB＝6，BC＝3，cos A的值是（ ）A．B．C．D．【答案】B【解答】解：∵在Rt△ABC中，∠C＝90°，AB＝6，BC＝3，∴，∴．故选：B．2．（2022秋•凤阳县期末）Rt△ABC中，∠C＝90°，cos A＝，AC＝6cm，那么BC等于（ ）A．8cm B．cm C．cm D．cm【答案】A【解答】解：∵在Rt△ABC中，∠C＝90°，cos A＝＝，AC＝6cm，∴AB＝10cm，∴BC＝＝8cm．故选：A．3．（2016秋•长宁区期末）在△ABC中，∠C＝90°，AB＝5，BC＝4，那么∠A的正弦值是（ ）A．B．C．D．【答案】D【解答】解：∵∠C＝90°，AB＝5，BC＝4，∴sin A＝＝，故选：D．4．（2022秋•保德县校级期末）如图，将△ABC放在每个小正方形的边长为1的网格中，点A，B，C均在格点上，则tan C的值是（ ）A．2B．C．1D．【答案】B【解答】解：如图在Rt△ACD中，tan C＝，故选：B．5．（2022秋•桃江县期末）如图，在Rt△ABC中，∠ACB＝90°，CD⊥AB于D，下列式子正确的是（ ）A．sin A＝B．cos A＝C．tan A＝D．cos B＝【答案】A【解答】解：∵∠ACB＝90°，CD⊥AB，∴∠A+∠DCA＝90°，∠DCA+∠BCD＝90°，∴∠A＝∠BCD，∴sin A＝sin∠BCD＝，故选：A．【考点2：锐角三角函数的增减性】6．（2022秋•静安区期末）如果0°＜∠A＜60°，那么sin A与cos A的差（ ）A．大于0B．小于0C．等于0D．不能确定【答案】D【解答】解：当0°＜∠A＜45°时，45°＜90°﹣∠A＜90°，∴sin A＜sin（90°﹣A），∴sin A＜cos A，∴sin A﹣cos A＜0，当∠A＝45°时，90°﹣∠A＝45°，∴sin A＝sin（90°﹣A），∴sin A＝cos A，∴sin A﹣cos A＝0，当45°＜∠A＜60°时，30°＜90°﹣∠A＜45°，∴sin A＞sin（90°﹣A），∴sin A＞cos A，∴sin A﹣cos A＞0，∴当0°＜∠A＜60°时，那么sin A与cos A的差不能确定．故选：D．7．（2022秋•路北区校级期末）如图所示，是由小正方形构成的4×4网格，每个小正方形的顶点叫做格点，点O，A，P，C，D均在格点上，则∠AOB和∠COD的大小关系为（ ）A．∠AOB＞∠COD B．∠AOB＝∠COD C．∠AOB＜∠COD D．无法确定【答案】C【解答】解：如图，连接AP，过点A作AN⊥OP于N，∴OP＝＝，OD＝＝，S △OPA ＝S 梯形OPFE ﹣S △AOE ﹣S △PAF＝×（1+2）×2﹣×2×1﹣×1×1＝3﹣1﹣＝，又∵S △OPA ＝××AN ，即××AN ＝，∴AN ＝，∴sin ∠AOB ＝＝＝0.6，∵sin ∠COD ＝＝≈0.7，∵0.6＜0.7，即sin ∠AOB ＜sin ∠COD ，∴∠AOB ＜∠COD ，故选：C ．【考点3：同角三角函数的关系】8．（2022秋•西安期末）在Rt △ABC 中，∠C ＝90°，BC ＝3，，则tan A ＝（ ）A ．B ．C ．D ．【答案】A【解答】解：在Rt △ABC 中，∠C ＝90°，BC ＝3，，∴AB ＝＝＝5，∴AC ＝＝＝4，∴tan A ＝＝，9．（2022秋•兴化市期末）在△ABC中，∠C＝90°，tan A＝2，则sin A的值为（ ）A．B．C．D．2【答案】B【解答】解：如图：∵∠C＝90°，∴tan A＝＝2，设AC＝x，则BC＝2x，∴AB＝＝x，∴sin A＝＝＝．故选：B．10．（2017秋•道里区期末）在Rt△ABC中，∠C＝90°，sin A＝，则cos A的值等于（ ）A．B．C．D．【答案】B【解答】解：∵sin A＝sin A＝，∴可设a＝3，c＝5，由勾股定理可求得b＝4，∴cos A＝＝，故选：B【考点4：互余两角三角函数的关系】11．（2023秋•九台区期末）在Rt△ABC中，∠C＝90°，sin B＝，则tan A的值为（ ）A．B．C．2D．【解答】解：∵∠C＝90°，sin B＝，∴设AC＝x，AB＝3x，则BC＝2x，则tan A＝＝＝2．故选：C．12．（2022秋•池州期末）在Rt△ACB中，∠C＝90°，，则sin B的值为（ ）A．B．C．D．【答案】A【解答】解：设Rt△ACB中，∠C＝90°，∠A、∠B、∠C的对边分别为a、b、c，由于tan A＝＝2，可设a＝2k，b＝k，由勾股定理得，c＝＝5k，∴sin B＝＝，故选：A．13．（2022秋•太康县期末）在三角形ABC中，∠C为直角，sin A＝，则tan B的值为（ ）A．B．C．D．【答案】A【解答】解：△ABC中，∠C＝90°，则∠A+∠B＝90°，cos B＝sin A＝．sin B＝＝，tan B＝＝＝，故选：A．14．（2022秋•泰山区期末）如图，在Rt△ABC中，∠C＝90°，tan A＝2，则sin B＝（ ）A．B．2C．D．【答案】C【解答】解：∵∠C＝90°，tan A＝2，∴BC＝2AC，∴，∴，故C正确．故选：C．【考点5：特殊角的三角函数值】15．（2022秋•密云区期末）∠A为锐角，若cos A＝，则∠A的度数为（ ）A．75°B．60°C．45°D．30°【答案】B【解答】解：∵∠A为锐角，cos A＝，∴∠A＝60°．故选：B．16．（2022秋•古冶区期末）计算的值（ ）A．0B．C．1D．【答案】C【解答】解：，故C正确．故选：C．17．（2021秋•慈利县期末）在△ABC中，若|sin A﹣|+（﹣cos B）2＝0，则∠C的度数是（ ）A．45°B．75°C．105°D．120°【答案】C【解答】解：由题意得，sin A﹣＝0，﹣cos B＝0，即sin A＝，＝cos B，解得，∠A＝30°，∠B＝45°，∴∠C＝180°﹣∠A﹣∠B＝105°，故选：C．18．（2022秋•东平县校级期末）已知α为锐角，且sin（α﹣10°）＝，则α等于（ ）A．45°B．55°C．60°D．65°【答案】B【解答】解：∵sin45°＝，∴α﹣10°＝45°，解得，α＝55°，故选：B．【考点6：解直角三角形】19．（2022秋•金安区校级期末）如图，∠B＝60°，AB＝4，AC＝6，则cos C的值是（ ）A．B．C．D．【答案】D【解答】解：过A作AD⊥BC，垂足是D，在Rt△ABD中，∠B＝60°，∴∠BAD＝30°，∴BD＝2，AD＝，在Rt△ADC中，CD＝，∴cos C＝＝故选：D．28．（2023春•广州期末）如图，在△ABC中，AD⊥BC于点D，AD＝2，BD＝1，DC＝4，求∠BAC的度数．【答案】90°．【解答】解：∵AD＝2，BD＝1，DC＝4，∴，∵∠BDA＝∠ADC＝90°，∴△BDA∽△ADC，∴∠BAD＝∠C，∵∠C+∠DAC＝90°，∴∠BAD+∠DAC＝90°，∴∠BAC＝90°26．（2022秋•徐汇区期末）如图，已知在△ABC中，CD⊥AB，垂足为点D，AD＝2，BD＝6，tan B＝，点E是边BC的中点．（1）求边AC的长；（2）求∠EAB的正弦值．【答案】（1）2；（2）．【解答】解：（1）∵CD⊥AB，∴△ACD、△BCD均为直角三角形．在Rt△CDB中，∵BD＝6，tan B＝＝，∴CD＝4．在Rt△CDA中，AC＝＝＝2．（2）过点E作EF⊥AB，垂足为F．∵CD⊥AB，EF⊥AB，∴CD∥EF．又∵点E是边BC的中点，∴EF是△BCD的中位线．∴DF＝BF＝3，EF＝CD＝2．∴AF＝AD+DF＝5．在Rt△AEF中，AE＝＝＝．∴sin∠EAB＝＝＝．27．（2022秋•黄浦区校级期末）如图，在Rt△ABC中，∠CAB＝90°，sin C＝，AC＝8，BD平分∠CBA交AC边于点D．求：（1）线段AB的长；（2）tan∠DBA的值．【答案】见试题解答内容【解答】解：（1）∵在Rt△ABC中，∠CAB＝90°，∴sin C＝＝，BC2﹣AB2＝AC2，∴可设AB＝3k，则BC＝5k，∵AC＝8，∴（5k）2﹣（3k）2＝82，∴k＝2（负值舍去），∴AB＝3×2＝6；（2）过D点作DE⊥BC于E，设AD＝x，则CD＝8﹣x．∵BD平分∠CBA交AC边于点D，∠CAB＝90°，∴DE＝AD＝x．在Rt△BDE与Rt△BDA中，，∴Rt△BDE≌Rt△BDA（HL），∴BE＝BA＝6，∴CE＝BC﹣BE＝5×2﹣6＝4．在Rt△CDE中，∵∠CED＝90°，∴DE2+CE2＝CD2，∴x2+42＝（8﹣x）2，解得x＝3，∴AD＝3，∴tan∠DBA＝＝＝．【考点7：解直角三角形的应用】20．（2022秋•丛台区校级期末）如图，AC是电杆AB的一根拉线，测得BC＝6米，∠ACB ＝52°，则拉线AC的长为（ ）A．米B．米C．米D．6⋅cos52°米【答案】C【解答】解：∵cos∠ACB＝＝＝cos52°，∴AC＝米．故选：C．21．（2022秋•岱岳区校级期末）如图，小明为了测量门口一棵大树的高度，他自制一个Rt△DEF纸板测量大树AB的高度，已知tan∠EDF＝0.5，他调整自己的位置，设法使斜边DF 保持水平，并且边DE与点B在同一直线上，测得边DF离地面的高度AC＝1.5m，CD＝13m，则树AB的高度是（ ）A．7m B．7.5m C．8m D．8.5m【答案】C【解答】解：由题意，得：∠DCB＝90°，tan∠EDF＝0.5，CD＝13m，∴BC＝CD⋅tan∠EDF＝13×0.5＝6.5m，∴AB＝AC+BC＝1.5+6.5＝8m；故选：C．22．（2022秋•南关区校级期末）如图，在天定山滑雪场滑雪，需从山脚下A处乘缆车上山顶B处，缆车索道与水平线所成的∠BAC＝α，若山的高度BC＝800米，则缆车索道AB 的长为（ ）A．800sinα米B．800cosα米C．米D．米【答案】C【解答】解：在Rt△ACB中，∵∠ACB＝90°，sin BAC＝，∴AB＝．∵∠BAC＝α，BC＝800米，∴AB＝（米）．故选：C．23．（2020秋•太和县期末）《九章算术》是我国古代数学成就的杰出代表，其中《方田》章给出计算弧田面积所用公式为：弧田面积＝（弦×矢+矢2），弧田（如图）是由圆弧和其所对的弦所围成，公式中“弦”指圆弧所对弦长AB，“矢”等于半径长与圆心O 到弦的距离之差．在如图所示的弧田中，“弦”为8，“矢”为3，则cos∠OAB＝（ ）A．B．C．D．【答案】B【解答】解：如图，作OH⊥AB于H．由题意：AB＝8，OA﹣OH＝3，∵OH⊥AB，∴AH＝BH＝4，∵AH2+OH2＝OA2，∴42＝（OA+OH）（OA﹣OH），∴OA+OH＝，∴OA＝，OH＝，∴cos∠OAB＝＝＝，故选：B．24．（2022秋•南关区校级期末）在山坡上植树，要求两棵树间的坡面距离是3，测得斜坡的倾斜角为27°，则斜坡上相邻两棵树的水平距离是（ ）A．3sin27°B．3cos27°C．D．3tan27°【答案】B【解答】解：如图，过点A作AB⊥BC于B，∴∠ABC＝90°，cos∠BAC＝，∵AC＝3，∠BAC＝27°，∴AB＝AC cos∠BAC＝3cos27°；故选：B．【考点8：解直角三角形的应用-坡度坡角】25．（2022秋•丛台区校级期末）河堤横断面如图所示，堤高BC＝6米，迎水坡AB的坡比为1：，则AB的长为（ ）A．12米B．米C．米D．米【答案】A【解答】解：Rt△ABC中，BC＝6米，＝1：，∴AC＝BC×＝6（米），∴AB＝＝＝12（米）．故选：A．29．（2023秋•宽城区期末）某风景区观景缆车路线如图所示，缆车从点A出发，途经点B 后到达山顶P，其中AB＝400米，BP＝200米，且AB段的运行路线与水平方向的夹角为15°，BP段的运行路线与水平方向的夹角为30°，求垂直高度PC．（结果精确到1米，参考数据：sin15°≈0.259，cos15°≈0.966，tan15°≈0.268）【答案】垂直高度PC约为204米．【解答】解：过点B作BD⊥PC，垂足为D，过点B作BE⊥AC，垂足为E，由题意得：CD＝BE，在Rt△ABE中，∠A＝15°，AB＝400米，∴BE＝AB•sin15°≈400×0.259＝103.6（米），∴CD＝BE＝103.6米，在Rt△BDP中，∠PBD＝30°，BP＝200米，∴DP＝BP＝100（米），∴PC＝PD+DC≈204（米），∴垂直高度PC约为204米．30．（2022秋•平乡县期末）如图是某货站传送货物的平面示意图．为了提高传送过程的安全性，工人师傅欲减小传送带与地面的夹角，使其由45°改为30°，已知原传送带AB 长为4米．（1）求新传送带AC的长度；（2）如果需要在货物着地点C的左侧留出2米的通道，试判断距离B点5米的货物MNQP是否需要挪走，并说明理由．（参考数据：≈1.4，≈1.7．）【答案】见试题解答内容【解答】解：（1）如图，在Rt△ABD中，∠ABD＝45°，∴AD＝BD，∴2AD2＝AB2＝（4）2，解得：AD＝4（米）．在Rt△ACD中，∵∠ACD＝30°，∴AC＝2AD＝8（米）．即新传送带AC的长度约为8米；（2）货物MNQP不需要挪走．理由：在Rt△ABD中，BD＝AD＝4（米）．在Rt△ACD中，CD＝＝4（m）．∴CB＝CD﹣BD＝4﹣4≈2.8（m）．∵PC＝PB﹣CB≈5﹣2.8＝2.2＞2，∴货物MNQP不需要挪走．【考点9：解直角三角形的应用-仰角俯角】31．（2023秋•沈河区期末）无人机在实际生活中的应用越来越广泛．如图所示，某人利用无人机测量教学楼的高度BC，无人机在空中点P处，测得点P距地面上A点30米，点A处的俯角为55°，距楼顶C点10米，点C处的俯角为30°，其中点A，B，C，P在同一平面内，若每层教学楼的高度为3.5米，楼顶加盖2米，求该教学楼的层数．（结果保留整数，参考数据：sin55°≈0.82，cos55°≈0.57，tan55°≈1.4）【答案】5层．【解答】解：过点P作PD⊥AB于点D，过点C作CE⊥PD于点E，则∠PAB＝55°，PA＝30米，PC＝10米，∠PCE＝30°，BC＝DE，在Rt△PAD中，sin55°＝≈0.82，解得PD≈24.6，在Rt△PCE中，sin30°＝＝，解得PE＝5，∴DE＝PD﹣PE＝19.6米，∴BC＝19.6米，设该教学楼的层数为m层，由题意得，3.5m+2＝19.6，解得m≈5，∴该教学楼的层数为5层．32．（2022秋•定远县期末）如图大楼AB的高度为37m，小可为了测量大楼顶部旗杆AC的高度，他从大楼底部B处出发，沿水平地面前行32m到达D处，再沿着斜坡DE走20m 到达E处，测得旗杆顶端C的仰角为30°．已知斜坡ED与水平面的夹角∠EDG＝37°，图中点A，B，C，D，E，G在同一平面内（结果精确到0.1m）（1）求斜坡ED的铅直高度EG和水平宽度GD．（2）求旗杆的AC高度．（参考数据：sin37°≈0.60，cos37°≈0.80，tan37°≈0.75，≈1.73）【答案】（1）斜坡ED的铅直高度EG约为12m，水平宽度GD约为16m；（2）旗杆的AC高度约为2.7m．【解答】解：（1）在Rt△DEG中，∠EDG＝37°，DE＝20m，∴EG＝DE•sin37°≈20×0.60＝12（m），DG＝DE•cos37°≈20×0.80＝16（m），∴斜坡ED的铅直高度EG约为12m，水平宽度GD约为16m；（2）过点E作EH⊥BC，垂足为H，由题意得：DB＝32m，∴EH＝GB＝GD+DB＝16+32＝48（m），在Rt△CEH中，∠CEH＝30°，∴CH＝EH•tan30°＝48×＝16（m），∴AC＝CH+BH﹣AB＝16+12﹣37≈2.7（m），∴旗杆的AC高度约为2.7m．33．（2022秋•舞钢市期末）已知：如图，斜坡AP的坡度为1：2.4，坡长AP为39米，在坡顶A处的同一水平面上有一座古塔BC，在斜坡底P处测得该塔的塔顶B的仰角为45°，在坡顶A处测得该塔的塔顶B的仰角为76°．求：（1）坡顶A到地面PQ的距离；（2）古塔BC的高度（结果精确到1米）．（参考数据：sin76°≈0.97，cos76°≈0.24，tan76°≈4.01）【答案】（1）15米．（2）28米．【解答】解：（1）过点A作AH⊥PQ，垂足为点H，∵斜坡AP的坡度为1：2.4，∴，设AH＝5a米，则PH＝12a米，由勾股定理得，AP＝＝13a（米），∴13a＝39，解得a＝3，∴AH＝15米．答：坡顶A到地面PQ的距离为15米．（2）延长BC交PQ于点D，由题意得，CD＝AH＝15米，AC＝DH，∵∠BPD＝45°，∴PD＝BD．设BC＝x米，则BD＝PD＝（x+15）米，由（1）可得PH＝12×3＝36（米），∴AC＝HD＝PD﹣PH＝x+15﹣36＝（x﹣21）米，在Rt△ABC中，tan76°＝≈4.01，解得x≈28，经检验，x≈28是原方程的解且符合题意．∴古塔BC的高度约为28米．34．（2022秋•金水区期末）嵩岳寺塔，位于登封市区西北5公里嵩山南麓峻极峰下嵩岳寺内，是嵩岳寺内唯一的北魏遗存建筑，也是中国现存最古老的砖塔，它见证了这座寺院的千年历史．小明想知道塔的高度．于是走到点C处，测得此时塔尖A的仰角是37°，向前走了11.8米至点F处，测得此时塔尖A的仰角是45°，已知小明的眼睛离地面高度是1.6米，请你帮他求出嵩岳寺塔AB的高度．（参考数据：sin37°≈，cos37°≈，tan37°≈）【答案】嵩岳寺塔AB的高度约为37米．【解答】解：由题意得：∠DCB＝∠FEB＝∠GBE＝∠BGD＝90°，CD∥EF∥AB，则四边形DCFE、四边形FEGB、四边形DCBG均为矩形，∴BG＝EF＝CD＝1.6米，CF＝DE＝11.8米，在Rt△AGE中，∠AEG＝45°，∴△AGE是等腰直角三角形，∴AG＝EG，设AG＝EG＝x米，则DG＝（x+11.8）米，在Rt△AGD中，tan∠ADG＝＝tan37°≈，即≈，解得：x≈35.4，经检验，x≈35.4是原方程的解，且符合题意，∴AG≈35.4米，∴AB＝AG+BG≈35.4+1.6＝37（米），答：嵩岳寺塔AB的高度约为37米．【考点10：解直角三角形的应用-方向角问】35．（2023春•兴城市期末）如图，某天上午海岸瞭望塔C接到位于其北偏西60°方向且相距12海里的渔船A的求救信号，于是立即通知处在瞭望塔正西方向B处的北斗救援队前往救援，救援队测得船A位于B的东北方向，求此时救援队与渔船之间的距离AB．（结果保留根号）【答案】救援队与渔船之间的距离AB为6海里．【解答】解：如图，过点A作AD⊥BC于点D，则∠ADB＝∠ADC＝90°，由题意可知，AC＝12海里，∠ABD＝45°，∠ACE＝60°，∴△ABD是等腰直角三角形，∠ACD＝90°﹣∠ACE＝90°﹣60°＝30°，∴AD＝BD，AD＝AC＝×12＝6（海里），∴AB＝＝AD＝×6＝6（海里），答：救援队与渔船之间的距离AB为6海里．36．（2022秋•安岳县期末）如图，A、B两地是我国某海域一东西方向上的两个小岛．一天，一艘渔政船在C处巡逻时，测得小岛A在它的北偏东15°方向上，它沿西北方向航行海里后到达D处，测得小岛A在它的东北方向．（1）求D处与小岛A的距离；（2）若该渔政船在D处测得小岛B在它的北偏西53°方向上，求小岛A、B之间的距离．（参考数据：sin53°＝，cos53°＝，tan53°＝）【答案】（1）海里；（2）70海里．【解答】解：（1）由题意，得∠ADC＝90°，∠ACD＝60°，∴tan60°＝，∵海里，∴海里．答：D处与小岛A的距离为海里；（2）过点D作DE⊥AB于点E．由题意得：∠ADE＝45°，∠BDE＝53°，∵海里，∴DE＝AE＝30海里，在Rt△BDE中，tan53°＝＝，∴BE＝×30＝40（海里），∴AB＝40+30＝70（海里）．答：小岛A、B之间的距离为70海里．37．（2022秋•渝中区校级期末）如图，一艘渔船以每小时30海里的速度自东向西航行，在B处测得补给站C在北偏西30°方向，继续航行2小时后到达A处，测得补给站C在北偏东60°方向．（1）求此时渔船与补给站C的距离；（结果保留根号）（2）此时渔船发现在A点北偏西15°方向的D点处有大量鱼群，渔船联系了补给站，决定调整方向以原速前往作业，与此同时补给站C测得点D在北偏西75°方向，并立即派出补给船给渔船补给食物和淡水，若两船恰好在D处相遇，求补给船的速度．（精确到十分位，参考数据：≈1.41，≈1.73，≈2.45）．【答案】（1）此时渔船与补给站C的距离为30海里；（2）补给船的速度约为41.0海里/时．【解答】解：（1）由题意得：AB＝30×2＝60（海里），∠CAB＝90°﹣60°＝30°，∠CBA＝90°﹣30°＝60°，∴∠ACB＝180°﹣∠CAB﹣∠CBA＝90°，在Rt△ACB中，AC＝AB•sin n60°＝60×＝30（海里），∴此时渔船与补给站C的距离为30海里；（2）如图：过点A作AE⊥CD，垂足为E，∴∠AEC＝∠AED＝90°，由题意得：∠DAC＝15°+60°＝75°，FA∥CG，∴∠ACG＝∠FAC＝60°，∴∠ACD＝180°﹣75°﹣60°＝45°，∴∠EAC＝90°﹣∠ACD＝45°，∴∠DAE＝∠DAC﹣∠EAC＝30°，在Rt△AEC中，AC＝30海里，∴AE＝AC•sin45°＝30×＝15（海里），CE＝AC•cos45°＝30×＝15（海里），在Rt△ADE中，DE＝AE•tan30°＝15×＝15（海里），∴AD＝2DE＝30（海里），∴DC＝DE+CE＝（15+15）海里，∴＝＝（小时），∴补给船的速度＝＝＝15+15≈41.0（海里/时），∴补给船的速度约为41.0海里/时．一．选择题（共9小题）1．（2023秋•铁西区期末）如图，在Rt△ABC中，∠ACB＝90°，BC＝1，AB＝3，则下列结论正确的是（ ）A．B．C．cos B＝3D．【答案】D【解答】解：∵∠ACB＝90°，BC＝1，AB＝3，∴AC＝＝＝2，A．sin A＝＝，故A选项错误；B．tan A＝＝＝，故B选项错误；C．cos B＝＝，故C选项错误；D．tan B＝＝2，故D选项正确；故选：D．2．（2023秋•于洪区期末）如图，在△ABC中，∠C＝90°，AC＝1，BC＝2，则cos A的值为（ ）A．B．2C．D．【答案】C【解答】解：在Rt△ACB中，∠C＝90°，AC＝1，BC＝2，∴AB＝＝＝，∴cos A＝＝＝，故选：C．3．（2022秋•海口期末）如图，某地入口处原有三级台阶，每级台阶高为20cm，深为30 cm，拟将台阶改为斜坡，设台阶的起点为A，斜坡的起始点为C，现设计斜坡的坡度i＝1：5，则AC的长度是（ ）A．200cm B．210cm C．240cm D．300cm【答案】C【解答】解：过B作BD⊥AC，由题可知BD＝60cm，AD＝60cm．∵tan∠BCA＝＝，∴DC＝300cm，∴AC＝DC﹣AD＝300﹣60＝240（cm）．故选：C．4．（2022秋•赫山区期末）如图，在平面直角坐标系xOy中，点P（4，3），OP与x轴正半轴的夹角为α，则sinα的值为（ ）A．B．C．D．【答案】A【解答】解：过P作PN⊥x轴于N，PM⊥y轴于M，则∠PMO＝∠PNO＝90°，∵点P（4，3），∴ON＝PM＝4，PN＝3，，∴，故选：A．5．（2022秋•市中区期末）若锐角α满足，则＝（ ）A．B．C．D．【答案】C【解答】解：∵，∴α＝60°，∴，故选：C．6．（2022秋•高青县期末）如图，小王在高台上的点A处测得塔底点C的俯角为α，塔顶点D的仰角为β，已知塔的水平距离AB＝a，则此时塔高CD的长为（ ）A．a sinα+a sinβB．a tanα+a tanβC．D．【答案】B【解答】解：∵AB＝a，AB⊥CD，在Rt△ABD中有，BD＝AB•tanβ＝a tanβ，在Rt△ABC中有，BC＝AB•tanα＝a tanα，∴CD＝BD+BC＝a tanβ+a tanα．故选：B．7．（2022秋•石家庄期末）如图，小明为了测量遵义市湘江河的对岸边上B，C两点间的距离，在河的岸边与BC平行的直线EF上点A处测得∠EAB＝37°，∠FAC＝60°，已知河宽18米，则B，C两点间的距离为（ ）（参考数据：sin37°，cos37°≈，tan37°≈）A．（18+6）米B．（24+10）米C．（24+6）米D．（24+18）米【答案】C【解答】解：作AD⊥BC于点D，如图，∵BC∥EF，∴∠DBA＝∠EAB，∠DCA＝∠CAF，∵∠EAB＝37°，∠CAF＝60°，∴∠DBA＝37°，∠DCA＝60°，∵AD＝18米，tan∠DBA＝，tan∠DCA＝，∴＝，＝，解得BD＝24米，CD＝6米，∴BC＝BD+CD＝（24+6）米，故选：C．8．（2021秋•泗水县期末）如图，在Rt△ABC中，CD是斜边AB上的高，∠A≠45°，则下列比值中不等于cos B的是（ ）A．B．C．D．【答案】C【解答】解：A．∵CD⊥AB，∴∠CDB＝∠ADB＝90°，∴∠B+∠BCD＝90°，∵∠ACB＝90°，∴∠ACD+∠BCD＝90°，∴∠B＝∠ACD，在Rt△ACD中，cos∠ACD＝，∴cos B＝，故A不符合题意；B．在Rt△DBC中，cos B＝，故B不符合题意；C．在Rt△DBC中，cos∠BCD＝，∵∠A≠45°，∴∠B≠45°，∴∠B≠∠BCD，∴cos B≠，故C符合题意；D．在Rt△ABC中，cos B＝，故D不符合题意；故选：C．9．（2022秋•安化县期末）某兴趣小组想测量一座大楼AB的高度．如图，大楼前有一段斜坡BC，已知BC的长为12米，它的坡度i＝1：．在离C点40米的D处，用测量仪测得大楼顶端A的仰角为37度，测角仪DE的高度为1.5米，求大楼AB的高度约为（ ）米．（sin37°＝0.60，cos37°＝0.80，tan37°＝0.75，＝1.73）A．39.3B．37.8C．33.3D．25.7【答案】C【解答】解：如图，延长AB交直线DC于点F，过点E作EH⊥AF，垂足为点H．在Rt△BCF中，BF：CF＝1：，设BF＝k米，则CF＝k米，∴BC＝＝2k（米），又∵BC＝12米，∴2k＝12，∴k＝6，∴BF＝6米，CF＝6米，∵DF＝DC+CF，∴DF＝（40+6）米，在Rt△AEH中，tan∠AEH＝，∴AH＝tan37°×（40+6）≈37.785（米），∵BH＝BF﹣FH，∴BH＝6﹣1.5＝4.5（米）．∵AB＝AH﹣HB，∴AB＝37.785﹣4.5≈33.3（米）．即大楼AB的高度约为33.3米．故选：C．二．填空题（共6小题）10．（2023秋•和平区期末）2023年9月29日开通沈阳地铁四号线，如图是某站地铁扶梯的示意图，扶梯AB的坡度i＝5：12（i为铅直高度与水平宽度的比）．小明乘扶梯从扶梯底端A以0.5米/秒的速度用时39秒到达扶梯顶端B，则小明上升的铅直高度BC为　7.5　米．【答案】7.5．【解答】解：由题意知AB＝39×0.5＝19.5（米），∵扶梯AB的坡度i＝5：12，∴，设BC＝5k米，AC＝12k米，则（米），∴，∴BC＝5×1.5＝7.5（米），故答案为：7.5．11．（2022秋•新市区校级期末）如图，一条船上午8时从海岛A出发，以15海里/时的速度向正北方向航行，上午10时到达海岛B处，分别从A，B处望灯塔C，测得∠NAC＝30°，∠NBC＝60°．若这条船继续向正北航行，再航行　15　海里，小船与灯塔C的距离最短．【答案】15．【解答】解：∵一条船上午8时从海岛A出发，以15海里/时的速度向正北方向航行，上午10时到达海岛B处，∴AB＝15×2＝30（海里），∵∠NBC＝60°，∠NAC＝30°，∴∠ACB＝30°，∴BC＝AB＝30（海里），如图，过点C作CP⊥AB于点P．∴根据垂线段最短，线段CP的长为小船与灯塔C的最短距离，∠BPC＝90°．又∵∠NBC＝60°，∴∠PCB＝180°﹣∠BPC﹣∠CBP＝30°．在Rt△CBP中，∠BCP＝30°，∴（海里），∴再航行15海里，小船与灯塔C的距离最短．故答案为：15．12．（2022秋•定远县期末）如图，B、C是河岸边两点，A是对岸岸边一点，测得∠ABC＝45°，∠ACB＝45°，BC＝60 m，则点A到对岸BC的距离是　30　m．【答案】见试题解答内容【解答】解：由题意可得：∠A＝180°﹣45°﹣45°＝90°，AB＝AC＝BC×sin45°＝30．∵面积S＝AB×AC＝BC×h，∴h＝30．故点A到对岸BC的距离是30米．13．（2022秋•定远县期末）如图，某船由西向东航行，在点A测得小岛O在北偏东60°方向上，船航行了10海里后到达点B，这时测得小岛O在北偏东45°方向上，船继续航行到点C时，测得小岛O恰好在船的正北方，则此时船到小岛的距离为 海里．【答案】．【解答】解：设OC＝x海里，依题意得，∠OAC＝30°，∠OBC＝45°，∴BC＝OC＝x海里，海里．∵AB＝AC﹣BC，∴AC﹣BC＝10海里，即，∴，答：此时船到小岛的距离为5（+1）海里；故答案为：．14．（2022秋•灵宝市期末）如图，某游客在山脚下乘览车上山．导游告知，索道与水平线成角∠BAC为40°，览车速度为60米/分，11分钟到达山顶，请根据以上信息计算山的高度BC约为　422　米．（精确到1米）（参考数据：sin40°≈0.64，cos40°≈0.77，tan40°≈0.84）【答案】422．【解答】解：由题意可知，AB＝60×11＝660，在Rt△ABC中，∠ACB＝90°，∵sin∠BAC＝sin40°＝，∴BC＝660×0.64＝422.4≈422（米），答：山的高度BC约为422米．故答案为：422．15．（2022秋•芝罘区期末）如图，某活动小组利用无人机航拍校园，已知无人机的飞行速度为4m/s，从A处沿水平方向飞行至B处需10s，若在地面C处测得A处的仰角为75°，B处的仰角为30°，则这架无人机的飞行高度大约是　27m　．（结果精确到1m，参考数据；，）【答案】27m．【解答】解：如图，过点A作AD⊥BC于点D，过点B作水平线的垂线，垂足为点E，由题意得：AB＝4×10＝40（m），∠ACE＝75°，∠BCE＝30°，AB∥CE，∴∠ACB＝∠ACE﹣∠BCE＝45°，∠ABC＝∠BCE＝30°，在Rt△ABD中，，，在Rt△ACD中，，∴，在Rt△BCE中，，即这架无人机的飞行高度大约是27m，故答案为：27m．三．解答题（共4小题）16．（2022秋•尧都区期末）为庆祝中国共产党第二十次全国代表大会的胜利召开，某校准备通过热气球升到楼顶来悬挂宣传标语．如图，有一热气球到达离地面高度为36米的A处时，仪器显示正前方一高楼顶部B的仰角是37°，底部C的俯角是60°，为了安全到达楼顶，气球应至少再上升多少米？（结果精确到0.1米）（参考数据：sin37°≈0.60，cos37°≈0.80，tan37°≈0.75，）【答案】15.6米．【解答】解：如图，过点A作AD⊥BC于D，在Rt△ADC中，CD＝36米，∠CAD＝60°，∵tan∠CAD＝，∴AD＝＝＝12≈20.76（米），在Rt△ADB中，∠BAD＝37°，则BD＝AD•tan∠BAD≈20.76×0.75≈15.6（米），答：气球应至少再上升15.6米．17．（2022秋•儋州期末）如图，为了测量我校某教学楼AB的高，数学兴趣小组的甲同学在C处看到楼顶A的仰角为45°，同时乙同学在斜坡CD上的D处看见楼顶A的仰角为30°．若斜坡CD的坡比i＝1：2，铅锤高度DG＝4米（点B、C、G在同一水平线上）．求：（1）CG＝　8　米，∠CAD＝　15　度；（2）教学楼AB的高（参考数据：，结果精确到个位）．【答案】（1）8，15；（2）20.4米．【解答】解：（1）如图，作DH⊥AB于点H，∵斜坡CD的坡比i＝1：2，铅锤高度DG＝4米，∴GC＝2DG＝8．由题意知∠ADH＝30°，∠ACB＝45°，∴∠DAH＝60°，∠CAB＝45°，∴∠CAD＝∠DAH﹣∠CAB＝15°，故答案为：8，15；（2）设AB＝x m，∵∠CAB＝∠ACB＝45°，∴BC＝AB＝x m，∵DH⊥AB，DG⊥BG，HB⊥GB，∴四边形DGBH是矩形，∴DH＝BG＝GC+CB＝8+x，HB＝DG＝4，∴AH＝AB﹣HB＝x﹣4，∵∠ADH＝30°，∴，即，解得，即教学楼AB的高为20.4米．18．（2022秋•保德县校级期末）某数学活动小组到山西省台怀镇开展综合性实践活动，准备测量中国现存最高藏式古塔的高度．如图，藏式古塔DE在高54m的小山EC上，在A 处测得古塔底部E处的仰角为31°，再沿AC方向前进22m到达B处，测得古塔顶部D 处的仰角为60°，且点C，B，A在同一条水平线上，求藏式古塔DE的高度．（结果精确到1m；参考数据：sin31°≈0.52，cos31°≈0.86，tan31°≈0.60，）【答案】64m．【解答】解：由题意可得，EC＝54m，AB＝22m，∠DBC＝60°，∠EAC＝31°，设DE＝x m，则DC＝（x+54）m，在Rt△DCB中，∵tan∠DBC＝，即，∴，在Rt△ECA中，，∴，由题意得，，解得，x≈64，答：塑像DE的高度约为64m．19．（2020秋•市南区校级期末）如图，某高楼顶部有一信号发射塔，在矩形建筑物ABCD 的A、C两点处测得该塔顶端F的仰角分别为∠α＝48°，∠β＝65°，矩形建筑物宽度AD＝20m，高度DC＝35m．计算该信号发射塔顶端到地面的高度FG（结果精确到1m）．（参考数据：sin48°≈0.7，cos48°≈0.7，tan48°≈1.1，sin65°≈0.9，cos65°≈0.4，tan65°≈2.1）【答案】该信号发射塔顶端到地面的高度FG为120m．【解答】解：延长AD交FG于H，则四边形ABGH是矩形，AB＝CD＝GH＝30m，AH＝BG．设FH＝x m．在RtAFH中，AH＝＝，∴CG＝DH＝﹣20，在Rt△FCG中，tan65°＝，∴2.1＝，∴x＝84.7，∴FG＝FH+GH＝84.7+35＝119.7≈120（m），答：该信号发射塔顶端到地面的高度FG为120m．。

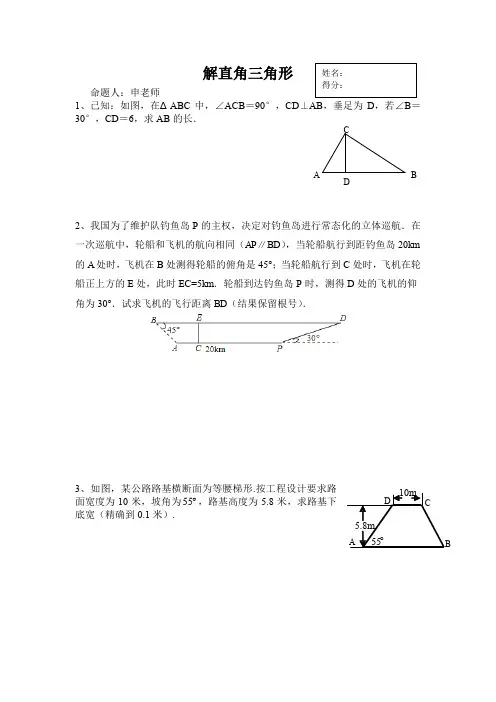
解直角三角形命题人：申老师1、已知：如图，在ΔABC 中，∠ACB ＝90°，CD ⊥AB ，垂足为D ，若∠B ＝30°，CD ＝6，求AB 的长．2、我国为了维护队钓鱼岛P 的主权，决定对钓鱼岛进行常态化的立体巡航．在一次巡航中，轮船和飞机的航向相同（AP ∥BD ），当轮船航行到距钓鱼岛20km 的A 处时，飞机在B 处测得轮船的俯角是45°；当轮船航行到C 处时，飞机在轮船正上方的E 处，此时EC =5km ．轮船到达钓鱼岛P 时，测得D 处的飞机的仰角为30°．试求飞机的飞行距离BD （结果保留根号）．3、如图，某公路路基横断面为等腰梯形.按工程设计要求路面宽度为10米，坡角为︒55，路基高度为5.8米，求路基下底宽（精确到0.1米）.C AD B4、为申办2010年冬奥会，须改变哈尔滨市的交通状况。

在大直街拓宽工程中，要伐掉一棵树AB ，在地面上事先划定以B 为圆心，半径与AB 等长的圆形危险区，现在某工人站在离B 点3米远的D 处，从C 点测得树的顶端A 点的仰角为60°，树的底部B 点的俯角为30°.问：距离B 点8米远的保护物是否在危险区内？5、如图，某一水库大坝的横断面是梯形ABCD ，坝顶宽CD ＝5米，斜坡AD ＝16米，坝高 6米，斜坡BC 的坡度3:1=i .求斜坡AD 的坡角∠A （精确到1分）和坝底宽AB ．（精确到0.1米）6. 在一次实践活动中，某课题学习小组用测倾器、皮尺测量旗杆的高度，他们设计了如下的方案（如图1所示）：（1） 在测点A 处安置测倾器，测得旗杆顶部M 的仰角∠MCE ＝α ； （2） 量出测点A 到旗杆底部N 的水平距离AN ＝m; （3） 量出测倾器的高度AC ＝h 。

根据上述测量数据，即可求出旗杆的高度MN 。

如果测量工具不变，请参照上述过程，重新设计一个方案测量某小山高度（如图2）1）在图2中，画出你测量小山高度MN 的示意图2）写出你的设计方案。

2024年新课标中考数学二轮必考抢分专练解直角三角形及其应用1如图，小兵同学从A处出发向正东方向走x米到达B处，再向正北方向走到C处，已知∠BAC=α，则A，C两处相距()A.xsinα米 B.xcosα米 C.x⋅sinα米 D.x⋅cosα米【答案】B【解析】根据锐角三角函数中余弦值的定义即可求出答案.小兵同学从A处出发向正东方向走x米到达B处，再向正北方向走到C处，∴∠ABC=90°，AB=x米.∴cosα=ABAC，∴AC=ABcosα=xcosα米.故选：B .【点睛】本题考查了锐角三角函数中的余弦值，解题的关键在于熟练掌握余弦值的定义.余弦值就是在直角三角形中，锐角的邻边与斜边之比.2日照灯塔是日照海滨港口城市的标志性建筑之一，主要为日照近海及进出日照港的船舶提供导航服务．数学小组的同学要测量灯塔的高度，如图所示，在点B处测得灯塔最高点A的仰角∠ABD=45°，再沿BD方向前进至C处测得最高点A的仰角∠ACD=60°，BC=15.3m，则灯塔的高度AD大约是() (结果精确到1m，参考数据：2≈1.41，3≈1.73)A.31mB.36mC.42mD.53m【答案】B【解析】在Rt△ADB中，得出AD=BD，设AD=x，则BD=x，CD=x-15.3，在Rt△ADC中，根据正切得出tan∠ACD=ADCD=xx-15.3=3，求解即可得出答案．【详解】在Rt△ADB中，∠ABD=45°，∴AD=BD，设AD=x，则BD=x，CD=x-15.3，在Rt△ADC中，∠ACD=60°，∴tan∠ACD=ADCD =xx-15.3=3，∴x≈36，∴灯塔的高度AD大约是36m．故选：B．【点睛】本题考查了解直角三角形中的仰俯角问题，解题的关键是弄清有关的直角三角形中的有关角的度数．3如图，某商场有一自动扶梯，其倾斜角为28°，高为7米．用计算器求AB的长，下列按键顺序正确的是()A. B.C. D.【答案】B【解析】根据正弦的定义得出AB=7÷sin28°，进而可得答案．由题意得sin28°=7 AB，∴AB=7÷sin28°，∴按键顺序为7 ÷ sin2 8 = ，故选：B．【点睛】本题考查了正弦的定义，计算器的使用，正确理解三角函数的定义是解题的关键．4一渔船在海上A处测得灯塔C在它的北偏东60°方向，渔船向正东方向航行12海里到达点B处，测得灯塔C在它的北偏东45°方向，若渔船继续向正东方向航行，则渔船与灯塔C的最短距离是海里．【答案】63+6##6+63【解析】过点C作CD⊥AB交于点D，利用特殊角的三角函数值，列方程即可解答．如图，过点C 作CD ⊥AB 交于点D ，由题意可知tan ∠CAD =tan30°=33,tan ∠CBD =tan45°=1，设CD 为x ，∴BD =CD ÷tan45°=x ，AD =CD ÷tan30°=3x ，根据AB =AD -BD ，可得方程3x -x =12，解得x =63+6，∴渔船与灯塔C 的最短距离是63+6 海里，故答案为：63+6．【点睛】考查了解解直角三角形-方位角问题，熟知特殊角度的三角函数值是解题的关键．5如图，焊接一个钢架，包括底角为37°的等腰三角形外框和3m 高的支柱，则共需钢材约m (结果取整数)．(参考数据：sin37°≈0.60，cos37°≈0.80，tan37°≈0.75)【答案】21【解析】根据解直角三角形及等腰三角形的性质可进行求解．∵△ABC 是等腰三角形，且CD ⊥AB ，∴AD =BD ，∵CD =3m ，∴AC =BC =CD sin37°=5m ,AD =BD =CD tan37°=4m ，∴共需钢材约为2AC +2AD +CD =21m ；故答案为21．【点睛】本题主要考查解直角三角形，熟练掌握三角函数是解题的关键．6如图，将45°的∠AOB 按下面的方式放置在一把刻度尺上：顶点O 与尺下沿的端点重合，OA 与尺下沿重合，OB 与尺上沿的交点B 在尺上的读数恰为2cm ，若按相同的方式将22.5°的∠AOC 放置在该刻度尺上，则OC 与尺上沿的交点C 在尺上的读数为cm ．【答案】22+2【解析】根据平行线的性质得到∠DBO=∠AOB=45°，解直角三角形求出OB=22cm，再推出∠BOC=∠BCO，进而得到BC=BO=22cm，再求出CD的长即可得到答案．由题意得，BC∥OA，∠BDO=90°，OB=2cm，∴∠DBO=∠AOB=45°，∴OB=BD=22cmcos∠DBO∵∠AOC=22.5°，∴∠BOC=∠AOB-∠AOC=22.5°，∠BCO=∠AOC=22.5°，∴∠BOC=∠BCO，∴BC=BO=22cm，∴CD=BD+BC=22+2cm，∴OC与尺上沿的交点C在尺上的读数为22+2cm，故答案为：22+2．【点睛】本题主要考查了解直角三角形，平行线的性质，等腰三角形的判定，正确求出BC的长是解题的关键．7如图，O,R是同一水平线上的两点，无人机从O点竖直上升到A点时，测得A到R点的距离为40m,R点的俯角为24.2°，无人机继续竖直上升到B点，测得R点的俯角为36.9°．求无人机从A点到B点的上升高度AB(精确到0.1m)．参考数据：sin24.2°≈0.41,cos24.2°≈0.91,tan24.2°≈0.45，sin36.9°≈0.60,cos36.9°≈0.80,tan36.9°≈0.75．【答案】无人机从A点到B点的上升高度AB约为10.9米【解析】解Rt△AOR，求得AO，OR，在Rt△BOR中，求得BO，根据AB=BO-AO，即可求解．依题意，∠ARO=24.2°，∠BRO=36.9°，AR=40，在Rt△AOR中，∠ARO=24.2°，∴AO=AR×sin∠ARO=40×sin24.2°，RO=AR×cos∠ARO=40×cos24.2°，在Rt△BOR中，OB=OR×tan∠BRO=40×cos24.2°×tan36.9°，∴AB=BO-AO=40×cos24.2°×tan36.9°-40×sin24.2°≈40×0.91×0.75-40×0.41≈10.9(米)答：无人机从A点到B点的上升高度AB约为10.9米．【点睛】本题考查了解直角三角形的应用，熟练掌握三角函数的定义是解题的关键．8某风景区观景缆车路线如图所示，缆车从点A出发，途经点B后到达山顶P，其中AB=400米，BP=200米，且AB段的运行路线与水平方向的夹角为15°，BP段的运行路线与水平方向的夹角为30°，求垂直高度PC．(结果精确到1米，参考数据：sin15°≈0.259，cos15°≈0.966，tan15°≈0.268)【答案】垂直高度PC约为204米【解析】【分析】过点B作BD⊥PC于D，作BE⊥AC于E，则四边形DCEB为矩形，在Rt△ABE中利用正弦函数求出DC长度，在Rt△PBD中，∠PBD=30°，可以求出PD长度，即可求出PC．【详解】过点B作BD⊥PC于D，作BE⊥AC于E，则四边形DCEB为矩形，∴DC=BE，在Rt△ABE中，∠A=15°，sin A=BE AB，则BE=AB⋅sin A≈400×0.259=103.6(米)，∴DC=BE=103.6米，在Rt△PBD中，∠PBD=30°，BP=200米，则PD=12BP=100米，∴PC=PD+DC=100+103.6≈204米．答：垂直高度PC约为204米．9钓鱼岛及其附属岛屿是中国的固有领土，神圣不可侵犯！自2021年2月1日起，旨在维护国家主权、更好履行海警机构职责的《中华人民共和国海警法》正式实施．中国海警在钓鱼岛海域开展巡航执法活动，是中方依法维护主权的正当举措．如图是钓鱼岛其中一个岛礁，若某测量船在海面上的点D处测得与斜坡AC坡脚点C的距离为140米，测得岛礁顶端A的仰角为30.96°，以及该斜坡AC的坡度i=5 6，求该岛礁的高(即点A到海平面的铅垂高度)．(结果保留整数)(参考数据：sin30.96°≈0.51，cos30.96°≈0.85，tan30.96°≈0.60)【答案】该岛礁的高AB 为300米．【解析】根据斜坡AC 的坡度i =56，可设AB =5x 米，BC =6x 米，继而表示出BD 的长度，再由tan30.96°≈0.60，可得关于x 的方程，解出即可得出答案．【详解】∵斜坡AC 的坡度i =56，∴AB ：BC =5：6，故可设AB =5x 米，BC =6x 米，在Rt △ADB 中，∠D =30.96°，BD =(140+6x )米，∴tan30.96°=5x 140+6x=0.60，解得：x =60(米)，经检验，x =60是方程的解，∴5x =300(米)，答：该岛礁的高AB 为300米．【点睛】本题考查了解直角三角形的实际应用，构建直角三角形是解题的关键．102023年5月30日9点31分，“神舟十六号”载人飞船在中国酒泉卫星发射中心点火发射，成功把景海鹏、桂海潮、朱杨柱三名航天员送入到中国空间站．如图，在发射的过程中，飞船从地面O 处发射，当飞船到达A 点时，从位于地面C 处的雷达站测得AC 的距离是8km ，仰角为30°；10s 后飞船到达B 处，此时测得仰角为45°．(1)求点A 离地面的高度AO ；(2)求飞船从A 处到B 处的平均速度．(结果精确到0.1km/s ，参考数据：3≈1.73)【答案】(1)4km(2)飞船从A 处到B 处的平均速度约为0.3km/s【解析】【分析】(1)根据含30度角的直角三角形的性质即可得到结论；(2)在Rt △AOC 中，根据直角三角形的性质得到OC =32AC =43km ，在Rt △BOC 中，根据等腰直角三角形的性质得到OB =OC =43km ，于是得到结论．【小问1详解】解：在Rt △AOC 中，∵∠AOC =90°，∠ACO =30°，AC =8km ，∴AO =12AC =12×8=4km ，【小问2详解】在Rt △AOC 中，∵∠AOC =90°，∠ACO =30°，AC =8km ，∴OC =32AC =43km ，在Rt △BOC 中，∵∠BOC =90°，∠BCO =45°，∴∠BCO =∠OBC =45°，∴OB =OC =43km ，∴AB =OB -OA =(43-4)km ，∴飞船从A 处到B 处的平均速度=43-410≈0.3km/s ．【点睛】考查了解直角三角形-俯角仰角问题，准确识图，熟练运用相关知识是解题的关键．11如图，堤坝AB 长为10m ，坡度i 为1:0.75，底端A 在地面上，堤坝与对面的山之间有一深沟，山顶D 处立有高20m 的铁塔CD ．小明欲测量山高DE ，他在A 处看到铁塔顶端C 刚好在视线AB 上，又在坝顶B 处测得塔底D 的仰角α为26°35 ．求堤坝高及山高DE ．(sin26°35 ≈0.45，cos26°35 ≈0.89，tan26°35 ≈0.50，小明身高忽略不计，结果精确到1m )【答案】堤坝高为8米，山高DE 为20米．【解析】过B 作BH ⊥AE 于H ，设BH =4x ，AH =3x ，根据勾股定理得到AB =AH 2+BH 2=5x =10，求得AH =6，BH =8，过B 作BF ⊥CE 于F ，则EF =BH =8，BF =EH ，设DF =a ，解直角三角形即可得到结论．【详解】过B 作BH ⊥AE 于H ，∵坡度i 为1:0.75，∴设BH =4x ，AH =3x ，∴AB =AH 2+BH 2=5x =10，∴x =2，∴AH =6，BH =8，过B 作BF ⊥CE 于F ，则EF =BH =8，BF =EH ，设DF =a ，∵α=26°35 ．∴BF =DF tan26°35=a 0.5=2a ，∴AE =6+2a ，∵坡度i 为1:0.75，∴CE ：AE =20+a +8 ：6+2a =1：0．75，∴a =12，∴DF =12(米)，∴DE =DF +EF =12+8=20(米)，答：堤坝高为8米，山高DE 为20米．【点睛】本题考查了解直角三角形的应用-俯角仰角，解直角三角形的应用-坡角坡度，正确地作出辅助线是解题的关键．12如图1是某红色文化主题公园内的雕塑，将其抽象成加如图2所示的示意图，已知点B ，A ，D ，E 均在同一直线上，AB =AC =AD ，测得∠B =55°，BC =1.8m ，DE =2m ．(结果保小数点后一位)(1)连接CD ，求证：DC ⊥BC ；(2)求雕塑的高(即点E 到直线BC 的距离)．(参考数据：sin55°≈0.82，cos55°≈0.57，tan55°≈1.43)【答案】(1)见解析(2)雕塑的高约为4.2米【解析】【分析】(1)根据等边对等角得出∠B =∠ACB ,∠ACD =∠ADC ，根据三角形内角和定理得出2∠B +∠ADC =180°，进而得出∠BCD =90°，即可得证；(2)过点E 作EF ⊥BC ，交BC 的延长线于点F ，在Rt △BDC 中，得出AD =BC cos B = 1.8cos55°，则BE =AD +DE =2+1.8cos55°，在Rt △EBF 中，根据EF =BE ⋅sin B ，即可求解．【小问1详解】解：∵AB =AC =AD ，∴∠B =∠ACB ,∠ACD =∠ADC∵∠B +∠ADC +∠BCD =180°即2∠B +∠ADC =180°∴∠B +∠ADC =90°即∠BCD =90°∴DC ⊥BC ；【小问2详解】如图所示，过点E 作EF ⊥BC ，交BC 的延长线于点F ，在Rt △BDC 中，∠B =55°，BC =1.8m ，DE =2m∴cos B =BC AD ，∴AD =BC cos B = 1.8cos55°∴BE =AD +DE =2+ 1.8cos55°在Rt △EBF 中，sin B =EF BE，∴EF =BE ⋅sin B×sin55°=2+ 1.8cos55°×0.82≈2+ 1.80.57≈4.2(米)．答：雕塑的高约为4.2米．【点睛】本题考查了等腰三角形的性质，三角形内角和定理的应用，解直角三角形的应用，熟练掌握三角函数的定义是解题的关键．13如图1，是某校教学楼正厅一角处摆放的“教学楼平面示意图”展板，数学学习小组想要测量此展板的最高点到地面的高度．他们绘制了图2所示的展板侧面的截面图，并测得AB=120cm，BD=80cm，∠ABD=105°，∠BDQ=60°，底座四边形EFPQ为矩形，EF=5cm．请帮助该数学学习小组求出展板最高点A到地面PF的距离．(结果精确到1cm．参考数据：2≈1.41，3≈1.73)【答案】159cm【解析】【分析】过点A作AG⊥PF于点G，与直线QE交于点H，过点B作BM⊥AG于点M，过点D作DN⊥BM于点N，分别解作出的直角三角形即可解答．【详解】解：如图，过点A作AG⊥PF于点G，与直线QE交于点H，过点B作BM⊥AG于点M，过点D 作DN⊥BM于点N，∴四边形DHMN，四边形EFGH均为矩形，∴MH=ND，EF=HG=5，BM∥DH，∴∠NBD=∠BDQ=60°，∴∠ABM=∠ABD-∠NBD=105°-60°=45°，在Rt△ABM中，∠AMB=90°，∵sin∠ABM=sin45°=AMAB，=602，∴AM=AB⋅sin45°=120×22在Rt△BDN中，∠BND=90°，∵sin∠NBD=sin60°=NDBD，∴ND=BD⋅sin60°=80×3=403，2∴MH=ND=403，∴AG=AM+MH+GH=602+403+5≈60×1.41+40×1.73+5≈159cm，答：展板最高点A到地面PF的距离为159cm．【点睛】本题考查解直角三角形的应用，正确作出辅助线构造出直角三角形，熟练通过解直角三角形求相应未知量是解题的关键．14如图，l是南北方向的海岸线，码头A与灯塔B相距24千米，海岛C位于码头A北偏东60°方向．一艘勘测船从海岛C沿北偏西30°方向往灯塔B行驶，沿线勘测石油资源，勘测发现位于码头A北偏东15°方向的D处石油资源丰富．若规划修建从D处到海岸线的输油管道，则输油管道的最短长度是多少千米？(结果保留根号)【答案】63-6千米【解析】【分析】过点D作DM⊥AB于点M，由垂线段最短可得DM的长即为所求，先求出∠ACB=90°，再根据等腰直角三角形的判定与性质可得AC=CD，然后在Rt△ABC中，解直角三角形可得AC,BC的长，从而可得BD的长，最后利用含30度角的直角三角形的性质求解即可得．【详解】解：如图，过点D作DM⊥AB于点M，由垂线段最短可知，DM的长即为所求，由题意得：∠BAC=60°,∠BAD=15°,∠BCE=30°,AB∥EF，AB=24千米，∴∠CAD=45°，∠ACF=∠BAC=60°，∠ABC=∠BCE=30°，∴∠ACB=180°-∠ACF-∠BCE=90°，∴Rt△ACD是等腰直角三角形，∴AC =CD ，在Rt △ABC 中，AC =12AB =12千米，BC =AB ⋅cos30°=123千米，∴BD =BC -CD =BC -AC =123-12 千米，在Rt △BDM 中，DM =12BD =63-6 千米，答：输油管道的最短长度是63-6 千米．【点睛】本题考查了解直角三角形的应用、垂线段最短、含30度角的直角三角形的性质，熟练掌握解直角三角形的方法是解题关键．15如图，某育苗基地为了能够最大限度地遮挡夏季炎热的阳光和充分利用冬天的光照，计划在苗圃正上方搭建一个平行于地面的遮阳蓬．已知苗圃的(南北)宽AB =6.5米，该地区一年中正午时刻太阳光与地平面的最大夹角是∠DAE =76.5°，最小夹角是∠DBE =29.5°．求遮阳蓬的宽CD 和到地面的距离CB ．参考数据：sin29.5°≈49100，cos29.5°≈87100，tan29.5°≈1425，sin76.5°≈97100，cos76.5°≈23100，tan76.5°≈215．【答案】CD =7.5米，BC =4.2米．【解析】【分析】过点D 作DF ⊥EB 于F ，解Rt △ADF ，得DF ≈215AF ，解Rt △BDF ，得DF ≈1425AF +6.5 ，所以215AF =1425AF +6.5 ，解得AF =1米，从而得DF =4.2米，再由矩形的性质求解即可．【详解】解：如图，过点D 作DF ⊥EB 于F ，在Rt △ADF 中，∠AFD =90°，∴DF =AF ⋅tan ∠FAD =AF ⋅tan76.5°≈215AF ，在Rt △BDF 中，∠BFD =90°，∴DF =BF ⋅tan ∠FBD =AF +AB ⋅tan29.5°≈1425AF +6.5 ，∴215AF =1425AF +6.5 ，解得：AF =1(米)，∴DF=215×1=4.2(米)，∴BF=AB+AF=6.5+1=7.5(米)，∵∠AFD=ABC=∠C=90°∴矩形BCDF，∴CD=BF=7.5米，BC=DF=4.2米．答：遮阳蓬的宽CD为7.5米，到地面的距离CB为4.2米．【点睛】本题考查解直角三角形的应用，通过作辅助线构造直角三角形是解题的关键．162023年3月，水利部印发《母亲河复苏行动河湖名单(2022-2025年)》，我省境内有汾河、桑干河、洋河、清漳河、浊漳河、沁河六条河流入选．在推进实施母亲河复苏行动中，需要砌筑洛种驳岸(也叫护坡)．某校“综合与实践”小组的同学把“母亲河驳岸的调研与计算”作为一项课题活动，利用课余时间完成了实践调查，并形成了如下活动报告．请根据活动报告计算BC和AB的长度(结果精确到0.1m．参考数据：3≈1.73，2≈1.41)．课题母亲河驳岸的调研与计算调查方式资料查阅、水利部门走访、实地查看了解功能驳岸是用来保护河岸，阻止河岸崩塌或冲刷的构筑物驳岸剖面图相关数据及说明，图中，点A，B，C，D，E在同一竖直平面内，AE与CD均与地面平行，岸墙AB⊥AE于点A，∠BCD=135°，∠EDC= 60°，ED=6m，AE=1.5m，CD=3.5m计算结果交流展示【答案】BC的长约为1.4m,AB的长约为4.2m．【解析】【分析】过点E作EF⊥CD于点F，延长AB,DC交于点H，首先根据∠EDF的三角函数值求出EF =ED⋅sin∠EDF=33，FD=ED⋅cos∠EDF=3，然后得到四边形AEFH是矩形，进而得到CH=HF-CF=1.5-0.5=1，然后在Rt△BCH中利用∠BCH的三角函数值求出BC=CHcos∠BCH =2≈1.4m，进而求解即可．【详解】解：过点E作EF⊥CD于点F，延长AB,DC交于点H，∴∠EFD=90°．由题意得，在Rt△EFD中，∠EDF=60°,ED=6,sin∠EDF=EFED,cos∠EDF=FDED．∴EF=ED⋅sin∠EDF=6×sin60°=6×32=33．∴FD=ED⋅cos∠EDF=6×cos60°=6×12=3．由题意得，∠H=90°，四边形AEFH是矩形．∴AH=EF=33,HF=AE=1.5．∵CF=CD-FD=3.5-3=0.5，∴CH=HF-CF=1.5-0.5=1．∴在Rt△BCH中，∠H=90°,∠BCH=180°-∠BCD=180°-135°=45°．∵cos∠BCH=CHBC ,tan∠BCH=BHCH．∴BC=CHcos∠BCH =1cos45°=122=2≈1.4m．∴BH=CH⋅tan∠BCH=1×tan45°=1，∴AB=AH-BH=33-1≈3×1.73-1≈4.2m．答：BC的长约为1.4m,AB的长约为4.2m．【点睛】本题是解直角三角形的应用，考查了矩形的判定与性质，解直角三角形，关键是理解坡度的含义，构造适当的辅助线便于在直角三角形中求得相关线段．17一天晚上，小明和爸爸带着测角仪和皮尺去公园测量一景观灯(灯杆底部不可到达)的高AB．如图所示，当小明爸爸站在点D处时，他在该景观灯照射下的影子长为DF，测得DF=2.4m；当小明站在爸爸影子的顶端F处时，测得点A的仰角α为26.6°．已知爸爸的身高CD=1.8m，小明眼睛到地面的距离EF=1.6m，点F、D、B在同一条直线上，EF⊥FB，CD⊥FB，AB⊥FB．求该景观灯的高AB．(参考数据：sin26.6°≈0.45，cos26.6°≈0.89，tan26.6°≈0.50)【答案】4.8m【解析】【分析】过点E作EH⊥AB，垂足为H，根据题意可得：EH=FB，EF=BH=1.6m，然后设EH= FB=xm，在Rt△AEH中，利用锐角三角函数的定义求出AH的长，从而求出AB的长，再根据垂直定义可得∠CDF=∠ABF=90°，从而证明A字模型相似三角形△CDF∽△ABF，最后利用相似三角形的性质可得AB=34x，从而列出关于x的方程，进行计算即可解答．【详解】过点E作EH⊥AB，垂足为H，由题意得：EH=FB，EF=BH=1.6m，设EH=FB=xm，在Rt△AEH中，∠AEH=26.6°，∴AH=EH⋅tan26.6°≈0.5x(m)，∴AB=AH+BH=(0.5x+1.6)m，∵CD⊥FB，AB⊥FB，∴∠CDF=∠ABF=90°，∵∠CFD=∠AFB，∴△CDF∽△ABF，∴CD AB =DF BF，∴1.8 AB =2.4x，∴AB=34x，∴34x=0.5x+1.6，解得：x=6.4，∴AB=34x=4.8(m)，∴该景观灯高AB约为4.8m．【点睛】本题考查了解直角三角形的应用-仰角俯角问题，相似三角形的应用，中心投影，根据题目的已知条件并结合图形添加适当的辅助线是解题的关键．18渝昆高速铁路的建成，将会显著提升宜宾的交通地位．渝昆高速铁路宜宾临港长江公铁两用大桥(如图1)，桥面采用国内首创的公铁平层设计．为测量左桥墩底到桥面的距离CD，如图2．在桥面上点A处，测得A到左桥墩D的距离AD=200米，左桥墩所在塔顶B的仰角∠BAD=45°，左桥墩底C的俯角∠CAD=15°，求CD的长度．(结果精确到1米．参考数据：2≈1.41，3≈1.73)【答案】CD的长度54米【解析】【分析】AD上截取AE，使得AE=EC，设CD=x，在Rt△ECD中，ED=3x，EC=2x，则AD= AE+ED=3+2x，进而即可求解．【详解】解：如图所示，AD上截取AE，使得AE=EC，∴∠EAC=∠ECA，∵∠CAD=15°∴∠CED=2∠EAC=30°，设CD=x，在Rt△ECD中，ED=3x，EC=2x∴AD=AE+ED=3+2x又AD=200∴200=3+2x∴x=2003+2=2002-3≈200×2-1.73=54即CD=54米【点睛】本题考查了解直角三角形的应用，熟练掌握三角函数的定义是解题的关键．。

《解直角三角形》典型例题（一）例1 在Rt △ABC 中，∠C=90°，∠B=60°，a=4，解这个三角形．分析 本题实际上是要求∠A 、b 、c 的值．可根据直角三角形中各元素间的关系解决． 解（1）；（2）由a bB =tan ，知；（3）由c a B =cos ，知860cos 4cos =︒==B a c ．说明 此题还可用其他方法求b 和c ．例 2在Rt △ABC 中,∠C=90°，∠A=30°，3=b ,解这个三角形． 解法一 ∵ ∴设 ,则由勾股定理,得∴．∴．解法二133330tan =⨯=︒=b a说明 本题考查含特殊角的直角三角形的解法,它可以用目前所学的解直角三角形的方法,也可以用以前学的性质解题． 例 3设中，于D ，若，解三角形ABC ．分析“解三角形ABC”就是求出的全部未知元素．本题CD不是的边，所以应先从Rt入手．解在Rt中，有：在Rt中，有说明（1）应熟练使用三角函数基本关系式的变形，如：（2）平面几何中有关直角三角形的定理也可以结合使用，本例中“”就是利用“对30°角的直角边等于斜边的一半”这一定理．事实上，还可以用面积公式求出AB的值：所以解直角三角形问题，应开阔思路，运用多种工具．例4在中，，求．分析（1）求三角形的面积一方面可以根据面积公式求出底和底上的高的长，也可以根据其中规则面积的和或差；（2）不是直角三角形，可构造直角三角形求解．解如图所示，作交CB的延长线于H，于是在Rt△ACH中，有，且有；在中，，且，∴；于是，有，则有说明还可以这样求：例5如图，在电线杆上离地面高度5m的C点处引两根拉线固定电线杆，一根拉线AC和地面成60°角，另一根拉线BC和地面成45°角．求两根拉线的总长度（结果用带根号的数的形式表示）．分析分别在两个直角三角形ADC和BDC中，利用正弦函数的定义，求出AC和BC．解:在Rt△ADC中，331023560sin==︒=DCAC在Rt△BDC中，221022545sin==︒=DCBC说明本题考查正弦的定义，对于锐角三角函数的定义，要熟练掌握．。

《解直角三角形》典型例题例1 在Rt △ABC 中，∠C=90°，∠B=60°，a=4，解这个三角形． 分析 本题实际上是要求∠A 、b 、c 的值．可根据直角三角形中各元素间的关系解决． 解 （1） ；（2）由abB =tan ，知 ；（3）由c a B =cos ，知860cos 4cos =︒==B a c ． 说明 此题还可用其他方法求b 和c ．例 2 在Rt △ABC 中, ∠C=90°，∠A=30°，3=b ,解这个三角形．解法一 ∵ ∴设 ,则由勾股定理,得∴ ．∴．解法二 133330tan =⨯=︒=b a说明 本题考查含特殊角的直角三角形的解法,它可以用目前所学的解直角三角形的方法,也可以用以前学的性质解题． 例 3 设 中，于D ，若，解三角形ABC ．分析“解三角形ABC”就是求出的全部未知元素．本题CD不是的边，所以应先从Rt入手．解在Rt中，有：∴在Rt中，有说明（1）应熟练使用三角函数基本关系式的变形，如：（2）平面几何中有关直角三角形的定理也可以结合使用，本例中“”就是利用“对30°角的直角边等于斜边的一半”这一定理．事实上，还可以用面积公式求出AB的值：所以解直角三角形问题，应开阔思路，运用多种工具．例4在中，，求．分析（1）求三角形的面积一方面可以根据面积公式求出底和底上的高的长，也可以根据其中规则面积的和或差；（2）不是直角三角形，可构造直角三角形求解．解如图所示，作交CB的延长线于H，于是在Rt△ACH中，有，且有；在中，，且，∴；于是，有，则有说明还可以这样求：例5 如图，在电线杆上离地面高度5m 的C 点处引两根拉线固定电线杆，一根拉线AC 和地面成60°角，另一根拉线BC 和地面成45°角．求两根拉线的总长度（结果用带根号的数的形式表示）．分析 分别在两个直角三角形ADC 和BDC 中，利用正弦函数的定义，求出AC 和BC ．解: 在Rt △ADC 中，331023560sin ==︒=DC AC 在Rt △BDC 中，221022545sin ==︒=DC BC说明 本题考查正弦的定义，对于锐角三角函数的定义，要熟练掌握．学习要有三心:一信心；二决心；三恒心.知识+方法=能力,能力+勤奋=效率,效率×时间=成绩. 宝剑锋从磨砺出,梅花香自苦寒来.。