5.2 菱形(1)

性质定理1：菱形的四条边都相等。
A
D
B
C
性质定理2：
菱形的两条对角线互相垂直， 每一条对角线平分一D 组对角。
已知:四边形ABCD是菱形 求证:AC⊥BD ，AC平分 A
OC
∠BCA和∠BAD， BD平分
B
∠ABC和∠ADC
证明：∵四边形ABCD是菱形
∴AB=AD (菱形的定义) BO=DO (平行四边形的对角线互相平分)
•不习惯读书进修的人，常会自满于现状，觉得再没有什么事情需要学习，于是他们不进则退。经验丰富的人读书用两只眼睛，一只眼睛看到纸面上的话，另 一眼睛看到纸的背面。2022年3月30日星期三2022/3/302022/3/302022/3/30 •书籍是屹立在时间的汪洋大海中的灯塔。2022年3月2022/3/302022/3/302022/3/303/30/2022 •正确的略读可使人用很少的时间接触大量的文献，并挑选出有意义的部分。2022/3/302022/3/30March 30, 2022 •书籍是屹立在时间的汪洋大海中的灯塔。
实地大演练
轻松过关
1.菱形的两条对角线长分别为6cm
和8cm，则菱形的边长是（C ）
A.10cm B.7cm
D
3
C. 5cm
D.4cm A
4
O
CБайду номын сангаас
B
2.在菱形ABCD中，AE⊥BC，
AF⊥CD，E、F分别为BC，CD的
中点，那么∠EAF的度数是
我 （B ）
A
来 试
A.75°
试 B.60° B
D
C.45° D.30°
B
O
D
E

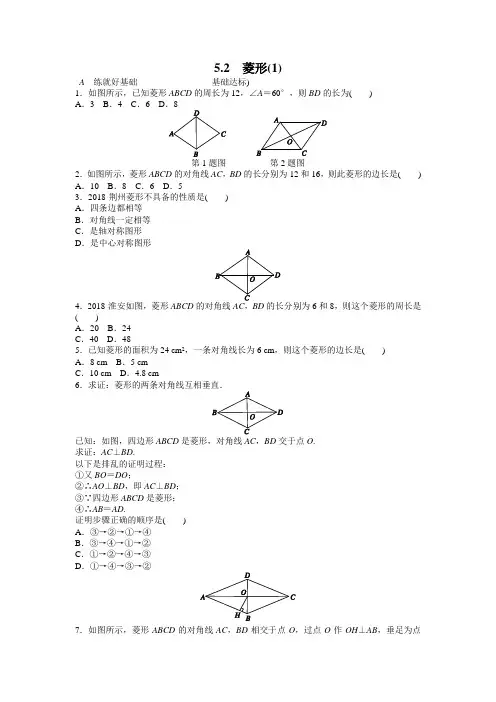
5.2菱形(1)A练就好基础基础达标)1．如图所示，已知菱形ABCD的周长为12，∠A＝60°，则BD的长为()A．3 B．4 C．6 D第1题图第2题图2．如图所示，菱形ABCD的对角线AC，BD的长分别为12和16，则此菱形的边长是() A．10 B．8 C．6 D．53．2018·荆州菱形不具备的性质是()A．四条边都相等B．对角线一定相等C．是轴对称图形D．是中心对称图形4．2018·淮安如图，菱形ABCD的对角线AC，BD的长分别为6和8，则这个菱形的周长是()A．20 B．24C．40 D．485．已知菱形的面积为24 cm2，一条对角线长为6 cm，则这个菱形的边长是()A．8 cm B．5 cmC．10 cm D．4.8 cm6已知：如图，四边形ABCD是菱形，对角线AC，BD交于点O.求证：AC⊥BD.以下是排乱的证明过程：①又BO＝DO；②∴AO⊥BD，即AC⊥BD；③∵四边形ABCD是菱形；④∴AB＝AD.证明步骤正确的顺序是()A．③→②→①→④B．③→④→①→②C．①→②→④→③D．①→④→③→②7．如图所示，菱形ABCD的对角线AC，BD相交于点O，过点O作OH⊥AB，垂足为点H .若AC ＝8，BD ＝6，则点O 到边AB 的距离OH ＝____．8．如图所示，已知菱形ABCD 的一个内角∠BAD ＝80°，对角线AC ，BD 相交于点O ，点E 在AB 上，且BE ＝BO ，则∠8题图9题图9．2018·广州如图，若菱形ABCD 的顶点A ，B 的坐标分别为(3，0)，(－2，0)，点D 在y 轴上，则点C 的坐标是________．10. 如图所示，四边形ABCD 是菱形，DE ⊥AB 交BA 的延长线于点E ，DF ⊥BC 交BC 的延长线于点F . 求证：FC ＝AE .B 更上一层楼 能力提升11．如图所示，小华剪了两条宽为160°，则它们重叠部分的面积为( ) A. 2 B ．1 C.233D ．2 12．四边形ABCD 是菱形，∠BAD ＝60°，AB ＝6，对角线AC 与BD 相交于点O ，点E 在AC 上，若OE ＝3，则CE 的长为____．13．如图所示，四边形ABCD 是菱形，对角线AC ，BD 相交于点O ，DH ⊥AB 于点H ，连结OH ，求证：∠DHO ＝∠DCO .14．如图，在菱形ABCD中，AB＝4，E为BC中点，AE⊥BC于点E，AF⊥CD于点F，CG ∥AE，CG交AF于点H，交AD于点G.(1)求菱形ABCD的面积；(2)求∠CHA的度数．14题图C开拓新思路拓展创新15．如图所示，在菱形ABCD中，∠B＝60°，点E在边BC上，点F在边CD上．(1)如图(a)，若E是BC的中点，∠AEF＝60°，求证：BE＝DF.(2)如图(b)，若∠EAF＝60参考答案5.2菱形(1)A练就好基础基础达标)1．如图所示，已知菱形ABCD的周长为12，∠A＝60°，则BD的长为(A)A．3 B．4 C．6 D第1题图第2题图2．如图所示，菱形ABCD的对角线AC，BD的长分别为12和16，则此菱形的边长是(A) A．10 B．8 C．6 D．53．2018·荆州菱形不具备的性质是(B)A．四条边都相等B．对角线一定相等C．是轴对称图形D．是中心对称图形4．2018·淮安如图，菱形ABCD6和8，则这个菱形的周长是(A)A．20 B．24C．40 D．485．已知菱形的面积为24 cm2，一条对角线长为6 cm，则这个菱形的边长是(B)A．8 cm B．5 cmC．10 cm D．4.8 cm6已知：如图，四边形ABCD是菱形，对角线AC，BD交于点O.求证：AC⊥BD.以下是排乱的证明过程：①又BO＝DO；②∴AO⊥BD，即AC⊥BD；③∵四边形ABCD是菱形；④∴AB＝AD.证明步骤正确的顺序是(B)A．③→②→①→④B．③→④→①→②C．①→②→④→③D．①→④→③→②7．如图所示，菱形ABCD的对角线AC，BD相交于点O，过点O作OH⊥AB，垂足为点H.若AC＝8，BD＝6，则点O到边AB的距离OH＝__2.4__．8．如图所示，已知菱形ABCD的一个内角∠BAD＝80°，对角线AC，BD相交于点O，点E在AB上，且BE＝BO，则∠9题图9．2018·广州如图，若菱形ABCD的顶点A，B的坐标分别为(3，0)，(－2，0)，点D在y 轴上，则点C的坐标是(－5，4)．10. 如图所示，四边形ABCD 是菱形，DE ⊥AB 交BA 的延长线于点E ，DF ⊥BC 交BC 的延长线于点F . 求证：FC ＝AE .证明：连结BD .∵四边形ABCD 是菱形，∴BD 平分∠ABC ，AD ＝CD . 又∵DE ⊥AB ，DF ⊥BC ，∴DE ＝DF . 在Rt △ADE 和Rt △CDF 中， ∵⎩⎪⎨⎪⎧DE ＝DF ，AD ＝CD ，∴Rt △ADE ≌Rt △CDF (HL )， ∴FC ＝AE .B 更上一层楼 能力提升11．如图所示，小华剪了两条宽为160°，则它们重叠部分的面积为( C ) A. 2 B ．1 C.233D ．2 12．四边形ABCD 是菱形，∠BAD ＝60°，AB ＝6，对角线AC 与BD 相交于点O ，点E 在AC 上，若OE ＝3，则CE 的长为． 【解析】∵四边形ABCD 是菱形，∴AB ＝AD ＝6，AC ⊥BD ，OB ＝OD ，OA ＝OC . ∵∠BAD ＝60°，∴△ABD 是等边三角形，∴BD ＝AB ＝6，∴OB ＝12BD ＝3，∴OC ＝OA ＝AB 2－OB 2＝33， ∵点E 在AC 上，OE ＝3，∴CE ＝OC ＋3或CE ＝OC －3， ∴CE ＝43或CE ＝2 3. 故答案为43或2 3.13．如图所示，四边形ABCD 是菱形，对角线AC ，BD 相交于点O ，DH ⊥AB 于点H ，连结OH ，求证：∠DHO ＝∠DCO .证明：∵四边形ABCD 是菱形，∴AB ∥CD ，OD ＝OB ，∠COD ＝90°. ∵DH ⊥AB ，∴OH ＝OB . ∴∠OHB ＝∠OBH .又∵AB ∥CD ，∴∠OBH ＝∠ODC .∴∠OHB ＝∠ODC .∵在Rt △COD 中，∠ODC ＋∠DCO ＝90°， 在Rt △DHB 中，∠DHO ＋∠OHB ＝90°， ∴∠DHO ＝∠DCO .14．如图，在菱形ABCD 中，AB ＝4，E 为BC 中点，AE ⊥BC 于点E ，AF ⊥CD 于点F ，CG ∥AE ，CG 交AF 于点H ，交AD 于点G . (1)求菱形ABCD 的面积； (2)求∠CHA 的度数．14题图14题答图解：(1)如图，连结AC ，∵E 为BC 的中点，AE ⊥BC ， ∴AB ＝AC .又∵菱形的边AB ＝BC ， ∴△ABC 是等边三角形，∴AE ＝32AB ＝32×4＝23，∴菱形ABCD 的面积＝BC ·AE ＝4×23＝83； (2)在等边三角形ABC 中，∵AE ⊥BC ，∴∠CAE ＝12∠BAC ＝12×60°＝30°.同理∠CAF ＝30°.∴∠EAF ＝∠CAE ＋∠CAF ＝30°＋30°＝60°. ∵AE ∥CG ，∴∠CHA ＝180°－∠EAF ＝180°－60°＝120°. C 开拓新思路 拓展创新15．如图所示，在菱形ABCD 中，∠B ＝60°，点E 在边BC 上，点F 在边CD 上． (1)如图(a)，若E 是BC 的中点，∠AEF ＝60°，求证：BE ＝DF . (2)如图(b)，若∠EAF ＝60解：(1)证明：连结AC ，∵四边形ABCD 为菱形，∠B ＝60°， ∴AB ＝BC ＝CD ，∠BCD ＝180°－∠B ＝120°， ∴△ABC 是等边三角形．∵E 是BC 的中点，∴AE ⊥BC . ∵∠AEF ＝60°，∴∠FEC ＝90°－∠AEF ＝30°，∴∠CFE ＝180°－∠FEC －∠BCD ＝180°－30°－120°＝30°， ∴∠FEC ＝∠CFE ，∴EC ＝CF ，∴BC －EC ＝DC －CF ， ∴BE ＝DF .(2)△AEF 为等边三角形．理由：连结AC ， ∵四边形ABCD 是菱形，∠B ＝60°，∴AB ＝BC ，∠D ＝∠B ＝60°，∠ACB ＝∠ACF , ∴△ABC 是等边三角形，∴AB ＝AC ，∠BAC ＝∠ACB ＝60°， ∴∠B ＝∠ACF ＝60°.∵∠BAC ＝60°＝∠BAE ＋∠EAC ，∠EAF ＝60°＝∠EAC ＋∠CAF ，∴∠BAE ＝∠CAF . 在△ABE 和△ACF 中， ∵⎩⎪⎨⎪⎧∠B ＝∠ACF ，AB ＝AC ，∠BAE ＝∠CAF ，∴△ABE ≌△ACF (ASA ), ∴AE ＝AF . 又∵∠EAF ＝60°， ∴△AEF 是等边三角形.。

∴ABD是等边三角形. AC⊥BD(菱形的对角线互相垂直)
AB=BD=6
由勾股定理,得AO= A2 B B2O 6 2 3 233
AC=2AO= 6 3
菱形面积公式的探索 菱形是特殊的平行四边形
A
那么能否利用平行四边形
菱形
面积公式计算菱形的面积吗
B
O
D
E
C
S菱形=BC. AE
为
思考:计算菱形的面积除了上式方法外,利 什
用对角线能 计算菱形的面积公式吗?
么
?
S菱形ABCD=S△ABD+S△BCD= 1 AC×BD 2
面积：S菱形=底×高=对角线乘积的一半
例：如图，菱形花坛ABCD的周长为80m， ∠ABC＝60°，沿着菱形的对角线修建了两条 小路AC和BD，求两条小路的长和花坛的面积 （ 分别精确到0.01m和0.1m 2 ）
（1）在菱形ABCD中，∠BAD=2∠B，则∠B= 60 °, △ABC是 等边 三角形，∠ABD的度数为_3_0__°____ 。
2、对于以下图形（1）矩形（2）等边三角形（3） 平行四边形（4）菱形（5）圆（6）线段， 既
是轴对称图形又是中心对称图形的有（ D）
A、1个 B、2个 C、3个 D、4个
3、已知菱形的两条对角线长分别是10和24,则
菱形的周长为__5_2__。
1.已知菱形的周长是12cm，那
么它的边长是__3_c_m__.
菱形的性质1：
菱形的四条边都相等。
B
D C
探索新知：
（1）菱形是轴对称图形吗？ 如果是，那么它有几条对称轴？ 对称轴之间有什么位置关系？
（2）如何利用折纸、剪切 的方法，既快又准确地剪出一个 菱形的纸片？

5.2.1 《菱形》教学设计教学目标：1、知识与技能：（1）理解菱形的概念；（2）掌握菱形的性质定理“菱形的四条边都相等”；（3）掌握菱形的性质定理“菱形的对角线互相垂直，并且每条对角线平分一组对角”；（4）探索并掌握菱形的对称性。

2、过程与方法目标：（1）经历菱形的概念的形成过程和性质的探究过程，培养学生的观察、推理的意识，发展学生的逻辑推理能力；（2）根据菱形的性质进行推理证明，培养学生的逻辑推理能力。

3、情感态度与价值观目标：体验数学来源于生活又服务于生活,体会菱形的对称美, 提高学生的学习兴趣。

教学重点：菱形的性质。

教学难点：本节课中的例1涉及到的知识点较多，是本节课的难点。

教学媒体：多媒体课件，几何画板。

教学过程：一、复习引入新知同学们，第四章我们已经学习了一般平行四边形的相关知识，今天就由老师带领大家一起探索特殊的平行四边形。

下面请同学们回顾我们在探索一般平行四边形时是从哪几个角度对一般平行四边形进行研究，并根据表格回顾平行四边形的性质。

当一般平行四边形有一个角是90°时，它就是我们上一节研究的矩形； 当一般平行四边形邻边相等时，它就是我们今天所要探究的特殊平行四边形─菱形。

设计意图：通过复习引入今天所要探究的特殊平行四边形─菱形，不仅复习了一般平行四边形的相关性质，而且为菱形性质的研究提供了角度。

二 、新知探究 （一）体验概念由矩形的性质可知矩形是一般平行四边形的角的特殊化，今天我们从边的特殊化来研究，请同学们仔细观察。

菱形作为一种特殊的平行四边形，你能给菱形下个定义吗？给出菱形的定义：有一组邻边相等的平行四边形是菱形。

那菱形的概念中，有哪几个关键词呢？ 从定义中可知菱形是一种特殊的平行四边形。

设计意图：使学生明确菱形也是平行四边形，借助于动画让学生发现菱形是一种邻边相等的平行四边形。

让学生根据操作体验菱形的概念，通过剖析关键词让学生认识菱形是一种特殊的平行四边形。

（二）感悟应用CAABCD在学生经历菱形的概念发现过程之后引导学生思考我们为什么学习菱形。

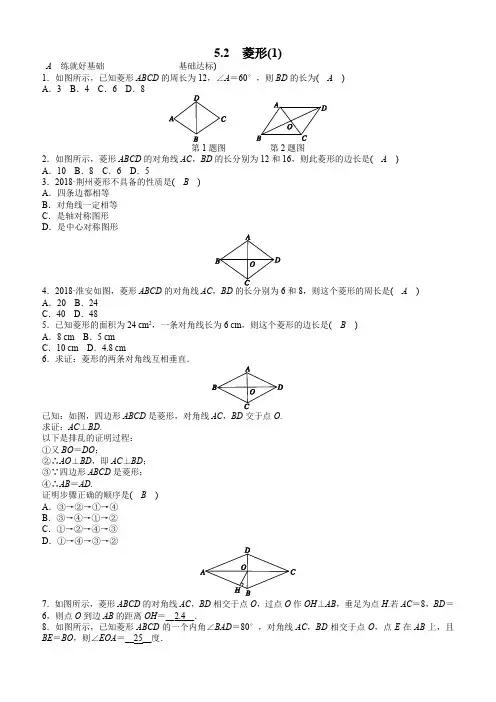
5.2菱形(1)A练就好基础基础达标)1．如图所示，已知菱形ABCD的周长为12，∠A＝60°，则BD的长为(A)A．3 B．4 C．6 D．8第1题图第2题图2．如图所示，菱形ABCD的对角线AC，BD的长分别为12和16，则此菱形的边长是(A)A．10 B．8 C．6 D．53．2018·荆州菱形不具备的性质是(B)A．四条边都相等B．对角线一定相等C．是轴对称图形D．是中心对称图形4．2018·淮安如图，菱形ABCD的对角线AC和8，则这个菱形的周长是(A)A．20 B．24C．40 D．485．已知菱形的面积为24 cm2，一条对角线长为6 cm，则这个菱形的边长是(B)A．8 cm B．5 cmC．10 cm D．4.8 cm6．求证：菱形的两条对角线互相垂直．已知：如图，四边形ABCD是菱形，对角线AC，BD交于点O.求证：AC⊥BD.以下是排乱的证明过程：①又BO＝DO；②∴AO⊥BD，即AC⊥BD；③∵四边形ABCD是菱形；④∴AB＝AD.证明步骤正确的顺序是(B)A．③→②→①→④B．③→④→①→②C．①→②→④→③D．①→④→③→②7．如图所示，菱形ABCD的对角线AC，BD相交于点O，过点O作OH⊥AB，垂足为点H.若AC＝8，BD＝6，则点O到边AB的距离OH＝__2.4__．8．如图所示，已知菱形ABCD的一个内角∠BAD＝80°，对角线AC，BD相交于点O，点E在AB上，且BE＝BO，则∠EOA＝__25__度．第9题图9．2018·广州如图，若菱形ABCD 的顶点A ，B 的坐标分别为(3，0)，(－2，0)，点D 在y 轴上，则点C 的坐标是 (－5，4) ．10. 如图所示，四边形ABCD 是菱形，DE ⊥AB 交BA 的延长线于点E ，DF ⊥BC 交BC 的延长线于点F . 求证：FC ＝AE .证明：连结BD .∵四边形ABCD 是菱形，∴BD 平分∠ABC ，AD ＝CD . 又∵DE ⊥AB ，DF ⊥BC ，∴DE ＝DF . 在Rt △ADE 和Rt △CDF 中， ∵⎩⎪⎨⎪⎧DE ＝DF ，AD ＝CD ，∴Rt △ADE ≌Rt △CDF (HL )， ∴FC ＝AE .B 更上一层楼 能力提升11．如图所示，小华剪了两条宽为1的纸条，交叉叠放在一起，且它们的交角为60°，则它们重叠部分的面积为( C ) A. 2 B ．1 C.233 D ．212．四边形BAD ＝60°，AB ＝6，对角线AC 与BD 相交于点O ，点E 在AC 上，若OE ＝3，则CE 的长为__43或23__． 【解析】∵四边形ABCD 是菱形，∴AB ＝AD ＝6，AC ⊥BD ，OB ＝OD ，OA ＝OC . ∵∠BAD ＝60°，∴△ABD 是等边三角形，∴BD ＝AB ＝6，∴OB ＝12BD ＝3，∴OC ＝OA ＝AB 2－OB 2＝33， ∵点E 在AC 上，OE ＝3，∴CE ＝OC ＋3或CE ＝OC －3， ∴CE ＝43或CE ＝2 3. 故答案为43或2 3. 13．如图所示，四边形ABCD 是菱形，对角线AC ，BD 相交于点O ，DH ⊥AB 于点H ，连结OH ，求证：∠DHO ＝∠DCO .证明：∵四边形ABCD 是菱形，∴AB ∥CD ，OD ＝OB ，∠COD ＝90°. ∵DH ⊥AB ，∴OH ＝OB . ∴∠OHB ＝∠OBH .又∵AB ∥CD ，∴∠OBH ＝∠ODC . ∴∠OHB ＝∠ODC .∵在Rt △COD 中，∠ODC ＋∠DCO ＝90°， 在Rt △DHB 中，∠DHO ＋∠OHB ＝90°， ∴∠DHO ＝∠DCO .14．如图，在菱形ABCD 中，AB ＝4，E 为BC 中点，AE ⊥BC 于点E ，AF ⊥CD 于点F ，CG ∥AE ，CG 交AF 于点H ，交AD 于点G . (1)求菱形ABCD 的面积； (2)求∠CHA 的度数．14题图14题答图解：(1)如图，连结AC ，∵E 为BC 的中点，AE ⊥BC ， ∴AB ＝AC .又∵菱形的边AB ＝BC ， ∴△ABC 是等边三角形，∴AE ＝32AB ＝32×4＝23，∴菱形ABCD 的面积＝BC ·AE ＝4×23＝83； (2)在等边三角形ABC 中，∵AE ⊥BC ，∴∠CAE ＝12∠BAC ＝12×60°＝30°.同理∠CAF ＝30°.∴∠EAF ＝∠CAE ＋∠CAF ＝30°＋30°＝60°. ∵AE ∥CG ，∴∠CHA ＝180°－∠EAF ＝180°－60°＝120°. C 开拓新思路 拓展创新15．如图所示，在菱形ABCD 中，∠B ＝60°，点E 在边BC 上，点F 在边CD 上． (1)如图(a)，若E 是BC 的中点，∠AEF ＝60°，求证：BE ＝DF . (2)如图(b)，若∠EAF ＝60解：(1)证明：连结AC ，∵四边形ABCD 为菱形，∠B ＝60°， ∴AB ＝BC ＝CD ，∠BCD ＝180°－∠B ＝120°， ∴△ABC 是等边三角形．∵E 是BC 的中点，∴AE ⊥BC . ∵∠AEF ＝60°，∴∠FEC ＝90°－∠AEF ＝30°，∴∠CFE ＝180°－∠FEC －∠BCD ＝180°－30°－120°＝30°， ∴∠FEC ＝∠CFE ，∴EC ＝CF ， ∴BC －EC ＝DC －CF ， ∴BE ＝DF .(2)△AEF 为等边三角形．理由：连结AC ， ∵四边形ABCD 是菱形，∠B ＝60°，∴AB ＝BC ，∠D ＝∠B ＝60°，∠ACB ＝∠ACF , ∴△ABC 是等边三角形，∴AB ＝AC ，∠BAC ＝∠ACB ＝60°， ∴∠B ＝∠ACF ＝60°.∵∠BAC ＝60°＝∠BAE ＋∠EAC ，∠EAF ＝60°＝∠EAC ＋∠CAF ，∴∠BAE ＝∠CAF . 在△ABE 和△ACF 中， ∵⎩⎪⎨⎪⎧∠B ＝∠ACF ，AB ＝AC ，∠BAE ＝∠CAF ，∴△ABE ≌△ACF (ASA ), ∴AE ＝AF . 又∵∠EAF ＝60°， ∴△AEF 是等边三角形.。

予以探索。
A
B
D
E
F
C M
N
布置作业
1、作业本 2、课后练习
❖1、谁要是自己还没有发展培养和教育好，他就不能发展培养和教育别人。2022年2月15日星期二2022/2/152022/2/152022/2/15 ❖2、一年之计，莫如树谷；十年之计，莫如树木；终身之计，莫如树人。2022年2月2022/2/152022/2/152022/2/152/15/2022 ❖3、提出一个问题往往比解决一个更重要。因为解决问题也许仅是一个数学上或实验上的技能而已，而提出新的问题，却需要有创造性的想像力，而且标志 着科学的真正进步。2022/2/152022/2/15February 15, 2022 ❖4、儿童是中心，教育的措施便围绕他们而组织起来。2022/2/152022/2/152022/2/152022/2/15
A
C
B
D
D
C
O
B
A
（2）已知：菱形ABCD中，对角线AC与BD相交于点O， 且 AC=12，BD=16，则菱形ABCD的面积为 40 ，边 长为 96 ，周长为 10 。
课堂检测
（3）在菱形ABCD中∠BAC=30°，BD=6㎝，则 ∠BAD= 60 ° , ∠ABD= 60 °, AB= 6㎝ .
谢谢观赏
You made my day!
我们，还在路上……
D
A
O
C
B
例1 (2)如图，菱形ABCD的边长为4cm，∠BAD ＝1200。对角线AC、BD相交于点O.
求这个菱形的对角线长和面积。
D
A
O
C
B
例1 (3)菱形ABCD的周长为16，相邻两角的度数 比为1：2． 求菱形ABCD的对角线的长；

• 14、Thank you very much for taking me with you on that splendid outing to London. It was the first time that I had seen the Tower or any of the other famous sights. If I'd gone alone, I couldn't have seen nearly as much, because I wouldn't have known my way about.
∵∠BAC=30°
线互相平分)
∴∠BAD=60° ∴ABD是等边三角形. ∴ AB=BD=6
AC⊥BD(菱形的对角线互相垂直)
由勾股定理,得AO= A2 B B2O 6 2 3 233
AC=2AO= 6 3
【菱形的面积公式】
A
菱形是特殊的平行四边形, 那么能否利用平行四边形
菱形
面积公式计算菱形的面积吗
对角线 菱形的两条对角线互相垂直AC⊥BD
平，每一条对角线平分一组对角。
想一想 矩形、菱形是不是轴对称图 形？如果是轴对称图形，对称轴各 几条
矩形是轴对称图形，对称轴有两条。 菱形是轴对称图形，对称轴有两条。
轻松小考场
面积小课堂
争分夺秒 安全出口
比一比， 哪一位同 学表现得 最出色， 得到的五 角星最多 魔力殿堂
5.2菱形（第1课时）
去参观了!
菱形具有工整,匀称,美观等许多优点, 常被人们用在图案设计上.
“法兰西巡逻兵”飞行表演队称得上是世界最著名、同时也是世界 最古老的飞行特技小组之一，他们的飞行秉承法国文化中固有的优 雅风范，编排巧妙，它的飞行表演也并不在意是否雷霆万钧气势迫

关系.
2.探索并证明菱形的性质定理： 符号语言）.
2.探索并证明菱形的性质 菱形的四条边相等．
2.学生能说出菱形的四条边相等，并
定理：菱形的四条边相等, 3.探索并证明菱形的性质定理： 给出证明.
对角线互相垂直.
对角线互相垂直，并每条对角 3. 猜想、验证、证明、归纳出菱形
3.探索菱形的轴对称性. 线平分一组对角．
对角线互相垂直，并每条对角线平分
4.探索菱形的轴对称性.
一组对角.
4.学生通过折、剪、拼明确菱形是轴
对称图形，并能说出它的对称轴.
03 教 学 问 题 诊 断 分 析
已经具备的基础
三角形的分类 和特殊三角形
的性质
平行四边形和 矩形的性质、 判定、应用
能够从边和角 考虑图形的特 殊化，知道从 边、角、对角 线和对称性研 究图形性质．
线平分一组对角．
分一组对角.
4.探索菱形的轴对称性.
菱形轴对称性难以理解
课时目标
1.理解菱形的概念， 以及菱形与平行四边 形的关系.
2.探索并证明菱形的 性质定理：菱形的四 条边相等．
3.探索并证明菱形的 性质定理：对角线互 相垂直，并且每条对 角线平分一组对角．
可能问题
教师引导
忽视菱形作为平 行四边形所具备 的一般性质.
Байду номын сангаас定性判 应 义质定 用
菱形
本节课的教学重点：探索并证明菱形的性质
02目标及目标解析
对照 课标 要求
目标确定
课标要求
课时目标
目标解析
1.理解菱形的概念，以及 1.理解菱形的概念，以及菱形 1.学生能说出菱形与平行四边形的关
菱形与平行四边形之间的 与平行四边形的关系．

5.2菱形（1）一、教学目标1、知识与技能：理解并掌握菱形的定义及性质，能够利用菱形的性质解决生活中的实际问题。

2、过程与方法：通过观察、操作和分析，得出菱形的性质，并运用菱形的性质解决相关的证明和运算。

3、情感态度与价值观：通过本课的学习，让同学们感受到生活中的菱形，其实数学和现实生活是息息相关的。

二、重点与难点1、重点：理解并掌握菱形的概念与性质。

2、难点：菱形的概念与性质在实际问题中的应用。

三、教学准备电子白板和投影仪，多媒体课件、几何模型（长方形纸片若干张），剪刀等等五、教学过程（一）复习旧知，导入新课活动1：提出问题：前面我们学习了矩形这节课，那么什么是矩形呢？学生答：矩形是有一个角是直角的平行四边形。

教师提问：既然矩形是一个特殊的平行四边形，那么我们是否还认识其它的特殊平行四边形呢？引入菱形。

活动2：让同学们自己看书，找出菱形的定义。

然后，教师讲解并总结定义。

定义：有一组邻边相等的平行四边形叫做菱形菱形的表示方法：菱形ABCD活动3：感受生活举例生活中菱形的图案，然学生自己回答，教师再展示一些图片出来，例如：（二）探究新知，加深理解活动4：折纸探究：学生在教师引导下，将一张长方形纸片连续对折两次，然后沿着右图中的虚线剪下、打开，讨论这是一个什么样的图形?引导学生操作（折叠：上下对折，左右对折），观察并思考：（1）为什么这样折叠的四边形就是菱形呢？从四条边相等出发，运用定义，说明它是一个菱形。

（2）那么它具有什么样的性质呢？（通过折纸说明）结合学生探索、讨论、交流的情况，必要时教师对知识作适当梳理，并板书菱形的性质：菱形是轴对称图形，两条对角线所在直线都是它的对称轴；菱形的四条边都相等；菱形的对角线互相垂直，并且每一条对角线平分一组对角。

（三）、例题解析：活动5：例1：如图，菱形花坛ABCD的边长为20m，∠ABC=60°，•沿着菱形的对角线修建了两条小路AC和BD，求两条小路的长和花坛的面积（分别精确到0.01m•和0.01m2）。

5.2 菱形(1)
下面图形具有工整,匀称,美观等许多 优点,常被人们用在图案设计上.
图 片 欣 赏
有一组邻边相等的平行四边形叫做菱形；
AB=BC ABCD
四边形ABCD是菱形
一、菱形的性质的研究 菱形是特殊的平行四边形， 具有平行四边形的所有性质. 由于平行四边形的对边相等，
而菱形的邻边相等，故： A
∵四边形ABCD是菱形，∴ AC⊥DB DE= A 2 A D 2 E 4 2 2 2
∵ DB=4 ∴ 0B=2
=2 3
∴ 在Rt△AOB中,由勾股定理得
∴ S菱形ABCD=4×2 3
AO= A 2 B B 2 O 4 2 2 2 2 3
=8 3
∴ AC=4 3
.
C
A
B
菱形ABCD的周长为16，相邻两角的度数比为1： 2．
⑴求菱形ABCD的对角线的长；
⑵求菱形ABCD的面积．
A
O
B
D
C
边 菱形的两组对边平行且相等 D
菱形的四条边相等
A
O
C
菱形的两组对角分别相等
B
角
菱形的邻角互补
菱形的 两条对角线互相平分
对角线 菱形的两条对角线互相垂直平分，每一 条对角线平分一组对角。
又∵ AC = AC
∴ ∠DOA=∠BOA
∴ △ADC ≌ △ABC 又∵ ∠DOA+∠BOA= 180°
∴ ∠DAC=∠BAC ∠DCA=∠BCA
∴ ∠DOA=∠BOA= 90°
已知四边形ABCD是菱形
A
D
相等的线段：AB=CD=AD=BC
12
7 8
OA=OC OB=OD

5.2菱形(1)A练就好基础基础达标)1．如图所示，已知菱形ABCD的周长为12，∠A＝60°，则BD的长为(A)A．3 B．4 C第1题图第2题图2．如图所示，菱形ABCD的对角线AC，BD的长分别为12和16，则此菱形的边长是(A)A．10 B．8 C．6 D．53．2018·荆州菱形不具备的性质是(B)A．四条边都相等B．对角线一定相等C．是轴对称图形D．是中心对称图形4．2018·淮安如图，菱形，BD的长分别为6和8，则这个菱形的周长是(A)A．20 B．24C．40 D．485．已知菱形的面积为24 cm2，一条对角线长为6 cm，则这个菱形的边长是(B)A．8 cm B．5 cmC．10 cm D．4.8 cm6．求证：菱形的两条对角线互相垂直．已知：如图，四边形ABCD是菱形，对角线AC，BD交于点O.求证：AC⊥BD.以下是排乱的证明过程：①又BO＝DO；②∴AO⊥BD，即AC⊥BD；③∵四边形ABCD是菱形；④∴AB＝AD.证明步骤正确的顺序是(B)A．③→②→①→④B．③→④→①→②C．①→②→④→③D．①→④→③→②7．如图所示，菱形ABCD的对角线AC，BD相交于点O，过点O作OH⊥AB，垂足为点H.若AC＝8，BD＝6，则点O到边AB的距离OH＝__2.4__．8．如图所示，已知菱形ABCD的一个内角∠BAD＝80°，对角线AC，BD相交于点O，点E在AB上，且BE＝BO，则∠EOA＝__25__度．8题图第9题图9．2018·广州如图，若菱形ABCD的顶点A，B的坐标分别为(3，0)，(－2，0)，点D在y轴上，则点C的坐标是(－5，4)．10. 如图所示，四边形ABCD是菱形，DE⊥AB交BA的延长线于点E，DF⊥BC交BC的延长线于点F.求证：FC＝AE.证明：连结BD.∵四边形ABCD是菱形，∴BD平分∠ABC，AD＝CD.又∵DE⊥AB，DF⊥BC，∴DE＝DF.在Rt△ADE和Rt△CDF中，∵⎩⎪⎨⎪⎧DE ＝DF ，AD ＝CD ，∴Rt △ADE ≌Rt △CDF (HL )， ∴FC ＝AE .B 更上一层楼 能力提升11．如图所示，小华剪了两条宽为1的纸条，交叉叠放在一起，且它们的交角为60°，则它们重叠部分的面积为( C )A. 2 B ．1C.233 D ．212．四边形ABCD 是菱形，∠BAD ＝60°，AB ＝6，对角线AC 与BD相交于点O ，点E 在AC 上，若OE ＝3，则CE 的长为__．【解析】∵四边形ABCD 是菱形，∴AB ＝AD ＝6，AC ⊥BD ，OB ＝OD ，OA ＝OC .∵∠BAD ＝60°，∴△ABD 是等边三角形，∴BD ＝AB ＝6，∴OB ＝12BD ＝3，∴OC ＝OA ＝AB 2－OB 2＝33，∵点E 在AC 上，OE ＝3，∴CE ＝OC ＋3或CE ＝OC －3，∴CE ＝43或CE ＝2 3.故答案为43或2 3.13．如图所示，四边形ABCD 是菱形，对角线AC ，BD 相交于点O ，DH ⊥AB 于点H ，连结OH ，求证：∠DHO ＝∠DCO .证明：∵四边形ABCD 是菱形，∴AB ∥CD ，OD ＝OB ，∠COD ＝90°.∵DH ⊥AB ，∴OH ＝OB .∴∠OHB ＝∠OBH .又∵AB ∥CD ，∴∠OBH ＝∠ODC .∴∠OHB ＝∠ODC .∵在Rt △COD 中，∠ODC ＋∠DCO ＝90°，在Rt △DHB 中，∠DHO ＋∠OHB ＝90°，∴∠DHO ＝∠DCO .14．如图，在菱形ABCD 中，AB ＝4，E 为BC 中点，AE ⊥BC 于点E ，AF ⊥CD 于点F ，CG ∥AE ，CG 交AF 于点H ，交AD 于点G .(1)求菱形ABCD 的面积；(2)求∠CHA14题图14题答图解：(1)如图，连结AC ，∵E 为BC 的中点，AE ⊥BC ，∴AB ＝AC .又∵菱形的边AB ＝BC ，∴△ABC 是等边三角形，∴AE ＝32AB ＝32×4＝23，∴菱形ABCD 的面积＝BC ·AE ＝4×23＝83；(2)在等边三角形ABC 中，∵AE ⊥BC ，∴∠CAE ＝12∠BAC ＝12×60°＝30°.同理∠CAF ＝30°.∴∠EAF ＝∠CAE ＋∠CAF ＝30°＋30°＝60°.∵AE ∥CG ，∴∠CHA ＝180°－∠EAF ＝180°－60°＝120°.C 开拓新思路 拓展创新15．如图所示，在菱形ABCD 中，∠B ＝60°，点E 在边BC 上，点F 在边CD 上．(1)如图(a)，若E 是BC 的中点，∠AEF ＝60°，求证：BE ＝DF .(2)如图(b)，若∠EAF ＝60°，试判定△AEF 的形状并说明理由．解：(1)证明：连结AC ，∵四边形ABCD 为菱形，∠B ＝60°，∴AB ＝BC ＝CD ，∠BCD ＝180°－∠B ＝120°，∴△ABC 是等边三角形．∵E 是BC 的中点，∴AE ⊥BC .∵∠AEF ＝60°，∴∠FEC ＝90°－∠AEF ＝30°，∴∠CFE ＝180°－∠FEC －∠BCD ＝180°－30°－120°＝30°， ∴∠FEC ＝∠CFE ，∴EC ＝CF ，∴BC －EC ＝DC －CF ，∴BE ＝DF .(2)△AEF 为等边三角形．理由：连结AC ，∵四边形ABCD 是菱形，∠B ＝60°，∴AB ＝BC ，∠D ＝∠B ＝60°，∠ACB ＝∠ACF ,∴△ABC 是等边三角形，∴AB ＝AC ，∠BAC ＝∠ACB ＝60°，∴∠B ＝∠ACF ＝60°.∵∠BAC ＝60°＝∠BAE ＋∠EAC ，∠EAF ＝60°＝∠EAC ＋∠CAF ，∴∠BAE ＝∠CAF .在△ABE 和△ACF 中，∵⎩⎪⎨⎪⎧∠B ＝∠ACF ，AB ＝AC ，∠BAE ＝∠CAF ，∴△ABE ≌△ACF (ASA ), ∴AE ＝AF .又∵∠EAF ＝60°，∴△AEF 是等边三角形.。

6.2 菱形(2)【教学目标】1．经历菱形的判定定理的发现过程。

2．掌握菱形的判定定理“四条边相等的四边形是菱形”。

3．掌握菱形的判定定理“对角线互相垂直的平行四边形是菱形”。

4．通过运用菱形知识解决具体问题，提高分析能力和观察能力．并根据平行四边形、矩形、菱形的从属关系，向学生渗透集合思想．【教学重点、难点】重点：菱形的判定定理．难点：菱形判定方法的综合应用．课本“合作学习”既需要一定的空间想象力，又要有较强的逻辑思维能力．【教学方法】启发诱导、讨论、讲授相结合【教学过程】(一)、复习引入1、提问菱形的定义和性质。

定义：一组邻边对应相等的平行四边形叫做菱形。

性质：除具备一般平行四边形的性质外，还具备四条边相等，对角线互相垂直，并且每条对角线平分一组对角判定一个四边形是不是菱形可根据什么来判定？定义，此外还有两种判定方法，今天我们就要学习菱形的判定。

（板书课题）(二)、创设情境，引入新课1、合作学习：学生拿出准备好的长方形纸片，按图6-15（P142）的方法对折两次，并沿（3）中的斜线剪开，展开剪下的部分，猜想这个图形是哪一种四边形？一定是菱形吗？为什么？剪出的图形四条边都相等，根据这个条件首先证它是平行四边形，再证一组邻边相等，依定义即知为菱形．结论：菱形判定定理1：四边都相等的四边形是菱形（板书）(三)、交流互动，探求新知1、已知：如图，在ABCD中，BD⊥AC，O为垂足。

求证：ABCD是菱形启发：在已知是平行四边形的情况下，要证明是菱形，只要证明一组邻边相等。

证明：∵四边形ABCD是平行四边形，∴AO＝CO（平行四边形的对角线互相平分）。

∵BD⊥AC，∴AD＝CD∴A BCD是菱形（菱形的定义）。

结论：菱形判定定理2：对角线互相垂直的平行四边形是菱形。

2、猜想：对角线互相垂直平分的四边形是不是菱形？启发：通过四个直角三角形的全等得到四条边相等。

结论：对角线互相垂直平分的四边形是菱形。

3、例2：如图，在矩形ABCD中，对角线AC的垂直平分线与AD，BC分别交于点E，F ，求证：四边形AFCE是菱形。

• 2、能够运用菱形性质(xìngzhì)解决具 体问题。
第三页，共16页。
B
C
A
D
一组邻边相等的平行 四边形叫做(jiàozuò)
第四页，共16页。
第五页，共16页。
第六页，共16页。
“法兰西巡逻兵”飞行表演队称得上是世界最著名、同时也是世界最 古老的飞行特技小组之一，他们的飞行秉承法国文化中固有的优雅风 范，编排巧妙，它的飞行表演也并不在意是否雷霆万钧气势迫人，而
5.2 菱形(línɡ xínɡ)
(第一课时)
第一页，共16页。
矩形(jǔxíng)
有一个角是直角(zhíjiǎo)的平行四边形叫 做矩形。
矩形是一个(yī ɡè)特殊的平行四边形， 那么
还有其它的特殊的平行四边形吗？
第二页，共16页。
学习(xuéxí)目标
• 1、理解并掌握菱形的定义及性质 (xìngzhì)；
A D
2.菱形(línɡ xínɡ)ABCD中∠ABC＝
60度，则∠BA6C0＝度_______.
O
C B
3.菱形的两条对角线的长分别为6cm和 想一想 8cm，那么菱形的面积是_____2.4cm2
有关(yǒuguān)菱形问题可转化为直角 三角形或等腰三角形的问题来解决
第十五页，共16页。
谢谢(xiè ie)!
1、有一组邻边相等的四边形是菱形。( ×) 2、菱形是平行四边形。( √)
二. 菱形(línɡ xínɡ)ABCD中,O是两
条对角线的交点，已知AB＝
5_c_m_,_8B,OBc=Dm的4c长m，为则__对__角_线。6AcmC的长为
第十三页，共16页。
第十四页，共16页。
作业

证明： ∵四边形ABCD是菱形
倍 速 课 时 学 练
∴AB=AD,OD=OB
又∵ AO = AO ∴AB=BC=CD=DA ∴ △AOD ≌ △AOB 又∵ AC = AC ∴ ∠DOA=∠BOA ∴ △ADC ≌ △ABC 又∵ ∠DOA+∠BOA= 18 ∴ ∠DOA=∠BOA= 90 ∴ ∠DAC=∠BAC ∠DCA=∠BCA
解:∵四边形ABCD是菱形, ∴AB=CD(菱形的定义) AC平分∠BAD(菱形的每条对角线平分一组对角) ∵∠BAC=30° 又∵OB=OD=3(平行四边形的对角 线互相平分)
∠BAD=60°
∴ABD是等边三角形. AC⊥BD(菱形的对角线互相垂直) 由勾股定理,得AO= AB2 BO2 62 32 3 3 AB=BD=6 AC=2AO= 6 3
相等的线段：
已知四边形ABCD是菱形 AB=CD=AD=BC OA=OC OB=OD
B
5 6
A
1 2
7
8
O
3 4
∠DAB=∠BCD ∠ABC =∠CDA 相等的角：
C
∠AOB=∠DOC=∠AOD=∠BOC =90° ∠1=∠2=∠3=∠4
倍 速 课 时 学 练
∠5=∠6=∠7=∠8
等腰三角形有： △ABC △ DBC △ACD △ABD Rt△AOB Rt△BOC Rt△COD 直角三角形有： Rt△DOA
倍 速 课 时 学 练
B E C M F
D
N
2.菱形ABCD中 ∠ABC=60°,AB=4cm,P为BD上任意 一点,E为BC中点,求PE+PC的最小值.
A B E C P D
倍 速 课 时 学 练
他是这样做的：将一张长方形的纸 对折、再对折，然后沿图中的虚线剪下， 打开即可.你知道其中的道理吗？