色度图
- 格式:doc
- 大小:475.00 KB
- 文档页数:16

颜⾊基础知识——CIE1931⾊度坐标图CIE 1931⾊度坐标介绍1. 意义图中的颜⾊,包括了⾃然所能得到的颜⾊。
这是个⼆维平⾯空间图,由x-y直⾓标系统构成的平⾯。
为了适应⼈们习惯于在平⾯坐标系中讨论变量关系,⽽设计出来的。
在设计出该图的过程中,经过许多数学上的变换和演算。
此图的意义和作⽤,可以总结成两句话:(1)表⽰颜⾊视觉的基本规律。
(2)表⽰颜⾊混合与分解的⼀般规律。
2. 坐标系——x ,y直⾓坐标系。
x——表⽰与红⾊有关的相对量值。
y——表⽰与绿⾊有关的相对量值。
z——表⽰与蓝⾊有关的相对量值。
并且z=1-(x+y)3. 形状与外形轮廓线形状——⾆形,有时候也称“⾆形曲线”图。
由⾆形外围曲线和底部直线包围起来的闭合区域。
⾆形外围曲线——是全部可见光单⾊光颜⾊轨迹线,每⼀点代表某个波长单⾊光的颜⾊,波长从390nm到760nm。
在曲线的旁边。
标注了⼀些特征颜⾊点的对应波长。
例如图中510nm——520nm——530nm等。
底部直线——连接390nm点到760nm点构成的直线,此线称为紫红线。
4. ⾊彩这是⼀个彩⾊图,区域内的⾊彩,包括了⼀切物理上能实现的颜⾊。
很遗憾的是,很难得真正标准的这种资料,经常由于转印⽽失真。
5. 应⽤价值——颜⾊的定量表⽰。
⽤(x,y)的坐标值来表⽰颜⾊。
⽩⾊应该包含在“颜⾊”这个概念范围内。
6. 若⼲个特征点的意义(1)E点—等能⽩光点的坐标点E点是以三种基⾊光,以相同的刺激光能量混合⽽成的。
但三者的光通量并不相等。
E点的CCT=5400K。
(2)A点—CIE规定⼀种标准⽩光光源的⾊度坐标点这是⼀种纯钨丝灯,⾊温值CCT=2856。
(3)B点—CIE规定的⼀种标准光源坐标点B点的CCT=4874K,代表直射⽇光。
(4)C点—CIE确认的⼀种标准⽇光光源坐标点(昼光)C点的CCT=6774K。
(5)D点—有时候也标为D光源称为典型⽇光,或重组⽇光;CCT=6500K。
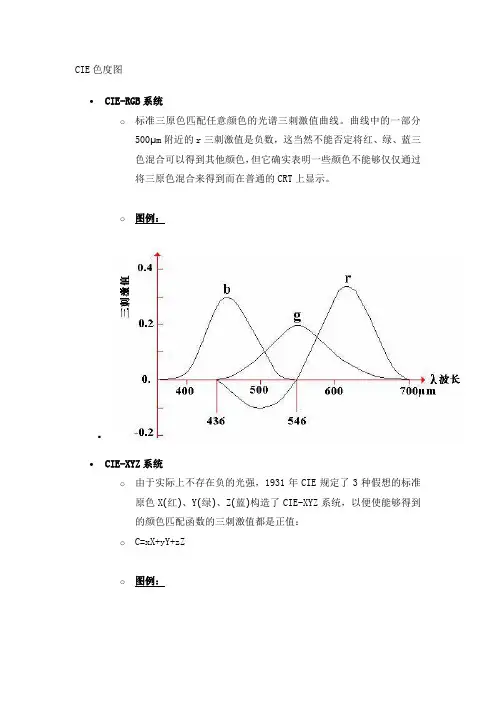
CIE色度图∙CIE-RGB系统o标准三原色匹配任意颜色的光谱三刺激值曲线。
曲线中的一部分500μm附近的r三刺激值是负数,这当然不能否定将红、绿、蓝三色混合可以得到其他颜色,但它确实表明一些颜色不能够仅仅通过将三原色混合来得到而在普通的CRT上显示。
o图例:∙CIE-XYZ系统o由于实际上不存在负的光强,1931年CIE规定了3种假想的标准原色X(红)、Y(绿)、Z(蓝)构造了CIE-XYZ系统,以便使能够得到的颜色匹配函数的三刺激值都是正值:o C=xX+yY+zZo图例:▪三刺激空间和色度图o所有颜色向量组成了x>0、y>0和z>0的三维空间第一象限锥体o取一个截面 x+y+z=1o该截面与三个坐标平面的交线构成一个等边三角形,每一个颜色向量与该平面都有一个交点,每一个点代表一个颜色,它的空间坐标(x,y,z)表示为该颜色在标准原色下的三刺激值,称为色度值o图例:▪▪∙CIE色度图o CIE色度图的翼形轮廓线代表所有可见光波长的轨迹,即可见光谱曲线。
o沿线的数字表示该位置的可见光的主波长。
o中央的C对应于近似太阳光的标准白光,C点接近于但不等于x=y=z=1/3的点。
o红色区域位于图的右下角,绿色区域在图的顶端,蓝色区域在图的左下角,连接光谱轨迹两端点的直线称为紫色线。
∙用途o得到光谱色的互补色,只要从该颜色点过C点作一条直线,求其与对侧光谱曲线的交点,即可得到补色的波长。
D的补色为E。
o确定所选颜色的主波长和纯度。
颜色A的主波长,从标准白光点C 过A作直线与光谱曲线相交于B(A与B在C的同侧),这样颜色A可以表示为纯色光B和白光C的混合,B就定义了颜色A的主波长。
oo定义一个颜色域。
通过调整混合比例,任意两种颜色:o I和J加在一起能够产生它们连线上的颜色o再加入第三种颜色K,就产生三者(I、J和K)构成的三角形区域的颜色。
应用限制o色度图的形状表明,没有一个3个顶点均在可见光翼形区的三角形可以完全覆盖该区域。

CIE开放分类:颜色、国际组织CIE(国际发光照明委员会):原文为Commission Internationale deL'Eclairage(法)或International Commission on Illumination(英)。
这个委员会创建的目的是要建立一套界定和测量色彩的技术标准。
可回溯到1930年,CIE标准一直沿用到数字视频时代,其中包括白光标准(D65)和阴极射线管(CRT)内表面红、绿、蓝三种磷光理论上的理想颜色。
CIE的总部位于奥地利维也纳。
CIE颜色系统颜色是一门很复杂的学科,它涉及到物理学、生物学、心理学和材料学等多种学科。
颜色是人的大脑对物体的一种主观感觉,用数学方法来描述这种感觉是一件很困难的事。
现在已经有很多有关颜色的理论、测量技术和颜色标准,但是到目前为止,似乎还没有一种人类感知颜色的理论被普遍接受。
RGB模型采用物理三基色,其物理意义很清楚,但它是一种与设备相关的颜色模型。
每一种设备(包括人眼和现在使用的扫描仪、监视器和打印机等)使用RGB模型时都有不太相同的定义,尽管各自都工作很圆满,而且很直观,但不能相互通用。
1)简介为了从基色出发定义一种与设备无关的颜色模型,1931年9月国际照明委员会在英国的剑桥市召开了具有历史意义的大会。
CIE的颜色科学家们企图在RGB模型基础上,用数学的方法从真实的基色推导出理论的三基色,创建一个新的颜色系统,使颜料、染料和印刷等工业能够明确指定产品的颜色。
会议所取得的主要成果包含:定义了标准观察者(Standard Observer)标准:普通人眼对颜色的响应。
该标准采用想象的X,λ Y和Z三种基色,用颜色匹配函数(color-matching function)表示。
颜色匹配实验使用2°的视野(field of view);定义了标准光源(Standard Illuminants):用于比较颜色的光源规范;λ定义了CIE XYZ基色系统:与RGB相关的想象的基色系统,但更适用于颜色的计算;λ定义了CIE xyY颜色空间:一个由XYZ导出的颜色空间,它把与颜色属性相关的x和y从与λ明度属性相关的亮度Y中分离开;定义了CIE色度图(CIE chromaticity diagram):容易看到颜色之间关系的一种图。

色度图波长对应坐标值部门: xxx时间: xxx整理范文,仅供参考,可下载自行编辑二、 1931CIE-XYZ标准色度系统所谓1931CIE-XYZ系统,就是在RGB系统的基础上,用数学方法,选用三个理想的原色来代替实际的三原色,从而将CIE-RGB系统中的光谱三刺激值和色度坐标r、g、b均变为正值。
<一)、CIE-RGB系统与CIE-XYZ系统的转换关系选择三个理想的原色<三刺激值)X、Y、Z,X代表红原色,Y代表绿原色,Z代表蓝原色,这三个原色不是物理上的真实色,而是虚构的假想色。
它们在图5-27中的色度坐标分别为:从图5-27中可以看到由XYZ形成的虚线三角形将整个光谱轨迹包含在内。
因此整个光谱色变成了以XYZ三角形作为色域的域内色。
在XYZ系统中所得到的光谱三刺激值、、、和色度坐标x、y、z将完全变成正值。
经数学变换,两组颜色空间的三刺激值有以下关系:X=0.490R+0.310G+0.200BY=0.177R+0.812G+0.011B …………………………<5-8)Z= 0.010G+0.990B两组颜色空间色度坐标的相互转换关系为:x=<0.490r+0.310g+0.200b)/<0.667r+1.132g+1.200b)y=<0.117r+0.812g+0.010b)/<0.667r+1.132g+1.200b)………………(5-9>z=<0.000r+0.010g+0.990b)/<0.667r+1.132g+1.200b)这就是我们通常用来进行变换的关系式,所以,只要知道某一颜色的色度坐标r、g、b,即可以求出它们在新设想的三原色XYZ颜色空间的的色度坐标x、y、z。
通过式<5-9)的变换,对光谱色或一切自然界的色彩而言,变换后的色度坐标均为正值,而且等能白光的色度坐标仍然是<0.33,0.33),没有改变。
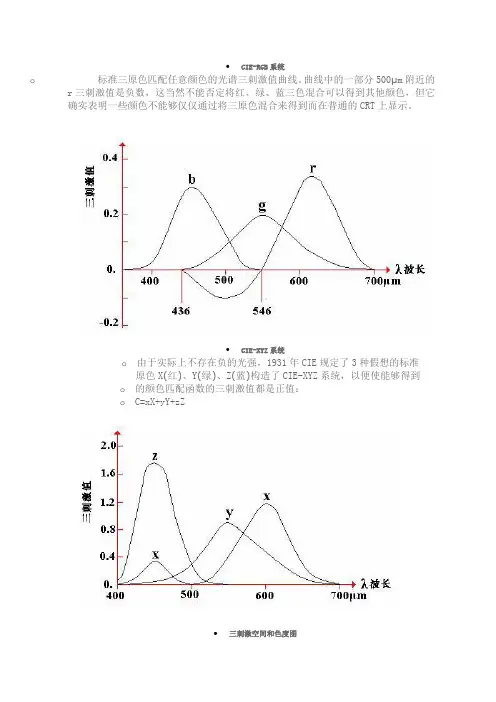
∙CIE-RGB系统o标准三原色匹配任意颜色的光谱三刺激值曲线。
曲线中的一部分500μm附近的r三刺激值是负数,这当然不能否定将红、绿、蓝三色混合可以得到其他颜色,但它确实表明一些颜色不能够仅仅通过将三原色混合来得到而在普通的CRT上显示。
∙CIE-XYZ系统o由于实际上不存在负的光强,1931年CIE规定了3种假想的标准原色X(红)、Y(绿)、Z(蓝)构造了CIE-XYZ系统,以便使能够得到o的颜色匹配函数的三刺激值都是正值:o C=xX+yY+zZ∙三刺激空间和色度图o所有颜色向量组成了x>0、y>0和z>0的三维空间第一象限锥体取一个截面 x+y+z=1该截面与三个坐标平面的交线构成一个等边三角形,每一个颜色向量与该平面都有一个交点,每一个点代表一个颜色,它的空间坐标(x,y,z)表示为该颜色在标准原色下的三刺激值,称为色度值▪▪∙CIE色度图∙CIE色度图的翼形轮廓线代表所有可见光波长的轨迹,即可见光谱曲线沿∙线的数字表示该位置的可见光的主波长。
∙中央的C对应于近似太阳光的标准白光,C点接近于但不等于x=y=z=1/3的点。
红色区域位于图的右下角,绿色区域在图的顶端,蓝色区域在图的左下角,连接光谱轨迹两端点的直线称为紫色线。
∙用途∙得到光谱色的互补色,只要从该颜色点过C点作一条直线,求其与对侧谱∙曲线的交点,即可得到补色的波长。
D的补色为E。
确定所选颜色的主波长和纯度。
颜色A的主波长,从标准白光点C过A作直线与光谱曲线相交于B(A与B在C的同侧),这样颜色A可以表示为纯色光B和白光C的混合,B就定义了颜色A的主波长。
∙定义一个颜色域。
通过调整混合比例,任意两种颜色:I和J加在一起能够产生它们连线上的颜色再加入第三种颜色K,就产生三者(I、J和K)构成的三角形区域的颜色。
应用限制色度图的形状表明,没有一个3个顶点均在可见光翼形区的三角形可以完全覆盖该区域。
因此,可见的红、绿、蓝三种颜色不能通过加法混合来匹配所有的颜色。

色度图波长对应坐标值部门: xxx时间: xxx整理范文,仅供参考,可下载自行编辑二、 1931CIE-XYZ标准色度系统所谓1931CIE-XYZ系统,就是在RGB系统的基础上,用数学方法,选用三个理想的原色来代替实际的三原色,从而将CIE-RGB系统中的光谱三刺激值和色度坐标r、g、b均变为正值。
<一)、CIE-RGB系统与CIE-XYZ系统的转换关系选择三个理想的原色<三刺激值)X、Y、Z,X代表红原色,Y代表绿原色,Z代表蓝原色,这三个原色不是物理上的真实色,而是虚构的假想色。
它们在图5-27中的色度坐标分别为:从图5-27中可以看到由XYZ形成的虚线三角形将整个光谱轨迹包含在内。
因此整个光谱色变成了以XYZ三角形作为色域的域内色。
在XYZ系统中所得到的光谱三刺激值、、、和色度坐标x、y、z将完全变成正值。
经数学变换,两组颜色空间的三刺激值有以下关系:X=0.490R+0.310G+0.200BY=0.177R+0.812G+0.011B …………………………<5-8)Z= 0.010G+0.990B两组颜色空间色度坐标的相互转换关系为:x=<0.490r+0.310g+0.200b)/<0.667r+1.132g+1.200b)y=<0.117r+0.812g+0.010b)/<0.667r+1.132g+1.200b)………………(5-9>z=<0.000r+0.010g+0.990b)/<0.667r+1.132g+1.200b)这就是我们通常用来进行变换的关系式,所以,只要知道某一颜色的色度坐标r、g、b,即可以求出它们在新设想的三原色XYZ颜色空间的的色度坐标x、y、z。
通过式<5-9)的变换,对光谱色或一切自然界的色彩而言,变换后的色度坐标均为正值,而且等能白光的色度坐标仍然是<0.33,0.33),没有改变。
几种典型的颜色空间(一)CIE色度模型国际照明委员会(CIE,Commission Internationale de L'Eclairage / International Commission on Illumination)的色度模型是最早使用的模型之一。
它是三维模型,其中,x和y两维定义颜色,第3维定义亮度。
CIE 在1976 年规定了两种颜色空间。
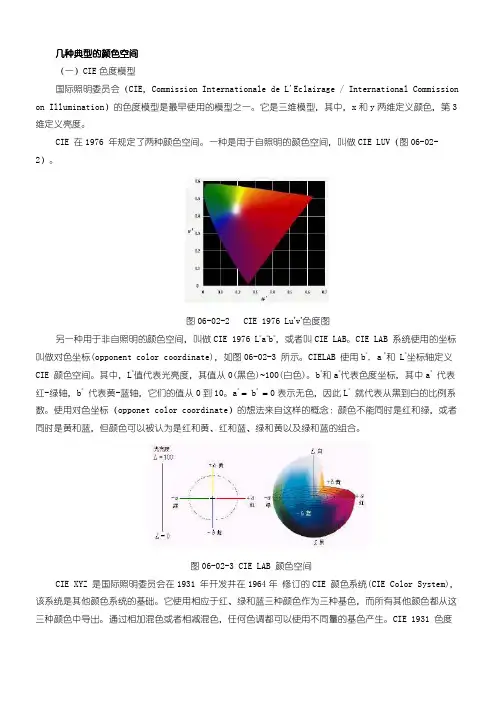
一种是用于自照明的颜色空间,叫做CIE LUV(图06-02-2)。
图06-02-2 CIE 1976 Lu’v’色度图另一种用于非自照明的颜色空间,叫做CIE 1976 L*a*b*,或者叫CIE LAB。
CIE LAB 系统使用的坐标叫做对色坐标(opponent color coordinate),如图06-02-3 所示。
CIELAB 使用b*, a *和 L*坐标轴定义CIE 颜色空间。
其中,L*值代表光亮度,其值从0(黑色)~100(白色)。
b*和a*代表色度坐标,其中a*代表红-绿轴,b*代表黄-蓝轴,它们的值从0到10。
a* = b*= 0表示无色,因此L*就代表从黑到白的比例系数。
使用对色坐标(opponet color coordinate)的想法来自这样的概念:颜色不能同时是红和绿,或者同时是黄和蓝,但颜色可以被认为是红和黄、红和蓝、绿和黄以及绿和蓝的组合。
图06-02-3 CIE LAB 颜色空间CIE XYZ 是国际照明委员会在1931 年开发并在1964年修订的CIE 颜色系统(CIE Color System),该系统是其他颜色系统的基础。
它使用相应于红、绿和蓝三种颜色作为三种基色,而所有其他颜色都从这三种颜色中导出。
通过相加混色或者相减混色,任何色调都可以使用不同量的基色产生。
CIE 1931 色度图(CIE 1931 Chromaticity Diagram),如图06-02-4(a)所示,图(b)是它的轮廓图。

cie1931标准色度观察者曲线
CIE1931标准色度观察者曲线是指在CIE1931 RGB色度图上,380nm 至780nm的光谱色所形成的轨迹曲线。
该曲线上的任意两点之间所连成的线段,覆盖的范围就是人眼能看见的所有颜色的区域大小,代表了人眼分辨颜色的极限。
在这条曲线中,380nm和780nm之间的连线构成了色域的另一个边界。
不过,上面边界的曲线是和单色光一一对应的,而下面边界的这条直线却没有单色光对应,而是两个光谱色的混合色轨迹,主要呈现紫色。
这意味着,没有单色光形成的紫色,所有带紫的颜色,如紫红色、品红色等,都属于谱外色。
CIE1931标准色度观察者曲线是一种重要的颜色表示方式,广泛应用于颜色科学和视觉感知领域。



色度图波长对应坐标值部门: xxx时间: xxx整理范文,仅供参考,可下载自行编辑二、 1931CIE-XYZ标准色度系统所谓1931CIE-XYZ系统,就是在RGB系统的基础上,用数学方法,选用三个理想的原色来代替实际的三原色,从而将CIE-RGB系统中的光谱三刺激值和色度坐标r、g、b均变为正值。
<一)、CIE-RGB系统与CIE-XYZ系统的转换关系选择三个理想的原色<三刺激值)X、Y、Z,X代表红原色,Y代表绿原色,Z代表蓝原色,这三个原色不是物理上的真实色,而是虚构的假想色。
它们在图5-27中的色度坐标分别为:从图5-27中可以看到由XYZ形成的虚线三角形将整个光谱轨迹包含在内。
因此整个光谱色变成了以XYZ三角形作为色域的域内色。
在XYZ系统中所得到的光谱三刺激值、、、和色度坐标x、y、z将完全变成正值。
经数学变换,两组颜色空间的三刺激值有以下关系:X=0.490R+0.310G+0.200BY=0.177R+0.812G+0.011B …………………………<5-8)Z= 0.010G+0.990B两组颜色空间色度坐标的相互转换关系为:x=<0.490r+0.310g+0.200b)/<0.667r+1.132g+1.200b)y=<0.117r+0.812g+0.010b)/<0.667r+1.132g+1.200b)………………(5-9>z=<0.000r+0.010g+0.990b)/<0.667r+1.132g+1.200b)这就是我们通常用来进行变换的关系式,所以,只要知道某一颜色的色度坐标r、g、b,即可以求出它们在新设想的三原色XYZ颜色空间的的色度坐标x、y、z。
通过式<5-9)的变换,对光谱色或一切自然界的色彩而言,变换后的色度坐标均为正值,而且等能白光的色度坐标仍然是<0.33,0.33),没有改变。
一、顏色之表示-色度圖(Chromaticity Diagram)在日常生活中我們會說幫我買「紅」色衣服,以工程背景的人會疑惑的反問是哪種「紅」?聖誕紅?粉紅?桃紅?朱紅?淡紅?深紅?所以人們用孟塞爾的色度圖,利用三度空間(圓柱座標)(見圖1)以角度( )方向代表紅、橙、黃、綠…等不同顏色色調(Hue),而以距離(r)表示彩度或純度(以C表示),高度代表明亮度(用V表示),H V/C表示一個顏色。
例如作為計算演色係數之色票5Y 6/4即色調H為5Y(即介於黃色10Y與紅黃色10YR之中間色)、亮度為6、飽和度為4之一個顏色。
這個用於印刷染料界很廣,但對於學工程最普遍的說法是,以一個顏色系統當作座標,你告訴我一個之色座標,則每一個人均可精確的理解你要的是什麼顏色。
顏色係人眼睛內之L,M,S錐狀體作用而形成,故人眼對顏色反應(類似於系統之脈衝響應),必須先探討,就像一個二極體對電壓、電流之特性參數,為了要取得這些參數必須做一連串之實驗以獲得相關之參數。
同樣地,人眼對R、G、B色之反應如何,也必須做一連串之配色實驗(color matching experiment),透過這些實驗來得到人眼對不同波長之反應參數,利用人眼對不同顏色之波長的反應,可將一個顏色對應到一個座標,而用座標表示顏色。
【圖1】Munsell色度圖二、加法混光配色實驗人眼在中心窩︒2內光的加法(含亮度)成立,而加法混光意味著加法必須成立,也就是格拉斯曼定理(Grassman’s law)要成立即:-對稱性: U=V ó V=U -遞移性: U=V 和 V=W => U=W -比例性: U=V ó tU=tV-疊加性: 若以下敘述中的任意兩個成立:U=V, W=X (U+W)=(V+X) 則第三個敘述必成立。
這些論述的真實性與任何生物學上定律的真實性是一樣的,說明了色彩疊加時是以線性的方式相加,這限制在視場︒2內。
⾊度图绘制close all; clear all; clccleardata=[380 0.1741 0.0050; %波长380nm~780nm x,y data385 0.1740 0.0050;390 0.1738 0.0049;395 0.1736 0.0049;400 0.1733 0.0048;405 0.1730 0.0048;410 0.1726 0.0048;415 0.1721 0.0048;420 0.1714 0.0051;425 0.1703 0.0058;430 0.1689 0.0069;435 0.1669 0.0086;440 0.1644 0.0109;445 0.1611 0.0138;450 0.1566 0.0177;455 0.1510 0.0227;460 0.1440 0.0297;465 0.1355 0.0399;470 0.1241 0.0578;475 0.1096 0.0868;480 0.0913 0.1327;485 0.0687 0.2007;490 0.0454 0.2950;495 0.0235 0.4127;500 0.0082 0.5384;505 0.0039 0.6548;510 0.0139 0.7502;515 0.0389 0.8120;520 0.0743 0.8338;525 0.1142 0.8262;530 0.1547 0.8059;535 0.1929 0.7816;540 0.2296 0.7543;545 0.2658 0.7243;550 0.3016 0.6923;555 0.3373 0.6589;560 0.3731 0.6245;565 0.4087 0.5896;570 0.4441 0.5547;575 0.4788 0.5202;580 0.5125 0.4866;585 0.5448 0.4544;590 0.5752 0.4242;595 0.6029 0.3965;600 0.6270 0.3725;605 0.6482 0.3514;610 0.6658 0.3340;615 0.6801 0.3197;620 0.6915 0.3083;625 0.7006 0.2993;630 0.7079 0.2920;635 0.7140 0.2859;640 0.7190 0.2809;645 0.7230 0.2770;650 0.7260 0.2740;655 0.7283 0.2717;660 0.7300 0.2700;665 0.7311 0.2689;670 0.7320 0.2680;675 0.7327 0.2673;680 0.7334 0.2666;685 0.7340 0.2660;690 0.7344 0.2656;695 0.7346 0.2654;700 0.7347 0.2653;705 0.7347 0.2653;710 0.7347 0.2653;715 0.7347 0.2653;720 0.7347 0.2653;725 0.7347 0.2653;730 0.7347 0.2653;735 0.7347 0.2653;740 0.7347 0.2653;745 0.7347 0.2653;750 0.7347 0.2653;755 0.7347 0.2653;760 0.7347 0.2653;765 0.7347 0.2653;770 0.7347 0.2653;775 0.7347 0.2653;780 0.7347 0.2653];l=data(:,1);x=data(:,2);y=data(:,3); %插值加密⾊度图边缘li=min(l):0.2:max(l);ll=ceil(length(li)/3);xi=interp1(l,x,li,'pchip');yi=interp1(l,y,li,'pchip');xii=linspace(x(end),x(1),ll);yii=linspace(y(end),y(1),ll);li=[li, max(li)+(1:ll-2)];xi=[xi,xii(2:end-1)];yi=[yi,yii(2:end-1)];R=700;G=546;B=436; %三基⾊颜⾊的波长RG=fliplr(find(li>G&li<=R));GB=fliplr(find(li>B&li<=G));BR=fliplr([find(li>=R),find(li<=B)]);li=li([RG GB BR]);xi=xi([RG GB BR]);yi=yi([RG GB BR]);%将边缘顺序调整为R-G-B-R⼀圈RG=1:(length(RG)+1);GB=length(RG)+(1:length(GB)+1);BR=length(RG)+length(GB)-2+(1:length(BR));ti=unwrap(atan2(yi-1/3,xi-1/3));%计算边缘以(1/3,1/3)为中⼼的⾓度ti=ti-ti(1);tt=ti(1:end-1)+diff(ti)/2;H=interp1([ti(RG(1)),ti(RG(end))],[0,1/3],tt(RG(1:end-1)));%插值计算各个⽅向的颜⾊H=[H, interp1([ti(GB(1)),ti(GB(end))],[1/3,2/3],tt(GB(1:end-1)))];H=[H, interp1([ti(BR(1)),ti(BR(end))],[2/3,1],tt(BR(1:end-1)))];colormap(hsv(1024)); %利⽤hsv的colormap填充彩⾊的⾊度图surf([xi;ones(size(xi))/3],[yi;ones(size(xi))/3],zeros(2,size(xi,2)),H,'edgecolor','none'); hold on;plot([0 1 0 0],[0 0 1 0],'linewidth',1,'color',[0.8 0.8 0.8]);%画三⾓plot(xi,yi,'k','linewidth',1);%画边缘hold off;grid on;axis equal;axis([-0.1 1 -0.1 1]);set(gca,'XTick',0:0.1:1,'Ytick',0:0.1:1);。
一、顏色之表示-色度圖(Chromaticity Diagram)在日常生活中我們會說幫我買「紅」色衣服,以工程背景的人會疑惑的反問是哪種「紅」?聖誕紅?粉紅?桃紅?)方向代表紅、橙、黃、朱紅?淡紅?深紅?所以人們用孟塞爾的色度圖,利用三度空間(圓柱座標)(見圖1)以角度(綠…等不同顏色色調(Hue),而以距離(r)表示彩度或純度(以C表示),高度代表明亮度(用V表示),H V/C表示一個顏色。
例如作為計算演色係數之色票5Y 6/4即色調H為5Y(即介於黃色10Y與紅黃色10YR之中間色)、亮度為6、飽和度為4之一個顏色。
這個用於印刷染料界很廣,但對於學工程最普遍的說法是,以一個顏色系統當作座標,你告訴我一個之色座標,則每一個人均可精確的理解你要的是什麼顏色。
顏色係人眼睛內之L,M,S錐狀體作用而形成,故人眼對顏色反應(類似於系統之脈衝響應),必須先探討,就像一個二極體對電壓、電流之特性參數,為了要取得這些參數必須做一連串之實驗以獲得相關之參數。
同樣地,人眼對R、G、B色之反應如何,也必須做一連串之配色實驗(color matching experiment),透過這些實驗來得到人眼對不同波長之反應參數,利用人眼對不同顏色之波長的反應,可將一個顏色對應到一個座標,而用座標表示顏色。
【圖1】Munsell 色度圖For personal use only in study and research; not for commercial use二、加法混光配色實驗人眼在中心窩︒2內光的加法(含亮度)成立,而加法混光意味著加法必須成立,也就是格拉斯曼定理(Grassman’s law)要成立即:For personal use only in study and research; not for commercial use-對稱性: U=V ó V=U -遞移性: U=V 和 V=W => U=W -比例性: U=V ó tU=tVFor personal use only in study and research; not for commercial use-疊加性: 若以下敘述中的任意兩個成立:U=V, W=X (U+W)=(V+X) 則第三個敘述必成立。
這些論述的真實性與任何生物學上定律的真實性是一樣的,說明了色彩疊加時是以線性的方式相加,這限制在視場︒2內。
在︒2內只有在錐形體沒有對光很靈敏桿狀體,故Grassman ’s law 成立。
通過了加法混色成立,我們才可以做下面的色匹配實驗(color matching experiment)。
1931年,國際照明委員會(CIE , Commission Internationale de L ’Eclairage)利用R λ=700.00nm(深紅)、G λ=546.1nm(黃綠色) 、B λ=435.8nm(帶紫藍色)之單色光(明度分別為1、4.59、0.06流明)當作三原色之色刺激(primary stimulus)。
用10人配色實驗(如下圖2),例如某一顏色的試驗光,照射在左側,而三個R 、G 、B 光(亮度分別為r 、g 、b)混合光投射在右側,此兩束光(測試光與混合光)交互左右兩側即閃爍法。
若觀察者覺得二者明顯不同(有色差、亮差)則表示尚未匹配,故調整r 、g 、b 重複上述閃爍試驗,一直到觀察者覺沒有變化稱匹配。
此時表示此測試光[][][][]B B G G R R F ++=。
【圖2】配色實驗(1)圖3(a)中,[]R 、[]G 、[]B 之三亮度為零,故右側呈現黑色。
適當調整R 、G 、B 量如圖3(b)仍與[]F 光不匹配,再做適當調整成圖3(c),則與F 光匹配,得[][][][]B B G G R R F ++=,其中三個純量R 、G 、B 均為正值,然在圖3(d)左側之[]F 光,無論用多少之R 、G 、B 均無法混成,如圖3(e) 所示。
但若將[]G 光與[]F 光混放在左側則得如圖3(f)之匹配光,即[][][][]B B R R G G F +=+或[][][][]B B G G R R F +-=,這也形成有負號之量。
因此通過實驗可以了解,幾乎任何顏色均可以用特定的三原合而成。
對於光譜的顏色,如波長為λ,頻帶寬為λ∆之顏色,同樣亦可用三原色混合而成。
若某單色光[]F 利用向量方式以三原色B G R,,,混合匹配時可得[][][][]G B G G R R F ++= 將可見光(380nm~780nm)以每10nm 分割,以380+10inm ,i=0,1,……,39當作試驗光重複在上述試驗,例如以10nm 為一個間隔,每一個單色光(即顏色為100%飽和之光)的匹配方程式:B b G g R r F380380380380++= B b G g R r F390390390390++=B b G g R r F 400400400400++=B b G g R r F780780780780++=,因此就可以得到三個匹配量之函數()λr 、()λg 、()λb ,稱為匹配函數(color matching function, CMF)。
(a)(b)(C)(d)(e)(f)【圖3】配色實驗(2)1931年Guild與Wright提出的10人觀測數值的平均值()λr、()λg、()λb,這個色匹配函數之平均值可認為是正常色視覺者的平均值,如圖4所示。
這個CMF可視為人眼對色彩的脈衝響應函數(impulse response)。
各個R,G,B視為單位向量構成三度空間之軸,使得任意一個顏色[F]為此三度空間上之一點,故為色空間(color space)。
【圖4】色匹配函數三、CIE色度圖因三度空間比較麻煩,同時透過加法混色()[]()[]()[]BbGgRrFλλλ++=,我們得知光顏色產生與三原色[]R、[]G、[]B之比例量有關與絕對值()λr、()λg、()λb無關,也就是另一色光其三分量為()λr a、()λg a、()λb a,此二個光之顏色對人眼而言只是亮度不一樣而顏色一樣。
故將()λr、()λg、()λb正規化求得相對值如下:)()()()()(λλλλλb g r r r ++= ())()()()(λλλλλb g r g g ++=())()()()(λλλλλb g r b b ++=,其中()()()1=++λλλb g r 。
所有單色光在 (r,g)-色度圖的形成之軌跡稱為光譜軌跡(Spectrum locus)如圖5。
其中三個原色光標示為R 、G 、B ,分別為[R]=700nm 、[G]=546.1nm 、[B]=435.8nm ,這些三原色光均實際上是存在的。
其中光譜軌跡因為單色光所連接之點所得曲線,如圖5之最外曲線(從380nm 至780nm ,為飽和度100%),故任意座標點超出此曲線,表示其飽和度超過100%均無意義的。
如上所述,RGB 表色系統的配色函數帶有負值。
因為負值的存在會造成運算的複雜性,於是為了(1)方便性和(2)只利用一個刺激值表示亮度,故CIE 於1931年在制定RGB 色度系統的同時,又確定了新的原刺激值[]X 、[]Y 、[]Z ,得到了XYZ 色度系統。
XYZ 表色系統也稱為CIE 1931表色系統(CIE 1931 standard colorimetric system)。
【圖5】(r,g)-色度圖CIE-RGB與CIE-XYZ變化,是利用圖5中,將落再第二象限有負座標全部右移,但所圈之面積只要把單色光光軌跡圖包括進去即可,不用太大之範圍,其原因如前述在單色光軌跡外面之座標點均無意義。
同時希望在新的座標系統中,只有一個刺激值Y代表亮度,而不像CIE-RGB系統中R,G,B之值均對亮度有貢獻,所以選定圖6(a)中,X與Z之連線為零亮度曲線。
而形成新的色度圖如圖6(b)所示,其X,Y,Z即代表再新色度圖的三原色。
這三個原色是不存在為虛擬的,所以CIE-XYZ之色度圖如圖6(b)所示,是唯一個虛擬但很方便的色度圖。
(a)CIE-RGB系統(b) CIE-XYZ系統【圖6】CIE之兩種色度圖原來之圖4含有負值之色匹配函數成為圖7全部為正值之色匹配函數。
一個色刺激例如光或一個反射物對人眼產生之三刺激值可由色匹配函數()λx ,()λy ,()λz 用下列式求出。
()()()()()()⎰⎰⎰⋅=⋅=⋅=vis vis visd z k Z d y k Y d x k X λλλφλλλφλλλφ其中k 為常數,積分⎰vis 取可見光波長區域。
【圖7】XYZ 色度系統之色匹配函數對於物體的色刺激,例如反射物體為()()()λλλφP R ⋅=,透射物體為()()()λλλφP T ⋅=。
其中()λP 為照明光的光譜分佈;()λR 為反射物體的光譜反射率; ()λT 為透射物體的光譜透過率。
因此,例如反射物體的三刺激值X,Y,Z 為()()()()()()()()()⎰⎰⎰⋅⋅=⋅⋅=⋅⋅=vis vis visd z P R k Z d y P R k Y d x P R k X λλλλλλλλλλλλ這裡假設k 為()()λλλd y p k vis⋅=⎰100常數k 的選擇是使完全反射(()1=λR )的三刺激值Y =100。
和前述的GRB 色度系統相同因為三刺激值X,Y,Z ,如考慮其向量的組成,在幾何學上的表示是需要使用三次元空間,我們把這種空間稱為色彩空間。
但是,三次空間的表示有不便之處,因此我們根據下公式Z Y X Yy ZY X X x ++=++=利用上式得到的x,y 稱為色的色座標。
一些CIE 標準光源之色座標如圖8所示。
【圖8】1931 CIE 色度圖(from )CIE-xy 色度圖最大功用在於色匹配(color matching)以及加法混色。
在圖9之色度圖中有一些重要資訊如:․E orE W (Equal Energy) 表等能量白光(i.e. x=1/3,y=1/3)。
․主波長:一個光源之色座標(x,y) 可分解為E W 白光與頻譜軌跡上之單色光波長為d λ即為混光之結果,即為此光源之主波長。
․純度(飽和度):光源 (x,y)愈接近頻譜軌跡表示愈純,純度=bEaE,其中aE為a點與E點之長,bE為b點到E點之長。
․一個紅光LED其x=0.67,y=0.27很接近頻譜軌跡故飽和度高。
․兩光源p點與q點之連線中之任一點表示此二光源混光之結果。
【圖9】在CIE1931色度圖做加法混光若在一顯示器如LCD或CRT,其最大紅光、綠光與藍光之色座標如圖10所示。