PI值计算方法1

详解各种随机算法之前将的算法都是确定的，即对于相同的输⼊总对应着相同的输出。

但实际中也常常⽤到不确定的算法，⽐如随机数⽣成算法，算法的结果是不确定的，我们称这种算法为（随机）概率算法，分为如下四类：1、数值概率算法⽤于数值问题的求解，通常是近似解2、蒙特卡洛算法Monte Carlo能得到问题的⼀个解，但不⼀定是正确解，正确的概率依赖于算法运⾏的时间，算法所⽤的时间越多，正确的概率也越⾼。

求问题的准确解；3、拉斯维加斯算法 Las Vegas不断调⽤随机算法求解，直到求得正确解或调⽤次数达到某个阈值。

所以，如果能得到解，⼀定是正确解。

4、舍伍德算法 Sherwood利⽤随机算法改造已有算法，使得算法的性能尽量与输⼊数据⽆关，即平滑算法的性能。

它总能求得问题的⼀个解，且求得的解总是正确的。

随机数概述计算机产⽣的随机数都是伪随机数，通过线性同余法得到。

⽅法：产⽣随机序列d称为种⼦；m取值越⼤越好；m，b互质，常取b为质数；案例伪随机数在实际编程中，我们使⽤rand()函数来产⽣随机数，rand()函数返回0到⼀个最⼤值之间的⼀个随机数。

#include#include#include//产⽣[0,100)的随机数void GenerateRandomNumber(){for(int i=0;i10;i++){printf('%-4d',rand()%100);//产⽣[0,m)的随机数}printf('\n');}int main(){GenerateRandomNumber();return 0;}运⾏代码，输出：41 67 34 0 69 24 78 58 62 64如果我们重复运⾏代码就会发现，每次的输出结果都是这个序列。

这就是因为rand产⽣的随机序列是伪随机序列。

解决⽅法是：使⽤当前的时间作为随机种⼦。

时间作为随机种⼦在GenerateRandomNumber()函数开头加⼊下⾯⼀条语句。

算法之美--1.蒙特卡洛⽅法计算pi基本思想：利⽤圆与其外接正⽅形⾯积之⽐为pi/4的关系，通过产⽣⼤量均匀分布的⼆维点，计算落在单位圆和单位正⽅形的数量之⽐再乘以4便得到pi的近似值。

样本点越多，计算出的数据将会越接近真识的pi（前提时样本是“真正的”随机分布）。

蒙特卡罗（Monte Carlo）计算圆周率的主要思想：给定边长为R的正⽅形，画其内切圆，然后在正⽅形内随机打点，设点落在圆内的概为P，则根据概率学原理： P = 圆⾯积 / 正⽅形⾯积＝ PI * R * R / 2R * 2R = PI / 4。

即 PI=4P。

这样，当随机打点⾜够多时，统计出来的概率就⾮常接近于PI的四分之⼀了。

#include <iostream>#include <ctime>using namespace std;int main(){const int MAX_TIMES = 20000000;srand(static_cast<unsigned int>(time(0)));int in=0;for (int i = 0; i < MAX_TIMES;i++){double x = static_cast<double>(rand()) / RAND_MAX;double y = static_cast<double>(rand()) / RAND_MAX;if (x*x+y*y<=1.0){in++;}if (i%(MAX_TIMES/100)==0){cout << ".";}}double pi = 4.0*in / MAX_TIMES;cout << "\nPI=" << pi << endl;return0;}实现了⼀下，感觉时间⽤的有点长。

TCD正常频谱图像分析1、频谱为一近似直角三角形，S1峰S2峰。

S2峰后有切迹，切迹之后为一明显D峰。

2、眼动脉（OA）高阻波形即有一个舒张期流速及舒张末期流速值均较低。

PI,RI,S/D均较高（外周血管）。

3、颅内血管均低阻波形。

即有一个较高舒张期流速及舒张末期流速值。

PI,RI,S/D均较低。

4、频宽基本相同，频窗明显。

异常TCD频谱图像一、血流速度收缩峰血流速度（Vp）平均血流速度（Vm）1、高阻波形（外周血管频谱图像）：低舒张末期流速→0。

PI↑、RI↑、S/D↑–意义：脑动脉硬化。

2、弥散型波形：频窗消失，包络线紊乱不规则，整个频谱弥散状。

–意义：轻-中度血管狭窄及动静脉畸形。

3、涡流：正常频谱的反向出现高强度的信号，一般均在收缩期出现。

–意义：明显的血管狭窄。

二、搏动指数（pulastility Index，PI）1、计算方法：PI=（收缩峰速度-舒张末速度）/平均速度=（Vp-Vp’）/Vm2、正常值：PI=0.6~1.053、意义：反映血管顺应性和血管弹性指标。

PI↑舒张末期血流速度降低所至，见于脑动脉硬化。

PI↓收缩期血流速度增加所至，见于脑血管畸形（A-V）、动脉瘤。

三、阻力指数(resistance Index RI)1、计算方法：RI=（收缩峰速度-舒张末速度）/收缩峰速度=（Vp-Vp’）/Vp2、正常值：RI=0.50~0.803、意义：反映血管的舒缩状况、阻力状况的指数。

四、收缩峰速度与舒张末速度的比值（S/D）1、计算方法：S/D=收缩峰速度/舒张末速度2、正常值：S/D>33、意义：评价血管顺应性和弹性的一个指标。

S/D↑见于脑动脉硬化TCD异常结果的临床意义一、血流方向异常1、MCA：表明颈内动脉或大脑中动脉梗塞的可能。

2、ACV：大脑前动脉梗塞或颈内动脉的严重狭窄或梗塞。

3、V A：可能有锁骨下动脉盗血。

二、血流速度异常1、收缩期血流速度（Vp）值增高。

什么是PID—一种通俗易懂的讲解来源：作者：时间：2008-01-15 点击：371最近从网上看到了一种对PID的解释，比较通俗易懂，也好记住，经过自己的整理后说明如下。

控制模型：你控制一个人让他以PID控制的方式走110步后停下。

（1）P比例控制，就是让他走110步，他按照一定的步伐走到一百零几步（如108步）或100多步（如112步）就停了。

说明：P比例控制是一种最简单的控制方式。

其控制器的输出与输入误差信号成比例关系。

当仅有比例控制时系统输出存在稳态误差（Steady-state error）。

（2）PI积分控制，就是他按照一定的步伐走到112步然后回头接着走，走到108步位置时，然后又回头向110步位置走。

在110步位置处来回晃几次，最后停在110步的位置。

说明：在积分I控制中，控制器的输出与输入误差信号的积分成正比关系。

对一个自动控制系统，如果在进入稳态后存在稳态误差，则称这个控制系统是有稳态误差的或简称有差系统（System with Steady-state Error）。

为了消除稳态误差，在控制器中必须引入“积分项”。

积分项对误差取决于时间的积分，随着时间的增加，积分项会增大。

这样，即便误差很小，积分项也会随着时间的增加而加大，它推动控制器的输出增大使稳态误差进一步减小，直到等于零。

因此，比例+积分（PI）控制器，可以使系统在进入稳态后无稳态误差。

（3）PD微分控制，就是他按照一定的步伐走到一百零几步后，再慢慢地向110步的位置靠近，如果最后能精确停在110步的位置，就是无静差控制；如果停在110步附近（如109步或111步位置），就是有静差控制。

说明：在微分控制D中，控制器的输出与输入误差信号的微分（即误差的变化率）成正比关系。

自动控制系统在克服误差的调节过程中可能会出现振荡甚至失稳，其原因是由于存在有较大惯性组件（环节）或有滞后（delay）组件，具有抑制误差的作用，其变化总是落后于误差的变化。

韦达圆周率公式(一)韦达圆周率公式引言韦达圆周率公式是由德国数学家韦达于欧洲文艺复兴时期发现的一条重要公式，它用于计算圆周率（π）的近似值。

韦达圆周率公式是数学中的经典问题之一，也是数学和计算机科学中的热门研究领域之一。

公式表达韦达圆周率公式可以用以下数学公式表示：π = 4/1 - 4/3 + 4/5 - 4/7 + 4/9 - 4/11 + …解释说明韦达圆周率公式的表达式中，每一项都是按照一定的规律进行交替相加或相减的。

公式中的每一项都是以4作为系数，然后分子是一个递增的奇数序列，分母是一个递增的偶数序列。

例如，公式中的第一项为4/1，第二项为-4/3，第三项为4/5，以此类推。

我们可以看出，随着项数的增加，每一项的绝对值越来越接近0，所以公式可以逼近圆周率π的值。

应用示例我们可以通过计算公式的前n项和，来近似计算圆周率π的值。

下面是一个计算π的示例：def calculate_pi(n):pi = 0sign = 1denominator = 1for i in range(n):term = 4 * sign / denominatorpi += termsign *= -1denominator += 2return piprint(calculate_pi在上述示例中，我们定义了一个函数calculate_pi来计算π的值。

函数的参数n表示要计算的公式项数。

我们使用循环来计算公式的前n项和，并将每一项累加到变量pi中。

最后返回pi即可。

当我们调用calculate_pi时，将会计算公式的前10000项和，并返回近似值。

根据实际运行结果，计算得到的近似值约为，与π的真实值非常接近。

总结韦达圆周率公式是一条重要的数学公式，用于近似计算圆周率π的值。

通过不断增加公式的项数，我们可以得到更精确的近似值。

这个公式在数学和计算机科学领域中有着广泛的应用和研究价值。

PI值计算方法1
PI值计算方法1
计算圆周率（π）的方法有很多种，下面介绍一种常见的方法。

第一种方法是通过蒙特卡洛方法计算圆周率。

蒙特卡洛方法是一种以概率为基础的计算方法，它通过随机模拟的方法来估计数值。

具体步骤如下：
1.在一个边长为1的正方形内，画一个与正方形边长相等的圆。

2.假设圆的半径为r，则圆的面积为π*r^2
3.在正方形内，随机生成n个点。

这些点均匀地分布在正方形内。

4.计算这n个点中落在圆内的点的个数，假设为m。

5.通过以下公式估计圆周率的值：π≈4*m/n。

这种方法的原理是，当n趋近于无穷大时，随机生成的点在正方形内的分布趋向于均匀分布，从而落在圆内的点的个数与总点数的比例近似等于圆的面积与正方形的面积的比例，即π/4、因此，通过计算这个比例的4倍即可估计出圆周率的值。

这种方法的优点是简单易懂，不需要复杂的计算和公式，只需要随机生成点并计算落在圆内的点的个数即可。

缺点是精度相对较低，需要生成大量的点才能得到较为接近真实值的估计结果。

为了提高精度，可以增加生成的点的数量，或者多次进行模拟并求取平均值。

总的来说，蒙特卡洛方法是一种利用随机性和概率的方法来估计数值的方法，可以广泛应用于数学、物理、金融等领域的计算和模拟中。

在计算圆周率时，通过大量的随机生成点并计算落在圆内的点的个数，可以得到圆周率的估计值。

虽然精度相对较低，但是通过增加点的数量或者进行多次模拟可以提高结果的准确度。

低压电缆头工作量计算公式在电力行业中，低压电缆头的工作量计算是非常重要的，它可以帮助工程师和技术人员准确地评估电缆头的负荷能力和使用寿命。

通过合理的工作量计算，可以有效地预防电缆头的过载和损坏，保障电力系统的稳定运行。

本文将介绍低压电缆头工作量计算的公式和方法。

低压电缆头的工作量计算公式通常包括以下几个关键参数：电流负荷、电压、线路长度、环境温度等。

根据这些参数，可以通过以下公式计算低压电缆头的工作量：P = I^2 R。

其中，P代表电缆头的功率损耗，单位为瓦特（W）；I代表电流负荷，单位为安培（A）；R代表电缆头的电阻，单位为欧姆（Ω）。

通过这个公式，可以清晰地计算出电缆头在特定工作条件下的功率损耗，从而评估其工作能力和使用寿命。

在实际工程中，工作量的计算还需要考虑到环境温度、线路长度、电压降等因素。

这些因素会对电缆头的工作性能产生影响，因此需要进行修正计算。

一般来说，可以通过以下公式进行修正计算：P' = P (1 + α (T T0))。

其中，P'代表修正后的功率损耗；α代表温度系数；T代表实际环境温度，单位为摄氏度（℃）；T0代表标准环境温度，一般取为20℃。

通过这个修正公式，可以根据实际环境温度对电缆头的功率损耗进行修正，从而更准确地评估其工作能力。

除了环境温度，线路长度和电压降也是影响电缆头工作量的重要因素。

一般来说，线路长度越长，电压降越大，电缆头的功率损耗也会相应增加。

因此，在实际工作量计算中，需要根据线路长度和电压降进行修正计算，以获得更准确的结果。

综上所述，低压电缆头的工作量计算公式包括了功率损耗的基本计算公式和修正计算公式。

通过这些公式，可以根据电流负荷、环境温度、线路长度、电压降等参数，准确地评估电缆头的工作能力和使用寿命，为电力系统的设计和运行提供重要参考。

在实际工程中，工作量计算是非常复杂和繁琐的工作，需要充分考虑各种因素的影响，并进行准确的计算和分析。

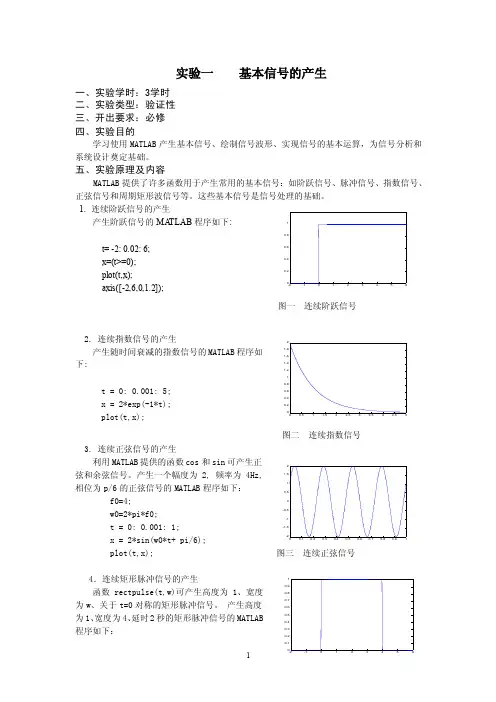
实验一 基本信号的产生一、实验学时：3学时 二、实验类型：验证性 三、开出要求：必修 四、实验目的学习使用MATLAB 产生基本信号、绘制信号波形、实现信号的基本运算，为信号分析和系统设计奠定基础。

五、实验原理及内容MATLAB 提供了许多函数用于产生常用的基本信号：如阶跃信号、脉冲信号、指数信号、正弦信号和周期矩形波信号等。

这些基本信号是信号处理的基础。

1. 连续阶跃信号的产生产生阶跃信号的MA TLAB 程序如下:t= -2: 0.02: 6; x=(t>=0); plot(t,x); axis([-2,6,0,1.2]);图一 连续阶跃信号2. 连续指数信号的产生产生随时间衰减的指数信号的MATLAB 程序如下:t = 0: 0.001: 5; x = 2*exp(-1*t); plot(t,x);图二 连续指数信号 3. 连续正弦信号的产生利用MATLAB 提供的函数cos 和sin 可产生正弦和余弦信号。

产生一个幅度为2, 频率为4Hz, 相位为p/6的正弦信号的MATLAB 程序如下：f0=4;w0=2*pi*f0;t = 0: 0.001: 1;x = 2*sin(w0*t+ pi/6);plot(t,x); 图三 连续正弦信号4．连续矩形脉冲信号的产生函数rectpulse(t,w)可产生高度为1、宽度为w 、关于t=0对称的矩形脉冲信号。

产生高度为1、宽度为4、延时2秒的矩形脉冲信号的MATLAB 程序如下：t=-2: 0.02: 6;x=rectpuls(t-2,4);plot(t,x); 图四 连续矩形脉冲信号5. 连续周期矩形波信号的产生函数square(w0*t)产生基本频率为w0 (周期T=2p/w0)的周期矩形波信号。

函数square(w0*t, DUTY)产生基本频率为w0 (周期T=2p/w0)、占空比DUTY= t/T*100的周期矩形波。

τ为一个周期中信号为正的时间长度。

什么是极化指数
一、极化指数（PI）和绝缘吸收比（DAR）
绝缘体对温度和湿度的变化很敏感。

测量开始可能会由于干扰电流的存在而不准确。

为了消除这些影响，有必要进行较长时间的测量并计算PI和DAR系数。

这些计算用于鉴定绝缘体的质量和老化问题。

用1分钟和10分钟时的绝缘电阻值计算PI、用30秒和60秒的绝缘电阻值计算DAR 的是仪器编程的默认值。

这些值可以在中被修改，以便适用不同的标准或一些特殊应用。

PI=R10mn/R1mn* DAR=R60s/R30s 绝缘体质量
<1 <1.25 危险
1-2 <1.25 不足
4 1.25-1.6 良好
>4 >1.6 很好
极化指数
极化指数PI：在同一次试验中，加压10min时的绝缘电阻值与加压1min时的绝缘电阻值之比。

《国家电网山东电力集团公司2007版电力设备交接和预防性试验规程》对极化指数有如下规定：极化指数在常温下不低于1.5；当R60s大于10000MΩ时，极化指数可不作要求。

预试时可不测量极化指数；吸收比不合格时增加测量极化指数，二者之一满足要求即可。

《电气装置安装工程电气设备交接试验标准》（GB 50150-2006），7.0.9第4条，变压器电压等级为220kV及以上且容量为120MVA及以上时，宜用5000V兆欧表测量极化指数。

测得值与产品出厂值相比应无明显差别，在常温下不小于1.3；当R60s大于10000MΩ时，极化指数可不做考核要求。

浙江大学城市学院实验报告课程名称多核与并行程序设计实验项目名称实验五蒙特卡罗法求PI及排序算法学生姓名专业班级学号实验成绩指导老师（签名）日期【实验环境】硬件平台：联想4核,4GZ内存编译器：Microsoft Visual Studio C++ 6.0操作系统：Windows 2003 server sp2测试数据集合：由随机数函数产生的数据集合【实验1】一、问题描述蒙特卡洛算法可理解为通过大量实验，模拟实际行为，来收集统计数据。

本例中，算法随机产生一系列点，模拟这些点落在如下图所示的正方形区域内的情况。

其几何解释如下11图1如图1所示，正方形边长为1，左下顶点与原点重合，两边分别与x，y轴重合。

曲线为1/4圆弧，圆心位于原点，与正方形左下定点重合，半径为1。

正方形面积S1=1，圆弧内面积S2=ππ41412=r。

算法模拟大量点随机落在此正方形区域内，落在圆弧内的点的数量（n2）与点的总数（n1）的比例与面积成正比关系。

即π42121==S S n n （1） 由此可得124n n =π （2）因此，只要计算出落在圆弧内的点的数量在点总数中所占的比例，就能求出π的值。

由图1可知，所有点均落在正方形范围内，因此点的x 坐标满足10≤≤x 。

又，当点落在圆弧范围内，则点的二维坐标关系满足122≤+y x 。

检验每一个点是否满足此关系即可判定改点是否落在圆弧内。

二、串行算法描述本项目中使用了标准C 语言库中的产生随机数函数。

该函数原型为：int rand( void );此函数产生随机数列，每次调用时均返回0到RAND_MAX 之间的一个整数。

void srand( unsigned int seed );此函数为rand （）函数所生成的伪随机数序列设置起始点，使之产生不同的伪随机数。

算法：产生2n 个随机数据，范围[0，1]，对每个数据点计算其坐标是否满足122≤+y x ，统计满足此关系的点的数量count ，则 n count4=π三、并行算法3.1 并行算法描述算法步骤：1、确定需要产生的点的个数n ，参与运行的处理器数m ；2、对每一个处理器，生成两个随机数x ，y ，范围[0，1]；3、判断两个随机数x ，y 是否满足122≤+y x ；4、若满足，则变量COUNT i++；5、重复步骤2-4，直至每个处理器均生成n/m个随机点；6、收集COUNT i的值，并累加至变量COUNT中，此即为随机点落在圆弧内的数量；7、通过（2）式计算 的值。

血氧仪上的pi值
血氧仪上的pi值
血氧仪是一种常用的医疗仪器，它可以检测人体血氧饱和度（SpO2）和脉率（PR）。

它以标准值90%-100%的血氧饱和度和60-100次/分的脉率为基础，可以帮助医生准确判断患者的血氧状态。

血氧仪上的pi值是指血氧值的国际标准。

它由两部分组成，一部分是血氧饱和度，另一部分是脉率。

pi值是血氧值标准的一种综合评分，表示患者的血氧状态，该值越高，表示患者的血氧状态越好。

pi值可以帮助医生更好地评估患者的血氧状态，是血氧仪的一个重要指标。

pi值的正常范围为90-100，如果pi值低于90，表明血氧水平不正常，患者可能出现低氧症状，需要更加注意，及时采取措施改善血氧水平。

总而言之，pi值是血氧仪的一个重要指标，它可以帮助医生评估患者的血氧状态，pi值的正常范围为90-100，如果pi值低于90，表明血氧水平不正常，患者可能出现低氧症状，应及时采取措施改善血氧水平。

2008年西医综合强化班辅导讲义----生物化学南方医科大学Dr.姜立 1第一章 蛋白质的结构与功能（一）蛋白质的基本组成单位是氨基酸编码氨基酸：自然界存在的氨基酸有300余种，构成人体蛋白质的氨基酸只有20种，且具有自己的遗传密码。

各种蛋白质的含氮量很接近，平均为16%，（二）氨基酸的分类：1．所有的氨基酸均为L型氨基酸（甘氨酸除外）2．根据侧链基团的结构和理化性质，20种编码氨基酸分为四类：3．含有硫原子的氨基酸：蛋氨酸（又称为甲硫氨酸）、半胱氨酸（含有由硫原子构成的巯基－SH）、胱氨酸（由两个半胱氨酸通过二硫键连接而成）4．芳香族氨基酸（按吸光度排列）：5．唯一的亚氨基酸：脯氨酸，其存在影响α-螺旋的形成6．营养必需氨基酸：7．出现的非编码氨基酸有：羟脯氨酸、羟赖氨酸、鸟氨酸、瓜氨酸、同型半胱氨酸、磺酸丙氨酸、5-羟色氨酸等（三）氨基酸的理化性质：1．氨基酸的两性解离性质：所有的氨基酸都含有能与质子结合成NH3＋的氨基；含有能与羟基结合成为COO－的羧基，因此，在水溶液中，它具有两性解离的特性。

在某一pH环境溶液中，氨基酸解离生成的阳离子及阴离子的趋势相同，成为兼性离子。

此时环境的pH值称为该氨基酸的等电点（pI），氨基酸带有的净电荷为零，在电场中不泳动。

pI值的计算如下：pI＝1/2（pK1 + pK2）,(pK1和pK2分别为α-羧基和α-氨基的解离常数的负对数值)2．氨基酸的紫外吸收性质：（1） 吸收波长：280nm（2） 结构特点：分子中含有共轭双键（3） 光谱吸收能力：色氨酸＞酪氨酸＞苯丙氨酸3．呈色反应：氨基酸与茚三酮水合物共加热，生成的蓝紫色化合物在570nm波长处有最大吸收峰；蓝紫色化合物＝（氨基酸加热分解的氨）+（茚三酮的还原产物）+（一分子茚三酮）（四）肽的相关概念1．寡 肽：小于10分子氨基酸组成的肽链2．多 肽：大于10分子氨基酸组成的肽链3．氨基酸残基：肽链中因脱水缩合而基团不全的氨基酸分子4．肽 键：连接两个氨基酸分子的酰胺键（－CO－NH－），包含C、O、N、H四个原子，在同一平面中5．肽单元：参与肽键的6个原子Cα1、C、O、N、H、Cα2位于同一平面，组成肽单元。

python中pi的用法(一)Python中pi的用法详解Python是一门强大而灵活的编程语言，它提供了许多有用的数学函数和常量，其中一个重要的常量是π（pi）。

在Python中，我们可以通过使用math模块来访问π的各种用法。

下面是一些常见的用法，供您参考：导入math模块为了使用π和其他数学函数，首先需要导入math模块。

可以使用以下代码将其导入Python程序：import math获取π的值要获取π的值，可以使用``。

以下是一个简单示例：import mathpi_value =print(pi_value)输出结果为：使用π进行数学计算π在数学计算中经常被使用。

下面是一些使用π进行数学计算的示例：计算圆的周长import mathradius = 5circumference = 2 * * radiusprint(circumference)输出结果为：计算圆的面积import mathradius = 5area = * radius**2print(area)输出结果为：利用π进行三角函数计算π在三角函数计算中扮演着重要的角色。

以下是一些使用π进行三角函数计算的示例：计算正弦值import mathangle = / 4sin_value = (angle)print(sin_value)输出结果为：计算余弦值import mathangle = / 3cos_value = (angle)print(cos_value)输出结果为：其他用法除了上述示例外，π还可以在许多其他场合使用，如统计学、物理学等。

Python的math模块提供了许多其他与π相关的函数和常量，您可以在需要时进行深入研究。

以上是关于在Python中使用π的一些常见用法的详细讲解。

希望本文对您有所帮助！使用π进行指数计算π可以用来进行指数计算，以下是一个示例：import mathexponential_value = ()print(exponential_value)输出结果为：利用π进行对数计算π可以用来进行对数计算，以下是一个示例：import mathlog_value = ()print(log_value)输出结果为：使用π进行数值比较π可以用来进行数值比较，以下是一个示例：import mathresult = >print(result)输出结果为：利用π进行随机数生成π可以用来进行随机数生成，以下是一个示例：import mathimport randomrandom_value = () *print(random_value)输出结果为：使用π进行三角函数反函数计算π可以用来进行三角函数反函数计算，以下是一个示例：import matharcsin_value = (1 / )print(arcsin_value)输出结果为：利用π进行单位转换π可以用来进行单位转换，例如将弧度转换为度，以下是一个示例：import mathradians = / 4degrees = (radians)print(degrees)输出结果为：以上是关于在Python中使用π的一些更多用法的详细讲解。

化简比并求比值计算过程比例是数学中重要的概念，它是用一个数与另一个数比较的关系。

比例是离散数与连续数关联的基础，在许多领域，比例都有着极为广泛的应用场景。

在本文中，我们将讨论如何化简比例及计算比值。

一、化简比例化简比例是指将分式中的分子与分母都乘以相同的常数，使得分式的值不变，但分式中的分子与分母都可以变为最简形式。

化简比例的步骤如下：1.将比例中分子与分母相同的同类项合并。

2.提取比例中的公因数。

3.将比例中的分式进行约分，使分数化简为最简形式。

例如，将比例$\frac{12}{18}: \frac{24}{9}$化简，步骤如下：①将分式中的分子与分母相同的同类项合并，得到：$\frac{4}{6}: \frac{8}{3}$②提取比例中的公因数，得到：$\frac{4}{6}: \frac{8}{3} = \frac{4}{6}\cdot\frac{1}{4}: \frac{8}{3}\cdot\frac{1}{4} = \frac{1}{3}: \frac{2}{3}$③将比例中的分式进行约分，得到：$\frac{1}{3}: \frac{2}{3} = \frac{1}{2}$因此，比例$\frac{12}{18}: \frac{24}{9}$的最简形式为$\frac{1}{2}$。

二、求比值在数学中，比值是指两个数的比例，其表示为a:b或a/b。

计算比值时，需要首先了解比例的含义并将其化简为最简形式，然后将比例中的分子与分母相除，得到比值。

例如，将比例$\frac{\pi}{2}:\frac{20}{\pi}$求比值，步骤如下：①将比例中分子与分母相同的同类项合并，得到：$\frac{\pi^2}{40}$②将比例中的分式进行约分，得到：$\frac{\pi^2}{40\pi^2}$③将比例中的分子与分母相除，得到比值：$\frac{\pi^2}{40\pi^2} = \frac{1}{40}$因此，比例$\frac{\pi}{2}:\frac{20}{\pi}$的比值为$\frac{1}{40}$。

血氧仪上的pi%正常值
血氧饱和度指数（Pi%）是一个用于评估身体可以利用氧气的能力。

它是血液中氧气
与血液中其他气体混合物含量之差除以血液中其他气体混合物含量再乘以100，表示血液
可以利用氧气的能力，以百分之一来度量。

正常人舌上吮吸试纸产生的血氧饱和度指数（Pi%）正常值大约在97%到99%之间，如
果血氧饱和度指数低于这个值就说明出现了氧气不足的情况。

通常来说，血氧饱和度指数
在90%以下就属于严重缺氧。

一般情况下，血氧饱和度指数在90%到94%之间也可能是缺氧状态。

血氧饱和度反映身体对氧气利用的能力，它是有关患者身体氧气运动能力的重要指标。

血氧饱和度指数低于正常值时，会出现氧气不足（hypoxia），这时候会出现呼吸急促、
心悸和昏厥等症状，如果持续抗衰老，会有心血管系统实质性损伤的风险。

血氧饱和度得
到正常的控制是提高运动能力的关键，保持血氧饱和度在正常水平也是提高疾病抵抗能力
的必备条件之一。

因此，血氧饱和度指标是评估氧气运动能力以及预防各种慢性疾病的重要指标，为了
保证身体健康，一定要时刻注意血氧饱和度，并尽量保持在正常水平，从而保护自身健康。

幼儿pi值正常范围亲爱的家长们，您是否曾为孩子的成长指标而操心？是否好奇幼儿的pi 值到底在怎样的范围才算正常？今天咱们就来好好聊聊这个话题。

您知道吗？pi 值就像是孩子成长路上的一个小密码，它能反映出孩子身体发育的一些重要信息。

对于幼儿来说，pi 值的正常范围可不是随便定的。

这就好比咱们种庄稼，不同的种子在不同的土壤和气候条件下，有它适合生长的规律。

幼儿的成长也是一样，年龄不同，pi 值的范围也就不同。

比如说 1 岁的小宝贝，pi 值可能在某个特定的区间。

可您要是拿这个标准去衡量 3 岁的孩子，那可就不对啦！这就好像让小树苗和大树比谁更粗壮，根本不是一个阶段嘛！咱们再打个比方，pi 值就像是孩子的身高，随着年龄增长不断变化。

如果某个阶段的 pi 值不正常，那可能就像小树苗长歪了一样，得引起咱们的注意啦。

一般来说，1 - 2 岁的幼儿，pi 值通常处于一个相对较低的范围。

这个时候的宝宝，就像刚刚发芽的嫩苗，还在慢慢成长。

可到了3 - 4 岁，pi 值的范围就会有所提高，就像小嫩苗开始茁壮成长，变得更加强壮。

那家长们可能要问啦，这 pi 值到底是怎么测出来的呢？这可不是随便拿个尺子量一量就行的。

通常需要专业的医生，通过一系列科学的方法和仪器来检测。

要是发现孩子的 pi 值不在正常范围内，那可别慌！这不一定就意味着有大问题。

也许只是孩子这段时间营养没跟上，或者是运动量不够。

就像汽车没油了跑不快，加点油、保养保养就好啦。

但要是一直不正常，那可就得重视起来，找找原因。

是孩子挑食？还是身体有什么潜在的小毛病？这时候，家长可就是孩子的守护天使，得带着孩子及时去看医生，找到解决问题的办法。

所以啊，家长们要多关注孩子的成长，定期带孩子去做检查，了解孩子的 pi 值情况。

这就像给孩子的成长之路点亮一盏明灯，让咱们能更好地陪伴他们健康长大。

总之，幼儿的 pi 值正常范围是个重要的参考指标，咱们要重视但别过度紧张。

用爱和细心，为孩子的成长保驾护航！。