当前位置：文档之家 › 《管理运筹学》第3章--线性规划的对偶问题

《管理运筹学》第3章--线性规划的对偶问题

  • 格式：ppt
  • 大小：781.00 KB
  • 文档页数：36

下载文档原格式

  / 36

合集下载

第3章 线性规划的对偶理论

第3章 线性规划的对偶理论

第三章 线性规划的对偶理论内涵一致但从相反角度提出的一对问题互为对偶（Dual ）问题。

例如，我们可以问当四边形的周长一定时，什么形状的面积最大？答案当然是正方形；我们也可以这样来问，四边形的面积一定时，什么形状的周长最短？答案同样是正方形。

对偶现象相当普遍，它广泛地存在于数学、物理学、经济学等诸多领域。

每一个线性规划问题都有和它相伴随的另一个问题，一个问题称为原问题，则另一个则称为其对偶问题。

原问题与对偶问题有着非常密切的关系，以至于可以根据一个问题的最优解，得出另一个问题最优解的全部信息。

然而，对偶性质远不仅是一种奇妙的对应关系，它在理论和实践上都有着广泛的应用。

§1对偶问题的提出对偶理论是以对偶问题为基础的，研究对偶理论，首先必须讨论对偶问题的提出。

对偶问题可以从经济学和数学两个角度来提出，本教材仅限于从经济学角度提出对偶问题。

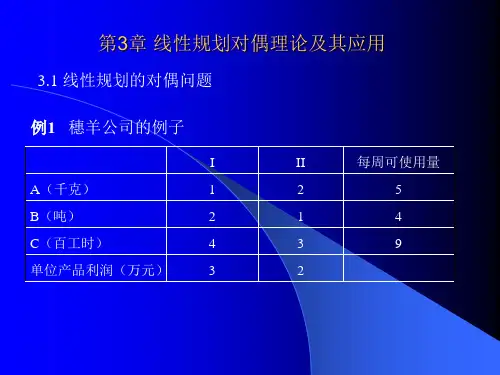
[例3-1] 构造例2-1的对偶问题我们已构造了例2-1追求最大利润的数学模型（见第6页），现在让我们从另外一个侧面来反映一下该问题。

倘若工厂有意放弃甲、乙两种产品的生产，而将其所拥有的资源转让出去；假设有一厂商要购买该工厂的三种资源，那么对三种资源的报价问题将成为关注的焦点。

设1y 、2y 和3y 分别代表厂商对A 、B 、C 三种资源的报价，那么站在厂商的立场上，该问题的数学模型又将是什么样子的呢？首先分析一下厂商购买所付出的代价32112168y y y w ++=。

自然，作为买方厂商当然是希望价格压得越低越好，因此厂商追求的应是付出代价的最小值，即：32112168min y y y w ++=然而，价格能否无限地压低呢？答案当然是否定的，因为最低报价必须以卖方能够接受为前提，否则报价再低也是没有意义的。

落实到这一问题上就是必须保证企业让出资源的收益不低于自己生产创造的利润，即：1y + 42y ≥ 221y +43y ≥ 31y ，2y ，3y ≥ 0至此我们得到了一个完整的线性规划模型：32112168min y y y w ++=1y + 42y ≥ 221y +43y ≥ 31y ，2y ，3y ≥ 0将站在厂商的立场上建立起来的数学模型同站在工厂立场上所建立的数学模型加以对比，可以发现它们的参数是一一对应的。

运筹学3对偶

运筹学3对偶

(LP) Max z = cT x s.t. Ax ≤ b x ≥0
(DP) Min f = bT y s.t. AT y ≥ c y ≥0
则（DP）称为（LP）的对称形式对偶问题
例3．2 写出下面线性规划的对偶规划模型
max 3 x1 75x 2 2 x3 x 4 2 x1 5 x 2 6 x3 x 4 40 3 x 2 x x x 50 1 2 3 4 x1 2 x 2 3 x3 2 x 4 20 x j 0, j 1,2,3,4
令 y1 =
y1’ - y1’’，于是有
min f b1 y1 b2 y2 bm ym a11 y1 a21 y2 am1 ym c1 a y a y a y c m2 m 2 12 1 22 2 a1n y1 a2 n y2 amn ym cn y2 ,, ym 0 y1没有非负限制
对偶定理
•定理 3.1 (对称性定理) 对偶问题的对偶就是原
问题。
•定理 3.2（弱对偶定理）设 X, Y分别是 P 和 D 的可行解，则 CTX bTY。 •证：由 P 和 D 的约束条件 AXb, ATYC, X0, y0 可直接推得 CTX YT AX YTb =bTY，证毕。
某工厂拥有A、B、C三种类型的原料，生 产甲、乙两种产品。每件产品在生产中消耗 的原料数量，每件产品的价格以及三种原料 可利用的数量如下表所示：
产品
原料 A
甲
1
乙
1
原料数量 （吨）
300
B C
价格（元/件）
2 0
50
1 2
100
400 250

线性规划[对偶问题](第3章2014.9)资料

线性规划[对偶问题](第3章2014.9)资料

对
原问题
对偶问题
偶
（MaxZ）
（MinS）
问
cj
bi
A
AT
题
约≤
正变量
及
束＝ 条≥
变 自由变量 量 负变量
其
件 m个
m个
数
正变量 约
≥
变 自由变量 束
=
学
量 负变量 条
≤
n个 件
n个
模
型
OR课件
§1 对 偶 问 题 及 其 数 学 模 型
LP
➢建立对偶问题？
➢方法一： 按程序先化为“一致性”形式，
OR课件
回
LP
➢对于所有的线性规划问题基本可以求解；
➢可以获得决策变量的信息、目标函数的信 息以及资源用完与否的信息等，如生产计划 问题。
顾
❖但是：
➢如何判断资源在规划中的重要程度？
➢有没有什么方法可以替代因“构造基”， 给LP问题求解带来的繁琐？
➢如何从LP问题的求解过程中获得更多 信息，以增强决策的准确性。
工
机
A
B
C
D
单位利润
器
时
（元）
产品
甲
2
1
4
0
2
乙
2
2
0
4
3
可供台时
1200
800
1600
1200
OR课件
§1 对 偶 问 题 及 其 数 学 模 型
LP
➢建模分析： ▪首先站在厂商的角度，如何安排生产， 使利润达最大？－－原问题 ▪然后站在承租人的角度，如何安排， 使成本达最小？－－对偶问题
OR课件
题

运筹学03线性规划对偶理论及其应用

运筹学03线性规划对偶理论及其应用

二、对偶单纯形法的计算步骤
1 ． 给定一个初始对偶可行的基本解，设相应的基为 B 。（此时单纯形 1 ． 给定一个初始对偶可行的基本解，设相应的基为 B 。（此时单纯形
表中的基本解必须满足最优检验，最小化问题检验数≥ 0 或最大化 表中的基本解必须满足最优检验，最小化问题检验数≥ 0 或最大化 问题检验数≤ 0 ） 问题检验数≤ 0 ）
定理3.3（最优性） 如果 x ， u 分别是原问题 minz=cx 和对偶问题 maxw=ub的可行解，且有ub cx，则x，u分别 是原问题和对偶问题的最优解。 定理3.4（强对偶性，即对偶定理） 若 原 问 题 minz=cx 有 最 优 解 x ， 则 对 偶 问 题 maxw=ub 也有最优解 y ，且目标函数值相等， 即 cx yb 。


定理3.1（对称性） 对偶问题的对偶问题就是原问题。即对偶问题与原 问题互为对偶问题。

定理3.2（弱对偶性） 如果x，u分别是原问题minz=cx和对偶问题 maxw=ub的可行解，则 ub cx 。
由弱对偶性得到的三个推论：
推论3.1 如果x*，u*分别是原问题minz=cx和对偶问 题maxw=ub的可行解，且cx*=u*b，则x*，u*分 别是原问题和对偶问题的最优解。 推论3.2 原问题和对偶问题有最优解的充分必要条件是它 们同时有可行解。 例：已知线性规划问题
min z x1 x 2 x1 x 2 1 x1 x 2 1 x 0， x 0 2 1
max w y1 y 2 y1 y 2 1 y1 y 2 1 y 0， y 0 2 1

* * 4 / 5, y2 3 / 5; z 5 已知其对偶问题的最优解为 y1 试用对偶理论找出原问题的最优解。

运筹学--线性规划的对偶理论

运筹学--线性规划的对偶理论


对偶单纯形法求解思路


对偶单纯形法
20
对偶单纯形法
21
对偶单纯形法

对偶单纯形法并不是所有线性规划问题的通用 解法，它只能从检验数已经符合最优化条件的 基本解开始求解。
22
对偶单纯形法

1- 约束条件为“≥”

初始解可以是非可行解。当检验数都为负数时，就 可以进行基变换，不需要加入人工变量。

2- 变量多于约束条件


对于变量多于约束条件的线性规划问题，用对偶单 纯形法计算可以减少计算工作量。 变量少，约束条件很多的线性规划问题，可以将其 变换为对偶问题，然后用对偶单纯形法求解。
23
对偶单纯形法示例1
24
对偶单纯形法示例1
25
对偶单纯形法示例1
26
灵敏度分析


线性规划问题的最优解，是在设定问题模型中 的������������������、������������、������������都为已知常数的前提下求解得到 的。 对于许多实际问题，这些系数都是采用经验法 或统计、预测方法得到的估计值。

这里需注意区分xi是最优表中的基变量还是非 基变量：

如果xi为非基变量，如产品C的原材料消耗系数pi发 生变化时，判断和求解的方法与前一种情况相同， 即检查xi的检验数是否满足最优条件；
59
灵敏度分析示例1

如果xi是基变量（例如产品A或产品B的资源消耗系 数p1或p2发生变化），那么p������的变化将引起基矩阵B 的变化。B的变化将影响单纯形法迭代过程中几乎 所有的计算项目，问题只能重新迭代。
32
灵敏度分析示例1
33

运筹学线性规划与对偶问题PPT.

运筹学线性规划与对偶问题PPT.

侮辱国歌案例
国歌是一个国家的象征，是国家的一种尊严和荣誉。

然而，近年来，一些人对
国歌的尊重和保护意识不足，甚至出现了侮辱国歌的行为。

这种行为不仅是对国家的不敬，更是对国家法律的挑衅。

下面我们就来看一些侮辱国歌的案例。

首先，我们可以看到一些人在公共场合对国歌进行恶搞、歪曲、改编，甚至以
恶搞的方式演唱国歌。

这种行为严重伤害了国歌的庄严形象，是对国家尊严的一种伤害。

国歌是国家的象征，任何对国歌的不敬都是对国家的不敬。

其次，一些人在社交媒体上散布侮辱国歌的言论和图片，甚至制作恶搞国歌的
视频。

这种行为不仅是对国歌的不尊重，更是对国家法律的挑衅。

国家有关法律法规对侮辱国歌的行为有明确的规定，任何人都不能违反国家法律。

最后，一些人在体育比赛等场合，对国歌进行了不尊重的行为，比如在国歌奏
响时不肃立、不肃静，甚至出现了一些人倒立、扭曲身体等不文明行为。

这种行为不仅是对国歌的不敬，更是对国家的不尊重和不礼貌。

总之，侮辱国歌的行为不仅是对国歌的不尊重，更是对国家的不敬和挑衅。

我
们每个人都应该尊重国歌，保护国歌，树立正确的国家荣誉感和民族自豪感。

同时，国家也应该加强对侮辱国歌行为的监管和处罚，让侮辱国歌的行为受到应有的惩罚，维护国家的尊严和形象。

希望全社会都能共同努力，共同维护国歌的尊严和荣誉，共同建设和谐美好的社会。

运筹学—线性规划对偶理论及其应用

运筹学—线性规划对偶理论及其应用
4
3
-1
-7
[-2]
基变量
3
2
0
0
0
b
CB
xB
x1
x2
x3
x4
x5
0
x3
0
5/4
1
0
-1/4
11/4
（1）+5*（3）/4
3
x1
1
3/4
0
0
1/4
9/4
（2）+3*（3）/4
0
x4
0
-1/2
0
1
-1/2
1/2
0
2
0
0
-1/3
-4/3
0
-7
继续迭代，并删除原第一列，得下表：
故新的最优生产计划是产品I、II分别生产1单位和2单位，总利润为7万元。
LP
DLP
3.2 对偶规划的基本性质
3.2.1 对称性定理：线性规划的对偶问题的对偶问题是原问题。
证明：
对偶定义
令w’=-w； 约束方程左右同乘“-1”
对偶定义
令z=-z’； 约束方程左右同乘“-1”
3.2 对偶规划的基本性质
3.2.2 弱对偶性定理： 如果X、Y分别是原问题和对偶问题的一个可行解，则其对应的原问题的目标函数值不大于对偶问题的目标函数值，也即
x5
x5
x6
0
x3
0
0
1
0
[-2]
2
-1
3
x1
1
0
0
0
-4/5
6/5
0
1
x2
0
1

第3章 管理运筹学线性规划问题的求解

第3章 管理运筹学线性规划问题的求解
总成本将由 800万 增 加到 804万。
？
若约束条件的
Min f = 2x1 + 3 x2 约束条件：
对偶价格小于 s.t. x1 + x2 ≥ 350 +1
0, 则其最优目
x1
≥ 125
标函数值受到 2 x1 + x2 ≤ 600
影响 (变坏) 。
x1 , x2 ≥ 0
§2 “管理运筹学”软件的输出信息分析
x1 , x2 ≥ 0
6
第三§步1：点“管击理“新运建筹”学按”钮软，输件入的数操据作。方法
2
3
例 1 中 共 有 2 个 变 量 ,3 个约束条件,目标函数 取 MAX. 点 击 “ 确 定 ” 。
例1. 目标函数：
Max z=50 x1+100x2 约束条件：
x1 + x2 ≤ 300 (1)
x2 ≤ 250 (3) x1 ≥ 0 x2 ≥ 0
14
相差值表示相应的决策变量的目标系数需要改 进的数量，使得决策变量为正值，当决策变量 已为正数时，相差数为零。
15
松弛/剩余变量的数值表示 还有多少资源没有被使用。 如果为零，则表示与之相对 应的资源已经全部用上。
例1. 目标函数：
Max z=50 x1+100x2 约束条件：
常数项范围是指约束条件
Max z=50 x1+100x2 约束条件：
的右端常量。上限值和下 限值是指当约束条件的右 端常量在此范围内变化时， 与其对应的约束条件的对 偶价格不变。当前值是指
x1 + x2 ≤ 300 2x1 + x2 ≤ 400
x2 ≤ 250 x1 , x2 ≥ 0

运筹学Chap3线性规划对偶理论及其应用

运筹学Chap3线性规划对偶理论及其应用

其对偶问题为
写成分量形式，即
max
2
1
u1 u2
1
1
s.t.
6
1
0
1
5
1 2 0
u1 u2
0
21
0
1
0
max 2u1 u2
u1 u2 5
s.t.6uu11
u2 2u2
0 21
u1
0
u2 0
模型对比(对称形式)
max Z 10 x1 18 x2
5 x1 2 x2 170
第三章
线性规划对偶理论及其应用
(Linear Dual)
教学要求：
掌握线性规划对偶理论及其基本经济学意义； 了解运用对偶理论对线性规划最优解进行分析的基本方法； 会运用对偶理论对一些基本的管理问题进行经济学分析。
目录
• 线性规划的对偶问题 • 对偶规划的基本性质 • 对偶单纯形法 • 影子价格和灵敏度分析
束。
线性规划问题的对偶问题（非对称）举例
写出下列线性规划
系数变成约束
先化为最小化问题： 条件右侧值
问题的对偶问题：
max z x1 x2 x3
x1 x2 2x3 25
xx11x,1x
2x2 x2 x3 2 0
x3 3
2
变成第一个约
束条件的系数
min z x1 x2 x3
x1 x2 2x3 25
x1 x1 x1
x2 x2 0,
x2
4 2
0
无界
关于无界性有如下结论：
minW 4 y1 2 y2
原问题
问题无界
无可 行解
对偶问题 无可行解 无可行解

管理运筹学-03-对偶问题与灵敏度分析3课件

管理运筹学-03-对偶问题与灵敏度分析3课件
管理运筹学
管理运筹学-03-对偶问题与灵敏度分析3
第三讲
对偶问题与灵敏度分析
管理运筹学-03-对偶问题与灵敏度分析3
对偶问题
2020/12/5
管理运筹学-03-对偶问题与灵敏度分析3
3
一、问题的提出
一般性的资源交易问题，见P70。
2020/12/5
管理运筹学-03-对偶问题与灵敏度分析3
4
二、对称形式下对偶问题的一般形式
11
2020/12/5
cj
3
2
2
CB
基
b
x1
x2
x3
0
x4
(b)
1
1
1
0
x5
15
(a)
1
2
0
x6
20
2
(c)
1
cj-zj
3
2
2
……
0
x4
5/4
0
0
(d)
3
x1
25/4
1
0
(e)
2
x2
5/2
0
1
(f)
cj-zj
0
(k)
(g)
0
0
0
x4
x5
x6
1
0
0
0
1
0
0
0
1
0
0
0
(l) -1/4 -1/4
0
3/4
(x1,x2,x3,x4,x5) (0,0,6,8,18) (0,/,0,/,/) (0,4,6,0,6) (0,6,6,-4,0) (6,0,0,8,6) (/,0,/,0,/) (9,0,-3,8,0) (6,4,0,0,-6) (6,2,0,4,0) (3,4,3,0,0)
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

x1 x2 x3 2
s.t.
x12x1x2
x3 x2
1 x3
2
x1 0; x2 , x3 ?
•
这样所有的约束条件均为“≤”和“=”类型，按前述对
应关系原则，可写出其对偶问题为：
minW ( y) 2 y1 y2 2 y3
y1 y2 2 y3 1
s.t.
y1 y1
y2 y2
min W ( y) 2 y1 6 y2 0 y3/ 0 y3//
y1
s.t.
0
y1
y1
2 y2 y3/ y3// 0
y2
y/ 3
y3/ /
2
6 y2 3 y3/ 3 y3//
5
y1
,
y2
,
y/ 3
,
y3/ /
0
13
OR:SM
• 再设y/3-y//3=y3，代入上述模型得：
始问题，则（3-2）称为对偶问题。
8
OR:SM
• 3.1.2 对称型线性规划问题——对称型对偶问题
•
• 每一个线性规划问题都必然有与之相伴随的对偶问题 存在。先讨论对称型对偶问题；对于非对称型对偶问题， 可以先转化为对称型，然后再进行分析，也可以直接从 非对称型进行分析。
• 对称型线性规划问题数学模型的一般形式为
变量 m个
约束 ≤ ≥
= （方程） 系数矩阵
b c
变量 ≥0 ≤0
无非负约束 转置
c b
19
OR:SM
•
这样对于任意给定的一个线性规划问题，均可依据上述
对应关系直接写出其对偶问题模型，而无须先化成对称型。
• 例3 写出下列线性规划的对偶问题
max Z ( x) x1 2x2 x3
x1 x2 x3 2
7
OR:SM
• 首先，分析这两个模型之间的对应关系：
• （1）一个问题的目标函数为极大化，约束条件为“≤”类 型，另一个问题的目标为极小化，约束条件为“≥”类型；
• （2）一个问题的变量个数等于另一个问题的约束条件个数； • （3）一个问题的右端常数（约束系数）是另一个问题的目
标函数的系数（成本系数）； • （4）两个问题的系数矩阵互为转置。 • 我们把这种对应关系称为对偶关系。如果把（3-1）称为原
s.t.
2x1 x2 x1 x2 3
6x3 x3 0
6
x1, x3 0; x2 ?
• 写出其对偶问题
解：（1）首先把上述非对称型问题化为对称型问题。
①在第一个约束条件的两边同×（-1）
②把第三个约束方程分解成两个
x1-x2+3x3≤0
和
x1-x2+3x3≥0
再将后一个两边同×（-1）改写成
(3 3)
9
OR:SM
• 这种模型的特点是：
•
（1）目标函数是最大化类型(或是最小化类型)；
• （2）所有约束条件都是“≤”型（或都是“≥”型）；
• （3）所有决策变量都是非负的。
•
如果把（3-3）作为原始问题，根据原始与对偶问题
的对应关系可得（3-3）的对偶问题为
minW ( y) b1 y1 b2 y2 L bm ym
max Z (x) c1x1 c2 x2 L cn xn
Y1
a11x1 a12 x2 L a1n xn b1
Y2 …
s.t.
La21Lx1
L
a22 x2 L LLLL
a2n xn LL
b2
ym
am1x1 am2 x2 L amn xn bm
x1, x2 ,L , xn 0
y1 2 y2 y3 0
s.t.
0yy11
y2 y3 2 6 y2 3y3
5
y1, y2 0, y3 ?
17
OR:SM
•
综合上述两个例子，可以看出，线性规划与其对偶模型
的关系有了新的拓展：
• （1）一个问题的目标函数为极大化，约束条件为“≤”或
“=”类型，另一个问题的目标为极小化，约束条件为“≥”
a11 y1 a21 y2 L am1 ym c1
s.t. La12Ly1L
a22 y2 L LLLL
L
am2 ym L
c2
a1n y1 a2n y2 L amn ym cn
y1, y2 ,L , ym 0
(3 4)
10
OR:SM
• 用矩阵表示的原始问题（3-3）和对偶问题（3-4）为
买卖双方开始对资源的出让价格问题进行磋商，希望寻找一
个双方都认为比较满意的合理价格。
• 分析：设A、B、C三种材料的单价分别为y1、y2、y3.
•
对于卖方来说，生产单位甲产品所获收益为4万元，为保
证其总收入不少于405/2万元，则将生产单位甲产品所需资源
转让出去，该企业的收入不能少于4万元。故y1、y2、y3必须
minW ( y) 2 y1 6 y2 0 y3
y1 2 y2 y3 0
s.t.
0 y1 y1
y2 y3 2 6 y2 3y3
5
y1, y2 0; y3 ?
14
OR:SM
• 例2 将例1模型中的x2改为无非负约束变量，即模型为
max Z ( x) 2x2 5x3
x1 x3 2
80 90
x1, x2 0
(3 1)
运用单纯形法，可求得其最优解为：
x1 45 / 2, x2 45 / 2 Z (x) 405 / 2
5
OR:SM
• 新问题：现在从另一角度来讨论这个问题。
•
假设该企业经过市场预测，准备进行转产，且把现有三
种材料进行转让，也恰好有一个制造商急需这批材料。于是
满足约束条件： y1+2y2+y3≥4
•
同样，将生产单位乙产品所需的资源转让出去，其收入
不能少于生产单位乙产品的收益5万元，所以y1、y2、y3还必
须满足约束条件： y1+y2+3y3≥5
6
OR:SM
•
对于买方来说，他希望在满足上述约束条件下使总的
支出 • 达到最小。
W（y） =45y1+80y2+90y3
Y1
x1
6
Y2
x2 8
Y3
s.t.
x1
x2
7
Y4
3
x1
x2
15
Y5
x2 1
x1, x2 0
(3 7)
• 解：该问题仅有两个变量，但约束较多，其对偶问题为
minW ( y) 6 y1 8y2 7 y3 15y4 y5
y1 y3 3y4 4 s.t. y2 y3 y4 y5 3
根据对偶规划，很容易写出对偶问题的对偶模型。
2、对偶性定理 若原问题有最优解，那么对偶问题也有最优解，而且两者的 目标函数值相等。
22
OR:SM
• 3.1.5 对偶问题的最优解
• 重要推论： • 1.原始问题单纯形表中松驰变量的检验数恰好对应着对偶
问题的一个解。 • 2.原始问题单纯形表中,原始问题的松弛变量的检验数对应
-x1+x2-3x3≤0
12
OR:SM
• ③转换成对称型
max Z ( x) 0 x1 2 x2 5x3
Y1
x1 0 x2 x3 2
Y2 Y/3
s.t.
2 x1 x2 x1 x2 3
6 x3 x3 0
6
y//3
x1
x2
3x3
0
x1, x2 , x3 0
（2）写出相应的对偶问题（4个约束，分别对应4个对偶变量 y1、y2、y/3、y//3）
2
OR:SM
§3-1 线性规划的对偶理论
•
每一个线性规划问题都有一个与之相伴随的另一个问题。
这两个问题：一是，在数学模型上有着对应关系；二是，从
一个问题的最优解完全可以得出另一个问题最优解的全部信
息。
• 3.1.1 问题的提出
•
例1 引入一个资源价格问题。
3
OR:SM
类似于第2章例1的生产计划问题。某企业生产甲、乙两种 产品，需消耗A、B、C三种材料。据市场分析，单位甲、 乙产品的销售收益分别为4万元和5万元。单位甲、乙产品 对材料的消耗量及材料的供应量如表3.1所示。
2 y2 y2
y
y3/ y3//
/
3
y3/ /
2
0
s.t.0 y1 y2 y3/ y3// 2
y1 6 y2 3y3/ 3y3// 5
y1
,
y2 ,
y/ , 3
y3/ /
0
令y/3-y//3=y3,并将第二和第三个条件合并为方程，得
minW ( y) 2 y1 6 y2 0 y3
或“=”类型；
• （2）一个问题的变量个数等于另一个问题的约束条件个数；
• （3）一个问题的右端常数（约束系数）是另一个问题的目
标函数的系数（成本系数）；
• （4）两个问题的系数矩阵互为转置;
• （5）一个问题的第i个约束为“=”，则另一个问题的第i个
变量为“无非负约束变量”（自由变量）。反之，一个问题
s.t.
x1
x2
x3
1
2x1 x2 x3
2
x1 0; x2 , x3 ?
解：因目标函数为“max”类型，则约束条件应为“≤”和 “=”类型，故只需改变第三个约束条件的不等号方向， 即有：
2x1 x2 x3 2
20
OR:SM
原问题即为：
Y1 Y2 Y3
max Z (x) x1 2x2 x3