数学常数表

π值表的快速记忆方法全文共四篇示例，供读者参考第一篇示例：π是一个非常重要的数学常数，其值约等于3.14159。

在数学、物理、工程等领域中，π常常会出现在各种公式和计算中。

π的值是一个无限不循环小数，因此无法准确地用有限的小数表示。

为了方便计算和记忆π的值，人们制作了各种π值表。

今天我将向大家介绍一种关于π值表的快速记忆方法。

我们需要知道π的近似值是3.14159。

这个近似值可以帮助我们在计算中快速估算π的大小。

接下来，我们可以通过记忆π值表中的一些常见数值来帮助我们计算。

在π值表中，经常会出现一些常见的π值，例如π/4、π/3、π/2、2π/3、3π/4等。

这些值在各种公式和计算中经常会出现，因此我们可以通过记忆这些常见的π值来帮助我们进行快速计算。

我们还可以通过一些简单的规律来记忆π值表。

我们知道π是一个无限不循环小数，因此π的值是一个无限不循环的数字序列。

我们可以通过一些特殊的规律来记忆π的近似值。

我们还可以通过一些有趣的方法来帮助我们记忆π的近似值。

我们可以将π的值与一些具体的事物或图像联系起来，通过观察这些事物或图像，来帮助我们回忆π的值。

通过以上这些方法，我们可以在日常生活和工作中方便快速地记忆π值表，从而更好地应用π的概念和数值。

希望以上方法可以帮助大家更好地理解和应用π的概念，提高计算效率和准确性。

祝大家学习进步！第二篇示例：π值是代表圆周率的一个重要数值，它是一个无理数，约为3.14159。

在数学、物理等领域中都有广泛的应用，因此对π值的熟记是非常重要的。

但是π值是一个无限不循环小数，记忆起来很困难。

今天我们来分享一些关于π值表的快速记忆方法，希望可以帮助大家更轻松地记住这一重要数值。

我们可以利用一些记忆技巧来简化π值的记忆。

我们可以利用数字的规律进行记忆。

所谓数字的规律，就是数字之间有一定的联系和规律，我们可以利用这些规律来记忆数字。

π值的前几位小数是3.14159，我们可以将这些数字同音字或者谐音词联系起来，形成一个有意义的词语或短语。

科学常数e1. 引言科学常数e是数学中一个重要的常数，它是一个无理数，约等于2.71828。

e的定义方式有多种，但最常见的定义是通过自然对数的极限形式来定义。

e在数学、物理学和工程学等领域有着广泛的应用，被认为是自然界中的一种基本规律。

2. 历史e最早由瑞士数学家Leonhard Euler在18世纪提出，并以自然对数的极限形式来定义。

在此之前，e已经被一些数学家发现并研究，但Euler对e的研究使其成为一个重要的数学常数。

3. 定义e可以通过多种方式进行定义，其中最常见的是通过自然对数的极限形式：e = lim(n→∞) (1 + 1/n)^n这个定义表明，当n趋向于无穷大时，(1 + 1/n)^n的极限收敛到e。

4. 性质e有许多重要的数学性质，下面介绍其中几个：•e是一个无理数，无法表示为两个整数的比值。

•e是一个超越数，无法通过有限次四则运算和开方得到。

•e的小数部分是无限不循环的，它的十进制表示是无限不尽的。

•e的平方是一个无理数，即e^2是无法表示为两个整数的比值。

5. 应用e在数学、物理学和工程学等领域有着广泛的应用，下面介绍其中几个重要的应用：5.1 指数函数e^x是一个重要的指数函数，它在数学中有着广泛的应用。

指数函数在数学建模和解决微分方程等问题中起着重要的作用。

5.2 概率与统计e在概率与统计中有着重要的应用。

例如，在概率论中，e可以用来计算随机变量的期望值和方差。

在统计学中，e可以用来估计样本的标准差和置信区间。

5.3 复利计算e在金融学中有着重要的应用。

复利计算是指将利息再投资以获取更多利息的过程。

e可以用来计算复利的增长率，从而帮助人们做出更好的投资决策。

5.4 泰勒级数e在微积分中有着重要的应用。

泰勒级数是一种将函数表示为无穷级数的方法，e的出现使得许多函数可以用泰勒级数来表示，从而简化了函数的计算和分析。

6. 结论科学常数e是数学中一个重要的常数，它是一个无理数，约等于2.71828。

数学表白100个公式数学是一门奇妙的科学，她以精确、逻辑和严谨而著称，可以被视为宇宙的规律之一、而在这1200字中，我要向数学表白，让我们共同探索她的美丽世界，一起来看看100个重要的数学公式吧。

1.埃拉托斯特尼筛法：用于找出一定范围内的所有素数。

2.欧拉公式：e^(iπ)+1=0，融合了五个重要的数学常数。

3.二项式定理：展开(x+y)^n的公式。

4. 欧拉恒等式：e^(iθ) = cosθ + isinθ，链接了三角函数和指数函数。

5.费马定理：没有大于2的整数幂满足a^n+b^n=c^n的方程。

6. 黎曼猜想：Riemann Hypothesis，涉及到素数分布。

7.傅里叶级数：将任意周期函数表示为一系列三角函数的和。

8.泰勒级数：将函数表示为无穷级数的形式。

9. 黎曼积分：Riemann Integral，求解定积分的方法。

10.微积分基本定理：微分和积分是互为逆过程。

11.群论公理：群的定义和性质。

12.帕斯卡三角形：组合数的图形化表示。

13.莫比乌斯反演公式：利用莫比乌斯函数做函数变换。

14.卡诺图：寻找逻辑电路最简化的方法。

15.哈密顿四元数：扩展了复数的概念。

16.矩阵行列式：表示线性方程组的性质。

17.复变函数柯西-黎曼方程：复变函数的基本性质。

18.指数分布函数：用来描述独立随机事件发生的规律。

19.离散傅里叶变换：对离散信号进行频谱分析。

20.图论的欧拉公式：v-e+f=2，描述了平面图的一种关系。

21.莱布尼茨公式：对带参数的积分求导。

22.辗转相除法：求解最大公约数的方法。

23.卡尔曼滤波器：利用状态方程和观测方程进行估计和预测。

24.斯特林公式：近似计算阶乘的方法。

25.向量叉积公式：向量积的计算公式。

26.泊松分布：用来描述稀有事件发生的概率。

27.考雷-汉明距离：衡量两个等长字符串之间的差异。

28.费曼图：粒子物理学中的图形表示法。

29.默滨斯基三角形：组合数的一种图形化表示。

初一数学“什么叫常数”介绍---------------------------------------------------------------------- 初中数学常数是指一个数值不变的常量，与之相反的是变量。

跟大多数物理常数不一样的地方是，数学常数的定义是独立于所有物理测量的。

数学常数通常是实数或复数域的元素。

数学常数可以被称为是可定义的数字。

常数指的是规定的数量与数字，如圆的周长和直径的比T、铁的膨胀系数为0.000012等。

常数是具有一定含义的名称，用于代替数字或字符串，其值从不改变。

数学上常用大写的C来表示某一个常数。

一、常数的多重含义1.规定的数量与数字。

2.一定的重复规律。

3.一定之数或通常之数。

4.一定的次序。

5.数学名词。

固定不变的数值。

如圆的周长和直径的比值(T )约为3.14159、铁的膨胀系数为0.000012等。

常数是具有一定含义的名称，用于代替数字或字符串，其值从不改变。

一个数学常数是指一个数值不变的常量，与之相反的是变量。

跟大多数物理常数不一样的地方是，数学常数的定义是独立于所有物理测量的。

数学常数通常是实数或复数域的元素。

数学常数可以被称为是可定义的数字（通常都是可计算的）。

其它可选的表示方法可以在数学常数(以连分数表示排列)中找到。

常数又称定数，是指一个数值不变的常量，与之相反的是变量。

（常数多指大于零的数)6.物理名词。

在物理学上，很多经测量得出的数值都被称为常数。

例如万有引力系数和地表重力加速度等。

但有研究表明，部分这类常数并不是恒定不变的，因此就被称作“不定常数”和“不恒定的常数”。

二、初中常数的定义常数是除了字母以外的任何其他数，数学常数一般可以被称为可被定义的数字，用于代替数字或字符串，包括正负整数和正负小数、分数、0和无理数。

通常都是可计算的。

常数是具有一定含义的名称，值从不改变。

一个数学常数是指一个数值不变的常量，与之相反的是变量。

圆周率常数。

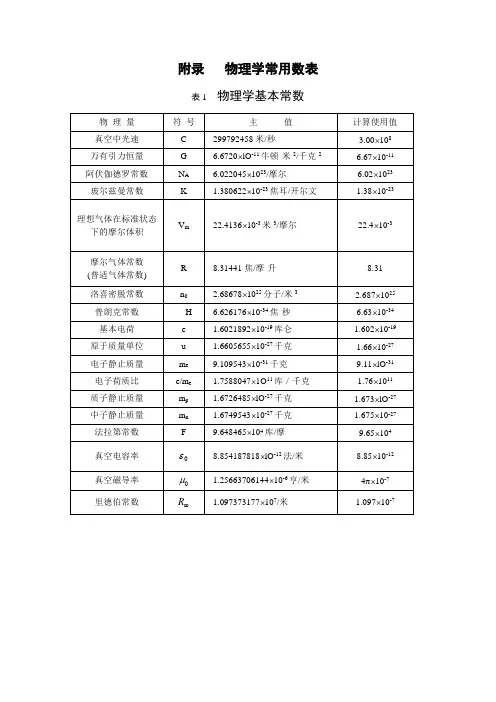
附录物理学常用数表表1 物理学基本常数
表2 我国某些城市的重力加速度（单位：米/秒2）
表3 一般固态物质的密度（克/厘米3）
表4 液体密度(克/厘米3)
表5 水的表面张力系数α随温度t的变化
表6 几种物质的绝对折射率和临界角
表7 常用光谱灯的可见谱线波长(nm)
表8 常用仪器量具的主要技术指标和极限误差
注：一般而言，有刻度的仪器、量具的最大允差大约对应于其最小分度值所代表的物理量；对于数学式仪表，测量值的误差往往在于所显示的能稳定不变的数字中最末一位的半个单位所代表的物理量。

应当说明，“最大允差”是指所制造的同型号同规格的所有仪器中有可能产生的最大误差，并不表明每一台仪器的每个测量值都有如此之大的误差，它既包括仪器在设计、加工、装配过程中乃至材料选择中的缺欠所造成的系统误差，也包括正常使用过程中测量环境和仪器性能随机涨落的影响。

表9 常用电气仪表面板上的标记符号。

起源e，作为数学常数，是自然对数函数的底数。

有时称它为欧拉数（Euler number），以瑞士数学家欧拉命名；也有个较鲜见的名字纳皮尔常数，以纪念苏格兰数学家约翰·纳皮尔(John Napier)引进对数。

它就像圆周率π和虚数单位i，e是数学中最重要的常数之一。

它的其中一个定义是，其数值约为（小数点后100位）：“e ≈ 2.71828 18284 59045 23536 02874 71352 66249 77572 47093 69995 95749 66967 62772 40766 30353 54759 45713 82178 52516 64274”。

第一次提到常数e，是约翰·纳皮尔(John Napier)于1618年出版的对数著作附录中的一张表。

但它没有记录这常数，只有由它为底计算出的一张自然对数列表，通常认为是由威廉·奥特雷德(William Oughtred)制作。

第一次把e看为常数的是雅各·伯努利(Jacob Bernoulli)。

已知的第一次用到常数e，是莱布尼茨于1690年和1691年给惠更斯的通信，以b表示。

1727年欧拉开始用e来表示这常数；而e第一次在出版物用到，是1736年欧拉的《力学》(Mechanica)。

虽然以后也有研究者用字母c表示，但e较常用，终于成为标准。

用e表示的确实原因不明，但可能因为e是“指数”(exponential)一字的首字母。

另一看法则称a，b，c和d有其他经常用途，而e是第一个可用字母。

不过，欧拉选这个字母的原因，不太可能是因为这是他自己名字Euler的首字母，因为他是个很谦虚的人，总是恰当地肯定他人的工作。

很多增长或衰减过程都可以用指数函数模拟。

指数函数的重要方面在于它是唯一的函数与其导数相等（乘以常数）。

e是无理数和超越数（见林德曼—魏尔施特拉斯定理(Lindemann-Weierstrass)）。

生活中的常数的概念生活中的常数，或称数学常数，是指一个数值不变的常量，例如圆的周长和直径的比值π，铁的膨胀系数等。

这些常数在数学和物理学中经常被使用，用于描述和预测各种现象。

此外，常数还可以指代一些具有特定含义的名称，这些名称用于代替数字或字符串，其值在定义后不会改变。

在数学中，常数通常用来表示某种固定的量或属性，如速度、加速度、电阻等。

在日常生活和科学研究中，常数也扮演着重要的角色。

例如，在物理学中，万有引力系数和地表重力加速度等常数被用来描述和计算各种与力相关的现象。

在化学中，各种化学反应的平衡常数被用来描述反应的条件和速率。

总之，生活中的常数是指那些具有固定数值或含义的量或属性，它们在数学、物理学、化学等领域中被广泛应用，用于描述和预测各种现象。

具体的生活中的常数例子：1.圆周率 (π)：这是一个无理数，约等于3.14159。

它表示圆的周长与直径的比值，无论圆的大小如何，这个比值始终保持不变。

在几何学、物理学以及日常生活中，π都有广泛的应用，例如计算圆的面积、球的体积、圆柱的侧面积等。

2.自然对数的底数 (e)：这也是一个无理数，约等于2.71828。

它在自然对数、指数函数以及许多其他数学和物理公式中都有出现。

例如，在复利计算、人口增长模型、放射性衰变等场景中，e都扮演着重要的角色。

3.光速 (c)：在真空中，光的传播速度约为299,792,458米/秒。

这是物理学中的一个基本常数，它在相对论、电磁学以及许多其他物理领域中都有应用。

4.万有引力常数 (G)：这个常数描述了物体之间的引力作用，其值约为6.67430 × 10⁻¹¹ N·(m/kg)²。

在牛顿的万有引力定律中，G是一个关键参数，用于计算两个物体之间的引力。

5.黄金比例 (φ)：这是一个无理数，约等于1.61803。

它在艺术、建筑、自然界以及许多其他领域中都有出现。

例如，许多植物的叶子和花瓣的排列都遵循黄金比例，而一些著名的艺术品如达芬奇的《蒙娜丽莎》和米开朗基罗的《大卫像》也被认为具有黄金比例的美。

常数的符号
常数的符号通常可以用大写的英文字母"C"来表示。

在数学中，常数是指规定的数量与数字，如圆的周长和直径的比π，或是数学公式中的具体数值。

常数的符号可以用于代替数字或字符串，其值从不改变。

此外，不同的常数有不同的常用符号，举例如下：
* π（圆周率）
* e（自然对数的底数）
* i（虚数单位）
* c（光速）
* G（引力常数）
* h（普朗克常数）
* k（玻尔兹曼常数）
* R（气体常数）
* α（精细结构常数）
* Avogadro常数 (NA)（阿伏伽德罗常数）
以上信息仅供参考，如有需要，建议查阅数学专业书籍或者咨询数学专业人士。

筑龙网WW W.ZH UL ON G.CO M测量常用数据数学常数圆周率：π=3.141592654 自然对数底 e=2.718281828 对数模 loge=0.4342944819 弧度化算 1弧度=57.295777951 度 =3437.746771 分 =206264.8062 秒大气折射率 n=1+n ′×10-8Hkm 0.0 1.0 2.0 3.0 4.0 5.0 6.0 7.0 8.0 9.0n ′ 27685 25131 22758 20548 18509 16634 14916 13334 11884 10554地球其他常数地日距 =1.946×108 km 地月距 =3.844×105 km 地球密度 =5.517g/cm2地球总重量 =5.976×1021 公吨 地球表面积 =5.11×108 km2中国各旧有高程系统间的概略关系 平均海水面较差系统名称 坎门 大沽 吴凇 罗星塔筑龙网WW W.ZH UL ON G.CO M较差 +0.228 -1.296 -1.805 -2.179两个基准高程系统的换算 H85=H56-0.029m 根据网友的需要不断添加水准原点(高程基准)1956年黄海高程系(1950—1956黄海平均海水面) 水准原点（青岛原点）高程为72.289m1985年国家高程基准(1952—1979黄海平均海水面) 水准原点（青岛原点）高程为72.260m我国地形图基本比例尺1:5千 1:1万 1:2.5万 1:5万 1:10万 1:25万 1:50万 1:100万。

e的由来e，作为数学常数，是自然对数函数的底数。

有时称它为欧拉数（Euler number），以瑞士数学家欧拉命名；也有个较鲜见的名字纳皮尔常数，以纪念苏格兰数学家约翰•纳皮尔引进对数。

它就像圆周率π和虚数单位i，e是数学中最重要的常数之一。

它的数值约是（小数点后100位）：e ≈ 2.71828 18284 59045 23536 02874 71352 66249 77572 47093 69995 95749 66967 62772 40766 30353 54759 45713 82178 52516 64274 第一次提到常数e，是约翰•纳皮尔于1618年出版的对数著作附录中的一张表。

但它没有记录这常数，只有由它为底计算出的一张自然对数列表，通常认为是由威廉•奥特雷德(William Oughtred)制作。

第一次把e看为常数的是雅各•伯努利(Jacob Bernoulli).已知的第一次用到常数e，是莱布尼茨于1690年和1691年给惠更斯的通信，以b表示。

1727年欧拉开始用e来表示这常数；而e第一次在出版物用到，是1736年欧拉的《力学》(Mechanica)。

虽然以后也有研究者用字母c表示，但e较常用，终于成为标准。

用e表示的确实原因不明，但可能因为e是“指数”(exponential)一字的首字母。

另一看法则称a，b，c和d有其他经常用途，而e是第一个可用字母。

不过，欧拉选这个字母的原因，不太可能是因为这是他自己名字Euler的首字母，因为他是个很谦虚的人，总是恰当地肯定他人的工作。

很多增长或衰减过程都可以用指数函数模拟。

指数函数的重要方面在于它是唯一的函数与其导数相等（乘以常数）。

e是无理数和超越数（见林德曼—魏尔施特拉斯定理(Lindemann-Weierstrass)）。

这是第一个获证为超越数，而非故意构造的（比较刘维尔数）；由夏尔•埃尔米特(Charles Hermite)于1873年证明。

大学数学符号表数学作为一门精确的科学学科，其符号体系在代数、几何、统计学等各个领域都有广泛应用。

为了更好地理解和应用数学，熟悉数学符号是必不可少的。

本文将为大家介绍一些大学数学中常见的符号及其含义。

1. 希腊字母希腊字母在数学中被广泛使用，它们通常代表特定的数学对象或常数。

- α（Alpha）: 代表某个角度的度数或系数。

- β（Beta）: 通常用于表示常数或系数。

- γ（Gamma）: 代表某个角度的度数或系数。

- δ（Delta）: 常用于表示增量、差量或变化率。

- ε（Epsilon）: 一般表示接近零或无穷小量。

- ζ（Zeta）: 代表某个特殊函数值，即黎曼ζ函数。

- η（Eta）: 一般用于表示某个集合中的元素。

- θ（Theta）: 通常用于表示角度。

- ι（Iota）: 主要用于表示单位根或虚数单位。

- κ（Kappa）: 代表比率或常数。

- λ（Lambda）: 通常用于表示特定的特征值或波长。

- μ（Mu）: 一般用于表示均值。

- ν（Nu）: 代表频率或流体的运动性质。

- ξ（Xi）: 一般用于表示某个集合中的元素。

- ο（Omicron）: 很少被使用。

- π（Pi）: 代表圆周率，即3.14159。

- ρ（Rho）: 通常用于表示密度。

- σ（Sigma）: 代表总和或标准差。

- τ（Tau）: 通常用于表示时间常数或周期。

- υ（Upsilon）: 很少被使用。

- φ（Phi）: 一般表示某个函数或系数。

- χ（Chi）: 很少被使用。

- ψ（Psi）: 一般用于表示某个特殊函数值，即角谱函数。

- ω（Omega）: 代表角速度或无穷远。

2. 常见函数符号函数符号在数学中广泛应用，表示不同的数学运算和关系。

- f(x): 代表函数f中自变量为x。

- g(x): 代表函数g中自变量为x。

- h(x): 代表函数h中自变量为x。

- sin(x): 代表正弦函数，其中x为角度。

二项式展开式中的常数项
首先，让我们来了解一下什么是二项式展开式。

二项式展开式是数学中最常用的扩展方法。

它表示将二项式 (a + b)n分成有n项的和，每一项可以用an-k bk记，其中，a、b 为两个不同的变量，n 为一个正整数，k 为一个介于 0 n 之间的整数。

接下来，让我们来讨论一下二项式展开式中的常数项。

常数项是指每个二项式展开式中只有一个项，也就是 k只有 0项，它只有 a n 方。

如果 a 为 1，则该项为 1；如果 a 为 -1，则该项为 -1。

比如(1 + x)5、(2 + y)8、(-5 + z)7 中的常数项都是 1，而 (3 + n)4、(-4 + m)4、(-3 + n)6 中的常数项分别为 81、256 -729。

二项式展开式中的常数项对于我们来说十分重要，因为它决定着最终的结果。

有的时候，常数项的取值范围会影响我们对结果的判断，比如当展开式的常数项为负数时，结果一般会比原来想象的更小。

另外，常数项还可以用来判断展开式的幅度，比如有的时候常数项比较大，则表明展开式的幅度较大，如果常数项比较小，则表明展开式的规模较小。

总而言之，二项式展开式中的常数项十分重要，因为它可以反映出展开式的形式，也可以影响结果的大小。

因此，我们要时刻关注二项式展开式中的常数项，努力掌握它们的取值范围，以便更有效地使用二项式展开式来解决各种数学问题。

- 1 -。

常数0、1、、e、i五兄妹汉中市铺镇中学杨瑞杰0、1、、e、i是数学中很重要的五个常数，是在学习数学过程中逐渐认识理解掌握的五个数，0、1、、e、i这五个数与人们的生活息息相关，也是人们解决实际问题经常用到的数。

0、1、、e、i 这五个“兄妹”被大数学家欧拉（最丰产的数学家）统一在著名的、简洁的、优美的公式eπi+1=0中。

为了纪念数学家欧拉，公式eπi+1=0称为欧拉公式。

“0”是阿拉伯数字之一。

国际通用的数字，就是0，1，2，3，4，5，6，7，8，9这十个阿拉伯数字。

古代印度人发明了包括“零”在内的十个数字符号，还发明了现在一般通用的定位计数的十进位法。

由于定位计数，同一个数字符号因其所在位置不同，就可以表示不同数值。

如果某一位没有数字，则在该位上写上“0”。

“0”的应用，使十进位法臻于完善，意义重大。

十个数字符号后来由阿拉伯人传人欧洲，被欧洲人误称为阿拉伯数字。

由于采用计数的十进位法，加上阿拉伯数字本身笔划简单，写起来方便，看起来清楚，特别是用来笔算时，演算很便利。

因此随着历史的发展，阿拉伯数字逐渐在各国流行起来，成为世界各国通用的数字。

虽然阿拉伯数字看起来很简单，但它是我们数学必用、而且全球共用，生活不可少的发明。

在公元7世纪，印度数学家婆罗摩笈多（Brahmagupta）将0作为一个“数字”对待，并且建立了一套使用规则。

这些规则包括“正数和零相加的结果仍为正数”及“零和零相加仍为零”。

0有什么作用，没有0将万事难行，科学的进步依靠它。

我们常谈论0度经线，温度标尺上的00C，以及类似的0能量、0重力等。

这种思想同样进入了非科学的语言里，例如零时（发动进攻等的时刻）、零容忍（指对轻微过失都不予放过的严厉执法政策）。

没有0就不成数学。

它处在数学概念的最核心位置，使得数字系统、代数、几何得以成立。

在数字序列中，0将正数和负数区分开来，因此占据了一个享有特权的位置。

在十进制系统中，0作为占位符，使得我们既可以使用很大的数，也可以使用很精微的数字。