数据特征的测度
- 格式:doc
- 大小:127.50 KB
- 文档页数:6
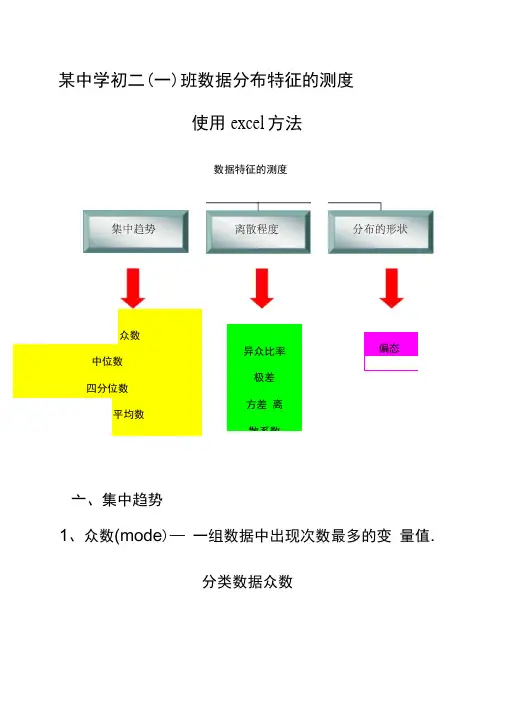
某中学初二(一)班数据分布特征的测度使用excel 方法数据特征的测度众数 中位数 四分位数平均数亠、集中趋势1、众数(mode )— 一组数据中出现次数最多的变 量值.分类数据众数偏态 峰态异众比率 极差 方差 离散系数制作:用frequency 函数求出语文成绩的频数一求 出各个分数段的比例一各个分数段的百分比.原始数据:原始数据一众数・xls2、中位数(median )-排序后处于中间位置上的值解:这里的变量为“成绩 分数段”,这是个分类变 量,不同的分数段就是变 量值。
所调查的初二一班 60人 中,60-69这个分数段的人 数最多,为23人,占全班 人数的38.33%,因此众数 为“ 60-69这一分数段”。
即:M=60-69这一分数段制作:对语文成绩进行降序排列一根据计算公式求得中位数/插入median函数求得中位数要求得这60名学生语文成绩的中位数有2种方法:方法一:1、首先对学生的语文成绩进行降序排列。
2、由于学生人数为偶数,所以位置计算公式二错误!位置=错误!—错误!= 30。
5语文成绩中位数=错误!= 68方法二:插入median函数一求得语文成绩中位数。
原始数据-中位数:原始数据一中位数。
XlS3、四分位数(quartile)—排序后处于25%和75%位置上的值.要求得这60名学生语文成绩的中位数有2种方法: 方法一:1、首先对学生的语文成绩进行升序排列。
2、由于学生人数为偶数,所以位置计算公式为:Q 位置二错误!=错误!= 15.25Q位置二错误!=错误!= 45。
75Q= 61+0.75 X( 62-61 ) =61。
75Q= 78+0。
25 X( 78—78) =78方法二:使用函数QUARTILE求出语文成绩的四分位数xls 原始数据一四分位数:原始数据-四分位数。
4、平均数(mean)加权平均数一初二(一)班语文总评成绩总评成绩=错误!原始数据一平均数:原始数据一平均数。




中级经济师《经济基础知识》第二十四章课后练习【单选题】下列指标中,应采用算术平均方法计算平均数的是()。
A. 企业年销售收入B. 男女性别比C. 国内生产总值环比发展速度D. 人口增长率【答案】A【解析】考核集中趋势的测度。
本题用排除法选择,几何平均数的主要用途:(1)对比率、指数等进行平均(2)计算平均发展速度。
【单选题】集中趋势的测试,主要包括()。
A. 方差和标准差B. 众数和离散系数C. 标准分数D. 中位数和众数【答案】D【解析】集中趋势的测试,主要包括:均值、中位数、众数和均值、中位数和众数的比较及适用范围。
【单选题】()的测度值是对数据一般水平的一个概括性变量,它对一组数据的代表程度,取决于该组数据的()。
A. 集中趋势;离散程度B. 离散程度;集中程度C. 极差;组距D. 方差;算术平均数【答案】A【解析】集中趋势的测度值是对数据一般水平的一个概括性变量,它对一组数据的代表程度,取决于该数据的离散程度。
【单选题】一家连锁酒店8个分店某月的营业额(单位:万元)为:60、60、70、80、80、70、70、65,那么这8个分店月营业额的中位数为()。
A. 60B. 65C. 70D. 80【答案】C【解析】中位数首先要将数据进行排列,从小到大排列的结构时60,60,65,70,70,70,80,80,则中位数第4个数和第5个数的均值,即(70+70)/2=70【单选题】2010年某省8个地市的财政支出(单位:万元)分别为:59000,50002,65602,66450,78000,78000,78000,132100这组数据的中位数是()万元。
A. 78000B. 72225C. 66450D. 75894【答案】B【解析】对数据进行排序后是:50002,59000,65602,66450,78000,78000,78000,132100所以中位数的位置是第4个和第5个数据的平均数。


2021年中级统计师答案1.下列测度集中趋势的指标中适用于顺序数据的是()。
[单选题] *A.均值B.中位数(正确答案)C.标准差D.方差答案解析:标准差和方差为离散程度的测度指标,可排除C、D;集中趋势的指标有均值、中位数、众数;其中均值主要适用于数值型数据,但不适用于分类和顺序数据;中位数主要适用于数值型数据和顺序数据,但不适用于分类数据;众数适用于顺序数据和分类数据,但不适用于描述定量数据的集中位置,故选择B选项。
2.下列数据特征的测度值中,不受极端值影响的是()。
[单选题] *A.均值B.中位数(正确答案)C.标准差D.方差答案解析:中位数的优点就是不受极端值影响,抗干扰性强,尤其适用收入这类偏斜分布的数值型数据。
3.某城市2014年4月空气质量检测结果中,随机抽取6天的质量指数进行分析。
样本数据分别是:30、40、50、60、80和100,这组数据的平均数是()。
[单选题] *A.50C.60(正确答案)D.70答案解析:2014年考题。
(30+40+50+60+80+100)÷6=60。
4.下列数据特征测度中,是用于反映偏斜分布数值型数据集中趋势的是()。
[单选题] *A.离散系数B.方差C.标准差D.中位数(正确答案)答案解析:2013、2014年考题,中位数不受极端值影响,适用偏斜分布的数值型数据。
5.下面一组数据为9个家庭的人均月收入数据(单位:元):900;880;850;960;1080;1550;1500;1650;2000;则中位数为()。
[单选题] *A.850B.1080(正确答案)C.1500D.2000答案解析:先排序,题目中数据从小到大排850;880;900;960;1080;1500;1550;1650;2000,n为奇数,(n+1)/2为中位数的位置为5,该位置所对应的数值就是中位数数值,中位数的数值为1080。
6.某小学六年级8个班的学生人数由少到多依次为34人、34人、34人、34人、36人、36人、37人、37人,其中位数为()。


第四章数据分布特征的测度一、选择题1.一组数据中出现频数最多的变量值称为()。
A.众数B.中位数C.四分位数D.均值2.下列关于众数的叙述,不正确的是()。
A.一组数据可能存在多个众数B.众数主要适用于分类数据C.一组数据的众数是唯一的D.众数不受极端值的影响3.一组数据排序后处于中间位置上的变量值称为()。
A.众数B.中位数C.四分位数D.均值4.一组数据排序后处于25%和75%位置上的值称为()。
A.众数 B.中位数C.四分位数D.均值5.非众数组的频数占总额数的比率称为()。
A.异众比率B.离散系数C.平均差D.标准差6.如果一个数据的标准分数是-2,表明该数据()。
A.比平均数高出2个标准差B.比平均数低2个标准差C.等于2倍的平均数D.等于2倍的标准差7.比较两组数据的离散程度最适合的统计量是()。
A.极差B.平均差C.标准差D.离散系数8.偏度系数测度了数据分布的非对称性程度。
如果一组数据的分布是对称的,则偏度系数()。
A.等于0 B.等于1 C.大于0 D.大于1 9.某专家小组成员的年龄分别为29,45,35,43,45,58,他们的年龄中位数为()。
A.45 B.40 C.44 D.3910.某居民小区准备建一个娱乐活动场所,为此,随机抽取了80户居民进行调查,其中表示赞成的有59户,表示中立的有12户,表示反对的有9户。
该组数据的中位数是()。
A.赞成B.59 C.中立D.1211.对于右偏分布,均值、中位数和众数之间的关系是()。
A .均值>中位数>众数B .中位数>均值>众数C .众数>中位数>均值D .众数>均值>中位数12.某班学生的大学英语平均成绩是70分,标准差是10分。
如果已知该班学生的考试分数为对称分布,可以判断成绩在60分~80分之间的学生大约占( )。
A .95%B .89%C .68%D .99%13.当一组数据中有一项为零时,不能计算( )。
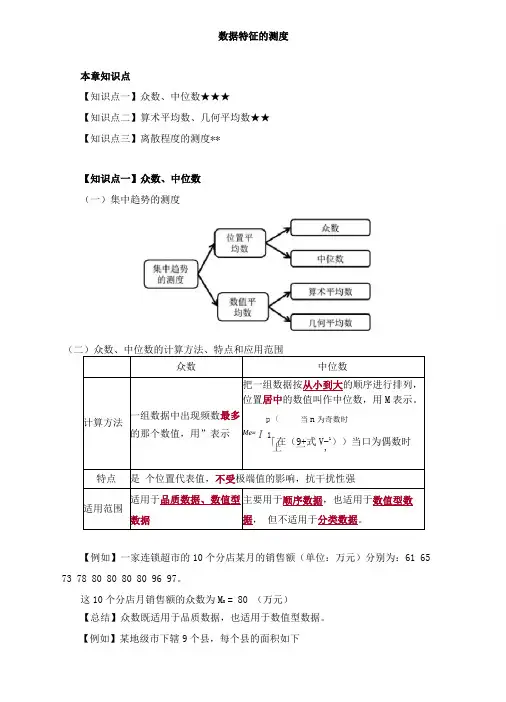
数据特征的测度本章知识点【知识点一】众数、中位数★★★【知识点二】算术平均数、几何平均数★★【知识点三】离散程度的测度**【知识点一】众数、中位数(一)集中趋势的测度【例如】一家连锁超市的10个分店某月的销售额(单位:万元)分别为:61 65 73 78 80 80 80 80 96 97。
这10个分店月销售额的众数为M0 = 80 (万元)【总结】众数既适用于品质数据,也适用于数值型数据。
【例如】某地级市下辖9个县,每个县的面积如下(单位:平方公里),计算该市下辖县面积的中位数:1455 2019 912 1016 1352 1031 2128 1075 2000首先,将上面的数据排序:912 1016 1031 1075 1352 1455 2000 2019 2128中位数位置=(9 + 1)+2 = 5,中位数为1352,即Me = 1352 (平方公里)【总结】中位数主要适用于顺序数据,也适用于数值型数据。
【例题•单选题】(2018年)2016年,某市下辖6个县的棉花种植面积按规模由小到大依次为800亩、900亩、1100亩、1400亩、1500亩、3000亩。
这组数据的中位数为()亩。
A.1100B.1250C.1400D.1450『正确答案』B『答案解析』本题考查中位数的应用。
中位数=(1100+1400)+2 = 1250。
【知识点二】算术平均数、几何平均数(一)算数平均数的特点、适用范围(二)两种算数平均数的比较【例如】某售货小组有5名营业员,元旦一天的销售额分别为520元、600元、480 元、750元和500元,求该日每名营业员的平均销售额。
于_旦+筋+…L=-------------- = ------ 520+600+480 + 750 + 500 、JC = ---------- ---------- =570(>L)【例如】某市商业企业协会根据100个会员样本,整理出一年销售额分布资料:销售额分布资料计算年平均销售额。
第四章数据分布特征的测度学习目的和要求:通过本章的学习,掌握数据分布特征的各种描述方法;掌握不同测度方法的特点、应用条件及应用场合;能利用所学的方法对统计数据作各种统计描述。
难点释疑:(一)算术平均数通常用来反映总体分布的集中趋势,调和平均数往往只作为算术平均数的变形来使用,即在已知标志总量而未知总体单位总量的情况下计算调和平均数;而几何平均数较适用于计算平均比率和平均速度。
(二)调和平均数虽然是根据标志值的倒数计算的,但其结果不等于算术平均数的倒数。
在计算和应用平均指标时,除了考虑数理方面的要求外,更重要的是要考虑其现实的经济意义。
(三)平均数的性质是简捷计算法的基础,也是计算标志变异指标的基础。
掌握中位数和众数与算术平均数的关系的目的是能够根据其中的两个平均数大体计算出第三个平均数,并判断总体的分布状态。
(四)全距、四分位差、平均差、标准差在反映标志变异程度方面各有优缺点。
全距是描述数据离散程度的最简单测度值,它计算简单,易于理解,但不能全面反映总体各单位标志值的差异程度。
标准差与平均差的意义基本相同,但在数学性质上比平均差要优越,所以,在反映标志变动度大小时,一般都采用标准差。
标准差是实际中应用最广泛的离散程度测度值。
(五)标准差系数的应用。
为了对比和分析不同平均水平总体的标志差异程度,就需要使用标准差系数。
它是标志变异的相对指标。
它既消除了变量数列变量值差异程度的影响,也消除了变量数列水平高低的影响。
练习题:(一)单项选择题(在下列备选答案中,只有一个是正确的,请将其顺序号填入括号内)1.平均指标反映了()。
①总体变量值分布的集中趋势②总体分布的离散特征③总体单位的集中趋势④总体变动趋势2.加权算术平均数的大小( )。
①受各组标志值的影响最大 ②受各组次数的影响最大③受各组权数系数的影响最大 ④受各组标志值和各组次数的共同影响3.在变量数列中,如果变量值较小的一组权数较大,则计算出来的算术平均数( )。
第四章数据分布特征的测度【教学要求】了解绝对数和相对数的概念及作用,掌握绝对数的种类、相对数的种类及应用;掌握集中趋势的测度方法,掌握算术平均数、调和平均数、几何平均数、众数、中位数的计算方法及应用;掌握离散程度的测度方法,理解全距、四分位差、异众比率、平均差的概念及计算方法,掌握标准差、离散系数的计算方法及应用;了解偏态与峰度的测度方法。
【知识点】绝对数、相对数、术平均数、调和平均数、几何平均数、众数、中位数、全距、四分位差、异众比率、平均差、标准差、离散系数【本章重点】相对数的种类及应用;算术平均数、调和平均数、几何平均数、众数、中位数的计算方法及应用;理解全距、四分位差、异众比率、平均差的概念及计算方法,掌握标准差、离散系数的计算方法及应用。
【本章难点】算术平均数、调和平均数、几何平均数、众数、中位数的计算方法及应用;理解全距、四分位差、异众比率、平均差的概念及计算方法,掌握标准差、离散系数的计算方法及应用。
【教学内容】第一节绝对数和相对数统计指标就其具体内容来讲非常多,可谓成千上万,但从其基本形式看,则不外乎总量指标、相对指标和平均指标三种类型,统称统计综合指标。
一、绝对数(一)绝对数的概念和种类1、绝对数的作用主要表现在:(1)绝对数可以反映一个国家、地区、部门或单位的基本情况(2)绝对数是制定政策、编制计划以及进行科学管理的重要依据(3)绝对数是计算相对数和平均数的基础相对数和平均数是由两个有联系的总量指标对比计算出来的统计综合指标,无论是相对指标还是平均指标,都是总量指标的派生指标,没有总量指标就不会有相对指标和平均指标。
例如,职工劳动生产率、职工平均工资、宏观经济增长速度、国民经济发展的重要比例关系、农作物单位面积产量等都是在总量指标的基础上计算出来的。
(二)绝对数的种类1、按反映总体内容不同分为总体单位总量和总体标志总量。
例、某业企业职工人数1,000人,工资总额1980,000元。
集中趋势和离散程度是数据分布的两个重要特征,但要全面了解数据分布的特点,还需要掌握数据分布的形状是否对称、偏斜的程度以及扁平程度等。
反映这些分布特征的测度值有两个:(1)偏态;(2)峰度。
二、分布的偏态
(一)偏态的含义
偏态(Skewness)是对分布偏斜方向和程度的测度。
在客观实际生活中,一些现象变量的次数分配往往是非对称型的,如收入分配、市场占有份额、资源配置等等,这些变量经分组后,总体各单位在不同的分组变量值下分布并不均匀对称,而呈现出偏斜的分布状况,统计上将其称为偏态分布。
(二)偏态的测度
利用众数、中位数和平均数之间的关系就可以判断分布是对称、左偏还是右偏。
显然,判断偏态的方向并不困难,但要测度偏斜的程度则需要计算偏态系数。
统计分析中测定偏态系数的方法很多,一般采用动差概念计算。
由公式可知:当算术平均数大于众数时,偏态系数为正值,属于正偏(右偏);当算术平均数小于众数时,偏态系数为负值,属于负偏(左偏)
(三)采用矩的概念测定分布偏态
偏态系数的计算公式为三阶中心矩与标准差的三次方之比:
()3
13133
σσα⋅-==∑∑==n i i i n i i f f X X v 当高于平均数的离差之和与低于平均数的离差之和相等时,全部离差之和
峰度的测度0344
=-σ
v 在正态分布情况下:
因此有:
0344>-σ
v v 高峰。
数据特征的测度统计数据经过整理和显示后,我们对数据分布的类型和特点就有了一个大致的了解,但这种了解只是表面上的,还缺少代表性的数量特征值准确地描述出统计数据的分布。
为进一步掌握数据分布的特征和规律,进行更深入的分析,还需要找到反映数据分布特征的各个代表值。
对统计数据分布的特征,我们可以从三个方面进行测度和描述:一是分布的集中趋势,反映各数据向其中心值靠拢或聚集的程度;二是分布的离散程度,反映各数据远离其中心值的趋势;三是分布的偏态和峰度,反映数据分布的形状。
这三个方面分别反映了数据分布特征的不同侧面,这里我们主要讨论集中趋势和离散程度的测度方法。
(一)集中趋势的测度集中趋势是指一组数据向某一中心值靠拢的倾向,测度集中趋势也就是寻找数据一般水平的代表值或中心值。
集中趋势的测度值主要有众数、中位数、均值、几何平均数等几种。
1.众数众数是一组数据中出现次数最多的变量值,用0M 表示。
例如,下面是抽样调查的10个家庭住房面积(单位:平方米)的数据:55 75 75 90 90 90 90 105 120 150这10个家庭住房面积的众数为90。
即0M =90(平方米) 众数是一个位置代表值,它的特点是不受数据中极端值的影响。
2.中位数中位数是一组数据按一定顺序排序后,处于中间位置上的数值,用e M 表示。
显然,中位数将全部数据等分成两部分,每部分包含50%的数据,一部分数据比中位数大,另一部分则比中位数小。
根据未分组数据计算中位数时,要先对数据进行排序,然后确定中位数的位置,其公式为:21+n 中位数位置=式中的n 为数据的个数,最后确定中位数的具体数值。
设一组数据为1x ,2x ,…,n x ,按从小到大排序后为)1(x ,)2(x ,…,)(n x ,则中位数可表示为:⎪⎪⎩⎪⎪⎨⎧⎪⎪⎭⎫⎝⎛+=++为偶数时当为奇数时当n x x n x M n n n e 122)21(21 例如,在某城市中随机抽取9个家庭,调查得到每个家庭的人均月收入数据如下(单位:元):750 780 850 960 1080 1250 1500 1650 2000中位数位置=(9+1)÷2=5,中位数为1080,即e M =1080(元)。
假定我们抽取了10个家庭,每个家庭的人均月收入数据为: 660 750 780 850 960 1080 1250 1500 1650 2000 这时,中位数位置=(10+1)÷2=5.5,中位数为1020,即:102021080960=+=e M (元)中位数是一个位置代表值,其特点是不受极端值的影响,在研究收入分配时很有用。
3.均值均值也称为算术平均数,它是全部数据的算术平均。
均值在统计学中具有重要的地位,是集中趋势的最主要测度值,根据所掌握数据的不同,均值有不同的计算形式和计算公式。
(1)简单均值。
根据未经分组整理的原始数据计算均值。
设一组数据为1x ,2x ,…,n x ,则均值x (读作x-bar )的计算公式为:nx nx x x x ni in∑==+++=121例如,根据下面的例子,计算10个家庭的平均住房面积。
55 75 75 90 90 90 90 105 120 15094101501207555=++++=x (平方米)(2)加权均值。
根据分组整理的数据计算均值。
设原始数据被分成k 组,各组的组中值为1x ,2x ,…,k x ,各组变量值出现的频数分别为1f ,2f ,…,K f ,则均值的计算公式可以写为:∑∑===++++++=ki iki ii kk k f f x f f f f x f x f x x 11212211例如,假定我们在某城市中随机抽取50个家庭,调查住房面积,经分组后结果如表。
计算50个家庭的平均住房面积。
计算过程见表。
4-7 某城市50个家庭住房面积均值计算表代入上面的公式得:8.9850494011===∑∑==ki iki ii f f x x (平方米) 从加权均值可以看出,其数值的大小不仅受各组变量值(i x )大小的影响,而且受各组变量值出现的频数即权数(i f )大小的影响。
如果某一组的权数较大,说明该组的数据较多,那么该组数据的大小对均值的影响就越大,反之则越小。
实际上,我们将加权均值变形为下面的形式,就能更清楚地看出这一点。
∑∑∑∑====⋅==ki ki iii ki iki ii f f x f f x x 1111由上式可以清楚地看出,加权均值受各组变量(i x )值大小和各组权数∑=ki i if f 1大小的影响。
当我们掌握的不是各组变量值出现的频数,而是频率时,也可直接根据上面的公式计算均值。
均值在统计学中具有重要的地位,它是进行统计分析和统计推断的基础。
从统计思想上看,均值是一组数据的重心所在,是数据误差相互抵消后的必然性结果。
比如我们对同一事物进行多次测量,若所得结果不一致,可能是由于测量误差所致,也可能是其他因素的偶然影响,利用均值作为其代表值,则可以使误差相互抵消,反映出事物必然性的数量特征。
均值的缺点是容易受极端值的影响。
4.几何平均数几何平均数是n 个变量值乘积的n 次方根,计算公式为:nni inn x x x x G ∏==⨯⨯⨯=121式中:G 表示几何平均数,∏为连乘符号。
几何平均数是适用于特殊数据的一种平均数,它主要用于计算比率或速度的平均。
当我们所掌握的变量值本身是比率的形式,而且各比率的乘积等于总的比率,这时就应采用几何平均法计算平均比率。
在实际应用中,几何平均数主要用于计算社会经济现象的平均发展速度。
例如,一位投资者持有一种股票,在1996、1997、1998和1999年收益率分别为4.5%、2.0%、3.5%、5.4%。
计算该投资者在这四年内的平均收益率。
解:根据几何平均数的计算公式得:n n x x x G ⨯⨯⨯= 214%4.105%5.103%0.102%5.104⨯⨯⨯==103.84%即该投资者的年平均收益率为103.84%-100%=3.84%。
(二)离散程度的测度集中趋势只是数据分布的一个特征,它所反映的是各变量值向其中心值聚集的程度。
而各变量值之间的差异状况如何呢?这就需要考查数据的分散程度。
数据的分散程度是数据分布的另一个重要特征,它所反映的是各变量值远离其中心值的程度。
我们知道,集中趋势的各测度值是对数据一般水平的一个概括性度量,它对一组数据的代表程度,取决于该组数据的离散水平。
数据的离散程度越大,集中趋势的测度值对该组数据的代表性就越差,离散程度越小,其代表性就越好。
数据离散程度测度值有很多,这里我们主要介绍极差、标准差和离散系数等。
1.极差极差也称全距,它是一组数据的最大值与最小值之差。
即: 极差=最大值-最小值 例如,根据上面10个家庭月人均收入的数据,计算的极差为:极差=139-107=32(件)。
极差是描述数据离散程度的最简单测度值,计算简单,易于理解,但它容易受极端值的影响。
由于极差只是利用了一组数据两端的信息,不能反映出中间数据的分散状况,因而不能准确描述出数据的分散程度。
2.标准差标准差是各变量值与其均值离差平方和的平均数的平方根,它是数测量数据离散程度的最主要方法,也是实际中应用最广泛的离散程度测度值。
设标准差为σ,对于未经整理的原始数据,标准差的计算公式为:nx x ni i ∑=-=12)(σ对于组距分组数据,标准差的计算公式为:∑∑==-=ki iki if f x x 112)(σ标准差与变量值的计量单位相同,其实际意义比较清楚。
因此,在对社会经济现象进行分析时主要使用标准差。
例如,根据表4-7中的数据,计算50个家庭住房面积的标准差。
计算过程见表。
某城市50个家庭住房面积标准差计算表根据上面的计算公式得:8.235028328)(112==-=∑∑==ki iki if f x x σ(平方米) 结果表明,每个家庭的住房面积与平均数相比,平均相差23.8平方米。
3.离散系数上面介绍的标准差是反映数据分散程度的绝对值,其数值的大小一方面取决于原变量值本身水平高低的影响,也就是与变量的均值大小有关,变量值绝对水平高的,离散程度的测度值自然也就大,绝对水平小的离散程度的测度值自然也就小;另一方面,它们与原变量值的计量单位相同,采用不同计量单位计量的变量值,其离散程度的测度值也就不同。
因此,对于平均水平不同或计量单位不同的几组数据,是不能用上述离散程度的测度值直接比较其离散程度的。
为消除变量值水平高低和计量单位不同对离散程度测度值的影响,需要计算离散系数。
离散系数通常是就标准差来计算的,因此也称为标准差系数,它是一组数据的标准差与其相应的均值之比,是测度数据离散程度的相对指标,其计算公式为:xV σσ=离散系数的作用主要是用于比较对不同组别数据的离散程度。
离散系数大的说明数据的离散程度也就大,离散系数小的说明数据的离散程度也就小。
例如,某集团公司所属的8家子公司,其产品销售数据如表。
试比较产品销售额与销售利润的离散程度。
需要计算离散系数。
由表中数据计算得:1x =536.25(万元) 1σ=289.22(万元) 539.025.53622.2891==V2x =32.5215(万元) 2σ=21.60(万元) 664.05125.3260.212==V计算结果表明,21V V ,说明产品销售额的离散程度小于销售利润的离散程度。