模糊关系矩阵的定义和计算方法通常采用笛卡尔积算子

第2章 模糊矩阵与模糊关系2.1 模糊矩阵定义及其运算定义：一个矩阵内所有元素均在[0，1]闭区间内取值的矩阵，称为模糊矩阵并、交、补运算：两个模糊矩阵对应元素取大（取小、取补）作为新元素的矩阵，称为它们的并（交、补）运算 例：⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡∧∧∧∧=⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡∨∨∨∨=⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡=2.06.03.04.00.82.00.69.00.35.00.47.0B R 8.09.05.07.00.82.00.69.00.35.00.47.0B R 8.06.03.00.4B 2.09.05.07.0R C 0.70.50.30.5R 10.90.20.10.8⎡⎤⎡⎤=-=⎢⎥⎢⎥⎣⎦⎣⎦运算性质：注意不满足互补律2.2 模糊矩阵的截矩阵模糊矩阵截矩阵，类似于模糊集的截集例如： 0.70.8R 0.91⎡⎤=⎢⎥⎣⎦的0.7截矩阵为0.701R 11⎡⎤=⎢⎥⎣⎦ 不难看出，模糊矩阵的截矩阵必然是布尔矩阵。

2.3 模糊矩阵的合成运算模糊矩阵的合成运算类同于普通矩阵的乘法运算，只需将普通矩阵中的乘法运算和加法运算分别改为取小和取大运算即可。

例如：0.20.50.60.5Q R 0.70.10.41(0.20.6)(0.50.4)(0.20.5)(0.51)0.40.5Q R (0.70.6)(0.10.4)(0.70.5)(0.11)0.60.5⎡⎤⎡⎤==⎢⎥⎢⎥⎣⎦⎣⎦∧∨∧∧∨∧⎡⎤⎡⎤==⎢⎥⎢⎥∧∨∧∧∨∧⎣⎦⎣⎦性质：注意对交运算不满足分配律。

2.4 模糊矩阵的转置模糊矩阵的转置：类同于普通矩阵的转置。

T T c T T c (R )R, (R )(R )==2.5 模糊关系的定义及其运算1. 定义：X 与Y 直积(){},|, X Y x y x X y Y ⨯=∈∈中一个模糊子集R ，称为从X到Y 的模糊关系，记为R X Y →。

下面研究某一地区人的身高与体重的模糊关系：人的身高与体重X ，Y 的论域分别为：1234512345{,,,,}, {,,,,}X x x x x x Y y y y y y ==它们之间构成的模糊关系R表示论域X 中的元素i x 和论域Y 中的元素j y 对于关系R的隶属程度,R i j ij x y r μ=（）。

模糊算法的算子
模糊算法是一种基于模糊逻辑的计算方法，它可以处理模糊信息，使得计算结果更加准确。

在模糊算法中，算子是一种基本的运算符号，它可以用来表示模糊逻辑中的各种运算。

1. 模糊交算子
模糊交算子是模糊逻辑中的一种基本运算符号，它用来表示两个模糊集合之间的交集运算。

在模糊交算子中，两个模糊集合的交集结果是一个新的模糊集合，它的隶属度函数是两个原始模糊集合隶属度函数的最小值。

2. 模糊并算子
模糊并算子是模糊逻辑中的一种基本运算符号，它用来表示两个模糊集合之间的并集运算。

在模糊并算子中，两个模糊集合的并集结果是一个新的模糊集合，它的隶属度函数是两个原始模糊集合隶属度函数的最大值。

3. 模糊补算子
模糊补算子是模糊逻辑中的一种基本运算符号，它用来表示一个模糊集合的补集运算。

在模糊补算子中，一个模糊集合的补集结果是一个新的模糊集合，它的隶属度函数是原始模糊集合隶属度函数的补数。

4. 模糊积算子
模糊积算子是模糊逻辑中的一种基本运算符号，它用来表示两个模糊集合之间的积运算。

在模糊积算子中，两个模糊集合的积结果是一个新的模糊集合，它的隶属度函数是两个原始模糊集合隶属度函数的乘积。

5. 模糊除算子
模糊除算子是模糊逻辑中的一种基本运算符号，它用来表示两个模糊集合之间的除运算。

在模糊除算子中，两个模糊集合的除结果是一个新的模糊集合，它的隶属度函数是两个原始模糊集合隶属度函数的商。

模糊算法的算子是模糊逻辑中的基本运算符号，它们可以用来表示各种模糊运算，从而实现对模糊信息的处理和分析。

在实际应用中，模糊算法的算子可以用来解决各种模糊问题，如模糊控制、模糊决策等。

关于模糊关系与模糊子群的注记模糊关系和模糊子群是模糊数学中的两个重要概念，它们在各个领域中都有着广泛的应用。

本文将对这两个概念进行详细讨论，并介绍其相关的性质和应用。

一、模糊关系模糊关系是指一种不确定性的关系，它通常用来描述两个或多个对象之间的某种程度的关联性。

在模糊关系中，每个对象都被赋予了一个模糊度，表示其与其他对象的关系的不确定程度。

例如，在描述人与人之间的关系时，我们可以使用模糊关系来表示两个人之间的亲密程度、朋友关系等。

在模糊关系中，我们通常使用模糊矩阵来表示。

模糊矩阵是一个n×n的矩阵，其中每个元素都是一个[0,1]之间的实数，表示两个对象之间的模糊关系的强度。

如果两个对象之间的模糊关系越强，那么它们之间的模糊矩阵元素就越接近于1；反之，如果它们之间的关系越弱，那么元素就越接近于0。

模糊关系的应用非常广泛，例如在社交网络分析、人际关系建立、图像处理等领域都有着重要的应用。

在社交网络分析中，我们可以使用模糊关系来描述人与人之间的社交关系，从而分析社交网络的结构和特征。

在图像处理中，我们可以使用模糊关系来进行图像分割和图像识别等工作。

二、模糊子群模糊子群是指在一个群中的一个子集，它具有一定的模糊性质。

在模糊子群中，每个元素都被赋予了一个模糊度，表示它与子群中的其他元素的关系的不确定程度。

例如，在描述一个人群中的子群时，我们可以使用模糊子群来表示某些人之间的某种程度的关联性。

在模糊子群中，我们通常使用模糊子群矩阵来表示。

模糊子群矩阵是一个n×n的矩阵，其中每个元素都是一个[0,1]之间的实数，表示子群中两个元素之间的模糊关系的强度。

如果两个元素之间的模糊关系越强，那么它们之间的模糊子群矩阵元素就越接近于1；反之，如果它们之间的关系越弱，那么元素就越接近于0。

模糊子群的应用也非常广泛，例如在人际关系建立、图像处理、数据挖掘等领域都有着重要的应用。

在人际关系建立中，我们可以使用模糊子群来描述某些人之间的某种程度的关联性，从而为社交网络分析提供基础。

几种典型的模糊推理方法根据模糊推理的定义可知，模糊推理的结论主要取决于模糊蕴含关系),(~Y X R 及模糊关系与模糊集合之间的合成运算法则。

对于确定的模糊推理系统，模糊蕴含关系),(~Y X R 一般是确定的，而合成运算法则并不唯一。

根据合成运算法则的不同，模糊推理方法又可分为Mamdani 推理法、Larsen 推理法、Zadeh 推理法等等。

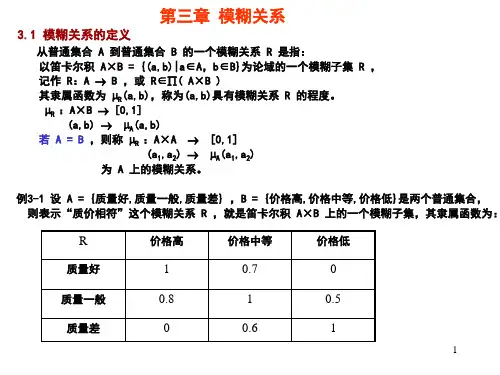
一、Mamdani 模糊推理法Mamdani 模糊推理法是最常用的一种推理方法，其模糊蕴涵关系),(~Y X R M 定义简单，可以通过模糊集合A ~和B ~的笛卡尔积(取小)求得，即)()(),(~~~y x y x B A RMμμμΛ= (3.2.1) 例 3.2.1 已知模糊集合3211.04.01~x x x A ++=，33211.03.05.08.0~y y y y B +++=。

求模糊集合A ~和B ~之间的模糊蕴含关系),(~Y X R M 。

解：根据Mamdani 模糊蕴含关系的定义可知：⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⨯=1.01.01.01.01.03.04.04.01.03.05.08.0]1.03.05.08.0[1.04.01~~),(~οB A Y X R MMamdani 将经典的极大—极小合成运算方法作为模糊关系与模糊集合的合成运算法则。

在此定义下，Mamdani 模糊推理过程易于进行图形解释。

下面通过几种具体情况来分析Mamdani 模糊推理过程。

(i) 具有单个前件的单一规则设*~A 和A ~论域X 上的模糊集合，B ~是论域Y 上的模糊集合，A ~和B ~间的模糊关系是),(~Y X R M ，有大前提(规则)： if x is A ~ then y is B ~小前提(事实)： x is *~A结论： y is ),(~~~**Y X R A B M ο=当)()(),(~~~y x y x B A RMμμμΛ=时，有 )()}()]()({[V )]}()([)({V )(~~~~Xx ~~~Xx ~***y y x x y x x y BB A AB A AB μωμμμμμμμΛ=ΛΛ=ΛΛ=∈∈ (3.2.2)其中)]()([V ~~Xx *x x AA μμωΛ=∈，称为A ~和*~A 的适配度。

第2章 模糊矩阵与模糊关系2.1 模糊矩阵定义及其运算定义：一个矩阵内所有元素均在[0，1]闭区间内取值的矩阵，称为模糊矩阵 并、交、补运算：两个模糊矩阵对应元素取大（取小、取补）作为新元素的矩阵，称为它们的并（交、补）运算 例：⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡∧∧∧∧=⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡∨∨∨∨=⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡=2.06.03.04.00.82.00.69.00.35.00.47.0B R 8.09.05.07.00.82.00.69.00.35.00.47.0B R 8.06.03.00.4B 2.09.05.07.0RC0.70.50.30.5R 10.90.20.10.8⎡⎤⎡⎤=-=⎢⎥⎢⎥⎣⎦⎣⎦运算性质：注意不满足互补律2.2 模糊矩阵的截矩阵模糊矩阵截矩阵，类似于模糊集的截集例如： 0.70.8R 0.91⎡⎤=⎢⎥⎣⎦的0.7截矩阵为0.701R 11⎡⎤=⎢⎥⎣⎦ 不难看出，模糊矩阵的截矩阵必然是布尔矩阵。

2.3 模糊矩阵的合成运算模糊矩阵的合成运算类同于普通矩阵的乘法运算，只需将普通矩阵中的乘法运算和加法运算分别改为取小和取大运算即可。

例如：0.20.50.60.5Q R 0.70.10.41(0.20.6)(0.50.4)(0.20.5)(0.51)0.40.5Q R (0.70.6)(0.10.4)(0.70.5)(0.11)0.60.5⎡⎤⎡⎤==⎢⎥⎢⎥⎣⎦⎣⎦∧∨∧∧∨∧⎡⎤⎡⎤==⎢⎥⎢⎥∧∨∧∧∨∧⎣⎦⎣⎦性质：注意对交运算不满足分配律。

2.4 模糊矩阵的转置模糊矩阵的转置：类同于普通矩阵的转置。

T T c T T c (R )R, (R )(R )==2.5 模糊关系的定义及其运算1. 定义：X 与Y 直积 (){},|, X Y x y x X y Y ⨯=∈∈中一个模糊子集R ，称为从X到Y 的模糊关系，记为RX Y →。

下面研究某一地区人的身高与体重的模糊关系：某地区人身高与体重相互关系构成一个模糊关系乙丙 甲叔侄关系 父子关系R弟兄关系QS=Q ο R2.1 模糊关系是普通关系的推广人的身高与体重X ，Y 的论域分别为：1234512345{,,,,}, {,,,,}X x x x x x Y y y y y y ==它们之间构成的模糊关系R 表示论域X 中的元素i x 和论域Y 中的元素j y 对于关系R 的隶属程度,R i j ij x y r μ=（）。

几种典型的模糊推理方法根据模糊推理的定义可知，模糊推理的结论主要取决于模糊蕴含关系),(~Y X R 及模糊关系与模糊集合之间的合成运算法则。

对于确定的模糊推理系统，模糊蕴含关系),(~Y X R 一般是确定的，而合成运算法则并不唯一。

根据合成运算法则的不同，模糊推理方法又可分为Mamdani 推理法、Larsen 推理法、Zadeh 推理法等等。

一、Mamdani 模糊推理法Mamdani 模糊推理法是最常用的一种推理方法，其模糊蕴涵关系),(~Y X R M 定义简单，可以通过模糊集合A ~和B ~的笛卡尔积(取小)求得，即)()(),(~~~y x y x B A RMμμμΛ= (3.2.1)例 3.2.1 已知模糊集合3211.04.01~x x x A ++=，33211.03.05.08.0~y y y y B +++=。

求模糊集合A ~和B ~之间的模糊蕴含关系),(~Y X R M 。

解：根据Mamdani 模糊蕴含关系的定义可知：⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⨯=1.01.01.01.01.03.04.04.01.03.05.08.0]1.03.05.08.0[1.04.01~~),(~ B A Y X R MMamdani 将经典的极大—极小合成运算方法作为模糊关系与模糊集合的合成运算法则。

在此定义下，Mamdani 模糊推理过程易于进行图形解释。

下面通过几种具体情况来分析Mamdani 模糊推理过程。

(i) 具有单个前件的单一规则设*~A 和A ~论域X 上的模糊集合，B ~是论域Y 上的模糊集合，A ~和B ~间的模糊关系是),(~Y X R M ，有大前提(规则)： if x is A ~then y is B ~小前提(事实)： x is *~A结论： y is ),(~~~**Y X R A B M =当)()(),(~~~y x y x B A RMμμμΛ=时，有)()}()]()({[V )]}()([)({V )(~~~~Xx ~~~Xx ~***y y x x y x x y BB A AB A AB μωμμμμμμμΛ=ΛΛ=ΛΛ=∈∈ (3.2.2)其中)]()([V ~~Xx *x x AA μμωΛ=∈，称为A ~和*~A 的适配度。

构造模糊矩阵什么是模糊矩阵模糊矩阵是一种数学工具，用于描述事物之间的模糊关系。

在传统的矩阵计算中，每个元素只能取一个确定的值，而在模糊矩阵中，每个元素可以取一个模糊的值，即在一个模糊度范围内的任意值。

模糊矩阵常用于描述模糊关系、模糊规则等。

如何构造模糊矩阵构造模糊矩阵的关键是确定每个元素的模糊程度，一般可以通过以下几种方式来进行：1. 主观评价法主观评价法是一种基于主观意见的构造模糊矩阵的方法。

在这种方法中，我们根据自己的经验、知识或直觉，给出每个元素的模糊程度。

通常可以使用模糊语言（如“非常模糊”、“模糊”、“不模糊”等）或数值（如0-1之间的模糊程度）来表示。

据自己对天气的观察和感受，给出每种天气状况的模糊程度，如下所示：晴天雨天多云晴天10.80.5雨天0.810.6多云0.50.612. 统计分析法统计分析法是一种基于数据分析的构造模糊矩阵的方法。

在这种方法中，我们根据已有的数据进行统计分析，得出每个元素的模糊程度。

通过收集顾客的评价数据，统计分析得出每个元素的模糊程度，如下所示：满意一般不满意满意10.60.3一般0.610.7不满意0.30.713. 模糊测度法模糊测度法是一种基于模糊测度的构造模糊矩阵的方法。

在这种方法中，我们先确定每个元素的隶属函数，再通过隶属函数计算得出每个元素的模糊程度。

例如，我们想构造一个描述温度大小的模糊矩阵。

可以先确定每个元素的隶属函数，如下所示：•隶属函数“低温”：温度在10℃以下隶属度为1，随着温度升高，隶属度逐渐减小；•隶属函数“中等温度”：温度在10℃到20℃之间隶属度为1，随着温度升高或降低，隶属度逐渐减小；•隶属函数“高温”：温度在20℃以上隶属度为1，随着温度降低，隶属度逐渐减小。

然后，根据隶属函数计算得出每个元素的模糊程度，如下所示：低温中等温度高温低温10.50.2中等温度0.510.7高温0.20.71总结构造模糊矩阵是一种描述事物之间模糊关系的有效方法。

第2章 模糊矩阵与模糊关系2.1 模糊矩阵定义及其运算定义：一个矩阵内所有元素均在[0，1]闭区间内取值的矩阵，称为模糊矩阵并、交、补运算：两个模糊矩阵对应元素取大（取小、取补）作为新元素的矩阵，称为它们的并（交、补）运算 例：⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡∧∧∧∧=⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡∨∨∨∨=⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡=2.06.03.04.00.82.00.69.00.35.00.47.0B R 8.09.05.07.00.82.00.69.00.35.00.47.0B R 8.06.03.00.4B 2.09.05.07.0R C 0.70.50.30.5R 10.90.20.10.8⎡⎤⎡⎤=-=⎢⎥⎢⎥⎣⎦⎣⎦运算性质：注意不满足互补律2.2 模糊矩阵的截矩阵模糊矩阵截矩阵，类似于模糊集的截集例如： 0.70.8R 0.91⎡⎤=⎢⎥⎣⎦的0.7截矩阵为0.701R 11⎡⎤=⎢⎥⎣⎦ 不难看出，模糊矩阵的截矩阵必然是布尔矩阵。

2.3 模糊矩阵的合成运算模糊矩阵的合成运算类同于普通矩阵的乘法运算，只需将普通矩阵中的乘法运算和加法运算分别改为取小和取大运算即可。

例如：0.20.50.60.5Q R 0.70.10.41(0.20.6)(0.50.4)(0.20.5)(0.51)0.40.5Q R (0.70.6)(0.10.4)(0.70.5)(0.11)0.60.5⎡⎤⎡⎤==⎢⎥⎢⎥⎣⎦⎣⎦∧∨∧∧∨∧⎡⎤⎡⎤==⎢⎥⎢⎥∧∨∧∧∨∧⎣⎦⎣⎦性质：注意对交运算不满足分配律。

2.4 模糊矩阵的转置模糊矩阵的转置：类同于普通矩阵的转置。

T T c T T c (R )R, (R )(R )==2.5 模糊关系的定义及其运算1. 定义：X 与Y 直积 (){},|, X Y x y x X y Y ⨯=∈∈中一个模糊子集R ，称为从X到Y 的模糊关系，记为RX Y →。

下面研究某一地区人的身高与体重的模糊关系：人的身高与体重X ，Y 的论域分别为：1234512345{,,,,}, {,,,,}X x x x x x Y y y y y y ==它们之间构成的模糊关系R 表示论域X 中的元素i x 和论域Y 中的元素j y 对于关系R 的隶属程度,R i j ij x y r μ=（）。

第2章 模糊矩阵与模糊关系2.1 模糊矩阵定义及其运算定义：一个矩阵内所有元素均在[0，1]闭区间内取值的矩阵，称为模糊矩阵 并、交、补运算：两个模糊矩阵对应元素取大（取小、取补）作为新元素的矩阵，称为它们的并（交、补）运算 例：⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡∧∧∧∧=⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡∨∨∨∨=⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡=2.06.03.04.00.82.00.69.00.35.00.47.0B R 8.09.05.07.00.82.00.69.00.35.00.47.0B R 8.06.03.00.4B 2.09.05.07.0RC0.70.50.30.5R 10.90.20.10.8⎡⎤⎡⎤=-=⎢⎥⎢⎥⎣⎦⎣⎦运算性质：注意不满足互补律2.2 模糊矩阵的截矩阵模糊矩阵截矩阵，类似于模糊集的截集例如： 0.70.8R 0.91⎡⎤=⎢⎥⎣⎦的0.7截矩阵为0.701R 11⎡⎤=⎢⎥⎣⎦ 不难看出，模糊矩阵的截矩阵必然是布尔矩阵。

2.3 模糊矩阵的合成运算模糊矩阵的合成运算类同于普通矩阵的乘法运算，只需将普通矩阵中的乘法运算和加法运算分别改为取小和取大运算即可。

例如：0.20.50.60.5Q R 0.70.10.41(0.20.6)(0.50.4)(0.20.5)(0.51)0.40.5Q R (0.70.6)(0.10.4)(0.70.5)(0.11)0.60.5⎡⎤⎡⎤==⎢⎥⎢⎥⎣⎦⎣⎦∧∨∧∧∨∧⎡⎤⎡⎤==⎢⎥⎢⎥∧∨∧∧∨∧⎣⎦⎣⎦性质：注意对交运算不满足分配律。

2.4 模糊矩阵的转置模糊矩阵的转置：类同于普通矩阵的转置。

T T c T T c (R )R, (R )(R )==2.5 模糊关系的定义及其运算1. 定义：X 与Y 直积 (){},|, X Y x y x X y Y ⨯=∈∈中一个模糊子集R ，称为从X到Y 的模糊关系，记为RX Y →。

下面研究某一地区人的身高与体重的模糊关系：某地区人身高与体重相互关系构成一个模糊关系乙丙甲叔侄关系 父子关系R弟兄关系QS=QR S=QR2.1 模糊关系是普通关系的推广人的身高与体重X ，Y 的论域分别为：1234512345{,,,,}, {,,,,}X x x x x x Y y y y y y ==它们之间构成的模糊关系R 表示论域X 中的元素i x 和论域Y 中的元素j y 对于关系R 的隶属程度,R i j ij x y r μ=（）。