截面几何性质-T形截面

第七章平面图形的几何性质研究截面几何性质的意义从上章介绍的应力和变形的计算公式中可以看出，应力和变形不仅与杆的内力有关，而且与杆件截面的横截面面积A、极惯性矩I P、抗扭截面系数W P等一些几何量密切相关。

因此要研究构件的的承载能力或应力，就必须掌握截面几何性质的计算方法。

另一方面，掌握截面的几何性质的变化规律，就能灵活机动地为各种构件选取合理的截面形状和尺寸，使构件各部分的材料能够比较充分地发挥作用，尽可能地做到“物尽其用”，合理地解决好构件的安全与经济这一对矛盾。

第一节 静矩一、静距的概念Ay S z d d =Az S y d d =⎰⎰⎰⎰====AAy y AAz z Az S S A y S S d d d d zy d A yz静距是面积与它到轴的距离之积。

平面图形的静矩是对一定的坐标而言的，同一平面图形对不同的坐标轴，其静矩显然不同。

静矩的数值可能为正，可能为负，也可能等于零。

它常用单位是m 3或mm 3。

形心d A zyy zCx Cy ⎪⎪⎭⎪⎪⎬⎫⋅∆∑=⋅∆∑=A y A y Az A z C C ⎪⎪⎭⎪⎪⎬⎫==⎰⎰A ydA y A zdA z AC A C ⎪⎪⎭⎪⎪⎬⎫==A S y A S z z C y C ⎭⎬⎫⋅=⋅=C y C z z A S y A S 平面图形对z 轴（或y 轴）的静矩，等于该图形面积A 与其形心坐标y C （或z C ）的乘积。

当坐标轴通过平面图形的形心时，其静矩为零；反之，若平面图形对某轴的静矩为零，则该轴必通过平面图形的形心。

如果平面图形具有对称轴，对称轴必然是平面图形的形心轴，故平面图形对其对称轴的静矩必等于零。

⎭⎬⎫⋅=⋅=C y C z z A S y A S二、组合图形的静矩根据平面图形静矩的定义，组合图形对z 轴（或y 轴）的静矩等于各简单图形对同一轴静矩的代数和，即⎪⎪⎭⎪⎪⎬⎫=+++==+++=∑∑==ni Ci i Cn n C C y ni Ci i Cn n C C z z A z A z A z A S y A y A y A y A S 1221112211 式中 y Ci 、z Ci 及A i 分别为各简单图形的形心坐标和面积;n 为组成组合图形的简单图形的个数。

钢结构的连接习题及答案例 3.1试验算图3-21 所示钢板的对接焊缝的强度。

钢板宽度为200mm ，板厚为14mm ，轴心拉力设计值为N=490kN ，钢材为Q235 ，手工焊，焊条为E43 型，焊缝质量标准为三级，施焊时不加引弧板。

（a）（b）图 3-21 例题 3-1（a）正缝；（ b）斜缝解：焊缝计算长度l w200 214 172mm焊缝正应力为490103203.5N / mm 2w185N / mm217214 f t不满足要求，改为斜对接焊缝。

取焊缝斜度为 1.5：1，相应的倾角56 0,焊缝长度l w'200214213.2mmsin 56 0此时焊缝正应力为N sin490103sin 5602w185N / mm 2l w't213.214136.1N / mmf f剪应力为N cos490103 cos56091.80N / mm2 f v w125N / mm2l w' t213.214斜焊缝满足要求。

tg 560 1.48 ，这也说明当 tg 1.5 时，焊缝强度能够保证，可不必计算。

例 3.2 计算图3-22 所示T 形截面牛腿与柱翼缘连接的对接焊缝。

牛腿翼缘板宽130mm，厚 12mm ，腹板高200mm，厚 10mm 。

牛腿承受竖向荷载设计值V=100kN ，力作用点到焊缝截面距离e=200mm。

钢材为 Q345，焊条E50 型，焊缝质量标准为三级，施焊时不加引弧板。

解：将力 V 移到焊缝形心，可知焊缝受剪力V=100kN ，弯矩M Ve1000.2 20kN m 翼缘焊缝计算长度为130212106mm腹板焊缝计算长度为200 10190mm（a）（b）图 3-22 例题 3-2（a）T 形牛腿对接焊缝连接；（ b）焊缝有效截面焊缝的有效截面如图3-22b 所示，焊缝有效截面形心轴x x 的位置y110.6 1.20.619 1.010.76.65cm10.6 1.219 1.0y219 1.2 6.6513.55cm焊缝有效截面惯性矩I x119319 1 4.05210.6 1.2 6.0521349cm412翼缘上边缘产生最大拉应力，其值为My120106 6.65102f t w2t I x134910498.59N / mm265N / mm 腹板下边缘压应力最大，其值为My2 2010613.55102w310N / mm 2a I x1349 104200.89N / mm f c为简化计算，认为剪力由腹板焊缝承受，并沿焊缝均匀分布V10010352.63N / mm2 f v w180N / mm2A w19010腹板下边缘正应力和剪应力都存在，验算该点折算应力232200.92352.632a220.6N / mm2 1.1 f t w 1.1265291.5N / mm2焊缝强度满足要求。

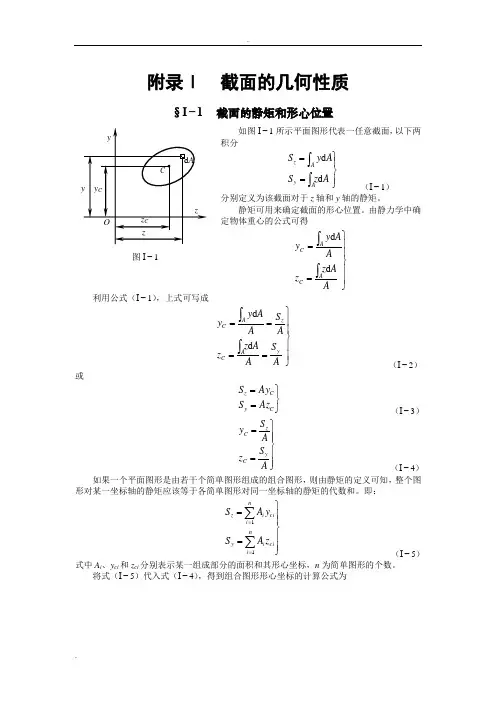
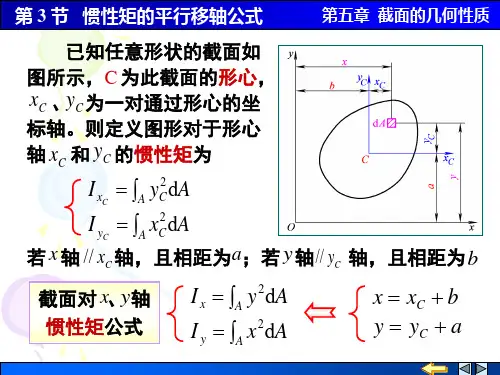
附录Ⅰ 截面的几何性质§I −1 截面的静矩和形心位置如图I −1所示平面图形代表一任意截面，以下两积分⎪⎭⎪⎬⎫==⎰⎰A z S A y S A y Az d d （I −1） 分别定义为该截面对于z 轴和y 轴的静矩。

静矩可用来确定截面的形心位置。

由静力学中确定物体重心的公式可得⎪⎪⎭⎪⎪⎬⎫==⎰⎰A A z z A A y y AC ACd d利用公式（I −1），上式可写成⎪⎪⎭⎪⎪⎬⎫====⎰⎰A S A A z z A S A Ay y y AC z AC d d （I −2） 或⎭⎬⎫==C y C z Az S Ay S （I −3）⎪⎪⎭⎪⎪⎬⎫==A S z A S y y C z C （I −4）如果一个平面图形是由若干个简单图形组成的组合图形，则由静矩的定义可知，整个图形对某一坐标轴的静矩应该等于各简单图形对同一坐标轴的静矩的代数和。

即：⎪⎪⎭⎪⎪⎬⎫==∑∑==ni ci i y ni ci i z z A S y A S 11（I −5）式中A i 、y ci 和z ci 分别表示某一组成部分的面积和其形心坐标，n 为简单图形的个数。

将式（I −5）代入式（I −4），得到组合图形形心坐标的计算公式为图I −1⎪⎪⎪⎪⎪⎭⎪⎪⎪⎪⎪⎬⎫==∑∑∑∑====n i i ni ci i c ni i ni ci i c A z A z A y A y 1111（I −6） 例题I −1 图a 所示为对称T 型截面，求该截面的形心位置。

解：建立直角坐标系zOy ，其中y 为截面的对称轴。

因图形相对于y 轴对称，其形心一定在该对称轴上，因此z C =0，只需计算y C 值。

将截面分成Ⅰ、Ⅱ两个矩形，则A Ⅰ=0.072m 2，A Ⅱ=0.08m 2 y Ⅰ=0.46m ，y Ⅱ=0.2m m323.008.0072.02.008.046.0072.0III IIII I I 11=+⨯+⨯=++==∑∑==A A y A y A AyA y ni ini cii c§I −2 惯性矩、惯性积和极惯性矩如图I −2所示平面图形代表一任意截面，在图形平面内建立直角坐标系zOy 。

文档《钢结构结构基本原理》试验课程作业L ENGINEERING钢结构基本原理试验报告试验名称T 形轴心受压柱的整体稳定试验试验课教师******学号****手机号**理论课教师*日期2012年11月21日一、试验目的1、了解T形截面轴心受压钢构件的整体稳定试验方法，包括试件设计、试验装置设计、测点布置、加载方式、试验结果整理与分析等。

2、观察T形截面轴心受压柱的失稳过程和失稳模式，加深对其整体稳定概念的理解。

3、将柱子理论承载力和实测承载力进行比较，加深对T形截面轴心受压构件整体稳定系数及其计算公式的理解。

二、试验原理轴心受压构件的可能破坏形式有强度破坏、整体失稳破坏和局部失稳等几种，其中整体失稳破坏时轴心受压构件的主要破坏形式。

对于理想压杆模型，即杆件是等截面压杆，压力作用线与截面形心纵轴重合，材料是完全均匀和弹性的，其整体稳定性能可用欧拉临界力或欧拉临界应力表征：然而对于实际构件而言，都带有多种初始缺陷，根据开口薄壁杆件理论，引入初始缺陷的轴心压杆的弹性微分方程为：我国规通过试验统计获得了四组柱子曲线：图2钢结构规柱子曲线对于T型截面压杆，其欧拉临界力为x,uy,v图1 ,T型截面示意图T形截面属于单轴对称截面，而且其对称轴为弱轴，因此，当不设置平面外支撑时，T 形截面轴心受压构件总是发生弯扭失稳。

稳定系数与承载力计算如下:对其弱轴x轴：换算长细比：力根据Perry公式T型截面压杆的稳定承载三、试验设计1、试件设计根据反力架的尺寸以及千斤顶的最大行程与加载能力，本实验设计的试件主要参数如下，试件截面（T形截面）h×b×t w×t f=60mm×600mm×5mm×5mm试件长度：L＝500mm钢材牌号：Q235B2、实验装置设计下图为进行工字形截面轴心受压构件整体稳定实验采用的实验装置，加载设备为千斤顶。

构件竖向放置，千斤顶于构件上端施加压力，荷载值由液压传感器测得。

T型截面极限屈服弯矩的计算是一个涉及到材料力学、结构分析和几何形状效应的问题。

在分析T型截面的极限屈服弯矩时，我们需要考虑截面的形状、尺寸、材料的性质以及荷载的作用方式等因素。

首先，T型截面是由一个矩形截面与一个圆形截面拼接而成的形状，这种截面在承受弯矩作用时，几何形状本身可能引起应力分布的改变。

其次，材料的性质也是决定弯矩承载能力的重要因素，不同材料的力学性能，如强度、塑性、韧性等，都会影响截面的极限屈服弯矩。

在确定T型截面极限屈服弯矩的过程中，我们需要考虑以下几个步骤：
1. 计算矩形部分和圆弧部分的应力分布，分别考虑各自的最小与最大应力值。

2. 考虑截面的尺寸，尤其是宽度和圆弧高度，它们会影响到应力集中的程度。

3. 考虑材料的性质，根据材料的力学性能，确定各部分材料的屈服强度和抗拉强度。

4. 在考虑荷载作用方式的基础上，分析截面是否能够承受弯矩的作用，判断是否达到极限状态。

具体计算方法可以采用有限元分析或有限强度折减系数法。

对于一般情况，我们可以根据经验公式进行估算：当梁的宽度较小时，其极限屈服弯矩可按矩形截面进行计算；当梁的宽度较大时，其有效宽度则按T型截面腹板进行计算。

对于T型截面高度的变化，则对极限屈服弯矩的影响较为显著。

总的来说，T型截面极限屈服弯矩的计算是一个复杂的过程，需要考虑多个因素的综合影响。

在实际应用中，我们需要根据具体情况进行分析和计算，以确保结构的可靠性和安全性。

以上回答仅供参考，希望对您有所帮助。