当前位置：文档之家 › 高一数学课件 三角函数

高一数学课件 三角函数

  • 格式：ppt
  • 大小：1.54 MB
  • 文档页数：17

下载文档原格式

  / 17

合集下载

高中数学高一必修第一章《三角函数的图象与性质》教育教学课件

高中数学高一必修第一章《三角函数的图象与性质》教育教学课件
点是 (0,0)，π2，1，(π，0)，32π，－1，(2π，0) ；
画余弦函数y＝cos x，x∈[0,2π]的图象，五个关键
点是(0,1)，π2，0，(π，－1)，32π，0，(2π，1) .
学习目标 要点疑点 深入探究 课堂检测
填要点·记疑点
3.正弦、余弦曲线的联系
根据引诱公式cos x＝sin x＋π2 ，要得到y＝cos x的
第一章 三角函数
§1.4 三角函数的图象与性质
MORESHI POWERPOINT 主讲老师：
CONTENTS
学习目标 要点疑点 深入探究 课堂检测
明目标、知重点
• 了解利用单位圆中的正弦线画正弦曲线的方法. • 掌控“五点法”画正弦曲线和余弦曲线的步骤和方法，能
用“五点法”作出简单的正弦、余弦曲线. • 理解正弦曲线与余弦曲线之间的联系.
学习目标 要点疑点 深入探究 课堂检测
明目标、知重点
摸索2 如何由y＝sin x，x∈[0,2π]的图象得到y＝sin x， x∈R的图象？ 答 由于终边相同的角有相同的三角函数值，所以函数y＝sin x，x∈[2kπ，2(k＋1)π)，k∈Z且k≠0的图象，与函数y＝sin x，x∈[0,2π)的图象的形状完全一致.于是我们只要将函数y＝ sin x，x∈[0,2π)的图象向左、向右平行移动(每次2π个单位 长度)，就可以得到正弦函数y＝sin x，x∈R的图象.
摸索2 如何用描点法画出y＝sin x，x∈[0,2π]的图象？
答 在精确度要求不太高时，y＝sin x，x∈[0,2π]可以通过找出 (0,0)， π2，1，(π，0)，32π，－1，(2π，0)五个关键点，再用光滑曲线将它们 连接起来，就可得 y＝sin x，x∈[0,2π]的图象，这种方法简称“五点法”.

5.2.1三角函数的概念课件高一数学(人教A版必修第一册)

5.2.1三角函数的概念课件高一数学(人教A版必修第一册)
【解析】射线 = − 3 < 0 经过第二象限，
在射线上的取点 −1, 3 ，
即角 的终边经过点 −1, 3 ，
则 =
−1
2
+
3
2
= 2，
利用三角函数定义可得
sin =


=
3
，cos
2
tan =


=
3
−1
3
2
所以sin =
=


=
−1
2
1
=− ，
2
= − 3；
1
, cos = − 2 , tan = − 3.

（3）在角− 的终边上取一点 , − ，即 = , = −, = ，



= − , −




（4）在角 的终边上取一点

则 −
则 =



,


=−
=

,

−


= −；
−, ，即 = −, = , = ，


当 = 或



时，点的坐标是(, )和(− ， )



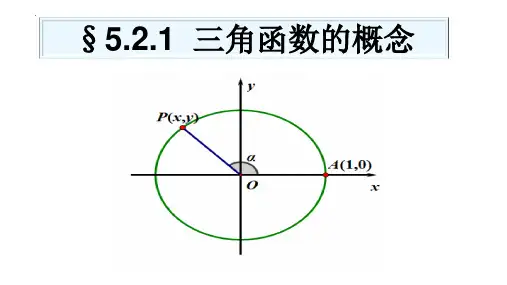
一般地，任意给定一个角，它的终边与单位圆交点的坐标能唯一确定吗？
∀ ∈ , 其终边与单位圆交点的横坐标, 纵坐标唯一确定.
新知1：三角函数的定义
（1）把点的纵坐标叫做的正弦函数，记作 ，
即 = .
π

转 3 弧度，滚珠 按顺时针方向每秒钟转 6 弧度，相遇后发生碰撞，各自按照原来的速度大小反向运动．
(1)求滚珠 ， 第一次相遇时所用的时间及相遇点的坐标；

高一数学人必修课件三角函数的积化和差与和差化积

高一数学人必修课件三角函数的积化和差与和差化积

180°。三角形内角和的应用 Nhomakorabea03
能够运用三角形内角和定理解决与三角形相关的角度、边长等
问题。
05
三角函数在物理中应用
振动与波动问题
简谐振动
描述物体在平衡位置附近的往复 运动，其位移与时间的关系可用
三角函数表示。
机械波
介质中质点振动的传播，波动方 程中包含三角函数，用于描述波 的传播特性和质点的振动状态。
诱导公式及其应用
诱导公式
通过角度的加减、倍角等运算，将复杂角度的三角函数转化为基本角度的三角函 数进行计算。常见的诱导公式有和差化积公式、积化和差公式、倍角公式等。
应用
诱导公式在三角函数计算中具有重要的应用，可以简化计算过程，提高计算效率 。例如，利用和差化积公式可以将两个角度的三角函数之和或差转化为单个角度 的三角函数进行计算。
具体推导过程如下：首先，根据三角 函数的加减化积公式，我们有 sin(a+b)=sinacosb+cosasinb和 cos(a+b)=cosacosb−sinasinb。
最后，通过观察和比较这两个表达式 ，我们可以发现和差化积公式的形式 。
公式应用举例
01
02
03
04
已知sinα=3/5,cosβ=−4/5， 且α,β为钝角，求cos(α+β)的
周期性、奇偶性与单调性
周期性
正弦函数、余弦函数具有周期性 ，周期$T = 2pi$；正切函数、余 切函数也具有周期性，周期$T =
pi$。
奇偶性
正弦函数是奇函数，余弦函数是偶 函数；正切函数、余切函数既不是 奇函数也不是偶函数。
单调性
正弦函数、余弦函数在各自周期内 具有单调性；正切函数、余切函数 在各自定义域内不具有单调性。

高一数学人教A版必修一5.2.2同角三角函数的基本关系课件

高一数学人教A版必修一5.2.2同角三角函数的基本关系课件

cos 5 4 4
如果α是第四象限角,那么 cos 4 , tan 3
5
4
例3、 已 知tan 3，为 第 三 象 限 角 ， 求sin ,cos的 值 。
4
联 立 方 程 组
tan sin cos
方程(组)思想
si n2 cos2 1
练 习1、 已 知sin cos 5 ，180 270， 求tan的 值 。
5
所 以tan sin 2 cos
类型二：应用同角三角函数的基本关系化简三角函数式
例4、 化 简(：1) sin cos tan 1
切化弦
si n si n
co s
1
co s
si n si n
cos cos
2cos2 1
(2)
1 2sin2
“1”的代换
2cos2 (sin2 cos2 )
(2)求
s
i
n2 5
si
sin cos n cos si
n2
3co
s2 1
(3)求2sin2 sin cos 3cos2
小结 1、同角三角函数的基本关系
平方关系: sin2 cos2 1
商数关系: tan si n ( k , k Z )
cos
2
2、已知sinα(或cosα)求其它
4
3
例2、 已 知sin 3 ,求cos , tan的 值 。
5
解：因为sinα<0，sinα≠-1, 所以α是第三或第四象限角
由sin2α+cos2α=1得 cos2 1 sin2 1 ( 3)2 16 .
5 25
如果α是第三象限角,那么 cos 16 4

三角函数的概念高一数学精讲课件

三角函数的概念高一数学精讲课件

则 PM y , P0M 0 y0 ，OM x ,OM 0 x0 ,
OMP OM0P0.
所以得到 P0M0 PM ,
1r
即 y0
y.
r
因为
y与
y0 同号，所以
y0
y r
，即sin
y.
r
同理可证：cos x ，tan y .
r
x
PART 2 三角函数值的正负
根据三角函数的定义，请将三角函数值的符号填入下图：
所以tan 672 0；
（3）因为3 2，所以3角的终边位于 x轴的非正半轴上， 所以tan3 0.
练习.已知半径为120mm的圆上，有一条弧的长是 144mm，求该弧所对的圆心角(正角)的弧度数
3
2 1 0 1 2 3 -1
2 22
222
tana 0
3 3
1
3
/
3
-1 3 0
3
例题探究
例3. 确定下列三角函数的符号 （1）sin250° （2）tan(-672°) （3）tan3π
解：（1）因为250 是第三象限角，所以sin 250 0； （2）因为672 48 360 2，所以672 角的终边与48
() ( )
y
() ( )
O
x
() ( )
O
x
() ( )
O
x
() ( )
PART 3 特殊角的三角函数值
角α 0° 30° 45° 60° 90° 120° 135° 150° 180°
弧度 0
6
sina 0 1 2
432
2 31
22
2 3 5
3 46
3 21 0 2 22

高一数学 三角函数图象---正弦、余弦、正切函数图象 ppt课件

高一数学 三角函数图象---正弦、余弦、正切函数图象 ppt课件

y
1
● ●
0 -1
2

●
3 2
●
2
●
x
练习：用“五点画图法”画出正弦函数
y=sinx(x

[0, 2 ]的图象
三、余弦函数y=cosx(xR)的图象
sin(
x+ 2
y 1
)= cosx
y=sinx的图象
2
0 2
-1
2
3 2
2
3
4
5
6
x
y=cosx的图象
三角函数图象
---正弦、余弦、正切函数图象
§4.8正弦函数、余弦函数的图象和性质
正弦函数y=sinx和余弦函数y=cosx图象的画法
1、描点法 2、几何法
复习：三角函数线
的终边
P 1
y
正弦线——OM 余弦线——MP 正切线——OT
A 1
-1
M
o
x
-1 T
一、正弦函数y=sinx（x R)的图象
y 1
y=sinx (xR)

2
2

-1
0
3
4
5
6
x
二、正弦函数的“五点画图法”
(0,0)、( , 1)、( 2
y 1
● ●

3 ,0)、( 2
,-1)、 (2 ,0)
0
2

●
3 2
●
2
●
x
-1
小结：五点作图法的步骤：1、找出起关键作用的这五个点：
即最高点和最低点以及平衡点在坐标轴上把它们描出来；2、 用平滑的曲线把它们连接起来，就可以把它的大致图象画出来 了。

高一数学必修四课件第章三角函数的周期性

高一数学必修四课件第章三角函数的周期性

研究三角函数周期性的意义
理解周期性现象
三角函数是描述周期性现象的重要数 学模型，研究其周期性有助于深入理 解这类现象的本质。
简化计算过程
拓展数学知识体系
三角函数周期性是数学分析、复变函 数等后续课程的基础内容之一，掌握 好这部分内容有助于后续课程的学习 。
利用三角函数的周期性，可以将复杂 的问题转化为简单的问题进行处理， 从而简化计算过程。
高一数学必修四课件第章三 角函数的周期性
汇报人：XX 2024-01-20
contents
目录
• 三角函数周期性概述 • 正弦函数与余弦函数的周期性 • 正切函数与余切函数的周期性 • 三角函数周期性的应用 • 三角函数周期性的拓展与延伸
01 三角函数周期性 概述
周期函数定义
周期函数的定义
对于函数$y = f(x)$，如果存在一个正数$T$，使得对于任意$x$都有$f(x + T) = f(x)$，则称$y = f(x)$为周期函数，$T$为它的周期。
相位差
正切函数和余切函数的图像之间存在相位差，即cot(x) = tan(π/2 - x)。这表明在相同的周期内，正切函数和余切 函数的图像可以通过平移相互转换。
周期性应用
由于正切函数和余切函数具有周期性，因此在实际应用中 可以利用这一性质解决一些与周期性相关的问题，如波动 、振动等。
04 三角函数周期性 的应用
期性的关系。
利用三角函数周期性建立振动和 波动问题的数学模型，进行定量
计算。
在信号处理中的应用
将信号分解为不同频 率的正弦波或余弦波 ，实现信号的频谱分 析。
通过三角函数周期性 对信号进行滤波、降 噪等处理，提高信号 质量。

高一数学必修第一册正弦函数、余弦函数的性质课件

高一数学必修第一册正弦函数、余弦函数的性质课件

上都单调递减，其值从1减小到-1.
最大值与最小值
【整理】从上述对正弦函数、余弦函数的单调性的讨论中容易得到：

+ ( ∈ ) 时取得最大值1，


当且仅当 = − + ( ∈ ) 时取得最小值-1；

①正弦函数当且仅当 =
②余弦函数当且仅当 = ( ∈ ) 时取得最大值1，
【1】周期性：观察正弦函数的图像，可以发现，在图像上，横坐标每隔2π个单位
长度，就会出现纵坐标相同的点，这就是正弦函数值具有的“周而复始”的
变化规律.实际上，这一点既可以从定义中看出，也能从诱导公式中得到反映.即自
变量 的值加上2π的整数倍时所对应的函数值，与 所对应的函数值相等.数学
上用周期性来定量地刻画这种“周而复始”的规律.
如何用自变量的系数表示上述函数的周期呢？
事实上，令 = + ，那么由 ∈ 得 ∈ ，且函数 = , ∈ 及函数
= , ∈ 的周期都是.
因为 + = + + = +




+ ，所以自变量增加 ，函数值




+ ,
+ ( ∈ ) 上都单调递减，其值从1减小到-1.


单调性


−
−



−



同样的道理结合余弦函数的周期性我们可以知道：
余弦函数在每一个闭区间
在每一个闭区间
− + , ( ∈ ) 上都单调递增，其值从-1增大到1；
, + ( ∈ )
关于y轴对称.所以正弦函数是奇函数，余弦函数是偶函数.

高一数学1[1].2.1任意角三角函数_教学课件

高一数学1[1].2.1任意角三角函数_教学课件
y 4 4 tan α = = = . x 3 3
主页
x
P0
1. 2. 1任意角的三角函数 (一) 任意角的三角函数 一
的终边过点P(【2】已知角 的终边过点 -12, 5), 则 】已知角θ的终边过点
5 sin θ = _____; 13
12 cos θ = _____; 13
5 tan θ = _____ . 12
求角α 例2.已知角 终边经过点 0(-3, -4),求角 的正 2.已知角α 终边经过点P 已知角 求角 余弦和正切值. 弦,余弦和正切值.
解: ∵x= -3, y=- 4, = =
∴ r = (3) + (4) = 5.
2 2
y
O
y 4 sin ∴ α = = = 4; r 5 5
cos α = x = 3 = 3 ; r 5 5
C.±3 ±
D. 5
b = 3 , ∴ cos α = x = 2 r 5 b + 16
解得 b = 3.
主页
1. 2. 1任意角的三角函数 (一) 任意角的三角函数 一
知识结构
三角函数的定义 任意角的 三角函数 三角函数的符号 定义域和值域 诱导(周角 公式一 诱导 周角)公式一 周角
主页
1. 2. 1任意角的三角函数 (一) 任意角的三角函数 一
α
O x 角 的终边在第一象限上
α
M
角的正弦,余弦,正切与 点的选取有关吗 点的选取有关吗? 角的正弦,余弦,正切与P点的选取有关吗?为 什么
答案
思考:角的终边如果在第二象限,第三象限,第四象限 思考:角的终边如果在第二象限,第三象限, 呢? 如果角的终边落在坐标轴上呢? 如果角的终边落在坐标轴上呢?

高一数学必修四课件第章二倍角的三角函数

高一数学必修四课件第章二倍角的三角函数

简化计算
利用二倍角公式可以将一些复杂的三 角函数表达式化简为更简单的形式， 从而方便计算。
求解方程
证明恒等式
二倍角公式在证明一些三角函数恒等 式时非常有用，可以通过将等式两边 转化为相同的二倍角形式来证明等式 成立。
在解三角函数方程时，有时可以利用 二倍角公式将方程转化为更容易求解 的形式。
02 二倍角的正弦、 余弦、正切函数
方法一
利用正切的定义tanα=sinα/cosα，将tan2α表示为 sin2α/cos2α，再利用正弦、余弦的二倍角公式化简得到 tan2α=(2tanα)/(1-tan²α)。
方法二
利用正切的加法公式，将tan2α表示为(tanα+tanα)/(1tanαtanα)，化简得到tan2α=(2tanα)/(1-tan²α)。
04 二倍角公式的应 用举例
在三角函数求值中的应用
利用二倍角公式将非特殊角的三角函 数转化为特殊角的三角函数进行求值 。
结合其他三角函数公式，如和差化积 、积化和差等，进行复杂表达式的求 值。
通过二倍角公式将高次三角函数降次 ，简化计算过程。
在解三角形中的应用
利用二倍角公式求解 三角形中的角度和边 长问题。
余弦函数的二倍角公式
公式表述
$cos 2alpha = cos^2 alpha sin^2 alpha$
推导过程
利用三角函数的和差化积公式， 将$cos 2alpha$表示为$cos
alpha$和$sin alpha$的平方差 形式。
应用举例
求$cos 2x$的值，可以通过已知 的$cos x$和$sin x$值代入公式
余弦二倍角公式的推导
方法一
利用三角函数的和差化积公式，将 cos2α表示为两个cosα的和差，通 过化简得到cos2α=cos²α-sin²α。

三角函数的概念(第一课时)课件-高一上学期数学人教A版(2019)必修第一册

三角函数的概念(第一课时)课件-高一上学期数学人教A版(2019)必修第一册
10
终边相同的角的三角函数值
如果两个角的终边相同，那么这两个角的同一三角函数值有何关系？
终边相同
终边与单位圆
交点坐标相同
角的同一三角
函数值相同
终边相同的角的同一三角函数值相等(公式一)
P(x,y)
公式一（弧度制）
公式一（角度制）
y
sin( k 2 ) sin
sin( k 360) sin
5
解 : 如图, 在直角坐标系中, 作AOB
,
3
1
3
易知AOB的终边OB与单位圆的交点坐标为B( ,
).
2
2
5
3 cos 5 1 , tan 5 3.
sin

,
3 2
3
3
2
7
1
3 1
7
3
7
3
sin


,
(
, )
cos

, tan

.
6
2
2
2
6
2
6
3
cos x
§5.2.1 三角函数的概念
情景引入
抽象为
问题：匀速圆周运动是生活中周期现象的代表，我们知道函数是刻画世界
变化规律的重要教学模型，那么匀速圆周运动应该用什么模型来刻画它？
任务：建立一个函数模型，来刻画P点的位置变化？
以原点为圆心，以单位长度1为半径的圆，称为单位圆.
如图，单位圆上的点P以A为起点做逆时针方向旋转，射线从起始位置OA按逆时针方向旋转到终止位
据初中所学过的三角函数的定义，有
y
P(a,b)
0
1
α

《高一数学三角函数课件》

《高一数学三角函数课件》
给出三角函数求值在实际应用中的例子， 如建筑物高度和测量角度。
介绍正弦函数的奇偶性、增 减性、单调性以及在三角恒 等式中的重要作用。
应用
阐述正弦函数在物理中描述 周期性运动的应用，如弹簧 振子和天体运动。
4. 余弦函数及其图像和特点
1
图像
展示余弦函数的典型波形图，解读
特点
2
其周期、振幅和相位角度。
介。
3
应用
应用
阐述正割函数在物理中描述 角度和比例关系的应用，如 光学和三角定理。
8. 余割函数及其图像和特点
1
图像
展示余割函数的典型图像，解读其
特点
2
周期和渐近线。
介绍余割函数的周期性、奇偶性、
增减性以及与正割函数的关系。
3
应用
阐述余割函数在物理中描述角度和 比例关系的应用，如电路分析和角 速度。
9. 角度制和弧度制的转换及应 用
2. 周期函数的概念及特点
1 周期性
2 图像特点
解释什么是周期函数，以及 周期函数的周期长度和性质。
讲解周期函数图像的周期性 重复、对称轴、峰值和谷值 等特点。
3 应用举例
引用实际例子，说明周期函数在日常生活中的应用场景。
3. 正弦函数及其图像和特点
图像
特点
展示正弦函数的典型波形图， 解读其周期、振幅和相位角 度。
图像
展示余切函数的典型图像， 解读其周期和渐近线。
特点
介绍余切函数的周期性、 奇偶性、增减性以及与正 切函数的关系。
应用
阐述余切函数在物理中描 述角度和瞬时变化率的应 用，如斜率和无穷大的概 念。
7. 正割函数及其图像和特点
图像
展示正割函数的典型图像， 解读其周期和渐近线。
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

2
2
tan 3 cot tan 3 cot
2
2
tan tan tan tan
tan tan tan2 tan
y
2
0 2
设0
2
tan 0
3
2
x 2
3
2
四、 cot
2
tan
cot tan
sin
12
3 2
cos
12
2
sin
12
cos
3
cos
12
sin
3
2
sin
12
3
2
sin
5
12
书P415、7(1、2、4）
2
一、
sin
2
cos
x
2
3
2
sin
cos
2
sin 3 cossin 3 cos
2
2
sin sin sin sin
sin sin sin 2 sin
y
2
0 2
设0
2
sin 0
3
2
二、 cos sin
和余弦ቤተ መጻሕፍቲ ባይዱ否求出两角和与
两角差的正弦呢？
sin(α+β)=
cos[
2
-(α+β)]
=cos[( )－β］
2
=cos( )cosβ+sin(
2
)sinβ
2
＝sinαcosβ+cosαsinβ
∴ sin(α+β)=sinαcosβ+cosαsinβ
两角和与差的正弦公式
1、两角和的正弦公式
sin( ) sin cos cos sin
（3）cos15 6 2 4
2、已知cos =
3 5
，
0，
2
，求
sin(
6
).
解：
cos
=
3 5
，
0，
2
sin
1 cos2
1
3 5
2
4 5
sin( ) sin cos cos sin
6
6
6
4 5
3 2
3 5
1 2
4 33. 10
3、证明：(1)sin( ) sin( sin2 cos2
2
cot 3 tan
2
cot 3
2
tan
cot cot cot cot
cot cot cot2 cot
1、已知cos( ) 1 ，求sin( 3 )的值.
4
2
2、已知tan(3 ) 3，求cos(3 )的值.
2
2
二 已知两个角的正弦
P2
0
P3 cos ,sin
P4 cos ,sin
P1
P1P3 P2P4
x
cos( ) cos cos sin sin
P4
3、两角差的余弦公式
用 代
cos( ) cos cos sin sin
y
2
0 2
设0
2
cos 0 cos 0
3
P2
P1(x1，y1) P2 (x2，y2 ) P1Q M1M2 x1 x2 P2Q N1N2 y1 y2
M1
M2
0
x
P1
N1
Q
P1P2 P1Q2 P2Q2
x1 x2 2 y1 y2 2
两角和与差的余弦公式
2、两角和的余弦公式 y
P1 1,0 P2 cos,sin
P3
)
1
cot 2
tan2
.
(2) cos 3 sin 2sin( )
6
左边
2
1 2
cos
3 2
sin
2 sin cos cos sin
6
6
2sin( )
6 右边.
4、求值(1)cos75 sin15 sin 75 cos15
(2)sin 3 cos
12
12
2
1 2
2、两角差的正弦公式
用 代
sin( ) sin cos cos sin
1、不查表求sin105 、sin75 与cos15 .
解：（1）sin105 sin（60 45 ）
= sin 60 cos 45 cos 60 sin 45
3 2 1 2 2 2 22
6 2 4
（2）sin 75 6 2 4
课题：§4.6 两角和与差的三角函数 （二）
江西省玉山一中 胡勇进
§4.6 两角和与差的三角函数 （二）
我们的目标
1. 掌握两角和与差的正弦公式
2. 结合余弦公式初步涉及“变角”和“拆 角”以及“合一变形”的方法
3. 正弦、余弦、正切、余切的诱导公式
两角和与差的余弦公式
1、两点间的距离公式
y
N2
x 2
3
c2os sin
2
2
cos 3 sin cos 3 sin
2
2
cos cos cos cos
cos cos cos2 cos
y
2
0 2
设0
2
cot 0
3
2
x 2
3
2
三、 tan cot tan cot