曲线的凹凸性与拐点

曲线的凹凸性与拐点在数学中，曲线的凹凸性以及拐点对于研究曲线的性质和变化具有重要的意义。

凹凸性可以帮助我们理解曲线的弯曲程度以及变化趋势，而拐点则是曲线上的一个特殊点，表示曲线在该处发生方向的变化。

本文将介绍曲线的凹凸性与拐点的概念，以及它们在数学和其他实际应用中的重要性。

一、凹凸性的定义与判断凹凸性是描述曲线在某一区间上的弯曲程度的性质。

我们有以下两个定义来判断曲线的凹凸性：1. 凹曲线：如果曲线上的任意两点连线的下方部分都在曲线上方，则称该曲线为凹曲线。

换句话说，如果对于曲线上的任意两点A和B，A和B连线的下方不与曲线相交，则该曲线为凹曲线。

2. 凸曲线：如果曲线上的任意两点连线的下方部分都在曲线下方，则称该曲线为凸曲线。

换句话说，如果对于曲线上的任意两点A和B，A和B连线的下方不与曲线相交，则该曲线为凸曲线。

凹凸性的判断可以通过曲线的二阶导数来进行。

如果曲线的二阶导数大于0，则曲线为凹曲线；如果二阶导数小于0，则曲线为凸曲线。

而当二阶导数恰好为0时，需要考虑其他方法。

二、拐点的定义与判断拐点是曲线上的一个特殊点，表示曲线在该点处方向发生改变。

我们有以下定义来判断曲线是否存在拐点：1. 拐点：如果曲线在某一点处既没有切线也没有二阶切线（即曲线在该点处没有明确的方向），则称该点为拐点。

判断曲线是否存在拐点可以通过曲线的三阶导数来进行。

如果曲线的三阶导数存在不连续的点，则该点即为拐点。

值得注意的是，如果曲线的三阶导数的符号在该点的左右两侧不同，也可以判断该点为拐点。

三、凹凸性与拐点的应用与意义凹凸性和拐点不仅仅在数学领域中有重要性，还被广泛应用于其他学科和实际问题中，如物理学、经济学等。

在物理学中，凹凸性可以帮助解释某一物体的形状和弯曲程度，例如在光学中，曲率半径越小的曲面会导致光线的弯曲程度越大。

因此，通过研究光线在曲面上的传播可以利用凹凸性来分析光的折射和反射现象。

在经济学中，凹凸性可以用来描述供需曲线的变化趋势。

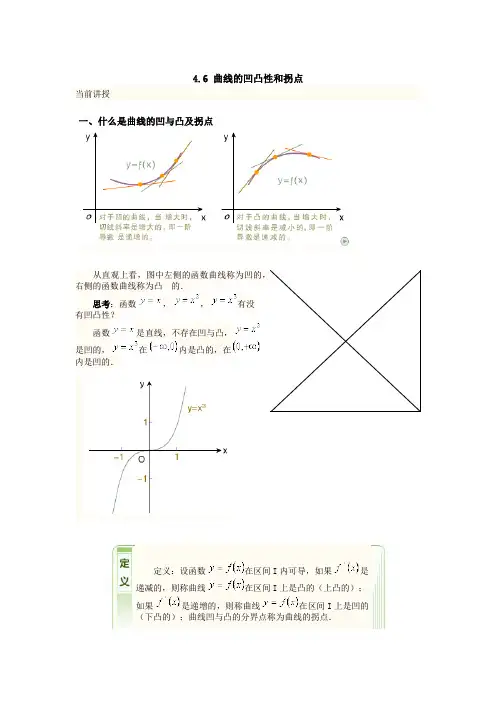
4.6 曲线的凹凸性和拐点当前讲授一、什么是曲线的凹与凸及拐点从直观上看，图中左侧的函数曲线称为凹的，右侧的函数曲线称为凸的．思考：函数，，有没有凹凸性？函数是直线，不存在凹与凸，是凹的，在内是凸的，在内是凹的．定义：设函数在区间I内可导，如果是递减的，则称曲线在区间I上是凸的（上凸的）；如果是递增的，则称曲线在区间I上是凹的（下凸的）；曲线凹与凸的分界点称为曲线的拐点．在下面这张图中．曲线在AB段是凸的，在BC段是凹的．凹与凸的分界点B就是拐点．二、曲线的凹凸性与二阶导数的关系定理一：若在内有，则曲线在上是凹的；若在内有，则曲线在上是凸的；两侧二阶导数异号的点是拐点．可简记为：曲线凹（开口向上）曲线凸（开口向下）定理二（拐点的必要条件）：若点是曲线的拐点，且处二阶导数存在，则必有．反之，二阶导数为零的点未必是拐点．例如函数，在内其二阶导数处处为零，但曲线无拐点．此外，二阶导数不存在的点也可能是拐点．例如的二阶导数，在内，曲线是凹的；在内，曲线是凸的，所以原点是拐点，但在处二阶导数不存在．三、求曲线凹凸区间及拐点的步骤拐点隐藏在那些二阶导数为0和二阶导数不存在的点中．判定曲线凹凸性及求拐点的步骤：（1）求定义域（如果题目指定了区间，则此步骤可省略）．（2）求二阶导数为零的点及不存在的点．（3）列表分析．以上述点划分定义域，在各子区间确定的符号，从而确定曲线的凹凸区间，进而确定拐点．注意：拐点是曲线上的点，应表示为的形式．典型例题例4.6.1判定曲线的凹凸性．提示>>解定义域：，，在内，，曲线在内是凹的．例4.6.2讨论曲线的凹凸性，并求出它的拐点．提示>>解定义域：令，得二阶导数为零的点为，．无二阶导数不存在的点．－0 －0 +不对应拐点对应拐点可见：曲线在区间上是凸的，在区间上是凹的．有一个拐点，此拐点的横坐标，纵坐标，即曲线的拐点为．例4.6.3已知的拐点为，且在处有极值．求a、b、c．提示>>解：，∵是函数的极值点，且函数在该点可导，∴必然是驻点，于是有，即 (1)，∵点为拐点，且函数在该点二阶可导，∴在处函数的二阶导数必然为零，于是有，即 (2)又即 (3)联立求解方程（1）（2）（3），即可解得：，，．。

掌握曲线的凹凸性和拐点的判定方法
在数学和物理学中，我们经常需要分析曲线的性质，如凹凸性
和拐点。

掌握这些判定方法可以帮助我们更好地理解曲线的行为和
特征。

本文将介绍一些常用的方法来判断曲线的凹凸性和拐点。

凹凸性的判定方法
一阶导数的方法
曲线的凹凸性与一阶导数的正负相关。

若曲线上任意一点处的
一阶导数大于零，则曲线在该点上是凸的；若一阶导数小于零，则
曲线在该点上是凹的。

二阶导数的方法
曲线的凹凸性也可以通过二阶导数来判断。

求曲线的二阶导数，然后观察二阶导数的正负性。

若二阶导数恒大于零，则曲线是凸的；若二阶导数恒小于零，则曲线是凹的。

切线的方法
通过画出曲线上某一点的切线，观察切线与曲线相交的情况可以判断凹凸性。

如果曲线上的切线位于曲线下方，那么曲线在该点是凹的；如果切线位于曲线上方，曲线在该点是凸的。

拐点的判定方法
拐点是曲线上的特殊点，曲线在该点上发生凹凸性的变化。

下面介绍一些常用的方法来判断拐点。

二阶导数的方法
寻找曲线上的拐点可以通过观察二阶导数的零点来判断。

如果二阶导数在某一点处为零并且两侧符号不同，那么该点就是曲线的拐点。

曲率的方法
曲线上某一点的曲率表示了曲线在该点上的弯曲程度。

拐点处的曲率会发生突变。

因此，通过计算曲线在不同点处的曲率，并观察曲率的变化情况，可以确定曲线上的拐点。

总结
通过使用一阶导数、二阶导数和曲率等方法，我们可以判断曲线的凹凸性和拐点。

这些方法在数学和物理学的分析中是常用的，能够帮助我们更全面地了解曲线的特性。

曲线的凹凸性与拐点为了进一步研究函数的特性并正确地作出函数的图形，需要研究曲线的弯曲方向.在几何上，曲线的弯曲方向是用曲线的“凹凸性”来描述的.一、 曲线的凹凸性 从图3-12（a ），（b ）可以观察到.定义1 如果在某区间内的连续且光滑曲线弧总是位于其任一点切线的上方，则称此曲线弧在该区间内是凹的；如果在某区间内的曲线弧总是位于其任一点切线的下方，则称此曲线弧在该区间内是凸的，相应的区间分别称为凹区间与凸区间.从图3-12还可以看到如下事实：对于凹的曲线弧，其切线的斜率()f x '随着x 的增大而增大，即()f x '单调增加；对于凸的曲线弧，其切线的斜率()f x '随着x 的增大而减少，即()f x '单调减少.而函数()f x '的单调性又可用它的导数，即()f x 的二阶导数()f x ''的符号来判定，故曲线()y f x =的凹凸性与()f x ''的符号有关.定理1 设函数()f x 在区间(,)a b 上具有二阶导数.（1）如果在区间(,)a b 上，有()f x ''>0，那么曲线在(,)a b 上是凹的； （2）如果在区间(,)a b 上，有()f x ''<0，那么曲线在(,)a b 上是凸的. 例1 判定曲线ln y x =的凹凸性. 解 函数的定义域为(0,)+∞，而 211,y y x x'''==- 因此曲线ln y x =在(0,)+∞内是凸的. 例2 讨论曲线3y x =的凹凸区间.解 函数的定义域为(,)-∞+∞， 23,6y x y x '''==显然，当0x >时，0y ''<；当0x <时，0y ''>.因此(,0)-∞为曲线的凸区间，(0,)+∞为曲线的凹区间.二、 曲线的拐点在例2 中，点(0,0)为凸的曲线弧与凹的曲线弧的连接点，对这种点有如下定义. 定义2 在连续曲线上，凹凸曲线弧的分界点，称为曲线的拐点. 下面来讨论曲线()y f x =拐点的求法.由于拐点是曲线凹凸弧的连接点，如果()f x ''存在且连续，则在拐点的左右近旁()f x ''必然异号，因此曲线拐点的横坐标0x ，是可能使()f x ''=0的点，从而可知求拐点的步骤为：（1） 求()f x ''；（2） 令()f x ''=0，解出方程()f x ''=0在某区间内的实根0x ；（3） 对每一个实根0x ，考察()f x ''在0x 的左右近旁的符号，若()f x ''在0x 的左右近旁的符号相反，则点00(,())x f x 是拐点，若()f x ''在0x 的左右近旁的符号相同，则点00(,())x f x 不是拐点.例3求曲线453151x x y -=的凹凸区间与拐点. 解 函数的定义域为(,)-∞+∞ 3434x x y -='，)1(444223-=-=''x x x x y 令 0y ''=，得 1,0==x x .由于0=x 的左右近旁y ''不改变符号，（0，0）不是拐点.当1<x 时，0<''y ；当 1>x 时，0>''y . 所以曲线在)1,(-∞内是凸的，在+∞,1(）内是凹的；（)152,1-为拐点. 注意：使()f x ''不存在而()f x 连续的点，也可能成为曲线的拐点. 例4 求曲线53y x =的拐点.解 定义域为(,)-∞+∞， 2353y x '=，1310,(0)9y x x -''=≠ 因为令0y ''=时，方程 131009x -=无解.而当0x <时，0y ''<；当0x >时，0y ''>， 即曲线在区间(,0)-∞内是凸的，在区间(0,)+∞内是凹的，又曲线在点0x =处是连续的，所以点（0，0）是曲线的拐点.三、 函数绘图 1、渐近线定义3 如果一动点沿某曲线变动，其横坐标或纵坐标趋于无穷远时，它与某一固定 直线的距离趋向与零，则称此直线为曲线的渐近线.例如直线 0,0x y x ya b a b -=+=为双曲线12222=-by a x 的渐近线.但并不是所有的曲线都有渐近线，下面只对两种情况的渐近线予以讨论.（1）水平渐近线如果当自变量x →∞时，函数()f x 以常量C 为极限，即lim ()x f x C →∞=，则称直线y C =为曲线()y f x =的水平渐近线.（2）铅直渐近线（或垂直渐近线）如果当自变量0x x →时，函数()f x 为无穷大量，即0lim ()x x f x →=∞，则称直线0x x =为曲线()y f x =的铅直渐近线.说明：对x →∞时，有时也可能仅当x →+∞或x →-∞；对0x x →，有时也可能仅当0x x +→或0x x -→.例5 求下列曲线的水平或垂直渐近线.（1）3223x y x x =+- （2）22x y -=.解 （1）因为323lim 23x x x x →-=∞+-， 321lim 23x x x x →=∞+- 所以直线 3,1x x =-=是两条铅直渐近线.（2） 因为220x x -=，所以直线0y =为其水平渐近线.2、函数图形的描绘利用导数描绘函数图形的一般步骤为：（1） 确定函数的定义域，考察函数的奇偶性、周期性； （2） 确定函数的单调区间、极值点、凹凸区间以及拐点； （3） 考察渐近线；（4） 作一些辅助点；（5） 由上面的讨论，画出函数的图形例6 作函数32()31fx xx =-+的图形.解 （1）函数定义域为(,)-∞+∞；（2）2()36f x x x '=-， 令()0f x '= 得 120,2x x ==；f ''”表示上升且为凸的，”表示上升且为凹的.（3（4）取辅助点（1,3)--、（3，1）；（6） 画图（如图3-13）例7作函数1)2(12---=x x y 的图形.解 定义域为),2()2,(+∞⋃-∞ 342)2()2()2)(1(2)2(--=-----='x xx x x x y 令0='y ，得0=x ； 4623)2()1(2)2()2(3)2(-+=-----=''x x x x x x y ， 令0=''y ，得1-=x ；列表：渐近线：因为∞=---+→]1)2(1[lim 22x x x ，所以2=x 是铅直渐近线；又因为1]1)2(1[lim 2-=---∞→x x x ，所以1-=y 是水平渐近线. 作辅助点：（)1,1-、)0,255(-、)45,0(-. 作图：（如图3-14）习题1、判定下列曲线的凹凸性： （1）)0(2≠++=a cbx ax y ； （2）x x y arctan =.2、求下列曲线的拐点及凹凸区间：（1）53523-+-=x x x y ； （2）321--=x y .3、求下列曲线的水平或垂直渐近线：（1）1232-+-=x x x y ； （2）x e y 1=；（3）)1ln(xey +=； （4）11+-=x e y x . 4、作函数的图形：（1）1612823++-=x x x y ； （2）2x e y -=； （3）3443x x y -=； （4）xxe y -=.。