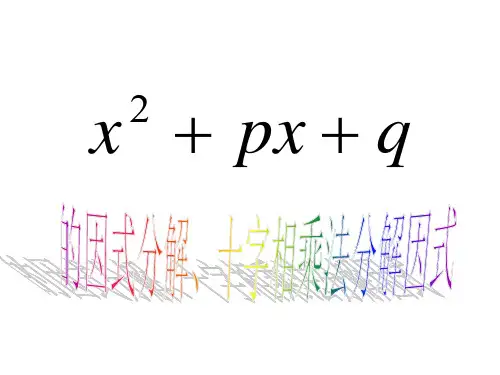当前位置：文档之家 › 初一数学《因式分解》ppt课件

初一数学《因式分解》ppt课件

  • 格式：ppt
  • 大小：425.50 KB
  • 文档页数：8

下载文档原格式

  / 8

合集下载

课件《因式分解》精美PPT课件_人教版2

课件《因式分解》精美PPT课件_人教版2
（2）S1=S2，相同的两2个长方形拼成的两个图形的面积相等，即都等于这两个长方形面积的和.
解：原式＝（a2+1）（a+1）（a-1）.
原式＝3x（2x+1）（2x-1）.
-2x（x+1）（x-1）
（3b+2a）（3b-2a）
3（x+2）（x-2）
解：原式＝（m-2）（n+1）（n-1）．
； .
6. （例 2）分解因式：
三级检测练
一级基础巩固练
14. 分解因式：
（1）x2-25=
（x+5）（x-5）
；
（2）4b2-a2=
（2b+a）（2b-a）
；
（3）9b2-4a2=
（3b+2a）（3b-2a）
.
15. 下列各式中，能用平方差公式分解因式的是
（D ）
A. 2a2-b2
B. y2+9
C. -x2-y2
D. x2-1
（2）2m（2m-3）+6m-1. （2b+a）（2b-a）
原式＝y（3x+1）（3x-1）.
2y（x+2）（x-2）
解：原式＝（m-2）（n+1）（n-1）．
（2）S1=S2，相同的两个长方形拼成的两个图形的面积相等（x+1）（x-1）
解：原式＝（4x2+1）（4x2-1）
3. 平方差公式：
整式乘法：（a+b）（a-b）= a2-b2
；
分解因式：a2-b2=
（a+b）（a-b）
.
4. （例 1）分解因式：
（1）x2-4=
（x+2）（x-2）

2.4《因式分解法》课件(共35张PPT)

2.4《因式分解法》课件(共35张PPT)
2、用适当方法解下列方程 ① -5x2-7x+6=0
② 2x2+7x-4=0
③ 4(t+2 3 )2=3
④ x2+2x-9999=0
（5） 3t(t+2)=2(t+2)
小结： 1、
ax2+c=0
====>
直接开平方法
ax2+bx=0 ====>
因式分解法
ax2+bx+c=0 ====>
因式分解法 公式法（配方法）
① x2-3x+1=0 ② 3x2-1=0
③ -3t2+t=0
④ x2-4x=2
⑤ 2x2－x=0
⑥ 5(m+2)2=8
⑦ 3y2-y-1=0 ⑧ 2x2+4x-1=0
⑨ (x-2)2=2(x-2)
适合运用直接开平方法
；
适合运用因式分解法
；
适合运用公式法
；
适合运用配方法
.
我的发现
➢一般地，当一元二次方程一次项系数为0时 （ax2+c=0），应选用直接开平方法；
例3.解下列方程 :
(1)x(x 2) x 2 0;
(2)5x2 2x 1 x2 2x 3 .
4
4
可以试用 多种方法解 本例中的两
个方程 .
分解因式法解一元二次方程的步骤是: 1.将方程右边等于0; 2. 将方程左边因式分解为A×B; 3. 根据“ab=0,则a=0或b=0”,转化为两个一元一次方程. 4. 分别解这两个一元一次方程，它们的根就是原方程的根.
➢若常数项为0（ ax2+bx=0），应选用因式分解法；
➢若一次项系数和常数项都不为0 (ax2+bx+c=0）， 先化为一般式，看一边的整式是否容易因式分解， 若容易，宜选用因式分解法，不然选用公式法；

课件《因式分解》PPT_完美课件_人教版2

课件《因式分解》PPT_完美课件_人教版2

所学的解题过程，我们应用了如下关系：
x(a−b)3+y(b−a)3=(a−b)3(x+y)
因式分解与整式乘法是互逆过程.
（1）8a3b2+12ab3c (6) m2－4=(m+2)(m－2)
14.3.1 提公因式法因式分解
理解公因式的概念，会根据“三定法”确定公因式。
(7) 2πR+ 2πr= 2π(R+r)
新的多项式中若 有小括号，要化
简
即是提公因式后剩下的另一个因式.
练一练
下面的因式分解正确吗？
➢ 3x2y−9xy2=3x(xy−3y2) 3xy (x−3y) ➢ 4x2y−6xy2+2xy=2xy(2x−3y) 2xy (2x−3y+1) ➢ x(a−b)3+y(b−a)3=(a−b)3(x+y) (a−b)3(x−y)
分解因式
例1: 找 3x 2 – 6 x3y 的公因式.
因式分解与整式乘法有何关系?
提公因式并确定另一个因式：要确定另一个因式，可用原多项式除以公因式，所得的商即是提公因式后剩下的另一个因式.
所以，公因式是3x2 .
所以，公因式是3x2 . 所以，公因式是3x2 . 所以，公因式是3x2 .
第十四章 整式的乘法
(5) (a－3)(a+3)=a2－9
定系数，再确定字母，最后确定公因式字母 【名师点拨】别忘记最后核实括号内的多项式是否还有公因式。
2）(x+2)(x-2)= 这种分解因式方法叫提公因式法。
6）a2+2ab+b2= 是pa+pb+pc除以p的商
2xy (2x−3y+1)
的指数；

因式分解ppt课件

因式分解ppt课件

方式.
完全平方式的条件：(1)多项式是二次三项式；(2)首末
两项是两个数(或式子)的平方且符号相同，中间项是这
两个数(或式子)的积的2 倍，符号可以是“＋”，也可以
是“－”.
感悟新知
知5－讲
2. 完全平方公式
两个数的平方和加上(或减去)这两个数
的积的2 倍，等于这两个数的和(或差)的平方.
即：a2±2ab＋b2＝(a±b)2 .
知4－讲
3. 运用平方差公式分解因式的步骤
一判：根据平方差公式的特点，判断是否为平方差，若负
平方项在前面，则利用加法的交换律把负平方项放在后面；
二定：确定公式中的a和b，除a和b是单独一个数或字母外，
其余不管是单项式还是多项式都必须用括号括起来，表示
一个整体；三套：套用平方差公式进行分解；四整理：将
(2)确定另一个因式，另一个因式即多项式除以公因式所
得的商；
(3)写成积的形式.
感悟新知
知3－讲
特别解读
1. 提公因式法实质上是逆用乘法的分配律.
2. 提公因式法就是把一个多项式分解成两个因式的积的形
式，其中的一个因式是各项的公因式，另一个因式是多
项式除以这个公因式所得的商.
感悟新知
知3－练
例 5 把下列多项式分解因式：
感悟新知
例 3 仔细阅读下面例题，解答问题：
知1－练
例题：已知把x2－4x＋m分解因式后有一个因式是x
＋3，求其另一个因式及m的值.
解：设另一个因式为x＋n，则x2－4x＋m＝(x＋3)(x
＋n)，即x2－4x＋m＝x2＋(n＋3)x＋3n.
＝－，
＋＝－，
所以
解得
＝－.

《因式分解》ppt全文课件

《因式分解》ppt全文课件

思路点拨：因式分解法解一元二次方程的步骤是： (1)化方程为一般形式； (2)将方程左边因式分解； (3)至少有一个因式为零，得到两个一元一次方程； (4)两个一元一次方程的解就是原方程的解． 但要具体情况具体分析．
解：(1)方程可变形为 y(y＋7)＝0， ∴y＋7＝0 或 y＝0.∴y1＝－7，y2＝0. (2)∵方程可变形为 t(2t－1)－3(2t－1)＝0， ∴(2t－1)(t－3)＝0. ∴2t－1＝0 或 t－3＝0.∴t1＝12，t2＝3.
∴(3x＋2)(15x＋10－3x)＝0.
∴3x＋2＝0 或 12x＋10＝0.∴x1＝－23，x2＝－56.
《因式分解》上课实用课件（PPT优秀 课件）
《因式分解》上课实用课件（PPT优秀 课件）
4．我们已经学习了一元二次方程的四种解法：直接开平方 法、配方法、公式法和因式分解法．请从以下一元二次方程中 任选一个，并选择你认为适当的方法解这个方程．
《因式分解》上课实用课件（PPT优秀 课件）
《因式分解》上课实用课件（PPT优秀 课件）
2．用因式分解法解下列方程： (1)(x－4)(x＋1)＝0； (2)(5x－1)(x＋1)＝(6x＋1)(x＋1)． 解：(1)(x－4)(x＋1)＝0，即 x－4＝0 或 x＋1＝0. ∴x1＝4，x2＝－1. (2)(5x－1)(x＋1)＝(6x＋1)(x＋1)， ∴(5x－1)(x＋1)－(6x＋1)(x＋1)＝0， (x＋1)(5x－1－6x－1)＝0. ∴(x＋1)(－x－2)＝0. 即 x＋1＝0 或－x－2＝0.∴x1＝－1，x2＝－2.
《因式分解》上课实用课件（PPT优秀 课件）
《因式分解》上课实用课件（PPT优秀 课件）
【跟踪训练】

因式分解的ppt课件

因式分解的ppt课件

包权
人书友圈7.三端同步
VIP专享文档下载特权自VIP生效起每月发放一次， 每次发放的特权有效期为1个月，发放数量由您购买 的VIP类型决定。
每月专享9次VIP专享文档下载特权， 自VIP生效起每月发放一次，持续有 效不清零。自动续费，前往我的账号 -我的设置随时取消。
服务特 权
共享文档下载特权
VIP用户有效期内可使用共享文档下载特权下载任意下载券标价的文档（不含付费文档和VIP专享文档），每下载一篇共享文
初步应用提公因式法
例1 把 8a3b2+12ab3c 分解因式．
解： 8a3b2+12ab3c =4ab2 2a2+4ab2 3bc =4ab（2 2a2+3bc）.
例2 把 2（ a b+c）-（3 b+c）分解因式．
解： 2（ a b+c）-（3 b+c） =（b+c）（2a-3）.
提公因式法
（5） x2 1 x( x 1 ) x
（6） 18a3bc 3a2b6ac
不是 不是 不是
说明
• 本课是在学生学习了整式乘法的基础上，研究对整 式的一种变形即因式分解，是把一个多项式转化成 几个整式相乘的形式，它与整式乘法是互逆变形的 关系．
什么叫因式分解？ 把一个多项式写随时随地彰显尊贵身份。
专属客服
VIP专属客服，第一时间解决你的问题。专属客服QQ：800049878
路漫部权益：1.海量精选书免费读2.热门好书抢先看3.独家精品资源4.VIP专属身份标识5.全站去广告6.名
提公因式法
一般地，如果多项式的各项有公因式，可以把这个 公因式提取出来，将多项式写成公因式与另一个因式的 乘积的形式．这种分解因式的方法叫做提公因式法．

因式分解ppt(共22张PPT)

因式分解ppt(共22张PPT)
3．（随堂练习p3１、２）
规律总结
• 对多项式分解因式与整式乘法是方向相反的两种恒等变 形.
• 整式的乘法运算是把几个整式的积变为多项式的形式，
特征是向着积化和差的形式发展；
• 多项式的分解因式是把一个多项式化为几个整式乘积的
形式，特征是向着和差化积的形式发展.
• 因式分解要注意以下几点: 1.分解的对象必须是多项式.
• 把一个多项式化成几个整式的积的形式,这 种变形叫做因式分解。
• 因式分解也可称为分解因式。
因分解的结果要以积的形式表示
2.每个因式必须是整式，且每个因式的次数 都要低于原多项式的次数。
3.必须分解到每个多项式不能分解为止（具 体由所在的数集决定）。
想一想: 因式分解与整式乘法有什么联系?
2.分解的结果一定是几个整式的乘积的形式.
2：计算
(1) 8728713 (2) 1012992
=87（87+13） =8700
=(101+99)(101-99) =200×2 =400
3.若 x101,y99则 x22xyy2_ 4_
动脑筋
n2+n是奇数还是偶数？
2517－532能被120整除吗? 若n是整数,证明 (2n+1)2-(2n-1)2是8的倍数.
多项式的因式分解与整式乘法是方向相反的恒等式.
整式乘法
3x(x-1)= _____
(3).(5a-1) =25a -10a+1 解: ab-ac=a(b-c)
a(a+1)(a-1) a3-a=a(a+1)(a-1)
2
2
整式乘法
答: 由a(a+1)(a-1)得到a3-a的变形是整式乘法，由a3-a得到a(a+1)(a-1)的变形是把一个多项式化成几个整式的积的形式.

因式分解_ppt1

因式分解_ppt1

x
3
x -7
x -3
x5
因式分解_ppt1
计算：(x+2)(3x+5) =3x2+11x+10 反过来：3x2+11x+10 =(x+2)(3x+5) 我们可以发现，二次项3x2分解成 x、3x 的积； 常数项10分解成 2、5 的积；
x
2
x ·5＋2 ·3x = 11x
3x
5
这个例子启发我们，如何把二次三项式
ax2+bx+c进行分解
因式分解_ppt1
因式分解_ppt1
例2、把下列各式分解因式：
（1）2x 2-7x+3
（2）6x 2-7x-5
（3）5x 2+6xy-8y2 （4）ab2+4abc+3ac 2
解：（1）原式=（x-3)(2x-1）
x
-3
2x -1
（2）原式=（2x+1)(3x-5）
2x 1 3x -5
因式分解_ppt1
x2 px q
因式分解_ppt1
1、(x+3)(x-4) =x2-x-12 2、(a-6)(a-5)=a2-11a+30 3、(y+1)(y-3) =y2-2y-3
(x a)(x b) x2 (a b)x ab
能分解x 2 5x 6吗？
(x a)(x b) x2 (a b)x ab
x2 x2 5x 6 (2) a2 2a 3 (3) x2 2x 8 (4) (x y)2 3(x y) 2
x 2 px q 分解方法
(1)找出a，b使a+b=p且ab=q (先分解q再考虑p)
(2)把q分解成两个整数的积的符号规律： q＞0则a，b同号， 若p＞0，a，b同正，若p＜0，a，b同负； q＜0则a，b异号， 若p＞0，a，b中正数绝对值大， 若p＜0，a，b中负数的绝对值大。

2-4《因式分解法》课件(共35张PPT)

2-4《因式分解法》课件(共35张PPT)
（1）提取公因式法: am+bm+cm=m(a+b+c).
（2）公式法:
a2-b2=(a+b)(a-b), a2±2ab+b2=(a±b)2.
（3）十字相乘法:
1 a
x2+(a+b)x+ab= (x+a)(x+b). 1 b
实际问题
根据物理学规律，如果把一 个物体从地面 10 m/s 的速度竖 直上抛，那么经过 x s 物体离地 面的高度（单位：m）为
3. 分别解两个一元一次方程，它们的根就 是原方程的根.
AB = 0
A=0或B=0
（ A、B 表示两个因式）
用因式分解法解一元二次方程的步骤
1. 方程右边化为_零_____。
2. 将方程左边分解成两个__一__次___因__式__的乘积。 3. 至少_有___一__个__因式为零，得到两个一元一次
⑴ 5x2-3 2 x=0 （运用因式分解法）
⑵ 3x2-2=0
（运用直接开平方法）
⑶ x2-4x=6
（运用配方法）
⑷ 2x2-x-3=0
（运用公式法）
⑸ 2x2+7x-7=0 （运用公式法）
② 公式法虽然是万能的，对任何一元二次方程都适用， 但不一定是最简单的，因此在解方程时我们首先考虑能 否应用“直接开平方法”、“因式分解法”等简单方法， 若不行，再考虑公式法（适当也可考虑配方法）
① x2-3x+1=0 ② 3x2-1=0
③ -3t2+t=0
④ x2-4x=2
⑤ 2x2－x=0
⑥ 5(m+2)2=8
⑦ 3y2-y-1=0 ⑧ 2x2+4x-1=0

《因式分解》PPT教学课件

《因式分解》PPT教学课件
2
m+n=1+ 3= 5.
22
课堂小结
因式分解
定义
把一个多项式化为几个整式的乘 积的形式,像这样的式子变形叫做 把这个多项式因式分解，也叫做 把这个多项式分解因式.其中，每 个整式叫做这个多项式的因式
随堂练习
1. 下列各式中从左到右的变形属于分解因式的是（ C ） A. a(a+b-1)=a2+ab-a B. a2-a-2=a(a-1)-2 C. -4a2+9b2=(-2a+3b)(2a+3b) D.2x +1=x(2+ 1 )
x
随堂练习
2.把x2+3x+c分解因式得x2+3x+c=(x+1)·(x+2)，则c的值 为（ A ）
历史课件： . /kejian/lishi/
c
b
a
ห้องสมุดไป่ตู้c n
d
方法一： （a+b+c）（n+d）
方法二： an+bn+cn+ad+bd+cd
（a+b+c）（n+d） =an+bn+cn+ad+bd+cd
课程讲授
1 因式分解的定义
问题1：
完成下列题目： x(x-2)=__x_2_-_2_x_ (x+y)(x-y)=__x_2-_y_2__ (x+1)2=_x_2_+_2_x_+_1_
第四章 因式分解
4.1 因式分解
新知导入
课程讲授
随堂练习
-.
课堂小结
知识要点
因式分解的定义即相关概念

精选 《因式分解》完整版教学课件PPT

精选 《因式分解》完整版教学课件PPT

也可以是多项式.
步骤
确定公因式,可按系数大(最大公约数),字母同 (各项相同的字母),指数低(相同字母的指数取 次数最低的)的规律来取；
将各项的公因式提出来,并确定另一个因式；用
式子表示: ma mb mc m(a b c) .
教材原题: [八上P115 练习第 1 题]把下列各式分解因式: (1) ax ay a(x y) . (2) 3mx 6my 3m(x 2y) .
第 4 课时 因式分解
考点 1:因式分解的概念
概念 关系
把一个 多项式 化成几个整式的 积 的形
式.这样的式子变形叫做这个多项式的因式分 解,也叫把这个多项式分解因式. 因式分解与整式乘法都是多项式的恒等变形,它 们互为逆运算.
教材原题: 下列各式是分解因式的是( C )
A. x2 3x 4 x(x 3) 4 B. 2(x y) 2x 2y C.1 4x 4x2 (1 2x)2 D. x2 y xy x(xy y)
.
点悟:有的因式分解不能一步到位,要分解到不能再
分解为止,有时还必需分解后再化简,或先化简后再 分解.
*考点 5:在实数范围内的因式分解
教材原题:
[八上P120 习题 14.3 第 11 题]在实数范围内分解因式:
(1) x2 2 ( x 2)( x 2) .
(2) 5x2 3 ( 5x 3)( 5x 3) .
2 4 1 9 32 6 8 1 49 72 1416 1 225 152 … 你能得出了什么结论?你能证明这个结论吗?
解:结论: (2n1 2) 2n1 1 (2n1 1)2 证明: (2n1 2) 2n1 1
(2n1 )2 2 2n1 1 (2n1 1)2 .

因式分解法-PPT课件

因式分解法-PPT课件

★ 选择适当的方法解一元二次方程
例2 用适当的方法解下列方程： （1）2（x-1）2-18 ＝ 0 ；
分析：出现了（x-1）2，并且一次项为0，考虑用直接开平方法. 解：整理，得（x-1）2＝ 9. 开平方，得x-1 ＝ ±3， 即x-1 ＝ 3 或x-1 ＝ -3， ∴ x1＝4，x2＝-2.
（2）x2+4x-1 ＝ 0 ；
(x + m) （x + n）＝0
Hale Waihona Puke 解法选择基本思路1.一般地，当一元二次方程一次项系数为0时（ax2+c=0）， 应选用直接开平方法； 2.若常数项为0（ ax2+bx=0），应选用因式分解法； 3.若一次项系数和常数项都不为0 (ax2+bx+c=0），先化为一 般式，看一边的整式是否容易因式分解，若容易，宜选用因 式分解法，不然选用公式法； 4.当二次项系数是1，且一次项系数是偶数时，用配方法也较 简单.
因式分解
x(x-7) =0 ②
两个因式乘积为 0，说明什么？
如果a · b = 0， 那么 a = 0或 b =
0.
x =0 或 x-7=0
降次，化为两个一次方程
x1 0, x2 7
（解两个一次方程，得出原方程的根） 这种解法是不是很简单？
例1 用因式分解法解下列方程
解：化为一般式为 x2－2x+1 = 0.
解：2(x－3)2＝(x＋3)(x－ 3)， (x－3)[2(x－3)－(x＋3)]＝0. 解得x1＝3，x2＝9. (3)5x(2x－3)＝10x－15.
解为（x+a）（x-a）＝ 0，则x+a ＝ 0 或x-a ＝ 0，即x1 ＝ -a， x2 ＝ a. （3）形如x2 ±2ax+ a2 ＝ 0 的一元二次方程，将左边用完全平方公式因式 分解为（x± a ）2＝ 0，则① x+a ＝ 0，即x1 ＝ x2 ＝ -a. ② x-a ＝ 0，即 x1 ＝ x2 ＝ a. （4）形如x2 +（a+b）x+ab ＝ 0 的一元二次方程，将其左边因式分解， 则 方程化为（x+a）（x+b）＝ 0，所以x+a ＝ 0 或x+b ＝ 0，即x1 ＝ -a， x2 ＝ -b.

初中数学教学课件因式分解共31页

初中数学教学课件因式分解共31页
25、学习是劳动，是充满思想的劳动。——乌申斯基
谢谢！
Байду номын сангаас 21、要知道对好事的称颂过于夸大，也会招来人们的反感轻蔑和嫉妒。——培根 22、业精于勤，荒于嬉；行成于思，毁于随。——韩愈
23、一切节省，归根到底都归结为时间的节省。——马克思 24、意志命运往往背道而驰，决心到最后会全部推倒。——莎士比亚
初中数学教学课件因式分解
11、获得的成功越大，就越令人高兴 。野心 是使人 勤奋的 原因， 节制使 人枯萎 。 12、不问收获，只问耕耘。如同种树 ，先有 根茎， 再有枝 叶，尔 后花实 ，好好 劳动， 不要想 太多， 那样只 会使人 胆孝懒 惰，因 为不实 践，甚 至不接 触社会 ，难道 你是野 人。(名 言网) 13、不怕，不悔(虽然只有四个字，但 常看常 新。 14、我在心里默默地为每一个人祝福 。我爱 自己， 我用清 洁与节 制来珍 惜我的 身体， 我用智 慧和知 识充实 我的头 脑。 15、这世上的一切都借希望而完成。 农夫不 会播下 一粒玉 米，如 果他不 曾希望 它长成 种籽； 单身汉 不会娶 妻，如 果他不 曾希望 有小孩 ；商人 或手艺 人不会 工作， 如果他 不曾希 望因此 而有收 益。-- 马钉路 德。
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

课堂总结： 想一想：下列式子从左边到右边是因式分解吗， 为什么？ A：（x +2）（x–2）= x2–4 B：x4－5x6y = x2（x2－5x4y）
C：x2－4＋3x = （x +2）（x–2）＋3x再见！来自例2把下列各式分解因式
(1)4a2+4ab+b2; (2)-24pqr+9p2q2+16r2; (3)4x2n+20xnyn+25y2n; 例3把下列各式分解因式 (1)16a2b-16a3-4ab2;
(2)(x2+1)2-4x(x2+1)+4x2
1． 判断下列因式分解是否正确，并简要说明理由：
§14.4 因式分解(3)
复习旧知,引入新课
把乘法公式 (a+b)2=a2+2ab+b2 (a-b)2=a2-2ab+b2 反过来,得到 2
a +2ab+b2=(a+b)2
a2-2ab+b2=(a-b)2
像a2+2ab+b2 或a2-2ab+b2这样的式子叫做完全平方式 上面方框内的两个公式就是完全平方公式. 运用完全平方式可以把完全平方式分解因式.
x2-4x+4,9m2+3mn+n2是不是完全平方式,你是 怎样识别的? 方法:先找到两个平方项,确定a,b,再看另一项 是不是2ab或-2ab. 例1 判别下列三项式是不是完全平方式;如果是, 请将该式分解因式. (1) x2+x+
1 ; 4
(2)9q2+p2-6pq; (3)m2+2mn+4n2
（1） 4a2－4a＋1＝4a（a－1）＋1
（2） x2－4y2＝（x＋4y）（x－4y） 2． 把下列各式分解因式： （1）a2＋a（2）4ab－2a2b（3）9m2－n2 （4）2am2－8a （5）2a2＋4ab＋2b2
3．
3 、丁丁和冬冬分别用橡皮泥做了一个长方体和圆 柱体，放在一起，恰好一样高。丁丁和冬冬想知道哪 一个体积较大，但身边又没有尺子，只找到一根短绳， 他们量得长方体底面的常正好是3个绳长，宽是2个绳 长，圆柱体的底面周长是10个绳长。你知道哪一个体 积较大吗？大多少？（提示：可设绳长为 a 厘米，长 方体和圆柱体的高均为 h 厘米）如果给你一架天平， 你有办法知道哪一个体积较大吗？