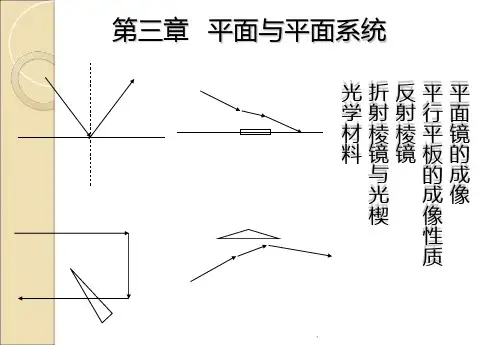
第3章 光学性质

第三章矿物的双反射及均质非均质性第一节矿物的双反射一、矿物双反射(反射多色性)的概念矿物的双反射(反射多色性)是在单偏光下看到的一种光学现象。

当转动台物改变物的方位时，有一些矿物的切面可观察到亮度(反射率)的变化，此即为矿物的“双反射(Bireflectance，Bireflection)”。

若转动物台观察到矿物反射色有变化时即为该矿物的“反射多色性(Reflection Pleochroism)”。

事实上，若采用现代化精密仪器测量任何等轴晶系以外的矿物，除均质切面以外的任何切面在转动物台改变矿物方位时其反射率都不相同，其反射色的颜色指数(视觉反射率R vis、主波长λd、纯度P e和色度坐标值x、y)也都会有所差异。

但是以观察者的视觉在矿相显微镜下却只能看到一部分矿物显示双反射和反射多色性。

往往是无色类和微弱颜色类矿物只观察到双反射(亮度变化明显、颜色变化不明显)，显著颜色类矿物主要观察到反射多色性(颜色变化明显、亮度变化较不明显)。

这是由于观察者视党灵敏度不够高而造成的。

人们可以利用矿物的双反射、反射多色性的差异在矿相显微镜下鉴定和鉴别金属矿物（表3－1）。

二、双反射(反射多色性)的形成机理关于双反射的形成机理，一般认为非均质矿物双反射的显著程度取决于矿物的相对双反射率(ΔR＇)，而与矿物的绝对双反射率(ΔR )没有太大的关系(表3—2)。

ΔR＝R 1- R2 ，ΔR＇＝ΔR/(R 1+ R2)/2式中R 1和 R2分别为矿物最大（最高）和最小（最低）的主反射率。

表3－2 矿物双反射与相对双反射率、绝对双反射率的关系示意表从表3－2可看出，虽然红砷镍矿的绝对双反射率 6.3％大于方解石的绝对双反射率(2.0%)，但红砷镍矿的双反射显著程度远低于方解石，这是由于红砷镍矿的相对双反射率(11.4％)明显地小于方解石的相对双反射率(40.8％)造成的。

十分明显，矿物相对双反射率包含了矿物亮度［平均反射率1／2(R 1+ R2)］因素在内。

高二物理第三章光学知识点光学作为物理学中的重要分支，研究的是光的本质、传播规律以及与物质相互作用的现象。

在高中物理课程中，光学是一个重要的章节，涉及到很多基本概念和原理。

本文将从几个主要方面介绍高二物理第三章光学的知识点。

一、光的传播与光的直线传播光是一种电磁波，具有特定的传播性质。

它以极高的速度传播，在真空中的速度约为3.0×10^8m/s，光在介质中传播时会发生折射现象。

当光在均匀介质中传播时，其传播路径呈直线，因此称为光的直线传播。

二、光的反射与光的折射光在与界面相遇时，会发生反射和折射。

光的反射是指光线从一介质射向另一介质时，遇到界面而改变传播方向的现象。

光的折射是指当光从一种介质射向另一种介质时，由于介质的折射率不同，光线改变传播方向的现象。

三、光的色散与光的衍射光的色散是指白光经过光的折射、反射、散射等现象时，由于不同波长的光在介质中的传播速度不同，使白光中的各种颜色分离出来的现象。

光的衍射是指光通过狭缝或障碍物后，在背后形成明暗条纹的现象。

四、光的成像与光的光路追迹法光的成像是指光通过透镜或反射镜后，在焦点处形成清晰的像的现象。

光的光路追迹法是一种基于光的传播规律，通过构建光线追迹图来解决光学成像问题的方法。

五、光学仪器与光学现象的应用光学仪器是利用光的传播、反射、折射等性质制作的具有特定功能的仪器。

常见的光学仪器包括显微镜、望远镜、光栅等。

光学现象的应用广泛，如光纤通信、激光技术、光学传感器等。

六、光的本质与光的量子性光的本质是物质与电磁场相互作用而产生的结果，既具有波动性，又具有粒子性。

根据光的量子性，光的能量是由量子的光子所携带的，光的强度与光子数目成正比。

总结起来，高二物理第三章光学主要涉及了光的传播、反射、折射、色散、衍射、成像、光学仪器、光学现象的应用以及光的本质和量子性等知识点。

通过学习这些知识，可以更深入地理解光的特性和行为，掌握光学原理，并能够将其应用于实际问题的解决中。

第二节光学性质一、反射与光泽纤维光泽的形成实际上是正反射光、表面散射反射光、来自内部的散射反射光的共同贡献，而透过光则决定于纤维的透明程度。

反射光量大，光泽好影响因素：1.纤维纵向形态：纤维表面是否平滑，如细毛的鳞片稠密，贴紧程度差，光泽差；粗毛鳞片紧贴毛干，光泽好。

2.截面形态（圆形、三角形）：如三角形截面有些内部反射光会在纤维截面的局部棱边上发生全反射，有“闪光”效果；圆形截面的纤维光线在任一界面上的入射角都和光线进入纤维后的折射角相等，在任何条件下都不能形成全反射，因此，这类纤维的透光性好，外观较明亮。

Y 形比三角形光泽更强。

3.纤维层状结构：几次反射、折射，表面反光量增加，光泽较强且柔和均匀，有层次，不耀眼。

二、折射与双折射双折射：进入纤维的光线分解成两条折射光，一条为寻常光线，也叫O光，其振动面与光轴垂直，折射率以n⊥表示；另一条光为非寻常光，不遵守折射定律，又叫e光，其振动面与光轴平行，折射率以n∥表示，光线顺光轴方向射入时不发生双折射，在非光轴方向n⊥和 n∥不同，光在内部进行的速度vo 和ve不同，折射率与光速成反比，大多数纺织纤维是正晶体，n⊥大于n∥不或vo 大于ve由于存在两个折射率，用n⊥-n∥表示双折射率。

双折射率的大小，与分子的取向度和分子本身的不对称程度有关，纤维中大分子与纤维轴平行排列时，双折射率最大，大分子紊乱排列时，双折射率为零。

一般用双折射率的大小来反映和比较同一种化学纤维各批间的定向度高低。

三、耐光性老化：变色、变硬、变脆、发粘、光泽差、强度差、破裂等。

太阳光通过宇宙空间和地球表面的大气层时，长波损失少，短波损失多，到达地球表面的紫外线数量少，其波长一般大于290nm。

短于290 nm的紫外线被高空的臭氧所吸收，波长越短，能量越大，光敏性：纤维分子不同，对紫外线的吸收有选择性，分子结构中含有C-C;C-H;C-N;C-O;C-CI 等键，一般不吸收波长大于290nm，故照射到地球表面的紫外线应该对这些纤维无影响，但实际上有裂解发生，主要是因为纤维中含有其他物质或杂质引起的氧化反应的结果，形成羟基，羟基能吸收280~320 nm的紫外线，所吸收的紫外线能量传给整个分子链去破坏那些不直接吸收紫外线的弱键。

光学计算问题交流讨论CASTEP中的光学计算是以电子结构计算为基础的，因为传统DFT在能带计算方面的问题，所以光学计算的准确性受到很大影响，但还是可以得到一些有用信息的。

而且对于一些strong Coulomb correlation的问题也可以通过LDA+U，LDA+SIC等等进行修正。

因此此方面也会得到更多发展，应用。

我抛砖引玉先提出一个问题，希望高手解答，大家讨论。

对于光学各向异性的晶体，我们要考虑方向性，CASTEP中提供了两个选项，分别是polarized和unpolarized，可以提供各向异性的考虑。

分别解释如下：Polarized - optical properties are calculated for plane polarized with the specified polarization direction;Unpolarized - optical properties are averaged over polarization directions perpendicular to the specified incident direction.但是这两种情况究竟分别适用与研究什么类型材料呢？下面以wur结构为例，此种提法：the electric field parallel （E平行c）和perpendicular （E垂直c）to the crystallographic c axis，分别对应于CASTEP中的哪个选项呢？还有一种提法是分成两个分量：two components, the in-plane component is the average over the x and y directions and the z component which is perpendicular to x-y plane. 这样z分量和x-y plane分量分别可以和CASTEP中的哪种情况对应呢？polarization vectors perpendicular (E垂直c)and parallel（E平行c）to the crystallographic c axis偏振矢量（or 极化矢量）分别垂直和平行c轴两种情况，这两种情况如果通过MS中对polarized和unpolaried的说明，其实都可以实现的，不知道具体有什么区别？选择两个选项的具体原则该是什么呢？大家多多讨论在回答上面问题的之前，我绝对有必要了解一下CASTEP计算光学性质的主要原理，CASTEP计算的光学性质主要电子能带结构中最基本的跃迁方式，其他的考虑不多，如声子（晶格振动吸收），激子，自由电子气光学响应等，在CASTEP里面也有这个说明了，比如：Limitations of the methodLocal field effectsThe level of approximation used here does not take any local field effects into account. These arise from the fact that the electric field experienced at a particular site in the system is screened by the polarizability of the system itself. So, the local field is different from the applied external field (that is, the photon electric field). This can have a significant effect on the spectra calculated (see the example of bulk silicon calculation below) but it is prohibitively expensive to calculate for general systems at present.Quasiparticles and the DFT bandgapIn order to calculate any spectral properties it is necessary to identify the Kohn-Sham eigenvalues with quasiparticle energies. Although there is no formal connection between the two, the similarities between the Schrödinger-like equation for the quasiparticles and the Kohn-Sham equations allowthe two to be identified. For semiconductors, it has been shown computationally (by comparing GW and DFT band structures) that most of the difference between Kohn-Sham eigenvalues and the true excitation energies can be accounted for by arigid shift of the conduction band upward with respect to the valence band . This is attributed to a discontinuity in the exchange-correlation potential as the system goes from (N)-electrons to (N+1)-electrons during the excitation process. There can, in some systems, be considerable dispersion of this shift across the Brillouin zone, and the scissor operator used here will be insufficient.Excitonic effectsIn connection with the absence of local field effects, excitonic effects are not treated in the present formalism. This will be of particular importance for ionic crystals (for example NaCl) where such effects are well known.Other limitations∙The nonlocal nature of the GGA exchange-correlation functionals is not taken into account when evaluating the matrix elements but it is expected that thiswill have a small effect on the calculated spectra.∙Phonons and their optical effects have been neglected.∙Finally, there is an intrinsic error in the matrix elements for optical transition due to the fact that pseudowavefunctions have been used (that is they deviatefrom the true wavefunctions in the core region). However, the selection ruleswill not be changed when going from pseudo- to all-electron wavefunctions ∙比如第一条所说的局域场效应，我们在计算光学跃迁的时候，外界跃迁激发电场在材料内部认为是没有衰减的，实际上由于内场的作用，一部分电场会被Screen了，但我们没有考虑。