沿程阻力系数表
- 格式:docx
- 大小:14.45 KB
- 文档页数:3


阻力:
妨碍物体运动的作用力,称“阻力”。
在一段平直的铁路上行驶的火车,受到机车的牵引力,同时受到空气和铁轨对它的阻力。
牵引力和阻力的方向相反,牵引力使火车速度增大,而阻力使火车的速度减小。
如果牵引力和阻力彼此平衡,它们对火车的作用就互相抵消,火车就保持匀速直线运动。
物体在液体中运动时,运动物体受到流体的作用力,使其速度减小,这种作用力亦是阻力。
沿程阻力系数表:
沿程阻力(Frictional Drag):流体流经一定管径的直管时,由于流体内摩擦力而产生的阻力,阻力的大小与路程长度成正比。
简介:
沿程阻力(直管阻力)损失的计算式中λ——摩擦系数,与雷诺数Re和管壁粗糙度ε有关,可实验测定,也可计算得出。
沿程阻力系数的确定方法:
对于层流流动,可以严格地从理论推导出来。
对于紊流流动,工程上通过以下两种途径确定:一种是以紊流的半经验理论为基础,结合实验结果,整理成阻力系数的半经验公式;另一种是直接根据实验结果,综合成阻力系数的经验公式。
前者具有更为普遍的意义。

管路沿程阻力计算1.摩擦阻力:在流体流动中,由于流体与管道壁之间的摩擦力,使得流体流动速度逐渐减小,产生摩擦阻力。
根据代表性的达西-魏泽巴赫公式,可以计算流体在管道中的摩擦阻力。
ΔP=λ(L/D)(ρV^2/2)其中,ΔP为单位管长上的摩擦阻力损失,λ为摩擦系数,L为管道长度,D为管道直径,ρ为流体密度,V为流速。
2.沿程局部阻力:在管道流动中,由于管道内部存在一些特殊设计或结构,导致流体流动时发生局部阻力。
根据达西-魏泽巴赫公式,可以计算管道局部阻力。
ΔP=K(ρV^2/2)其中,ΔP为单位管长上的沿程局部阻力损失,K为局部阻力系数,ρ为流体密度,V为流速。
3.管道弯曲阻力:在管道中,当流体流过弯曲部分时,会受到弯曲的影响,产生较大的阻力。
根据经验公式,可以计算管道弯曲阻力。
ΔP=K(ρV^2/2)其中,ΔP为单位管长上的弯曲阻力损失,K为弯曲阻力系数,ρ为流体密度,V为流速。
这些阻力形式在实际管道中经常同时存在,因此需要综合考虑计算总阻力。
通常采用经验公式、实验数据或数值模拟等方法进行计算。
在实际工程中,一般可以通过试验或计算得到相应的阻力系数,并且根据阻力计算公式,结合流体参数,来计算管路沿程阻力。
在实际应用中,管路沿程阻力的计算是非常重要的,它影响到管道系统的工作效率和输送能力。
为了降低阻力损失,有效节约能源,可以采取以下措施:优化管道布局,减少管道弯曲和局部阻力;选择合适的管道材料和直径,减小摩擦阻力;采用流体增压、注入润滑剂等方法来减小摩擦阻力。
总之,管路沿程阻力的计算是管道工程中的一个重要环节,通过合理地计算和设计,可以提高管道系统的效率和安全性,降低能源消耗。

管道的沿程阻力系数一、引言管道的沿程阻力系数是描述流体在管道中传输过程中阻力大小的一个重要参数。
准确求解管道的沿程阻力系数对于尺寸设计和流体运行状态的分析具有重要意义。
本文将从理论和实践两个角度,全面深入地探讨管道的沿程阻力系数的计算方法和影响因素。
二、沿程阻力系数的定义与计算方法2.1 定义沿程阻力系数,通常用符号λ表示,是指在单位长度内,管道内流体流动时所受到的摩擦阻力与单位长度内动压力头之比。
2.2 计算方法根据经验公式和实验数据,常用的计算方法包括Darcy-Weisbach公式、Colebrook-White公式和离散元法等。
2.2.1 Darcy-Weisbach公式Darcy-Weisbach公式是根据实验数据拟合出来的经验公式,可用于计算非常规流体或复杂流动情况下的沿程阻力系数。
公式形式如下:f=2λD⋅v22g其中,f为Darcy摩阻系数,λ为沿程阻力系数,D为管道直径,v为流速,g为重力加速度。
2.2.2 Colebrook-White公式Colebrook-White公式是一种较为常用的计算沿程阻力系数的方法,适用于流速较高的情况。
公式形式如下:1√λ=−2⋅log(ϵ3.7D+2.51Re⋅√λ)其中,ε为绝对粗糙度,D为管道直径,Re为雷诺数。
2.2.3 离散元法离散元法是一种基于数值计算的方法,可以模拟管道内流体传输过程中的微观细节,得到更精确的沿程阻力系数。
该方法需要借助计算机进行模拟和计算,适用于复杂的流体运动情况。
三、沿程阻力系数的影响因素3.1 管道材质管道材质的不同导致其内表面的粗糙度不同,粗糙度对沿程阻力系数有重要影响。
光滑的内表面能减小摩擦阻力,从而减小沿程阻力系数。
3.2 管道直径管道直径的大小会影响雷诺数的大小,进而影响沿程阻力系数的计算。
较大直径的管道有较低的沿程阻力系数。
3.3 流体性质流体的黏度和密度也是影响沿程阻力系数的重要因素。
黏度越大,沿程阻力系数越大;密度越大,沿程阻力系数越小。

紊流的沿程阻力系数
(In-Stream order resistance coefficient K_2)
可以使用静力学理论来计算沿流阻力系数K_2。
静力学理论是一种物理学的分析方法,它以流体的压力分配为基础,用于研究流体的结构以及流体之间的相互作用。
根据静力学原理,沿程阻力系数K_2表示流体在不同压力之间流动时产生的阻力程度,压力加上K_2为流体运动的最终结果。
K_2系数受流体流经的形状、粗糙度和不同材料等多种因素的影响,因此K_2值会随着外力及流体运动速度的变化而不同。
一般来说,K_2值越小,表明沿程抗力越弱,流体流动越容易。
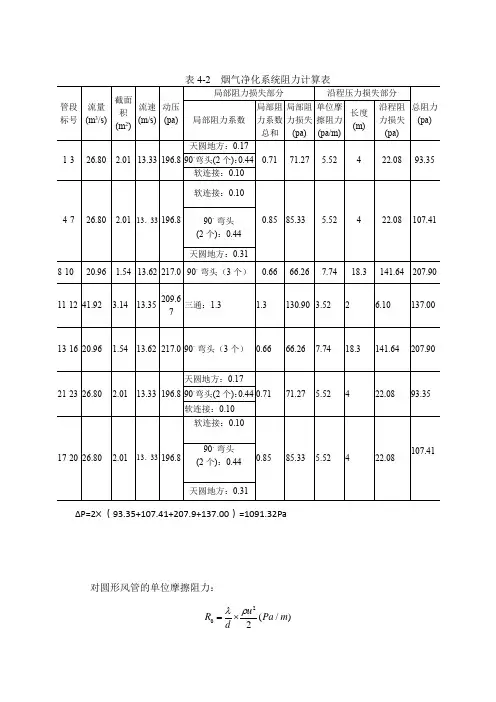

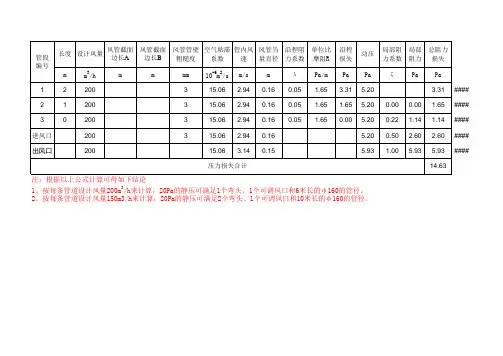
风管沿程阻力计算方法布质风管系统在沿管长方向上还有由于摩擦阻力和局部阻力造成的压力损失。
因为压力损失与风速成正比关系,当气流沿管长方向风速越来越小时,阻力损失也不断下降。
与此同时,风管个标准件以及出风口也存在局部阻力损失。
布质风管系统中以直管为主,系统中三通、弯头及变径很少,一般以沿程阻力损失为主,空气横断面形状不变的管道内流动时的沿程摩擦阻力按下式计算:——摩擦阻力系数;——风管内空气的平均流速,m/s;——空气的密度,kg/m3;——风管长度,m;——圆形风管直径(内径),m;摩擦阻力系数是一个不定值,它与空气在风管内的流动状态和风管管壁的粗糙度有关。
根据对纤维材料和布质风管系统的综合性研究得到摩擦阻力系数不大于0.024(铁皮风管大约0.019),由于布质风管风管延长度方向上都有送风孔,管内平均风速就是风管入口速度的1/2。
由此可见,布质风管风管的延程损失比传统铁皮风管要小的多。
部件局部压损计算当布质风管风管内气流通过弯头、变径、三通等等部件时,断面或流向发生了变化,同传统风管一样会产生相应的局部压力损失:Z:局部压力损失(pa)ξ:局部阻力系数(主要由试验测得,同传统风管中类似)ρ:空气密度(kg/m3)v:风速(m/s)为了减少布质风管系统的局部损失,我们通常进行一定的优化设计:1.综合多种因素选择管经,尽量降低管道内风速。
2.优化异形部件设计,避免流向改变过急、断面变化过快。
根据实际工程经验,我们总结出各种布质风管部件的局部阻力值(风速=8m/s),如下表:弯头(曲率=1)等径三通变径(渐缩角30度)静压箱10 pa 12 pa 3 pa 46 pa例如:某超市压损计算说明对于该超市,AHU 空调箱风量为36000CMH,选取编号AHU-14号空调箱系统,主管尺寸为2000*610mm,共有5支支管,支管管径为55 9mm。
选取最长不利环路25米主管+20.6米支管作为计算依据;1,沿程阻力损失计算:主管:25米,2000*610mm,当量直径,支管道:20.6米,559mm,,2,局部阻力损失计算:等径三通局部损失为12Pa,对于变径三通取20Pa.最长不利环路压损为20+8.5+6=34.5Pa.可见布质风管系统尤其是直管系统的沿程阻力损失非常小,一般不会超过静压复得的值,所以在粗算时基本可以忽略不计!。
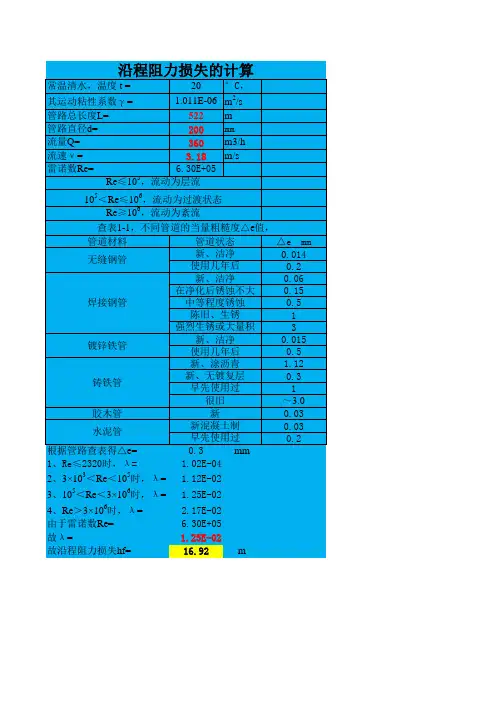
达西公式沿程损失一、达西公式的基本形式。
达西公式为h_f = λ(l)/(d)frac{v^2}{2g},其中:- h_f:沿程损失水头(单位:m),表示流体在管道中流动时由于粘性等因素沿流程产生的能量损失。
- λ:沿程阻力系数,是一个无因次量,其大小与流体的流动状态(层流或紊流)、管壁的粗糙度等因素有关。
- l:管道长度(单位:m),管道越长,沿程损失一般越大。
- d:管道直径(单位:m),管径越小,相对的沿程损失会越大。
- v:管道中流体的平均流速(单位:m/s),流速越大,沿程损失也越大。
- g:重力加速度(g = 9.81m/s^2)。
二、沿程阻力系数λ1. 层流时的λ值。
- 对于层流(Re≤2000,Re=(vd)/(ν)为雷诺数,ν为运动粘度),沿程阻力系数λ=(64)/(Re)。
- 这表明在层流状态下,沿程阻力系数仅与雷诺数有关,与管壁粗糙度无关。
2. 紊流时的λ值。
- 紊流(Re > 2000)时情况较为复杂。
- 当管壁相对光滑(光滑管区)时,λ可由布拉修斯公式λ=(0.3164)/(Re^0.25)计算,该公式适用于Re = 3000 - 10^5的范围。
- 对于粗糙管区,λ与雷诺数和相对粗糙度(Δ)/(d)(Δ为管壁绝对粗糙度)有关。
例如,尼古拉兹公式等可用于计算不同情况下的λ值。
三、达西公式的应用。
1. 管道系统水力计算。
- 在已知管道长度l、直径d、流体流速v、流体性质(以确定λ)的情况下,可以计算沿程损失h_f。
这对于设计管道系统,确定所需的泵扬程等非常重要。
例如,在给水工程中,计算从水源到用户的沿程水头损失,以确保有足够的压力将水输送到用户处。
2. 分析流动阻力对系统的影响。
- 通过达西公式可以分析不同因素(如管径变化、流速变化、管道粗糙度变化等)对沿程损失的影响。
例如,如果要减少沿程损失,可以增大管径(因为管径d在分母上),或者降低流速(流速v的平方与沿程损失成正比)。
尼古拉兹(J.Nikuradse)实验
•实验目的:为了确定λ=f(Re, ε/d)的变化规律。
德国学者(J.Nikuradse,1933-1934)首次进行了实验研究,具有重大的理论意义。
•实验方案:用人工制成的均匀颗粒粗糙圆管,考察6种不同的相对粗糙度的圆管中测出不同流速υ 、管长l 间的水头损失 h f 和水温,以推算Re=υd/ν 和沿程阻力系数λ。
•实验结果: 发现5个有显著规律的区域,揭示了λ=f(Re, ε/d)的影响关系。
1)层流区: λ=64/Re; 2)层-紊流过渡区; 3)光滑管区; 4)光滑管向粗糙管过渡区; 5)粗糙管区
工业管道实验——Moody 图
尼古拉兹实验揭示了管道流动的沿程阻力所产生的能量损失的规律,给出了沿程阻力系数λ与雷诺数Re和相对粗糙度ε/d之间的依变关系,为管道的沿程阻力的计算提供了可靠的实验基础。
但是尼古拉兹实验曲线是在人工地把均匀的砂粒粘贴在管道内壁的情况下实验得出的,然而工业上所用的管道内壁的粗糙度则是自然的非均匀的和高低不平的。
因此,要把尼古拉兹曲线应用于工业管道,就必须作适当的修正。
在工业管道上应用比较广泛的是下面将要介绍的莫迪曲线图。
1944,英国人Moody 对各种工业管道进行了试验 1944
研究。
试验用的管道非常广泛,有:玻璃管、混凝土管、钢管、铜管、木管等,试验条件就是自然管道,管道的壁面就是天然管壁,而非人工粗糙面。
在模型图中可以找到沿管道的阻力系数,即λ、re和K/D的关系曲线,这是液压系统中常用的。
K是管内壁的绝对粗糙度。
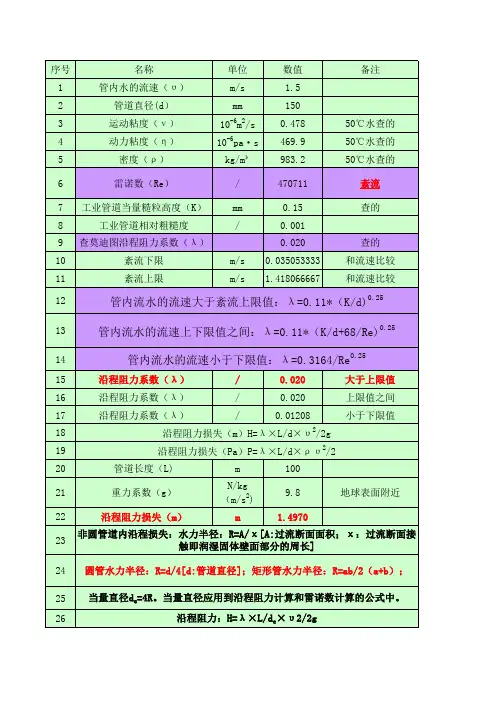
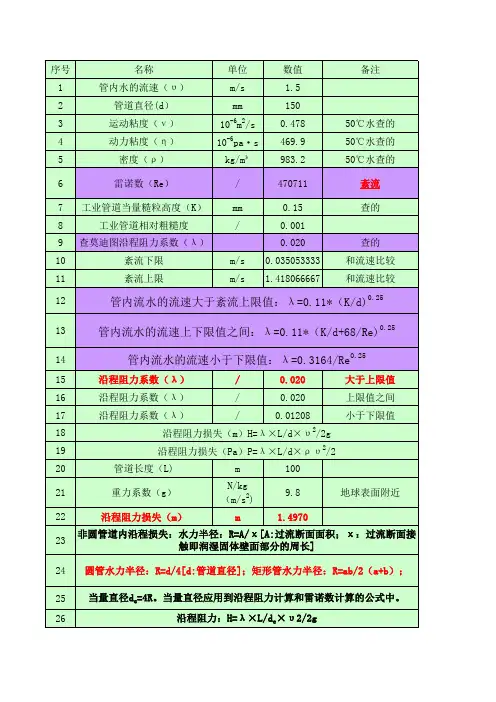
管道沿线水头损失计算:H=λ(L/D)[v^2/(2G)]
对于管内层流:λ=64/re(雷诺数re=VD/ν)
圆管粗糙过渡区:1/√(λ)=-2*LG[K/(3.7d)+2.51/re√(λ)]
对于管的湍流粗糙区:1/√(λ)=-2*LG[K/(3.7d)]也可用作λ=0.11(K/D)^0.25还有许多经验公式:
例如,钢管和铸铁管的Shevlev公式为:过渡粗糙区(V<1.2m/s):λ=(0.0179/D^0.3)*(1+0.867/V)^0.3;阻力平方面积(V>=1.2m/s):λ=0.21/D^0.3
摩擦阻力:流体流经一定直径的直管时,由于流体的内摩擦而产生阻力。
电阻与距离的长度成正比。
简介
在计算管道沿程阻力损失(直管阻力)的公式中,λ-摩擦系数与雷诺数Re和壁面粗糙度ε有关,可以通过实验测量或计算。
层流
如何确定一个通道的阻力系数
对于层流,可以从理论上严格推断。
在工程中,湍流的确定有两种方法:一种是基于湍流半经验理论结合实验结果,另一种是直接根据实验结果综合阻力系数的经验公式。
前者具有更一般的含义。
沿途阻力系数变化规律3-8计算沿途水头损失的经验公式3-3--8沿途水头损失的经验公式3-9局部水头损失3-9局部水头损失3-7沿程阻力系数的变化规律可从本章各节中了解。
对于层流,沿程阻力系数的规律是已知的。
到目前为止,还没有一个沿程阻力系数的理论公式。
为了探索沿程阻力系数的变化规律,尼古拉斯进行了一系列实验研究,揭示了沿途水头损失的规律。
下面介绍这一重要的实验研究成果。
1尼古拉斯试验条件。
管道的人工粗糙表面:在管壁上粘上相同尺寸的均匀砂粒。
注:此粗糙表面与天然粗糙表面完全不同。
相对粗糙度:Δ/r0相对平滑度:r0/ΔΔ=dr0沿途阻力系数试验装置。