《信号与系统》考研试题解答第二章连续系统的时域分析
- 格式:docx
- 大小:116.89 KB
- 文档页数:16

X2.1 (东南大学2002年考研题)一线性时不变连续时间系统,其在某激励信号作用下的自由响应为(e-3t+e-t) (t),强迫响应为(1-e-2t) (t),则下面的说法正确的是______________(A)该系统一定是二阶系统(B)该系统一定是稳定系统(C)零输入响应中一定包含(e-3t+e-t) (t)(D )零状态响应中一定包含(1-e-2t) (t)X2.2(西安电子科技大学2005年考研题)信号f1(t)和f2(t)如图X2.2所示,f=f1(t)* f2(t),则f(-1)等于__________图X2.2X2.3 (西女电子科技大学2005年考研题)下列等式不成立的是(A) f1(t t。
)* f2(t t°) 锂) * f2(t)(B)-J—f1(t)* f2(t) dtd f1(t)dt-J* — f2(t) dt 2(C) f(t)* (t) f (t)(D) f(t)* (t) f (t)答案:X2.1[D] , X2.2[C], X2.3[B]、判断与填空题T2.1 (北京航空航天大学2001年考研题)判断下列说法是否正确,正确的打错误的打“X” 。
(1 )若y(t) f(t)*h(t),则y(2t) 2f(2t)*h(2t)。
[](2)如果x(t)和y(t)均为奇函数,贝U x(t)*y(t)为偶函数。
[](3)卷积的方法只适用于线性时不变系统的分析。
[](4 )若y(t) f(t)*h(t),则y( t) f( t)*h( t)。
[](5)两个LTI系统级联,其总的输入输出关系与它们在级联中的次序没有关系。
[]第二章、单项选择题连续系统的时域分析(C) 1.5 ( D)-0.5(A)T2.2 (华中科技大学2004年考研题)判断下列叙述或公式的正误,正确的在方括号中打“/,错误的在方括号中打“X”。
(1)线性常系数微分方程表示的系统,其输出响应是由微分方程的特解和齐次解组成,或由零输入响应和零状态响应所组成。



![信号与系统第2章 连续时间信号与系统的时域分析[精]](https://uimg.taocdn.com/f309c644dd36a32d7275811e.webp)

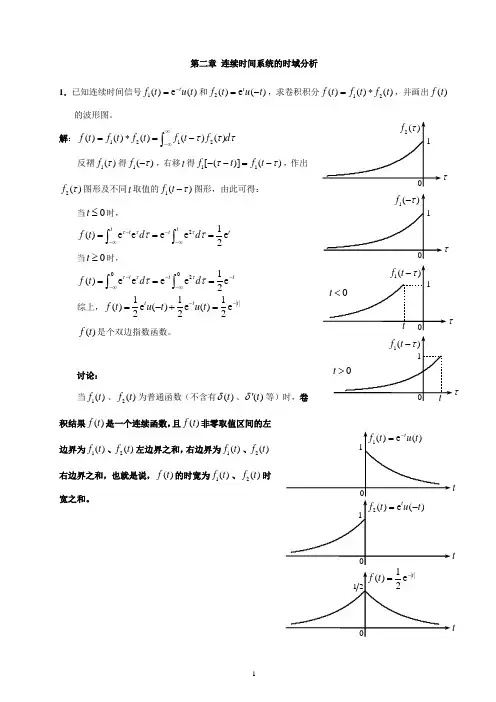
第二章 连续时间系统的时域分析1.已知连续时间信号1()e ()t f t u t -=和2()e ()t f t u t =-,求卷积积分12()()()f t f t f t =*,并画出()f t 的波形图。
解:1212()()()()()f t f t f t f t f d τττ∞-∞=*=-⎰反褶1()f τ得1()f τ-,右移t 得11[()]()f t f t ττ--=-,作出2()f τ图形及不同t 取值的1()f t τ-图形,由此可得:当0t ≤时,21()e e ee e 2ttt tt f t d d τττττ---∞-∞===⎰⎰当0t ≥时,0021()e e e e e 2t t t f t d d τττττ----∞-∞===⎰⎰综上,||111()e ()e ()e 222t t t f t u t u t --=-+=()f t 是个双边指数函数。
讨论:当1()f t 、2()f t 为普通函数(不含有()t δ、()t δ'等)时,卷积结果()f t 是一个连续函数,且()f t 非零取值区间的左边界为1()f t 、2()f t 左边界之和,右边界为1()f t 、2()f t 右边界之和,也就是说,()f t 的时宽为1()f t 、2()f t 时宽之和。
τttt2.计算题图2(a )所示函数)(1t f 和)(2t f 的卷积积分)()()(21t f t f t f *=,并画出)(t f 的图形。
解法一:图解法1212()()()()()f t f t f t f t f d τττ∞-∞=*=-⎰其中1()f t τ-的波形见题图2(b),由此可得: 当10t +≤,即1t ≤-时,()0f t = 当011t ≤+≤,即10t -≤≤时,120()2(1)t f t d t ττ+==+⎰当11t +≥但10t -≤,即01t ≤≤时,1()21f t d ττ==⎰当011t ≤-≤,即12t ≤≤时,121()21(1)t f t d t ττ-==--⎰当11t -≥,即2t ≥时,()0f t =综上,220,1,2(1),10()1,011(1),12t t t t f t t t t ≤-≥⎧⎪+-≤≤⎪=⎨≤≤⎪⎪--≤≤⎩ ()f t 波形见题图2(c)。



— P2-1 —第二章 连续系统的时域分析习题解答2-1 图题2-1所示各电路中,激励为f (t ),响应为i 0(t )和u 0(t )。
试列写各响应关于激励微分算子方程。
解:.1)p ( ; )1(1)p ( , 111 , 1111)( )b (;105.7)625(3 102 ;)(375)()6253(4)()()61002.041( )a (0202200204006000f i p f p u p f p p p u i f p p p ppft u pf i p pu i t f t u p t f t u p =+++=++⇒++=+=+++=++=⨯=+⇒⨯==+⇒=++-- 2-2 求图题2-1各电路中响应i 0(t )和u 0(t )对激励f (t )的传输算子H (p )。
解:.1)()()( ; 11)()()( )b (;6253105.7)()()( ; 6253375)()()( )a (220 20 40 0 +++==+++==+⨯==+==-p p p p t f t i p H p p p t f t u p H p p t f t i p H p t f t u p H f i f u f i fu2-3 给定如下传输算子H (p ),试写出它们对应的微分方程。
.)2)(1()3()( )4( ; 323)( )3(; 33)( )2( ; 3)( )1( +++=++=++=+=p p p p p H p p p H p p p H p p p H解:; 3d d 3d d )2( ; d d 3d d)1( f tf y t y t f y t y +=+=+ . d d 3d d 2d d 3d d )4( ; 3d d 3d d 2 )3( 2222t f tf y t y t y f t f y t y +=+++=+ 2-4 已知连续系统的输入输出算子方程及0– 初始条件为:.4)(0y ,0)(0y )y(0 ),()2(13)( )3(; 0)(0y ,1)(0y ,0)y(0 ),()84()12()( )2(;1)(0y ,2)y(0 ),()3)(1(42)( )1(---2---2--=''='=++==''='=+++-=='=+++=t f p p p t y t f p p p p t y t f p p p t yf (u 0(t ) (b) u 0(t ) (a)图题2-1— 2 —试求系统的零输入响应y x (t )(t /0)。
第二章 连续系统的时域分析、单项选择题X2.1 (东南大学2002年考研题)一线性时不变连续时间系统,其在某激励信号作用下的自由响应为(e-3t+e -t ) (t),强迫响应为 ・2t(1-e ) ;(t),则下面的说法正确的是(A )该系统一定是二阶系统(B) 该系统一定是稳定系统 (C) 零输入响应中一定包含 (e-3t+e -t ) ;(t) (D )零状态响应中一定包含 (1-e-2t) (t)X2.2 (西安电子科技大学2005年考研题)则f(-1)等于 _________ 。
图 X2.2X2.3(西女电子科技大学 2005年考研题) 下列等式不成立的是(A) 皿-鮎)* f 2(t t 。
)= f't)* f 2(t)(B) 沪f1⑴* M 汪f1⑴*炸 f 2(t)(C) f(t)*、(t)= f ⑴(D) f(t)*、(t)= f(t)答案: X2.1[D] , X2.2[C] , X2.3[B]、判断与填空题T2.1 (北京航空航天大学 2001年考研题)判断下列说法是否正确,正确的打,错 误的打“x”。
(1 )若 y(t) = f (t)* h(t),则 y(2t) =2f (2t)* h(2t)。
[](2) 如果x(t)和y(t)均为奇函数,贝U x(t)*y(t)为偶函数。
[](3)卷积的方法只适用于线性时不变系统的分析。
[](4)若 y(t) = f(t)*h(t),则 y(-t)二 f(-t)*h(-t)。
[](5)两个LTI 系统级联,其总的输入输出关系与它们在级联中的次序没有关系。
[](a)(C ) 1.5 ( D ) -0.5信号 f i (t)和 f 2(t)如图 X2.2 所示,f =f i (t)*,T2.2 (华中科技大学2004年考研题)判断下列叙述或公式的正误,正确的在方括号中打“/,错误的在方括号中打“X”。
(1)线性常系数微分方程表示的系统,其输出响应是由微分方程的特解和齐次解组成,或由零输入响应和零状态响应所组成。
齐次解称之为自由响应[],特解称之为强迫响应[];零输入响应称之为自由响应[],零状态响应称之为强迫响应[]。
(2)(上海交通大学2000年考研题)f(t)「(tr f(t)[]f(t) (\)= f(0)[]t—()d "[]tf( .)d. = f (t)* ;(t)[]T2.3在下列各题的横线上填上适当的内容:(1) (北京邮电大学2000年考研题)—e * =(t)Ldt ---------t(2) (国防科技大学2001年考研题) …f(.)d.二f(t)*_ **^0 " =T2.4 (华南理工大学2004年考研题)一连续LTI系统的单位阶跃响应g(t)二e" ;(t), 则该系统的单位冲激响应为h(t)= ________________________ 。
T2.5 (华南理工大学2004年考研题)已知信号h(t)= ;(t-1)- ;(t-2), f(t)= (t-2)-往4),则卷积f (t)* h(t) = ___________________ 。
T2.6 (南京理工大学2000年考研题)某系统如图T2 . 6所示,若输入□0f(t) :(t -nT),则系统的零状态响应为_________________n =0图T2 . 6T2.7 (北京交通大学2004年考研题)对连续信号延迟t0的延时器的单位阶冲激应为__________ ,积分器的单位阶冲激应为____________ ,微分器的单位阶冲激应为___________ 答案:T2.1 (1 )V ( 2)V ( 3)V (4)V (5)VT2.2 (1 )V,V,X,X ( 2)V,X,X,V-2tT2.3 (1) e (2) (t)-3tT2.4 h(t)=、⑴-3e (t)T2.5 h(t)*f(t)= (t-3) <t-3) - (t-4) (t-4) - (t-5) (t-5) (t-6) (t-6)T2.6 ⑴T2.7 、(t-t o), ⑴(t)三、画图、证明与分析计算题J2.1 (东南大学2001年考研题)已知某线性系统可以用以下微分方程描述y (t) 6y (t) 5y(t) = 9f (t) 5f (t)系统的激励为f(t)= (t),在t=0和t=1时刻测量得到系统的输出为y(0)=0, y(1)=1-e-5。
(1)求系统在激励下的全响应,并指出响应中的自由响应、强迫响应、零输入响应、零状态响应分量;(2)画出系统模拟框图。
解:(1)先求系统的冲激响应h(t)。
h(t)应满足以下微分方程:h (t) 6h (t) 5h(t^9 (t) 5 (t) (J2.1-1)设h1(t)满足微分方程:hi(t) 6h1(t) 5h(t) (t) (J2.1 -2) 贝V h(t) =9h(t) 5g(t) (J2.1—3)由式(J2.1 -2)求h«t):特征方程:九2+6二+5 =0特征根:- -1, '2 - -5贝V h(t)二Ae 叭A2e2t;(t)二Ae」;(t)下面求系数A、A2。
由式(J2.1-2)微分方程可知:h;(t)中应包含(t)项,则h;(t) 在t =0处不连续,即hdO J 讪0 0 =0; h(t)中不含(t)项,则0(t)在t =0处连续,即h1(0 .) =^(0_) =0°对式(J2.1 _2)微分方程在t =0 _〜0内积分,可得h;(0 .) =1。
利用0初始值h1(0 .) =0, h1(0 ) =1确定系数A、A2:h i (O 』=A 1 + A ? = 0 A 1 = 0.25h /(t) = —A —5A ? =1A? = —0.25故 h ,(t) =0.25e ±-e-t;(t)代入式(J2.1 - 3)可得h(t) =(10e^ _e 丄孰t)则零状态响应为y zs (t) = f(t)*h(t)二1(t 「)10e)-e- ;(.)d. at5=0(10e —^—e Y d i 常⑴=(1 +e±—2e't >(t)由此可得:y zs (0)=(l+e 上—2e't 》(t)y =0y zs (1)=(!+e 丄-2e 仓》(t)仁=1+e 丄—2e'F 面求系统的零输入响 应y zi (t),y zi (t)应满足以下微分方程y z ;(t) 6y z ;(t) 5丫』)=0 则 y/t) = 电⑸;(t)下面求系数B 、B 2 :Yzi (0) = B i + B 2*y/ire ^B ie'B 2y(0) = y zi (0) +y zs (0) = B +B 2 =0 y(1) =y zi (1) y zs (1) =e 」B i e'B 2 1 e 」-2e*=1-B +B 2 =0二丿e^B t +e 』B 2=-e 丄+e 』故 y zi (t) =:€耳—e 丄;(t)则系统的全响应为y(t)二 y zi (t) y zs (t) =(1 —e 「;(t)由上式可知,自由响应y h (t)、强迫响应y p (t)分别为:y h (t)二 v*(t),y p (t)=1(2 )系统框图如下:B = -1 (B 2 = 1图 J2.1-1J2.2 (上海大学2000年考研题)某线性时不变系统的单位阶跃响应为g(t)二3e2t-1 ;(t)用时域解法求:(1 )系统的冲激响应h(t);(2)系统对激励f/t)二t;(t)的零状态响应y zsi(t);(3)系统对激励f2(t) =t〔;(t) - ;(t -1) 1的零状态响应y zs2(t).=dg(t)=2、.(t) -6e't ;(t)解:(i) h(t)dt(2)y zsi(t) = f i(t)* h(t)二f i⑴* h(」)(t) = ;(t)* (3e^t-1);(t)】=f (3e/^—1)名(巧dt =(1.5_t _1.5e』)&(t)J-=O(3)f2(t) =t l;(t) - ;(t -1) =t ;(t) _(t _1) ;(t -1)- ;(t -1)t;(t) > y zsi(t) = 1.5-t-1.5e2 ;(t)(t-1);(t-1) > y zs1(t-1) = 1.5 — (t-1) “.也❾‘门建一1)=2.5_t —i^e^ts L(t -1);(t 一1) > g(t -1) = 3^^(tJ)-^;(t -1)y zs2(t)订{% f2(t)l=T {0}, t ;(t)丨T {0}, -(t -1) ;(t -1)丨T {0}, - ;(t -1)1(t - 1) - g(t - 1)=yzs1 (t) - y zs1二1.5—t —1.5e』;(t) 一1.5—t 1.5e'(2)L(t -1)J2.3 (重庆大学2001年考研题)已知一线性时不变系统的单位冲激响应JI 他、h(t)=—sin —t F(t),输入信号f(t)的波形如图J2.3-1所示。
用时域法求系统的零状态响2 12丿应y zs(t).图J2.3-1解:利用卷积的微积分性质,可得y zs (t) =f(t)*h(t)二 f ⑴(t)*h (」)(t)h (」)(t)二 tt 」()d = 71■:t一sin —丁 i&O d i = 1 - cos — it(t)对输入信号f(t)求一阶导数,如图J2.3-2。
桦)1-110 T Z1618图 J2.3-2oOf ⑴(t) :、(t _6n) _、(t _6n_4) 1oO二 h (」)(t)* ' l (t —6n) -、(t —6n —4)1QO八 h(4(t —6n)—h (4(t —6n-4)cos?(t_6n) ;(t_6 n)_ 1 - co^ (^6 n_4) ;(t ■t 二、1 -^1)n cos- n=0 _2- 6n) - ; (t - 6n - 4)- J2.4 (北京交通大学 2001年考研题)已知一线性时不变系统的单位冲激响应 f(t)的波形如图J2.4-1 (a)、(b)所示。
用时域法求系统的零状态响应y zs (t),画出 -6n - 4)h(t)和激励y zs (t)的波形.2i f(t)21 h(t)tdt1 F212(a)(b)解:为运算方便,分别对 h(t)、f(t)分别求微分和积分,如图J2.4-2。
1__2t1* -2J-图 J2.4-1(a)h '(t) (b)f(J)(t)= / f(E)dm =22(t)—2(t —2"(t —2)h(t) =、(t) 、(t —1) —2、(t —2)y zs(t) = f(t)*h(t)二f(J)(t)*h(t)二f(J)(t) f (J)(t 一1) —2f (J)(t -2)=2t ;(t) 2(t -1) ;(t _1) _6(t -2) ;(t _2) _2(t _3) ;(t_3) 4(t _4) ;(t _4)y zs(t)的波形如图J2.4-3所示。