§5.4 理想低通滤波器

低通滤波器设计原理低通滤波器是一种常用的信号处理技术，用于从信号中去除高频成分，使得信号中只保留低频成分。

其设计原理基于信号的频率特性和滤波器的特性。

一、低通滤波器的基本原理低通滤波器的基本原理是通过选择合适的频率截止点，使得该频率以下的信号通过滤波器，而高于该频率的信号被滤除或衰减。

这样可以实现去除高频噪声或不必要的信号，保留主要的低频信号。

二、滤波器的频率响应滤波器的频率响应是指滤波器对不同频率信号的响应程度。

低通滤波器的频率响应在截止频率以下保持较高的增益，而在截止频率以上逐渐衰减。

具体来说，低通滤波器的频率响应可以用一个截止频率和一个衰减因子来描述。

三、滤波器的类型根据滤波器的特性，低通滤波器可以分为两类：理想低通滤波器和实际低通滤波器。

理想低通滤波器是指在截止频率以下完全通过信号，而在截止频率以上完全抑制信号的滤波器。

实际低通滤波器是指在截止频率以下有一定的增益，而在截止频率以上有一定的衰减的滤波器。

四、滤波器的设计方法1. 传统方法：传统的低通滤波器设计方法包括巴特沃斯滤波器、切比雪夫滤波器和椭圆滤波器。

这些方法通常基于模拟滤波器设计原理，通过选择合适的滤波器阶数和截止频率来实现低通滤波器的设计。

2. FIR滤波器设计：FIR滤波器是一种常用的数字滤波器，其设计方法与传统方法有所不同。

FIR滤波器通过选择合适的滤波器系数来实现低通滤波器的设计。

常用的FIR滤波器设计方法包括窗函数法、最小均方误差法和频率采样法等。

五、滤波器的性能指标低通滤波器的性能指标包括截止频率、衰减因子、通带波动和群延迟等。

截止频率是指滤波器开始衰减的频率，通常用3dB衰减点来定义。

衰减因子是指滤波器在截止频率以上的衰减程度，通常以分贝（dB）为单位来表示。

通带波动是指滤波器在通带范围内的增益波动程度，通常以分贝为单位来表示。

群延迟是指滤波器对不同频率信号的传输延迟，通常以时间为单位来表示。

六、应用领域低通滤波器在各个领域都有广泛的应用。

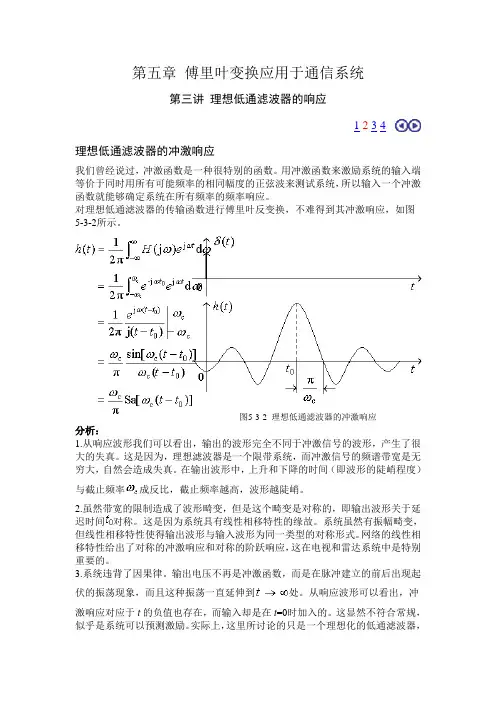
第五章傅里叶变换应用于通信系统第三讲理想低通滤波器的响应1234理想低通滤波器的冲激响应我们曾经说过，冲激函数是一种很特别的函数。

用冲激函数来激励系统的输入端等价于同时用所有可能频率的相同幅度的正弦波来测试系统，所以输入一个冲激函数就能够确定系统在所有频率的频率响应。

对理想低通滤波器的传输函数进行傅里叶反变换，不难得到其冲激响应，如图5-3-2所示。

图5-3-2 理想低通滤波器的冲激响应分析：1.从响应波形我们可以看出，输出的波形完全不同于冲激信号的波形，产生了很大的失真。

这是因为，理想滤波器是一个限带系统，而冲激信号的频谱带宽是无穷大，自然会造成失真。

在输出波形中，上升和下降的时间（即波形的陡峭程度）与截止频率成反比，截止频率越高，波形越陡峭。

2.虽然带宽的限制造成了波形畸变，但是这个畸变是对称的，即输出波形关于延迟时间对称。

这是因为系统具有线性相移特性的缘故。

系统虽然有振幅畸变，但线性相移特性使得输出波形与输入波形为同一类型的对称形式。

网络的线性相移特性给出了对称的冲激响应和对称的阶跃响应，这在电视和雷达系统中是特别重要的。

3.系统违背了因果律。

输出电压不再是冲激函数，而是在脉冲建立的前后出现起伏的振荡现象，而且这种振荡一直延伸到处。

从响应波形可以看出，冲激响应对应于t的负值也存在，而输入却是在t=0时加入的。

这显然不符合常规，似乎是系统可以预测激励。

实际上，这里所讨论的只是一个理想化的低通滤波器，它的响应特性在物理上是不可实现的。

系统的物理可实现性——佩利-维纳准则虽然理想低通滤波器在实际中是不能实现的，但是我们希望找到一种区分可实现性与不可实现性的标准，这就是佩利-维纳（Paley-Wiener）准则。

物理可实现性在文献中有不同定义方法，这里采用最低限度的定义把物理可实现性系统和不可实现系统区分开来。

我们可以直观地看到，一个物理可实现系统在激励加入之前是不可能有响应输出的，这称为因果条件。

理想滤波器传递函数推导【摘要】理想滤波器是信号处理中常用的一种滤波器，通过频域的方式对信号进行处理。

本文将通过推导的方式介绍理想滤波器的传递函数。

我们会分别推导理想低通、高通、带通和带阻滤波器的传递函数，以展示不同类型滤波器的频率特性。

通过这些推导，读者将能够更好地理解不同类型滤波器在频域上的表现。

在结论中将对理想滤波器传递函数进行总结，强调其在信号处理中的重要性和应用价值。

通过本文的阐述，读者将能够更全面地理解理想滤波器传递函数的推导过程和作用。

【关键词】理想滤波器、传递函数、推导、低通、高通、带通、带阻、引言、结论1. 引言1.1 理想滤波器传递函数推导理想滤波器是一种理论上的滤波器，能够完美地通过某些频率的信号，同时完全阻断其他频率的信号。

通过推导理想滤波器的传递函数，我们可以更好地理解其工作原理以及性能特点。

传统上，滤波器可以分为低通滤波器、高通滤波器、带通滤波器和带阻滤波器。

对于理想滤波器，其传递函数的推导也分别对应着这四种类型的滤波器。

在推导理想滤波器传递函数时，我们首先要给出该滤波器的频率响应特性。

对于理想低通滤波器，频率响应在截止频率之前完全透过信号，在截止频率之后完全阻断信号。

这种频率响应可以用数学表示进行推导。

通过推导理想滤波器的传递函数，我们可以深入理解滤波器的工作原理，为实际滤波器设计提供参考，并通过理论分析优化滤波器性能。

理想滤波器传递函数的推导是滤波器理论研究中的重要一步，为滤波器设计与应用提供了重要基础。

2. 正文2.1 理想低通滤波器传递函数推导理想低通滤波器是一种在频域上将低频信号通过，高频信号截断的滤波器。

其传递函数推导过程如下：设理想低通滤波器的频率响应为H(f)，滤波器的输入信号为x(t)，输出信号为y(t)，则有：\[ H(f) =\begin{cases}1, & \text{if } |f| \leq f_c\\0, & \text{otherwise}\end{cases}\]\(f_c\)为滤波器的截止频率。

3-2-1 计算理想低通滤波1 计算理想低通滤波器的)(n h a 函数ideal_lp 设所要求的理想数字滤波器的频率响应为)(e H jwd ，h d（n ）是与其对应的单位脉冲响应，因此dw n ee H h jwnjw d d⎰-=πππ)(21)(由于)(e H jwd 是矩形频率特性，故h d（n ）一定是无限长的非因果序列。

而所要设计的是FIR 数字滤波器，其单位脉冲响应h （n ）必然是有限长的，所以要用有限的h （n ）来逼近无限长的h d （n ），最有效的方法是截断h d （n ），即用有限长的窗函数来截取h d （n ）， 表示为： h （n ）＝h d （n ）w （n ） 这种设计方法称为窗函数设计法。

数字低通滤波器的窗函数设计理想低通数字滤波器的频率响应)(e H jwd 为：⎪⎩⎪⎨⎧>≥≤⋅=-w w e e H cc jwajw d w w ||0||1)(π，，式中w c——截至频率，rad ；a ——采样延迟。

则理想数字低通滤波器的单位脉冲响应h d （n ）为[])()(sin 121)(21)(a n a n dw w w dwn w e e ee H h c jwnjwa jwnjw d d c c --=⋅-⋅==⎰⎰--πππππh d （n ）为无限长非因果序列，关于a 偶对称。

为了从h d （n ）得到一个FIR 数字滤波器，必须同时在两边截取h d （n ），要得到一个因果的线性相位FIR 滤波器，它的h （n ）的长度为N ，必须有⎪⎩⎪⎨⎧≤≤=，其它－，01N n 0)()(n n h h d a ＝21-N这种截取可看作是 h （n ）＝h d （n ）w （n ）其中 ⎩⎨⎧≤≤=，其它－，01N n 01)(n w 矩形窗h （n ）为关于a 偶对称的有限长因果序列，N 为奇数时是1型，N 为偶数时是2型。

在MATLAB 中利用ideal_lp 函数，计算理性低通滤波器的单位脉冲响应h d （n ）。