2010年中考数学试题分类汇编_二次函数(含详细解答)人教新课标版

28．（2010广东中山）如图（1），（2）所示，矩形ABCD 的边长AB=6，BC=4，点F 在DC 上，DF=2．动点M 、N 分别从点D 、B 同时出发，沿射线DA 、线段BA 向点A 的方向运动（点M 可运动到DA 的延长线上），当动点N 运动到点A 时，M 、N 两点同时停止运动．连接FM 、MN 、FN ，当F 、N 、M 不在同一直线时，可得ΔFMN ，过ΔFMN 三边的中点作ΔPQW ．设动点M 、N 的速度都是1个单位/秒，M 、N 运动的时间为x 秒．试解答下列问题： （1）说明ΔFMN ∽ΔQWP ；（2）设0≤x ≤4（即M 从D 到A 运动的时间段）．试问x 为何值时，ΔPQW 为直角三角形？当x 在何范围时，ΔPQW 不为直角三角形？（3）问当x 为何值时，线段MN 最短？求此时MN 的值．．【答案】解：（1）由题意可知P 、W 、Q 分别是ΔFMN 三边的中点， ∴PW 是ΔFMN 的中位线，即PW ∥MN ∴ΔFMN ∽ΔQWP（2）由题意可得 DM=BN=x ，AN=6-x ，AM=4-x ， 由勾股定理分别得 2FM =24x +，2MN =2)4(x -+2)6(x - 2FN =2)4(x -+16①当2MN =2FM +2FN 时，2)4(x -+2)6(x -=24x ++2)4(x -+16 解得 34=x ②当2FN =2FM +2MN 时，2)4(x -+16=24x ++2)4(x -+2)6(x - 此方程无实数根③2FM =2MN +2FN 时，24x +=2)4(x -+2)6(x -+2)4(x -+16 解得 101=x （不合题意，舍去），42=x 综上，当34=x 或4=x 时，ΔPQW 为直角三角形；当0≤x ＜34或34＜x ＜4时，ΔPQW 不为直角三角形 （3）①当0≤x ≤4，即M 从D 到A 运动时，只有当x=4时，MN 的值最小，等于2； ②当4＜x ≤6时，2MN =2AM +2AN =2)4(-x +2)6(x -=2)5(22+-x当x=5时，2MN 取得最小值2， ∴当x=5时，线段MN 最短，MN=2． 29．（2010湖南常德）如图9, 已知抛物线212y x bx c =++与x 轴交于A (－4，0) 和B (1，0)两点，与y 轴交于C 点．（1）求此抛物线的解析式；（2）设E 是线段AB 上的动点，作EF //AC 交BC 于F ，连接CE ，当△CEF 的面积是△BEF面积的2倍时，求E 点的坐标;（3）若P 为抛物线上A 、C 两点间的一个动点，过P 作y 轴的平行线，交AC 于Q ，当P点运动到什么位置时，线段PQ 的值最大，并求此时P 点的坐标．【答案】解：（1）由二次函数212y x bx c =++与x 轴交于(4,0)A -、(1,0)B 两点可得：221(4)4021102b c b c ⎧--+=⎪⎪⎨⎪⋅++=⎪⎩，． 解得： 322b c ⎧=⎪⎨⎪=-⎩，．故所求二次函数的解析式为213222y x x =+-．（2）∵S △CEF =2 S △BEF , ∴1,2BF CF =1.3BF BC =∵EF //AC , ∴B ,EF BAC BFE BCA ∠=∠∠=∠ ,∴△BEF ～△BAC ,∴1,3BE BF BA BC ==得5,3BE = 故E 点的坐标为(23-,0).xyO BC A图9（3）解法一：由抛物线与y 轴的交点为C ，则C 点的坐标为（0，－2）．若设直线AC的解析式为y kx b =+，则有20,04b k b -=+⎧⎨=-+⎩． 解得：1,22k b ⎧=-⎪⎨⎪=-⎩．故直线AC 的解析式为122y x =-－．若设P 点的坐标为213,222a a a ⎛⎫+- ⎪⎝⎭，又Q 点是过点P 所作y 轴的平行线与直线AC 的交点，则Q 点的坐标为（1,2)2a a --．则有：2131[(2)](2)222PQ a a a =-+----＝2122a a --＝()21222a -++即当2a =-时，线段PQ 取大值，此时P 点的坐标为（－2，－3） 解法二：延长PQ 交x 轴于D 点，则PD AB ⊥．要使线段PQ 最长，则只须△APC的面积取大值时即可.设P 点坐标为（),00y x ，则有:ACO DPCO SAPCADPSSS =+-梯形＝111()222AD PD PD OC OD OA OC ⋅++⋅-⋅ ＝()()000001112242222x y y y x --+-+⋅--⨯⨯＝0024y x ---＝20001322422x x x ⎛⎫-+--- ⎪⎝⎭＝2004xx -- ＝－()22024x ++即02x =-时，△APC 的面积取大值，此时线段PQ 最长，则P 点坐标为（－2，－3）30 ．（2010湖南郴州）如图（1），抛物线42y x x =+-与y 轴交于点A ，E （0，b ）为y 轴上一动点，过点E 的直线y x b =+与抛物线交于点B 、C .（1）求点A 的坐标； （2)当b =0时（如图（2）），ABE 与ACE 的面积大小关系如何？当4b >-时，上述关系还成立吗，为什么？（3）是否存在这样的b ，使得BOC 是以BC 为斜边的直角三角形，若存在，求出b ；若不存在，说明理由.【答案】（1）将x =0，代入抛物线解析式，得点A 的坐标为（0，－4） （2）当b ＝0时，直线为y x =，由24y xy x x =⎧⎨=+-⎩解得1122x y =⎧⎨=⎩，2222x y =-⎧⎨=-⎩所以B 、C 的坐标分别为（－2，－2），（2，2）14242ABES=⨯⨯=，14242ACES =⨯⨯= 所以ABEACE S S=当4b >-时，仍有ABEACE SS=成立.理由如下由24y x b y x x =+⎧⎨=+-⎩，解得11x y b ⎧=⎪⎨=⎪⎩，22x y ⎧=⎪⎨=⎪⎩所以B 、C b 作BF y ⊥轴，CG y ⊥轴，垂足分别为F 、G ，则而ABE 和ACE 是同底的两个三角形， 所以ABEACE SS=.（3）存在这样的b .因为90BF CG,BEF CEG,BFE CGE =∠=∠∠=∠=︒ 所以BEF CEG ≅所以BE CE =，即E 为BC 的中点所以当OE =CE 时，OBC 为直角三角形 因为GE b b GC =-== 所以 CE =OE b =b =，解得124,2b b ==-，所以当b ＝4或－2时，ΔOBC 为直角三角形.31．（2010湖南怀化）图9是二次函数k m x y ++=2)(的图象，其顶点坐标为M(1,-4). （1）求出图象与x 轴的交点A,B 的坐标； （2）在二次函数的图象上是否存在点P ，使MAB PAB S S ∆∆=45,若存在，求出P 点的 坐标；若不存在，请说明理由；（3）将二次函数的图象在x 轴下方的部分沿x 轴翻折，图象的其余部分保持不变， 得到一个新的图象，请你结合这个新的图象回答：当直线)1(<+=b b x y 与此 图象有两个公共点时，b 的取值范围.【答案】解;(1) 因为M(1,-4) 是二次函数k m x y ++=2)(的顶点坐标，所以324)1(22--=--=x x x y 令,0322=--x x 解之得3,121=-=x x . ∴A ，B 两点的坐标分别为A （-1，0），B （3,0） (2) 在二次函数的图象上存在点P ，使MAB PAB S S ∆∆=45设),,(y x p 则y y AB S PAB 221=⨯=∆，又8421=-⨯=∆AB S MAB , ∴.5,8452±=⨯=y y 即 ∵二次函数的最小值为-4，∴5=y . 当5=y 时，4,2=-=x x 或.故P 点坐标为（-2，5）或（4，5）……………7分 （3）如图1，当直线)1(<+=b b x y 经过A 点时，可得.1=b ……………8分图9图1当直线)1(<+=b b x y 经过B 点时，可得.3-=b由图可知符合题意的b 的取值范围为13<<-b 32．（2010湖北鄂州）如图，在直角坐标系中，A （-1，0），B （0，2），一动点P 沿过B 点且垂直于AB 的射线BM 运动，P 点的运动速度为每秒1个单位长度，射线BM 与x 轴交与点C ．（1）求点C 的坐标．（2）求过点A 、B 、C 三点的抛物线的解析式．（3）若P 点开始运动时，Q 点也同时从C 出发，以P 点相同的速度沿x 轴负方向向点A 运动，t 秒后，以P 、Q 、C 为顶点的三角形为等腰三角形．（点P 到点C 时停止运动，点Q 也同时停止运动）求t 的值． （4）在（2）（3）的条件下，当CQ =CP 时，求直线OP 与抛物线的交点坐标．【答案】（1）点C 的坐标是（4，0）；（2）设过点A 、B 、C 三点的抛物线的解析式为y =ax 2+bx +c （a ≠0），将点A 、B 、C 三点的坐标代入得：020164a b c c a b c =-+⎧⎪=⎨⎪=++⎩解得12322a b c ⎧=-⎪⎪⎪=⎨⎪=⎪⎪⎩，∴抛物线的解析式是：y = 12-x 2+32x +2． （3）设P 、Q 的运动时间为t 秒，则BP =t ，CQ =t ．以P 、Q 、C 为顶点的三角形为等腰三角形，可分三种情况讨论．①若CQ =PC ，如图所示，则PC = CQ =BP =t ．∴有2t =BC=t②若PQ =QC ，如图所示，过点Q 作DQ ⊥BC 交CB 于点D ，则有CD =PD ．由△ABC ∽△QDC ，可得出PD =CDt =，解得t③若PQ =PC ，如图所示，过点P 作PE ⊥AC 交AC 于点E ，则EC =QE=5PC ，∴12t=5（t ），解得t（4）当CQ =PC 时，由（3）知t P 的坐标是（2，1），∴直线OP 的解析式是：y =12x ，因而有12x =12-x 2+32x +2，即x 2-2x -4=0，解得x =1OP 与抛物线的交点坐标为（）和（． 33．（2010湖北省咸宁）已知二次函数2y x bx c =+-的图象与x 轴两交点的坐标分别为（m ，0），（3m -，0）（0m ≠）．（1）证明243c b =；（2）若该函数图象的对称轴为直线1x =，试求二次函数的最小值．【答案】（1）证明：依题意，m ，3m -是一元二次方程20x bx c +-=的两根．根据一元二次方程根与系数的关系，得(3)m m b +-=-，(3)m m c ⨯-=-．∴2b m =，23c m =． ∴224312c b m ==． （2）解：依题意，12b-=，∴2b =-． 由（1）得2233(2)344c b ==⨯-=．∴2223(1)4y x x x =--=--．∴二次函数的最小值为4-．34．（2010湖北恩施自治州） 如图，在平面直角坐标系中，二次函数c bx x y ++=2的图象与x 轴交于A 、B 两点， A 点在原点的左侧，B 点的坐标为（3，0），与y 轴交于C （0，-3）点，点P 是直线BC 下方的抛物线上一动点. （1）求这个二次函数的表达式．（2）连结PO 、PC ，并把△POC 沿CO 翻折，得到四边形POP /C ， 那么是否存在点P ，使四边形POP /C 为菱形？若存在，请求出此时点P 的坐标；若不存在，请说明理由． （3）当点P 运动到什么位置时，四边形 ABPC 的面积最大并求出此时P 点的坐标和四边形ABPC 的最大面积.【答案】解：（1）将B 、C 两点的坐标代入得⎩⎨⎧-==+303c c b解得：⎩⎨⎧-=-=32c b所以二次函数的表达式为：322--=x x y（2）存在点P ，使四边形POP /C 为菱形．设P 点坐标为（x ，322--x x ）， PP /交CO 于E若四边形POP /C 是菱形，则有PC ＝PO ．连结PP / 则PE ⊥CO 于E ，∴OE=EC =23∴y =23-．∴322--x x =23-解得1x =2102+，2x =2102-（不合题意，舍去）∴P 点的坐标为（2102+，23-）…………………………8分 （3）过点P 作y 轴的平行线与BC 交于点Q ，与OB 交于点F ，设P （x ，322--x x ），易得，直线BC 的解析式为3-=x y 则Q 点的坐标为（x ，x －3）.EB QP OE QP OC AB S S S S CPQ BPQ ABC ABPC ⋅+⋅+⋅=++=∆∆∆212121四边形 3)3(2134212⨯+-+⨯⨯=x x =87523232+⎪⎭⎫ ⎝⎛--x当23=x 时，四边形ABPC 的面积最大 此时P 点的坐标为⎪⎭⎫⎝⎛-415,23，四边形ABPC 的 面积875的最大值为． 35．（2010北京）在平面直角坐标系xOy 中，抛物线23454122+-++--=m x x mx m y 与x 轴的交点分别为原点O 和点A ，点B （2，n ）在这条抛物线上． （1）求B 点的坐标；（2）点P 在线段OA 上，从O 点出发向A 点运动，过P 点作x 轴的垂线，与直线OB 交与点E ，延长PE 到点D ，使得ED =PE ，以PD 为斜边，在PD 右侧做等等腰直角三角形PCD （当P 点运动时，C 点、D 点也随之运动）．① 当等腰直角三角形PCD 的顶点C 落在此抛物线上时，求OP 的长；② 若P 点从O 点出发向A 点作匀速运动，速度为每秒1个单位，同时线段OA 上另一个点Q 从A 点出发向O 点作匀速运动，速度为每秒2个单位（当Q 点到达O 点时停止运动，P 点也同时停止运动）．过Q 点做x 轴的垂线，与直线AB 交与点F ，延长QF 到点M ，使得FM =QF ，以QM 为斜边，在QM 的左侧作等腰直角三角形QMN （当Q点运动时，M 点、N 点也随之运动）．若P 点运动到t 秒时，两个等腰直角三角形分别有一条边恰好落在同一条直线上，求此刻t 的值．【答案】解：（1）∵抛物线23454122+-++--=m m x mx m y 经过原点， ∴m 2—3m +2=0. 解的m 1=1，m 2=2. 由题意知m ≠1. ∴m =2，∴抛物线的解析式为x x y 25412+-= ∵点B （2，n ）在抛物线x x y 25412+-=，n=4.∴B 点的坐标为（2，4）（2）①设直线OB 的解析式为y =k 1x 求得直线OB 的解析式y =2x ∵A 点是抛物线与x 轴的一个交点， 可求得A 点的坐标为（10，0），设P 点的坐标为（a ，0），则E 点的坐标为（a ，2a ）． 根据题意做等腰直角三角形PCD ，如图1.可求得点C 的坐标为（3a ，2a ）， 有C 点在抛物线上，得2a =－41x （3a ）2+25x 3a . 即49a 2— 211a =0解得 a 1=922，a 2=0（舍去） ∴OP =922 ②依题意作等腰直角三角形QMN . 设直线AB 的解析式y =k 2x +b由点A (10 ，0)，点B （2，4），求得直线AB 的解析式为y =－21x +5 当P 点运动到t 秒时，两个等腰直角三角形分别有一条边恰好落在同一条直线上，有以下三种情况：第一种情况：CD 与NQ 在同一条直线上，如图2所示，可证△DPQ 为等腰直角三角形．此时QP 、OP 、AQ 的长可依次表示为t 、4t 、 2t 个单位． ∴PQ = DP = 4t ∴t +4t +2t =10 ∴t=710第二种情况：PC 与MN 在同一条直线上，如图3所示．可证△PQM 为等腰直角三角形．此时OP 、AQ 的长依次表示为t 、2t 个单位， ∴OQ = 10 － 2t ∵F 点在直线AB 上 ∴FQ =t ∵MQ =2t ∴PQ =MQ =CQ =2t ∴t +2t +2t =10 ∴t =2.第三种情况：点P 、Q 重合时，PD 、QM 在同一条直线上，如图4所示，此时OP 、AQ 的长依次表示为t 、2t 个单位．∴t +2t=10 ∴t =310 综上，符合题意的值分别为710，2，310． 36．（2010云南红河哈尼族彝族自治州）二次函数2x y =的图像如图8所示，请将此图像向右平移1个单位，再向下平移2个单位.（1）画出经过两次平移后所得到的图像，并写出函数的解析式.（2）求经过两次平移后的图像与x 轴的交点坐标，指出当x 满足什么条件时，函数值大于0？【答案】解：画图如图所示：依题意得：2)1(2--=x y =2122-+-x x =122--x x∴平移后图像的解析式为：122--x x （2）当y=0时，122--x x =0 2)1(2=-x 21±=-x 212121+=-=x x ，∴平移后的图像与x 轴交与两点，坐标分别为（21-，0）和（21+，0） 由图可知，当x<21-或x>21+时，二次函数2)1(2--=x y 的函数值大于0. 37．（2010云南楚雄）已知：如图，抛物线2y ax bx c =++与x 轴相交于两点A (1，0)，B (3，0).与y 轴相较于点C （0，3）．（1）求抛物线的函数关系式； （2）若点D （7,2m ）是抛物线2y ax bx c =++上一点，请求出m 的值，并求处此时△ABD 的面积．【答案】解：（1）由题意可知09303a b c a b c c ++=⎧⎪++=⎨⎪=⎩ 解得143a b c =⎧⎪=-⎨⎪=⎩所以抛物线的函数关系式为243y x x =-+． （2）把D （7,2m ）代人函数解析式243y x x =-+中，得2775()43224m =-⨯+=．所以155(31)244ABDS ∆=⨯-⨯=． 38．（2010湖北随州）已知抛物线2(0)y ax bx c a =++≠顶点为C （1，1）且过原点O.过抛物线上一点P （x ，y ）向直线54y =作垂线，垂足为M ，连FM （如图）. （1）求字母a ，b ，c 的值；（2）在直线x ＝1上有一点3(1,)4F ，求以PM 为底边的等腰三角形PFM 的P 点的坐标，并证明此时△PFM 为正三角形；（3）对抛物线上任意一点P ，是否总存在一点N （1，t ），使PM ＝PN 恒成立，若存在请求出t 值，若不存在请说明理由.【答案】（1）a ＝－1，b ＝2，c ＝0（2）过P 作直线x=1的垂线，可求P 的纵坐标为14，横坐标为1.此时，MP ＝MF ＝PF ＝1，故△MPF 为正三角形. （3）不存在.因为当t ＜54，x ＜1时，PM 与PN 不可能相等，同理，当t ＞54，x ＞1时，PM 与PN 不可能相等.39．（2010河南）在平面直角坐标系中，已知抛物线经过A(4，0)，B(0，一4)，C(2，0)三点.(1)求抛物线的解析式；(2)若点M 为第三象限内抛物线上一动点，点M 的横坐标为m ，△AMB 的面积为S.求S 关于m 的函数关系式，并求出S 的最大值；(3)若点P 是抛物线上的动点，点Q 是直线y=－x 上的动点，判断有几个位置能使以点P 、Q 、B 、0为顶点的四边形为平行四边形，直接写出相应的点Q 的坐标.【答案】（1）设抛物线的解析式为y =ax 2+bx +c (a ≠0)，则有1640,4,420.a b c c a b c -+=⎧⎪=-⎨⎪++=⎩解得1,21,4.a b c ⎧=⎪⎪=⎨⎪=-⎪⎩∴抛物线的解析式y =12x 2+x ﹣4（2）过点M 作MD ⊥x 轴于点D .设M 点的坐标为（m ，n ）. 则AD =m +4，MD =﹣n ，n =12m 2＋m －4 . ∴S = S △AMD +S 梯形DMBO －S △ABO =12( m +4) (﹣n )＋12(﹣n ＋4) (﹣m ) －12×4×4 = ﹣2n -2m -8 = ﹣2(12m 2＋m －4) -2m -8= ﹣m 2-4m (－4< m < 0)∴S 最大值 = 4（3）满足题意的Q 点的坐标有四个，分别是：（-4 ，4 ），（4 ，-4），（-2+2－，（-2－2＋40．（2010四川乐山）如图(13.1)，抛物线y ＝x2+bx+c 与x 轴交于A ，B 两点，与y 轴交于点C(0，2)，连接AC ，若tan ∠OAC ＝2． (1)求抛物线对应的二次函数的解析式；(2)在抛物线的对称轴l 上是否存在点P ，使∠APC ＝90°，若存在，求出点P 的坐标；若不存在，请说明理由；(3)如图(13.2)所示，连接BC ，M 是线段BC 上(不与B 、C 重合)的一个动点，过点M 作直线l ′∥l ，交抛物线于点N ，连接CN 、BN ，设点M 的横坐标为t ．当t 为何值时，△BCN 的面积最大？最大面积为多少？【答案】解：（1）∵抛物线y=x 2＋bx ＋c 过点C(0,2). ∴x=2又∵tan ∠OAC=OCOA=2, ∴OA=1,即A(1,0). 又∵点A 在抛物线y=x 2＋bx ＋2上. ∴0=12＋b ×1＋2,b=－3 ∴抛物线对应的二次函数的解析式为y=x 2－3x ＋2 （2）存在过点C 作对称轴l 的垂线,垂足为D,如图所示, ∴x=－332212b a -=-=⨯.∴AE=OE-OA=32-1=12,∵∠APC=90°,∴tan ∠PAE= tan ∠CPD ∴PE CDEA DP=,即12PE 322PE =-，解得PE=12或PE=32， ∴点P 的坐标为（32，12）或（32，32）。

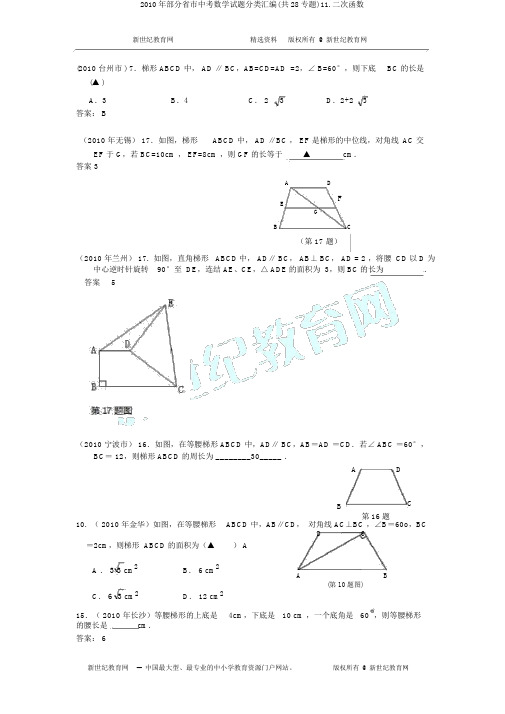
新世纪教育网精选资料版权所有@新世纪教育网(2010 台州市 ) 7．梯形 ABCD 中， AD ∥ BC，AB=CD=AD =2，∠ B=60°，则下底BC 的长是(▲ )A．3B．4C． 2 3D．2+23答案： B（2010 年无锡） 17．如图，梯形ABCD 中， AD ∥BC ， EF 是梯形的中位线，对角线AC 交EF 于 G，若 BC=10cm ， EF=8cm ，则 GF 的长等于▲cm．答案 3A DFEGB C（第 17 题）（2010 年兰州） 17. 如图，直角梯形 ABCD中， AD∥ BC， AB⊥ BC， AD = 2 ，将腰 CD以 D 为中心逆时针旋转90°至 DE，连结 AE、CE，△ ADE的面积为 3，则 BC的长为．答案5（2010 宁波市） 16．如图，在等腰梯形 ABCD 中，AD∥ BC，AB＝AD ＝CD．若∠ ABC ＝60°，BC＝ 12，则梯形 ABCD 的周长为 ________30_____ ．A DB C第16题10. （ 2010 年金华）如图，在等腰梯形ABCD 中，AB∥CD，对角线 AC⊥BC ，∠B＝60o，BCD C＝2cm，则梯形 ABCD 的面积为（▲） AA ．3 3 cm2B． 6 cm2A B(第 10题图) C．6 3 cm2D． 12 cm215．（ 2010 年长沙）等腰梯形的上底是4cm，下底是10 cm ，一个底角是60 ，则等腰梯形的腰长是cm．答案： 6（2010 年眉山） 18．如，已知梯形 ABCD 中， AD∥ BC，∠ B=30°，∠ C=60°，AD=4 ， AB= 3 3，下底BC 的__________．A D答案： 1030°60°（2010 陕西省）16、如图，在梯形ABCD 中，B C DC∥AB ，∠ A+ ∠B=90°若 AB=10 ，AD=4,DC=5 ，则梯形 ABCD 的面积为181.（ 2010 黄）如，在等腰梯形ABCD 中， AC ⊥ BD ，AC ＝26cm，等腰梯形ABCD 的面 _____cm .181．（ 2010 昆明）已知：如，在梯形ABCD 中， AD ∥BC，∠DCB = 90 °， E 是 AD 的中点，点 P 是 BC 上的点（不与点 B重合）， EP 与 BD 订交于点 O.（1）当 P 点在 BC 上运，求：△ BOP∽△ DOE；（2）（ 1）中的相像比k，若 AD ︰ BC = 2 ︰ 3. 研究：当形ABPE是什么四形？①当k = 1，是是；③当 k = 3，是k以下三种状况，四；②当 k = 2，.并明 k = 2的.．．．A E D OBP C解：（ 1）明：∵ AD ∥ BC∴∠ OBP = ∠ODE⋯⋯⋯⋯⋯1分在△ BOP 和△ DOE 中∠OBP = ∠ ODE∠ BOP = ∠ DOE⋯⋯⋯⋯⋯⋯⋯2分∴△ BOP∽△ DOE (有两个角相等的两三角形相像 )⋯⋯⋯⋯⋯3分（ 2）①平行四形⋯⋯⋯⋯⋯⋯⋯4分②直角梯形⋯⋯⋯⋯⋯⋯⋯5分③ 等腰梯形分明：∵ k = 2 ，BPDE⋯⋯⋯⋯⋯⋯⋯6 2∴BP=2DE=AD又∵AD︰BC=2︰ 3BC= 3 AD 2PC=BC - BP=31 AD -AD= AD=ED 22ED ∥ PC , ∴四形 PCDE是平行四形∵∠ DCB = 90°∴四形 PCDE 是矩形⋯⋯⋯⋯⋯⋯⋯7分∴ ∠ EPB = 90°⋯⋯⋯⋯⋯⋯⋯8分又∵在直角梯形ABCD中AD ∥ BC,AB 与DC 不平行∴ AE∥ BP,AB 与 EP不平行四形 ABPE 是直角梯形⋯⋯⋯⋯⋯⋯⋯⋯⋯9分（本其余法参照此准分）（2010 河北省） 25．（本小题满分 12 分）如图 16，在直角梯形 ABCD 中， AD ∥BC ， B 90 ， AD = 6， BC = 8， AB 33 ，点 M 是 BC 的中点．点 P 从点 M 出发沿 MB 以每秒 1 个单位长的速度向点 B 匀速运动，到 达点 B 后马上以原速度沿 BM 返回；点 Q 从点 M 出发以每秒 1 个单位长的速度在射线 MC上匀速运动．在点 P ， Q 的运动过程中，以PQ 为边作等边三角形 EPQ ，使它与梯形 ABCD 在射线 BC 的同侧．点 P ， Q 同时出发，当点 P 返回到点 M 时停止运动，点 Q 也随之停止．设点 P ，Q 运动的时间是t 秒 (t ＞ 0)．（ 1）设 PQ 的长为 y ，在点 P 从点 M 向点 B 运动的过程中，写出y 与 t 之间的函数关系式（不用写 t 的取值范围） ．（ 2）当 BP = 1 时，求△ EPQ 与梯形 ABCD 重叠部分的面积．（ 3）跟着时间 t 的变化，线段 AD 会有一部分被△ EPQ 覆盖，被覆盖线段的长度在某个时辰会达到最大值，请回答：该最大值可否连续一个时段？若能，直接．．写出 t的取值范围；若不可以，请说明原因．ADEBP M QC图 16A D解：（ 1） y = 2t ；（ 2）当 BP = 1 时，有两种情况：BM C（备用图）①如图 6，若点 P 从点 M 向点 B 运动，有 MB =1BC=4，MP = MQ =3，2A∴PQ = 6．连结 EM ，ED∵△ EPQ 是等边三角形， ∴ EM ⊥ PQ ．∴ EM 3 3 ． ∵AB= 3 3，∴点 E 在 AD 上．B PM Q C图 6∴△ EPQ 与梯形 ABCD 重叠部分就是△ EPQ ，其面积为93．②若点 P 从点 B 向点 M 运动，由题意得t 5 ．PQ=BM+MQ BP = 8，PC = 7．设 PE 与 AD 交于点 F ，QE 与 AD 或 AD 的E 延伸线交于点G ，过点 P 作 PH ⊥AD 于点 H ，则AHFG DHP = 3 3 ， AH = 1．在 Rt△HPF 中，∠ HPF = 30°，∴HF = 3，PF = 6．∴ FG = FE = 2．又∵ FD = 2，∴点 G 与点 D 重合，如图 7．此时△ EPQ 与梯形 ABCD的重叠部分就是梯形FPCG ，其面积为273 ．2（ 3）能． 4≤ t≤ 5．（2010 ·浙江温州）10．用若干根同样的火柴棒首尾按序相接围成一个梯形( 供给的火柴棒所有用完 ) ，以下根数的火柴棒不可以围成梯形的是(B)．A．5 B．6C．7D．81．（2010，安徽芜湖）在等腰梯形ABCD 中， AD ∥ BC, 对角线 AC ⊥BD 于点 O,AE ⊥ BC,DF⊥BC, 垂足分别为E,F,AD=4,BC=8, 则 AE+EF= （）A．9B．10C．11D．20【答案】 B（2010 ·浙江湖州） 20．（本小题8 分）如图，已知在梯形ABCD 中， DC ∥AB ，AD＝ BC，BD 均分∠ ABC，∠ A＝ 60°．（1）求∠ ABD 的度数；D C （2）若 AD＝2，求对角线 BD 的长．A B第20题。

28．（2010广东中山）如图（1），（2）所示，矩形ABCD 的边长AB=6，BC=4，点F 在DC 上，DF=2．动点M 、N 分别从点D 、B 同时出发，沿射线DA 、线段BA 向点A 的方向运动（点M 可运动到DA 的延长线上），当动点N 运动到点A 时，M 、N 两点同时停止运动．连接FM 、MN 、FN ，当F 、N 、M 不在同一直线时，可得ΔFMN ，过ΔFMN 三边的中点作ΔPQW ．设动点M 、N 的速度都是1个单位/秒，M 、N 运动的时间为x 秒．试解答下列问题：（1）说明ΔFMN ∽ΔQWP ；（2）设0≤x ≤4（即M 从D 到A 运动的时间段）．试问x 为何值时，ΔPQW 为直角三角形？当x 在何范围时，ΔPQW 不为直角三角形？（3）问当x 为何值时，线段MN 最短？求此时MN 的值．．【答案】解：（1）由题意可知P 、W 、Q 分别是ΔFMN 三边的中点，∴PW 是ΔFMN 的中位线，即PW ∥MN∴ΔFMN ∽ΔQWP（2）由题意可得 DM=BN=x ，AN=6-x ，AM=4-x ，由勾股定理分别得 2FM =24x +，2MN =2)4(x -+2)6(x -2FN =2)4(x -+16①当2MN =2FM +2FN 时，2)4(x -+2)6(x -=24x ++2)4(x -+16解得 34=x②当2FN =2FM +2MN 时，2)4(x -+16=24x ++2)4(x -+2)6(x -此方程无实数根③2FM =2MN +2FN 时，24x +=2)4(x -+2)6(x -+2)4(x -+16解得 101=x （不合题意，舍去），42=x综上，当34=x 或4=x 时，ΔPQW 为直角三角形；当0≤x ＜34或34＜x ＜4时，ΔPQW 不为直角三角形（3）①当0≤x ≤4，即M 从D 到A 运动时，只有当x=4时，MN 的值最小，等于2；②当4＜x ≤6时，2MN =2AM +2AN =2)4(-x +2)6(x -=2)5(22+-x当x=5时，2MN 取得最小值2，∴当x=5时，线段MN 最短，MN=2．29．（2010湖南常德）如图9, 已知抛物线212y x bx c =++与x 轴交于A (－4，0) 和B (1，0)两点，与y 轴交于C 点．（1）求此抛物线的解析式；（2）设E 是线段AB 上的动点，作EF //AC 交BC 于F ，连接CE ，当△CEF 的面积是△BEF 面积的2倍时，求E 点的坐标;（3）若P 为抛物线上A 、C 两点间的一个动点，过P 作y 轴的平行线，交AC 于Q ，当P 点运动到什么位置时，线段PQ 的值最大，并求此时P 点的坐标．【答案】解：（1）由二次函数212y x bx c =++与x 轴交于(4,0)A -、(1,0)B 两点可得：221(4)4021102b c b c ⎧--+=⎪⎪⎨⎪⋅++=⎪⎩，． 解得： 322b c ⎧=⎪⎨⎪=-⎩，．故所求二次函数的解析式为213222y x x =+-．（2）∵S △CEF =2 S △BEF , ∴1,2BF CF =1.3BF BC =∵EF //AC , ∴B ,EF BAC BFE BCA ∠=∠∠=∠ ,∴△BEF ～△BAC ,∴1,3BE BF BA BC ==得5,3BE =故E 点的坐标为(23-,0).（3）解法一：由抛物线与y 轴的交点为C ，则C 点的坐标为（0，－2）．若设直线AC 的解析式为y kx b =+，则有20,04b k b -=+⎧⎨=-+⎩． 解得：1,22k b ⎧=-⎪⎨⎪=-⎩．故直线AC 的解析式为122y x =-－．若设P 点的坐标为213,222a a a ⎛⎫+- ⎪⎝⎭，又Q 点是过点P 所作y 轴的平行线与直线AC 的交点，则Q 点的坐标为（1,2)2a a --．则有：2131[(2)](2)222PQ a a a =-+----＝2122a a--＝()21222a -++ 即当2a =-时，线段PQ 取大值，此时P 点的坐标为（－2，－3）解法二：延长PQ 交x 轴于D 点，则PD AB ⊥．要使线段PQ 最长，则只须△APC 的面积取大值时即可.设P 点坐标为（),00y x ，则有:ACO DPCO S APC ADP S S S =+-V V V 梯形xyO BC A图9＝111()222AD PD PD OC OD OA OC ⋅++⋅-⋅＝()()000001112242222x y y y x --+-+⋅--⨯⨯＝0024y x ---＝20001322422x x x ⎛⎫-+---⎪⎝⎭＝2004xx -- ＝－()22024x ++即02x =-时，△APC 的面积取大值，此时线段PQ 最长，则P 点坐标为（－2，－3）30 ．（2010湖南郴州）如图（1），抛物线42y x x =+-与y 轴交于点A ，E （0，b ）为y 轴上一动点，过点E 的直线y x b =+与抛物线交于点B 、C .（1）求点A 的坐标；（2)当b =0时（如图（2）），ABE V 与ACE V 的面积大小关系如何？当4b >-时，上述关系还成立吗，为什么？ （3）是否存在这样的b ，使得BOC V 是以BC 为斜边的直角三角形，若存在，求出b ；若不存在，说明理由.【答案】（1）将x =0，代入抛物线解析式，得点A 的坐标为（0，－4）（2）当b ＝0时，直线为y x =，由24y x y x x =⎧⎨=+-⎩解得1122x y =⎧⎨=⎩，2222x y =-⎧⎨=-⎩所以B 、C 的坐标分别为（－2，－2），（2，2）14242ABE S =⨯⨯=V ，14242ACE S =⨯⨯=V所以ABE ACE S S =V V （利用同底等高说明面积相等亦可）当4b >-时，仍有ABE ACE S S =V V 成立. 理由如下由24y x b y x x =+⎧⎨=+-⎩，解得11x y b ⎧=⎪⎨=⎪⎩，22x y b⎧=⎪⎨=⎪⎩所以B 、C 的坐标分别为（－4b +，－4b ++b ），（4b +，4b ++b ），作BF y ⊥轴，CG y ⊥轴，垂足分别为F 、G ，则4BF CG b ==+，而ABE V 和ACE V 是同底的两个三角形，所以ABE ACE S S =V V .（3）存在这样的b .因为90BF CG,BEF CEG,BFE CGE =∠=∠∠=∠=︒所以BEF CEG≅V V所以BE CE =，即E 为BC 的中点所以当OE =CE 时，OBC V 为直角三角形因为44GE b b b b GC =++-=+=所以 24CE b =⋅+，而OE b=所以24b b ⋅+=，解得124,2b b ==-，所以当b ＝4或－2时，ΔOBC 为直角三角形.31．（2010湖南怀化）图9是二次函数k m x y ++=2)(的图象，其顶点坐标为M(1,-4).（1）求出图象与x 轴的交点A,B 的坐标；（2）在二次函数的图象上是否存在点P ，使MAB PABS S ∆∆=45,若存在，求出P 点的坐标；若不存在，请说明理由；（3）将二次函数的图象在x 轴下方的部分沿x 轴翻折，图象的其余部分保持不变，得到一个新的图象，请你结合这个新的图象回答：当直线)1(<+=b b x y 与此图象有两个公共点时，b 的取值范围.【答案】解;(1) 因为M(1,-4) 是二次函数k m x y ++=2)(的顶点坐标，所以324)1(22--=--=x x x y令,0322=--x x 解之得3,121=-=x x .∴A ，B 两点的坐标分别为A （-1，0），B （3,0）(2) 在二次函数的图象上存在点P ，使MAB PAB S S ∆∆=45设),,(y x p 则y y AB S PAB 221=⨯=∆，又8421=-⨯=∆AB S MAB ,图9∴.5,8452±=⨯=y y 即∵二次函数的最小值为-4，∴5=y .当5=y 时，4,2=-=x x 或.故P 点坐标为（-2，5）或（4，5）……………7分（3）如图1，当直线)1(<+=b b x y 经过A 点时，可得.1=b ……………8分当直线)1(<+=b b x y 经过B 点时，可得.3-=b由图可知符合题意的b 的取值范围为13<<-b32．（2010湖北鄂州）如图，在直角坐标系中，A （-1，0），B （0，2），一动点P 沿过B 点且垂直于AB 的射线BM 运动，P 点的运动速度为每秒1个单位长度，射线BM 与x 轴交与点C ．（1）求点C 的坐标．（2）求过点A 、B 、C 三点的抛物线的解析式．（3）若P 点开始运动时，Q 点也同时从C 出发，以P 点相同的速度沿x 轴负方向向点A 运动，t 秒后，以P 、Q 、C 为顶点的三角形为等腰三角形．（点P 到点C 时停止运动，点Q 也同时停止运动）求t 的值． （4）在（2）（3）的条件下，当CQ =CP 时，求直线OP 与抛物线的交点坐标．【答案】（1）点C 的坐标是（4，0）； （2）设过点A 、B 、C 三点的抛物线的解析式为y =ax 2+bx +c （a ≠0），将点A 、B 、C 三点的坐标代入得：020164a b c c a b c =-+⎧⎪=⎨⎪=++⎩解得12322a b c ⎧=-⎪⎪⎪=⎨⎪=⎪⎪⎩，∴抛物线的解析式是：y = 12-x 2+32x +2．（3）设P 、Q 的运动时间为t 秒，则BP =t ，CQ =t ．以P 、Q 、C 为顶点的三角形为等腰三角形，可分三种情况讨论．①若CQ =PC ，如图所示，则PC = CQ =BP =t ．∴有2t =BC =25，∴t =5．②若PQ =QC ，如图所示，过点Q 作DQ ⊥BC 交CB 于点D ，则有CD =PD ．由△ABC ∽△QDC ，可得出PD =CD =25t ，∴4525t t =-，解得t =40105-．③若PQ =PC ，如图所示，过点P 作PE ⊥AC 交AC 于点E ，则EC =QE =25PC ，∴12t =25（25-t ），解得t =32540-．（4）当CQ =PC 时，由（3）知t =5，∴点P 的坐标是（2，1），∴直线OP 的解析式是：y =12x ，图1因而有12x =12-x 2+32x +2，即x 2-2x -4=0，解得x =1±5，∴直线OP 与抛物线的交点坐标为（1+5，15+）和（1-5，15-）．33．（2010湖北省咸宁）已知二次函数2y x bx c =+-的图象与x 轴两交点的坐标分别为（m ，0），（3m -，0）（0m ≠）．（1）证明243c b =；（2）若该函数图象的对称轴为直线1x =，试求二次函数的最小值．【答案】（1）证明：依题意，m ，3m -是一元二次方程20x bx c +-=的两根．根据一元二次方程根与系数的关系，得(3)m m b +-=-，(3)m m c ⨯-=-．∴2b m =，23c m =．∴224312c b m ==．（2）解：依题意，12b-=，∴2b =-．由（1）得2233(2)344c b ==⨯-=．∴2223(1)4y x x x =--=--．∴二次函数的最小值为4-．34．（2010湖北恩施自治州） 如图，在平面直角坐标系中，二次函数c bx x y ++=2的图象与x 轴交于A 、B 两点， A 点在原点的左侧，B 点的坐标为（3，0），与y 轴交于C （0，-3）点，点P 是直线BC 下方的抛物线上一动点. （1）求这个二次函数的表达式．（2）连结PO 、PC ，并把△POC 沿CO 翻折，得到四边形POP /C ， 那么是否存在点P ，使四边形POP /C 为菱形？若存在，请求出此时点P 的坐标；若不存在，请说明理由．（3）当点P 运动到什么位置时，四边形 ABPC 的面积最大并求出此时P 点的坐标和四边形ABPC 的最大面积.【答案】解：（1）将B 、C 两点的坐标代入得⎩⎨⎧-==+33c c b解得：⎩⎨⎧-=-=32c b所以二次函数的表达式为：322--=x x y（2）存在点P ，使四边形POP /C 为菱形．设P 点坐标为（x ，322--x x ），PP /交CO 于E若四边形POP /C 是菱形，则有PC ＝PO ．连结PP /则PE ⊥CO 于E ，∴OE=EC =23∴y =23-．∴322--x x =23-解得1x =2102+，2x =2102-（不合题意，舍去）∴P 点的坐标为（2102+，23-）…………………………8分（3）过点P 作y 轴的平行线与BC 交于点Q ，与OB 交于点F ，设P （x ，322--x x ），易得，直线BC 的解析式为3-=x y则Q 点的坐标为（x ，x －3）.EB QP OE QP OC AB S S S S CPQ BPQ ABC ABPC ⋅+⋅+⋅=++=∆∆∆212121四边形 3)3(2134212⨯+-+⨯⨯=x x =87523232+⎪⎭⎫ ⎝⎛--x当23=x 时，四边形ABPC 的面积最大此时P 点的坐标为⎪⎭⎫⎝⎛-415,23，四边形ABPC 的面积875的最大值为．35．（2010北京）在平面直角坐标系xOy 中，抛物线23454122+-++--=m x x mx m y 与x 轴的交点分别为原点O 和点A ，点B （2，n ）在这条抛物线上．（1）求B 点的坐标；（2）点P 在线段OA 上，从O 点出发向A 点运动，过P 点作x 轴的垂线，与直线OB 交与点E ，延长PE 到点D ，使得ED =PE ，以PD 为斜边，在PD 右侧做等等腰直角三角形PCD （当P 点运动时，C 点、D 点也随之运动）．① 当等腰直角三角形PCD 的顶点C 落在此抛物线上时，求OP 的长；② 若P 点从O 点出发向A 点作匀速运动，速度为每秒1个单位，同时线段OA 上另一个点Q 从A 点出发向O 点作匀速运动，速度为每秒2个单位（当Q 点到达O 点时停止运动，P 点也同时停止运动）．过Q 点做x 轴的垂线，与直线AB 交与点F ，延长QF 到点M ，使得FM =QF ，以QM 为斜边，在QM 的左侧作等腰直角三角形QMN （当Q 点运动时，M 点、N点也随之运动）．若P 点运动到t 秒时，两个等腰直角三角形分别有一条边恰好落在同一条直线上，求此刻t 的值．【答案】解：（1）∵抛物线23454122+-++--=m m x m x m y 经过原点，∴m 2—3m +2=0.解的m 1=1，m 2=2. 由题意知m ≠1. ∴m =2，∴抛物线的解析式为xx y 25412+-=∵点B （2，n ）在抛物线x x y 25412+-=，n=4.∴B 点的坐标为（2，4）（2）①设直线OB 的解析式为y =k 1x求得直线OB 的解析式y =2x∵A 点是抛物线与x 轴的一个交点，可求得A 点的坐标为（10，0），设P 点的坐标为（a ，0），则E 点的坐标为（a ，2a ）．根据题意做等腰直角三角形PCD ，如图1.可求得点C 的坐标为（3a ，2a ），有C 点在抛物线上，得2a =－41x （3a ）2+25x 3a .即49a 2— 211a =0解得 a 1=922，a 2=0（舍去）∴OP =922②依题意作等腰直角三角形QMN .设直线AB 的解析式y =k 2x +b由点A (10 ，0)，点B （2，4），求得直线AB 的解析式为y =－21x +5当P 点运动到t 秒时，两个等腰直角三角形分别有一条边恰好落在同一条直线上，有以下三种情况：第一种情况：CD 与NQ 在同一条直线上，如图2所示，－1 yx O（第24题） 1234 －2 －4 －33 －1－2 －3 －4 4 1 2可证△DPQ为等腰直角三角形．此时QP、OP、AQ的长可依次表示为t、4t、 2t个单位．∴PQ = DP = 4t∴t+4t+2t=10∴t=710第二种情况：PC与MN在同一条直线上，如图3所示．可证△PQM为等腰直角三角形．此时OP、AQ的长依次表示为t、2t个单位，∴OQ = 10 － 2t∵F点在直线AB上∴FQ=t∵MQ=2t∴PQ=MQ=CQ=2t∴t+2t+2t=10∴t=2.第三种情况：点P、Q重合时，PD、QM在同一条直线上，如图4所示，此时OP、AQ的长依次表示为t、2t个单位．∴t+2t=10∴t=310综上，符合题意的值分别为710，2，310．36．（2010云南红河哈尼族彝族自治州）二次函数2xy=的图像如图8所示，请将此图像向右平移1个单位，再向下平移2个单位.（1）画出经过两次平移后所得到的图像，并写出函数的解析式.（2）求经过两次平移后的图像与x轴的交点坐标，指出当x满足什么条件时，函数值大于0？【答案】解：画图如图所示：依题意得：2)1(2--=xy=2122-+-xx=122--xx∴平移后图像的解析式为：122--xx（2）当y=0时，122--x x =02)1(2=-x 21±=-x 212121+=-=x x ，∴平移后的图像与x 轴交与两点，坐标分别为（21-，0）和（21+，0）由图可知，当x<21-或x>21+时，二次函数2)1(2--=x y 的函数值大于0.37．（2010云南楚雄）已知：如图，抛物线2y ax bx c =++与x 轴相交于两点A (1，0)，B (3，0).与y 轴相较于点C （0，3）．（1）求抛物线的函数关系式； （2）若点D （7,2m ）是抛物线2y ax bx c =++上一点，请求出m 的值，并求处此时△ABD 的面积．【答案】解：（1）由题意可知09303a b c a b c c ++=⎧⎪++=⎨⎪=⎩解得143a b c =⎧⎪=-⎨⎪=⎩所以抛物线的函数关系式为243y x x =-+．（2）把D （7,2m ）代人函数解析式243y x x =-+中，得2775()43224m =-⨯+=．所以155(31)244ABD S ∆=⨯-⨯=．38．（2010湖北随州）已知抛物线2(0)y ax bx c a =++≠顶点为C （1，1）且过原点O.过抛物线上一点P （x ，y ）向直线54y =作垂线，垂足为M ，连FM （如图）.（1）求字母a ，b ，c 的值；（2）在直线x ＝1上有一点3(1,)4F ，求以PM 为底边的等腰三角形PFM 的P 点的坐标，并证明此时△PFM 为正三角形； （3）对抛物线上任意一点P ，是否总存在一点N （1，t ），使PM ＝PN 恒成立，若存在请求出t值，若不存在请说明理由.【答案】（1）a ＝－1，b ＝2，c ＝031241234O1-2-1-2-xy（2）过P 作直线x=1的垂线，可求P 的纵坐标为14，横坐标为1132+.此时，MP ＝MF ＝PF ＝1，故△MPF 为正三角形.（3）不存在.因为当t ＜54，x ＜1时，PM 与PN 不可能相等，同理，当t ＞54，x ＞1时，PM 与PN 不可能相等.39．（2010河南）在平面直角坐标系中，已知抛物线经过A(4，0)，B(0，一4)，C(2，0)三点.(1)求抛物线的解析式；(2)若点M 为第三象限内抛物线上一动点，点M 的横坐标为m ，△AMB 的面积为S.求S 关于m 的函数关系式，并求出S 的最大值； (3)若点P 是抛物线上的动点，点Q 是直线y=－x 上的动点，判断有几个位置能使以点P 、Q 、B 、0为顶点的四边形为平行四边形，直接写出相应的点Q 的坐标.【答案】（1）设抛物线的解析式为y =ax 2+bx +c (a ≠0)，则有1640,4,420.a b c c a b c -+=⎧⎪=-⎨⎪++=⎩解得1,21,4.a b c ⎧=⎪⎪=⎨⎪=-⎪⎩∴抛物线的解析式y =12x 2+x ﹣4（2）过点M 作MD ⊥x 轴于点D .设M 点的坐标为（m ，n ）.则AD =m +4，MD =﹣n ，n =12m 2＋m －4 .∴S = S △AMD +S 梯形DMBO －S △ABO=12( m +4) (﹣n )＋12(﹣n ＋4) (﹣m ) －12×4×4= ﹣2n -2m -8= ﹣2(12m 2＋m －4) -2m -8= ﹣m 2-4m (－4< m < 0)∴S 最大值 = 4（3）满足题意的Q 点的坐标有四个，分别是：（-4 ，4 ），（4 ，-4），（-2+252－5，（-2－52＋2540．（2010四川乐山）如图(13.1)，抛物线y ＝x2+bx+c 与x 轴交于A ，B 两点，与y 轴交于点C(0，2)，连接AC ，若tan ∠OAC ＝2． (1)求抛物线对应的二次函数的解析式； (2)在抛物线的对称轴l 上是否存在点P ，使∠APC ＝90°，若存在，求出点P 的坐标；若不存在，请说明理由；(3)如图(13.2)所示，连接BC ，M 是线段BC 上(不与B 、C 重合)的一个动点，过点M 作直线l ′∥l ，交抛物线于点N ，连接CN 、BN ，设点M 的横坐标为t ．当t 为何值时，△BCN 的面积最大？最大面积为多少？【答案】解：（1）∵抛物线y=x2＋bx＋c过点C(0,2). ∴x=2又∵tan∠OAC=OCOA=2, ∴OA=1,即A(1,0).又∵点A在抛物线y=x2＋bx＋2上. ∴0=12＋b×1＋2,b=－3∴抛物线对应的二次函数的解析式为y=x2－3x＋2（2）存在过点C作对称轴l的垂线,垂足为D,如图所示,∴x=－332212ba-=-=⨯.∴AE=OE-OA=32-1=12,∵∠APC=90°,∴tan∠PAE= tan∠CPD∴PE CDEA DP=,即12PE322PE=-，解得PE=12或PE=32，∴点P的坐标为（32，12）或（32，32）。

一、二次函数 真题与模拟题分类汇编（难题易错题）1．如图，直线AB 和抛物线的交点是A （0，﹣3），B （5，9），已知抛物线的顶点D 的横坐标是2．（1）求抛物线的解析式及顶点坐标；（2）在x 轴上是否存在一点C ，与A ，B 组成等腰三角形？若存在，求出点C 的坐标，若不在，请说明理由；（3）在直线AB 的下方抛物线上找一点P ，连接PA ，PB 使得△PAB 的面积最大，并求出这个最大值．【答案】（1）21248355y x x =--，顶点D （2，635-）；（2）C （10±0）或（5222±0）或（9710，0）；（3）752【解析】 【分析】（1）抛物线的顶点D 的横坐标是2，则x 2ba=-=2，抛物线过A （0，﹣3），则：函数的表达式为：y =ax 2+bx ﹣3，把B 点坐标代入函数表达式，即可求解； （2）分AB =AC 、AB =BC 、AC =BC ，三种情况求解即可；（3）由S △PAB 12=•PH •x B ，即可求解． 【详解】（1）抛物线的顶点D 的横坐标是2，则x 2ba=-=2①，抛物线过A （0，﹣3），则：函数的表达式为：y =ax 2+bx ﹣3，把B 点坐标代入上式得：9=25a +5b ﹣3②，联立①、②解得：a 125=，b 485=-，c =﹣3，∴抛物线的解析式为：y 125=x 2485-x ﹣3．当x=2时，y635=-，即顶点D的坐标为（2，635-）；（2）A（0，﹣3），B（5，9），则AB=13，设点C坐标（m，0），分三种情况讨论：①当AB=AC时，则：（m）2+（﹣3）2=132，解得：m=±410，即点C坐标为：（410，0）或（﹣410，0）；②当AB=BC时，则：（5﹣m）2+92=132，解得：m=5222±，即：点C坐标为（5222+，0）或（5﹣222，0）；③当AC=BC时，则：5﹣m）2+92=（m）2+（﹣3）2，解得：m=9710，则点C坐标为（9710，0）．综上所述：存在，点C的坐标为：（±410，0）或（5222±，0）或（9710，0）；（3）过点P作y轴的平行线交AB于点H．设直线AB的表达式为y=kx﹣3，把点B坐标代入上式，9=5k﹣3，则k125=，故函数的表达式为：y125=x﹣3，设点P坐标为（m，12 5m2485-m﹣3），则点H坐标为（m，125m﹣3），S△PAB12=•PH•x B52=（125-m2+12m）=－6m2+30m=25756()22m--+，当m=52时，S△PAB取得最大值为：752．答：△PAB的面积最大值为752．【点睛】本题是二次函数综合题．主要考查了二次函数的解析式的求法和与几何图形结合的综合能力的培养．要会利用数形结合的思想把代数和几何图形结合起来，利用点的坐标的意义表示线段的长度，从而求出线段之间的关系．2．如图，在平面直角坐标系中，已知矩形ABCD的三个顶点B（1, 0）、C（3, 0）、D（3,4）．以A为顶点的抛物线y＝ax2＋bx＋c过点C．动点P从点A出发，以每秒12个单位的速度沿线段AD向点D运动，运动时间为t秒．过点P作PE⊥x轴交抛物线于点M，交AC 于点N．（1）直接写出点A的坐标，并求出抛物线的解析式；（2）当t为何值时，△ACM的面积最大？最大值为多少？（3）点Q从点C出发，以每秒1个单位的速度沿线段CD向点D运动，当t为何值时，在线段PE上存在点H，使以C、Q、N、H为顶点的四边形为菱形？【答案】（1）A（1，4）；y＝－x2＋2x＋3；（2）当t＝２时，△AＭC面积的最大值为1；（3）2085或20 13．【解析】（1）由矩形的性质得到点A的坐标，由抛物线的顶点为A，设抛物线的解析式为y＝a（x －1）2＋4，把点C的坐标代入即可求得a的值；（2）由点P的坐标以及抛物线解析式得到点M的坐标，由A、C的坐标得到直线AC的解析式，进而得到点N的坐标，即可用关于t的式子表示MN，然后根据△ACM的面积是△AMN和△CMN的面积和列出用t表示的△ACM的面积，利用二次函数的性质即可得到当t＝２时，△AＭC面积的最大值为1；（3）①当点Ｈ在Ｎ点上方时，由PＮ＝CQ，PN∥CQ，得到四边形PNCQ为平行四边形，所以当PQ＝CQ时，四边形FECQ为菱形，据此得到，解得t值；②当点Ｈ在Ｎ点下方时，NH=CQ=，NQ＝CQ时，四边形NHCQ为菱形，NQ2＝CQ2，得：，解得t值．解：（1）由矩形的性质可得点A（1，4），∵抛物线的顶点为A，设抛物线的解析式为y＝a（x－1）2＋4，代入点C （3, 0），可得a ＝－1． ∴y ＝－（x －1）2＋4＝－x 2＋2x ＋3． （2）∵P （112t +，４）， 将112x t =+代入抛物线的解析式，y ＝－（x －1）2＋4＝2144t -， ∴M （112t +，2144t -）， 设直线AC 的解析式为，将A （１,４），C （３,０）代入，得：，将112x t =+代入得，∴N （112t +，），∴MN ，∴，∴当t ＝２时，△A ＭC 面积的最大值为1． （3）①如图１，当点Ｈ在Ｎ点上方时， ∵Ｎ（112t +，），P （112t +，４）， ∴P Ｎ＝４—（）＝＝CQ ，又∵PN ∥CQ ，∴四边形PNCQ 为平行四边形， ∴当PQ ＝CQ 时，四边形FECQ 为菱形， PQ 2＝PD 2+DQ 2 ＝，∴，整理，得240800t t -+=．解得12085t =-，22085t =+（舍去）；②如图２当点Ｈ在Ｎ点下方时，NH=CQ=，NQ ＝CQ 时，四边形NHCQ 为菱形， NQ 2＝CQ 2，得：．整理，得213728000t t -+=．()()1320400t t --=．所以12013t =，（舍去）．“点睛”此题主要考查二次函数的综合问题，会用顶点式求抛物线，会用两点法求直线解析式，会设点并表示三角形的面积，熟悉矩形和菱形的性质是解题的关键.3．抛物线2y x bx c =-++（b ，c 为常数）与x 轴交于点()1,0x 和()2,0x ，与y 轴交于点A ，点E 为抛物线顶点。

2010年中考数学真题分类汇编(150套)专题十八·二次函数的图象和性质228．2010广东中山如图12所示矩形ABCD的边长AB 6BC 4点F在DC上DF 2．．．．．答案①当时解得②当时此方程无实数根③时解得不合题意舍去综上当或时ΔPQW为直角三角形当0≤x＜或＜x＜4时ΔPQW不为直角三角形3①当0≤x≤4即M从D到A运动时只有当x 4时MN的值最小等于2②当4＜x≤6时当x 5时取得最小值2∴当x 5时线段MN最短MN ．29．2010湖南常德如图已知抛物线与轴交于A －4 和B 10 两点与轴交于C点．求此抛物线的解析式设E是线段AB上的动点作EFAC交BC于F连接CE当△CEF的面积是△BEF 面积的2倍时求E点的坐标若P为抛物线上AC两点间的一个动点过P作轴的平行线交AC于Q当P点运动到什么位置时线段PQ的值最大并求此时P点的坐标．解1由二次函数与轴交于两点可得解得故所求二次函数的解析式为．2∵S△CEF 2 S△BEF ∴∵EFAC ∴∴△BEF～△BAC∴得故E点的坐标为 0 3解法一由抛物线与轴的交点为则点的坐标为0－2．若设直线的解析式为则有解得故直线的解析式为．若设点的坐标为又点是过点所作轴的平行线与直线的交点则点的坐标为．则有＝＝即当时线段取大值此时点的坐标为－2－3解法二延长交轴于点则．要使线段最长则只须△的面积取大值时即可设点坐标为则有＝＝＝＝＝＝－即时△的面积取大值此时线段最长则点坐标为－2－3与y轴交于点AE0b为y轴上一动点过点E的直线与抛物线交于点BC1求点A的坐标2 当b 0时如图2与的面积大小关系如何当时上述关系还成立吗为什么3是否存在这样的b使得是以BC为斜边的直角三角形若存在求出b若不存在说明理由答案1将x 0代入抛物线解析式得点A的坐标为0－42当b＝0时直线为由解得所以BC的坐标分别为－2－222所以利用同底等高说明面积相等亦可当时仍有成立理由如下由解得所以BC的坐标分别为－－bb作轴轴垂足分别为FG则而和是同底的两个三角形所以3存在这样的b因为所以所以即E为BC的中点所以当OE CE时为直角三角形因为所以而所以解得所以当b＝4或－2时ΔOBC为直角三角形31．2010湖南怀化图9是二次函数的图象其顶点坐标为M 1-41求出图象与轴的交点AB的坐标2在二次函数的图象上是否存在点P使若存在求出P点的坐标若不存在请说明理由3将二次函数的图象在轴下方的部分沿轴翻折图象的其余部分保持不变得到一个新的图象请你结合这个新的图象回答当直线与此图象有两个公共点时的取值范围答案解 1 因为M 1-4 是二次函数的顶点坐标所以令解之得∴AB两点的坐标分别为A-10B302 在二次函数的图象上存在点P使设则又∴∵二次函数的最小值为-4∴当时故P点坐标为-25或457分3如图1当直线经过A点时可得8分当直线经过B点时可得由图可知符合题意的的取值范围为解得∴抛物线的解析式是y x2x2．3设PQ的运动时间为t秒则BP tCQ t．以PQC为顶点的三角形为等腰三角形可分三种情况讨论．①若CQ PC如图所示则PC CQ BP t．∴有2t BC ∴t ．②若PQ QC如图所示过点Q作DQ⊥BC交CB于点D则有CD PD．由△ABC∽△QDC可得出PD CD ∴解得t ．③若PQ PC如图所示过点P作PE⊥AC交AC于点E则EC QE PC∴t -t解得t ．4当CQ PC时由3知t ∴点P的坐标是21∴直线OP的解析式是y x因而有x x2x2即x2-2x-4 0解得x 1±∴直线OP与抛物线的交点坐标为1和1-．33．2010湖北省咸宁已知二次函数的图象与轴两交点的坐标分别为00．1证明2若该函数图象的对称轴为直线试求二次函数的最小值．1证明依题意是一元二次方程的两根．根据一元二次方程根与系数的关系得．∴．∴．2解依题意∴．由1得．∴．∴二次函数的最小值为．的图象与x轴交于AB两点 A点在原点的左侧B点的坐标为30与y轴交于C0-3点点P是直线BC下方的抛物线上一动点1求这个二次函数的表达式．2连结POPC并把△POC沿CO翻折得到四边形POPC 那么是否存在点P使四边形POPC为菱形若存在请求出此时点P的坐标若不存在请说明理由．3当点P运动到什么位置时四边形 ABPC的面积最大并求出此时P点的坐标和四边形ABPC的最大面积答案解1将BC两点的坐标代入得解得所以二次函数的表达式为2存在点P使四边形POPC为菱形．设P点坐标为xPP交CO于E若四边形POPC是菱形则有PC＝PO．连结PP 则PE⊥CO于E∴OE EC∴．∴解得不合题意舍去∴P点的坐标为8分3过点P作轴的平行线与BC交于点Q与OB交于点F设Px易得直线BC的解析式为则Q点的坐标为xx－3当时四边形ABPC的面积最大此时P点的坐标为四边形ABPC的面积．35．2010北京在平面直角坐标系xOy中抛物线与x轴的交点分别为原点O 和点A点B2n在这条抛物线上．1求B点的坐标2点P在线段OA上从O点出发向A点运动过P点作x轴的垂线与直线OB交与点E延长PE到点D使得ED PE以PD为斜边在PD右侧做等等腰直角三角形PCD 当P点运动时C点D点也随之运动．①当等腰直角三角形PCD的顶点C落在此抛物线上时求OP的长②若P点从O点出发向A点作匀速运动速度为每秒1个单位同时线段OA 上另一个点Q从A点出发向O点作匀速运动速度为每秒2个单位当Q点到达O 点时停止运动P点也同时停止运动．过Q点做x轴的垂线与直线AB交与点F延长QF到点M使得FM QF以QM为斜边在QM的左侧作等腰直角三角形QMN当Q点运动时M点N点也随之运动．若P点运动到t秒时两个等腰直角三角形分别有一条边恰好落在同一条直线上求此刻t的值．解1∵抛物线经过原点∴m23m2 0解的m1 1m2 2由题意知m≠1∴m 2∴抛物线的解析式为∵点B2n在抛物线n 4∴B点的坐标为242①设直线OB的解析式为y k1x求得直线OB的解析式y 2x∵A点是抛物线与x轴的一个交点可求得A点的坐标为100设P点的坐标为a0则E点的坐标为a2a．根据题意做等腰直角三角形PCD如图1可求得点C的坐标为3a2a有C点在抛物线上得2a －x3a2x3a即a2 a 0解得 a1 a2 0舍去∴OP②依题意作等腰直角三角形QMN设直线AB的解析式y k2xb由点A 10 0 点B24求得直线AB的解析式为y －x5当P点运动到t秒时两个等腰直角三角形分别有一条边恰好落在同一条直线上有以下三种情况第一种情况CD与NQ在同一条直线上如图2所示可证△DPQ为等腰直角三角形．此时QPOPAQ的长可依次表示为t 4t 2t个单位．∴PQ DP 4t∴t4t2t 10∴t第二种情况PC与MN在同一条直线上如图3所示．可证△PQM为等腰直角三角形．此时OPAQ的长依次表示为t2t个单位∴OQ 10 － 2t∵F点在直线AB上∴FQ t∵MQ 2t∴PQ MQ CQ 2t∴t2t2t 10∴t 2第三种情况点PQ重合时PDQM在同一条直线上如图4所示此时OPAQ的长依次表示为t2t个单位．∴t2t 10∴t综上符合题意的值分别为2．红河自治州二次函数的图像如图8所示请将此图像向右平移1个单位再向下平移2个单位1画出经过两次平移后所得到的图像并写出函数的解析式2求经过两次平移后的图像与x轴的交点坐标指出当x满足什么条件时函数值大于0解画图如图所示依题意得∴平移后图像的解析式为2当y 0时 0∴平移后的图像与x轴交与两点坐标分别为0和0由图可知当x 时二次函数的函数值大于02010云南楚雄已知如图抛物线与轴相交于两点A 10 B 30 与轴相较于点C03．1求抛物线的函数关系式2若点D是抛物线上一点请求出的值并求处此时△ABD 的面积．答案解1由题意可知解得所以抛物线的函数关系式为．2把D代人函数解析式中得．所以．顶点为C11且过原点O过抛物线上一点Pxy向直线作垂线垂足为M 连FM如图1求字母abc的值2在直线x＝1上有一点求以PM为底边的等腰三角形PFM的P点的坐标并证明此时△PFM为正三角形3对抛物线上任意一点P是否总存在一点N1t使PM＝PN恒成立若存在请求出t值若不存在请说明理由答案1a＝－1b＝2c＝02过P作直线x 1的垂线可求P的纵坐标为横坐标为此时MP＝MF＝PF＝1故△MPF为正三角形3不存在因为当t＜x＜1时PM与PN不可能相等同理当t＞x＞1时PM与PN 不可能相等39．2010河南在平面直角坐标系中已知抛物线经过A 40 B 0一4 C 20 三点1 求抛物线的解析式2 若点M为第三象限内抛物线上一动点点M的横坐标为m△AMB的面积为S 求S关于m的函数关系式并求出S的最大值3 若点P是抛物线上的动点点Q是直线y －x上的动点判断有几个位置能使以点PQB0为顶点的四边形为平行四边形直接写出相应的点Q的坐标答案1设抛物线的解析式为y ax2bxc a≠0 则有解得∴抛物线的解析式y x2x－42过点M作MD⊥x轴于点D设M点的坐标为mn则AD m4MD －nn m2＋m－4∴S S△AMDS梯形DMBO－S△ABOm4 －n ＋－n＋4 －m －×4×4－2n-2m-8－2 m2＋m－4 -2m-8－m2-4m －4 m 0∴S最大值 43满足题意的Q点的坐标有四个分别是-4 4 4 -4-22－-2－2＋40．2010四川乐山如图 131 抛物线y＝x2bxc与x轴交于AB两点与y轴交于点C 02 连接AC若tan∠OAC＝2．1 求抛物线对应的二次函数的解析式2 在抛物线的对称轴l上是否存在点P使∠APC＝90°若存在求出点P的坐标若不存在请说明理由3 如图 132 所示连接BCM是线段BC上不与BC重合的一个动点过点M 作直线l′‖l交抛物线于点N连接CNBN设点M的横坐标为t．当t为何值时△BCN的面积最大最大面积为多少答案解1∵抛物线y x2＋bx＋c过点C 02 ∴x 2又∵tan∠OAC 2 ∴OA 1即A 10又∵点A在抛物线y x2＋bx＋2上∴0 12＋b×1＋2b －3∴抛物线对应的二次函数的解析式为y x2－3x＋22存在过点C作对称轴l的垂线垂足为D如图所示∴x －∴AE OE-OA -1 ∵∠APC 90°∴tan∠PAE tan∠CPD∴即解得PE 或PE∴点P的坐标为或备注可以用勾股定理或相似解答3如图易得直线BC的解析式为y -x＋2∵点M是直线l′和线段BC的交点∴M点的坐标为t-t2 0＜t＜2∴MN -t2- t2－3t＋2 - t2＋2t∴S△BCM S△MNCS△MNB MNtMN 2-tMN t2-t MN - t2＋2t 0＜t＜2∴S△BCN - t2＋2t - t-1 21∴当t 1时S△BCN的最大值为141．2010江苏徐州如图已知二次函数y的图象与y轴交于点A与轴交于BC两点其对称轴与轴交于点D连接AC．1 点A的坐标为点C的坐标为2 线段AC上是否存在点E使得△EDC为等腰三角形若存在求出所有符合条件的点E的坐标若不存在请说明理由3 点P为轴上方的抛物线上动连接PAPC若所得△PAC的面积为S则S取何值时相应的点P有2个三点1求此抛物线的解析式2以OA的中点M为圆心OM长为半径作⊙M在1中的抛物线上是否存在这样的点P过点P作⊙M的切线l 且l与x轴的夹角为30°若存在请求出此时点P的坐标若不存在请说明理由注意本题中的结果可保留根号答案解1设抛物线的解析式为由题意得解得∴抛物线的解析式为2存在抛物线的顶点坐标是作抛物线和⊙M如图⊙M相切于点C连接MC过C作CD⊥ x 轴于D ∵ MC OM 2 ∠CBM 30° CM⊥BC∴∠BCM 90°∠BMC 60° BM 2CM 4 ∴B -2 0 在Rt△CDM中∠DCM ∠CDM - ∠CMD 30°∴D 1 CD ∴ C 1设线的解析式为点BC在上可得∴切线BC的解析式为∵点P为抛物线与切线的交点由解得∴点P的坐标为∵抛物线的对称轴是直线此抛物线⊙M都与直线成轴对称图形于是作切线 l 关于直线的对称直线 l′如图得到BC关于直线的对称点B1C1l′满足题中要求由对称性得到P1P2关于直线的对称点即为所求的点∴这样的点P共有4个43．2010陕西西安如图在平面直角坐标系中抛物线经过A10B30C01三点 1求该抛物线的表达式2点Q在y轴上点P在抛物线上要使以点QPAB为顶点的四边形是平行四边形求所有满足条件的点P的坐标答案解1设该抛物线的表达式为根据题意得解之得∴所求抛物线的表达式为2①当AB为边时只要PQAB且PQ AB 4即可又知点Q在y轴上∴点P的横坐标为4或-4这时将合条件的点P有两个分别记为P1P2而当x 4时此时②当AB为对角线时只要线段PQ与线段AB互相平分即可又知点Q在y轴上且线段AB中点的横坐标为1∴点P的横坐标为2这时符合条件的点P只有一个记为P3而当x 2时y -1此时P32-1综上满足条件的点44．2010四川内江如图抛物线y＝x2―2mx―3m m＞0 与x轴交于AB两点与y轴交于C点1抛物线AB两点2△BCM与△A的面积比不变求出这个比值3抛物线答案解1y＝x2―2mx―3m＝m x2―2x―3 ＝m x－1 2―4m∴抛物线―4m 2分∵抛物线y＝x2―2mx―3m m＞0 与x轴交于AB两点∴当y＝0时mx2―2mx―3m＝0∵m＞0∴x2―2x―3＝0解得x1＝－1x2＝3∴AB两点2y＝―3C的坐标为0－3∴S△ABC＝××－3＝6＝6mMD⊥x轴于D ∴S△BCM＝S△＋SOCMD－S△＝ OC＋DM ·OD－OB·OC＝×2×4m＋3m＋4－＝∴ S△BCMS△A＝1 8分3抛物线CN＝OD＝1①如果△BCM是Rt△且∠BMC＝90°时CM2＋BM2＝BC2 即1＋m2＋4＋16m2＝9＋9m2解得m＝±∵m＞0∴m＝∴存在抛物线y＝x2－x使得△BCM是Rt△ 10分②①如果△BCM是Rt△且∠BCM＝90°时BC2＋CM2＝BM2即9＋9m2＋1＋m2＝4＋16m2解得m＝±1∵m＞0∴m＝1∴存在抛物线y＝x2－x－3使得△BCM是Rt△③如果△BCM是Rt△且∠CBM＝90°时BC2＋BM2＝CM2即9＋9m2＋4＋16m2＝1＋m2整理得m2＝－此方程无解∴以∠CBM为直角的直角三角形不存在或∵9＋9m2＞1＋m24＋16m2＞1＋m2∴以∠CBM为直角的直角三角形不存在综上的所述存在抛物线y＝x2－x和y＝x2－x－3使得△BCM是Rt△45．2010广东东莞已知二次函数的图象如图所示它与轴的一个交点坐标为－10与轴的交点坐标为03⑴求出bc的值并写出此时二次函数的解析式⑵根据图象写出函数值y为正数时自变量x的取值范围．答案⑴根据题意得解得所以抛物线的解析式为⑵令解得根据图象可得当函数值y为正数时自变量x的取值范围是－1＜＜3．46．2010 福建三明已知抛物线经过点B20和点C08且它的对称轴是直线 1求抛物线与轴的另一交点A坐标2分2求此抛物线的解析式3分3连结ACBC若点E是线段AB上的一个动点与点A点B不重合过点E作EF‖AC交BC于点F连结CE设AE的长为m△CEF的面积为S求S与m之间的函数关系式4在3的基础上试说明S是否存在最大值若存在请求出S的最大值并求出此时点E的坐标判断此时△BCE的形状若不存在请说明理由答案1∵抛物线的对称轴是直线∴由对称性可得A点的坐标为-60 2分2∵点C08在抛物线的图象上将A-60B20代入表达式得解得∴所求解析式为[也可用] 5分3依题意AE m则BE 8-m∵OA 6OC 8∴AC 10∵EFAC ∴≌过点F作FG⊥AB垂足为G则10分4存在理由如下∴当m 4时S有最大值S最大值 8 12分∵m 4∴点E的坐标为-20为等腰三角形14分47．2010湖北襄樊如图7四边形ABCD是平行四边形AB 4OB 2抛物线过ABC 三点与x轴交于另一点D．一动点P以每秒1个单位长度的速度从B点出发沿BA 向点A运动运动到点A停止同时一动点Q从点D出发以每秒3个单位长度的速度沿DC向点C运动与点P同时停止．1求抛物线的解析式2若抛物线的对称轴与AB交于点E与x轴交于点F当点P运动时间t为何值时四边形POQE是等腰梯形3当t为何值时以PBO为顶点的三角形与以点QBO为顶点的三角形相似图7答案解得∴所求抛物线的解析式为．2将抛物线的解析式配方得．∴抛物线的对称轴为x 2．∴D80E22F20．欲使四边形POQE为等腰梯形则有OP QE．即BP FQ．∴t 6－3t即t ．3欲使以PBO为顶点的三角形与以点QBO为顶点的三角形相似∵∠PBO ∠BOQ 90°∴有或即PB OQ或OB2 PB·QO．①若PQ在y轴的同侧．当PB OQ时t 8－3t∴t 2．时．②若PQ在y轴的侧．当PB OQ时∴t 4．时．∵t 0．故舍去∴t ．∴当t 2或t 或t 4或t 秒时以PBO为顶点的三角形与以点QBO为顶点的三角形相似．48．2010 山东东营如图已知二次函数的图象与坐标轴交于点A-1 0和点B0-5．1求该二次函数的解析式2已知该函数图象的对称轴上存在一点P使得△ABP的周长最小．请求出点P的坐标．答案解1根据题意得2分 3分．4分的图象与x轴的另一个交点坐标C5 05分由于P是对称轴上一点连结AB由于要使△ABP的周长最小只要最小6分由于点A与点C关于对称轴对称连结BC交对称轴于点P则 BPPC BC根据两点之间线段最短可得的最小值为BC因而BC与对称轴的交点P就是所求的点8分设直线BC的解析式为根据题意可得解得所以直线BC的解析式为9分因此直线BC与对称轴的交点坐标是方程组的解解得所求的点P的坐标为2-310分49．2010 四川绵阳如图抛物线y ax2 bx 4与x轴的两个交点分别为A －40B20与y轴交于点C顶点为D．E12为线段BC的中点BC的垂直平分线与x 轴y轴分别交于FG．1求抛物线的函数解析式并写出顶点D的坐标2在直线EF上求一点H使△CDH的周长最小并求出最小周长3若点K在x轴上方的抛物线上运动当K运动到什么位置时△EFK的面积最大并求出最大面积．答案1由题意得解得b －1．所以抛物线的解析式为顶点D的坐标为－1．2设抛物线的对称轴与x轴交于点M．因为EF垂直平分BC即C关于直线EG 的对称点为B连结BD交于EF于一点则这一点为所求点H使DH CH最小即最小为DH CH DH HB BD ．而．∴△CDH的周长最小值为CD DR CH ．设直线BD的解析式为y k1x b则解得 b1 3．所以直线BD的解析式为y x 3．由于BC 2CE BC∕2 Rt△CEG∽△COB得 CE CO CG CB所以 CG 25GO 15．G015．同理可求得直线EF的解析式为y x ．联立直线BD与EF的方程解得使△CDH的周长最小的点H．3设KtxF＜t＜xE．过K作x轴的垂线交EF于N．则 KN yK－yN －t ．所以 S△EFK S△KFN S△KNE KNt 3KN1－t 2KN －t2－3t 5 －t 2 ．即当t －时△EFK的面积最大最大面积为此时K－．50．2010 湖北孝感如图已知二次函数图像的顶点坐标为20直线与二次函数的图像交于AB两点其中点A在y轴上1二次函数的解析式为y 3分2证明点不在1中所求的二次函数的图像上3分3若C为线段AB的中点过C点作轴于E点CE与二次函数的图像交于D点①y轴上存在点K使以KADC为顶点的四边形是平行四边形则K点的坐标是 2分②二次函数的图像上是否存在点P使得若存在求出P点坐标若不存在请说明理由4分答案1解3分2证明设点的图像上则有4分整理得∴原方程无解5分的图象上6分说明由从而判断点不在二次函数图像上的同样给分3解①8分②二次函数的图象上存在点P使得如图过点B作轴于F则BFCEAO又C为AB中点9分设由题意有10分解得11分12分说明在求出得到△POE的边OE上的高为16即点P的纵坐标为16然后由可求出P点坐标2010 江苏镇江运算求解已知二次函数的图象C1与x轴有且只有一个公共点1求C1的顶点坐标2将C1向下平移若干个单位后得抛物线C2如果C2与x轴的一个交点为A30求C2的函数关系式并求C2与x轴的另一个交点坐标3若的取值范围答案1 1分轴有且只有一个公共点∴顶点的纵坐标为0∴C1的顶点坐标为10 2分2设C2的函数关系式为把A30代入上式得∴C2的函数关系式为 3分∵抛物线的对称轴为轴的一个交点为A30由对称性可知它与x轴的另一个交点坐标为10 4分3当的增大而增大当 5分52． 2010江苏苏州本题满分9分如图以A为顶点的抛物线与y轴交于点B．已知AB两点的坐标分别为 30 04 ．1 求抛物线的解析式2 设M mn 是抛物线上的一点 mn为正整数且它位于对称轴的右侧．若以MBOA为顶点的四边形四条边的长度是四个连续的正整数求点M的坐标3 在 2 的条件下试问对于抛物线对称轴上的任意一点PPA2PB2PM2＞28是否总成立请说明理由．答案53．2010广东广州2112分已知抛物线y＝－x22x＋2．1该抛物线的对称轴是顶点坐标选取适当的数据填入下表并在图7的直角坐标系内描点画出该抛物线的图象x y 若该抛物线上两点Ax1y1Bx2y2的横坐标满足x1＞x2＞1试比较y1与y2的大小答案解x＝113x －1 0 1 2 3 y －1 2 3 2 －1因为在对称轴x＝1右侧y随x的增大而减小又x1＞x2＞1所以y1＜y2ＣCD 平行于轴交抛物线于点D写出D点的坐标并求ADBC的交点E的坐标3 若抛物线的顶点为ＰＰCＰD可设抛物线的解析式为则解得∴抛物线的解析式为4分⑵的坐标为 5分直线的解析式为直线的解析式为由求得交点的坐标为 8分⑶连结交于的坐标为又∵∴且∴四边形是菱形12分55．2010江苏南京7分已知点A11在二次函数图像上1用含的代数式表示2如果该二次函数的图像与轴只有一个交点求这个二次函数的图像的顶点坐标答案56．2010江苏盐城本题满分12分已知函数y ax2x1的图象与x轴只有一个公共点．1求这个函数关系式2如图所示设二次函数y ax2x1图象的顶点为B与y轴的交点为AP为图象上的一点若以线段PB为直径的圆与直线AB相切于点B求P点的坐标3在 2 中若圆与x轴另一交点关于直线PB的对称点为M试探索点M是否在抛物线y ax2x1上若在抛物线上求出M点的坐标若不在请说明理由．答案解1当a 0时y x1图象与x轴只有一个公共点 1分当a≠0时△ 1- 4a 0a 此时图象与x轴只有一个公共点．∴函数的解析式为y x1 或y x2x13分2设P为二次函数图象上的一点过点P作PC⊥x轴于点C．∵是二次函数由1知该函数关系式为y x2x1则顶点为B-20图象与y轴的交点坐标为A014分∵以PB为直径的圆与直线AB相切于点B ∴PB⊥AB 则∠PBC ∠BAO ∴Rt△PCB∽Rt△BOA∴故PC 2BC5分设P点的坐标为 xy ∵∠ABO是锐角∠PBA是直角∴∠PBO是钝角∴x -2 ∴BC -2-xPC -4-2x即y -4-2x P点的坐标为 x-4-2x∵点P在二次函数y x2x1的图象上∴-4-2x x2x16分解之得x1 -2x2 -10∵x -2 ∴x -10∴P点的坐标为 -1016 7分3点M不在抛物线上8分由2知C为圆与x 轴的另一交点连接CMCM与直线PB的交点为Q过点M作x 轴的垂线垂足为D取CD的中点E连接QE则CM⊥PB且CQ MQ∴QE‖MDQE MDQE⊥CE∵CM⊥PBQE⊥CE PC⊥x 轴∴∠QCE ∠EQB ∠CPB∴tan∠QCE tan∠EQB tan∠CPBCE 2QE 2×2BE 4BE又CB 8故BE QE∴Q点的坐标为 -可求得M点的坐标为 11分∵≠∴C点关于直线PB的对称点M不在抛物线上12分其它解法仿此得分57．2010辽宁市如图平面直角坐标系中有一直角梯形OMNH点H的坐标为－80点N的坐标为－6－4．1画出直角梯形OMNH绕点O旋转180°的图形OABC并写出顶点ABC的坐标点M的对应点为A 点N的对应点为B 点H的对应点为C2求出过ABC三点的抛物线的表达式3截取CE OF AG m且EFG分别在线段COOAAB上求四边形BEFG的面积S与m 之间的函数关系式并写出自变量m的取值范围面积S是否存在最小值若存在请求出这个最小值若不存在请说明理由4在3的情况下四边形BEFG是否存在邻边相等的情况若存在请直接写出此时m的值并指出相等的邻边若不存在说明理由．1 利用中心对称性质画出梯形OABC． 1分∵ABC三点与MNH分别关于点O中心对称∴A04B64C80 3分写错一个点的坐标扣1分2设过ABC三点的抛物线关系式为∵抛物线过点A04∴．则抛物线关系式为． 4分将B64 C80两点坐标代入关系式得解得所求抛物线关系式为．7分3∵OA 4OC 8∴AF 4－mOE 8－m． 8分∴OAABOCAFAGOE·OFCE·OA0＜＜4 10分∵．∴当时S的取最小值．又∵0＜m＜4∴不存在m值使S的取得最小值． 2分4当时GB GF当时BE BG．14分的抛物线交轴于点交轴于两点点在点的左侧已知点坐标为1求此抛物线的解析式2过点作线段的垂线交抛物线于点如果以点为圆心的圆与直线相切请判断抛物线的对称轴与⊙有怎样的位置关系并给出证明3已知点是抛物线上的一个动点且位于两点之间问当点运动到什么位置时的面积最大并求出此时点的坐标和的最大面积答案1解设抛物线为∵抛物线经过点03∴∴∴抛物线为 2 答与⊙相交证明当时∴为20为60∴设⊙与相切于点连接则∵∴又∵∴∴∽∴∴∴6分∵抛物线的对称轴为∴点到的距离为2∴抛物线的对称轴与⊙相交3 解过点作平行于轴的直线交于点求的解析式为设点的坐标为则点的坐标为∴∵∴当时的面积最大为此时点的坐标为359．2010甘肃兰州本题满分11分如图1已知矩形ABCD的顶点A与点O重合ADAB分别在x轴y轴上且AD 2AB 3抛物线经过坐标原点O和x轴上另一点E401当x取何值时该抛物线的最大值是多少2将矩形ABCD以每秒1个单位长度的速度从图1所示的位置沿x轴的正方向匀速平行移动同时一动点P也以相同的速度从点A出发向B匀速移动设它们运动的时间为t秒0≤t≤3直线AB与该抛物线的交点为N如图2所示①当时判断点P是否在直线ME上并说明理由②以PNCD为顶点的多边形面积是否可能为5若有可能求出此时N点的坐标若无可能请说明理由．图1 图2答案经过坐标原点O00和点E40故可得c 0b 4所以抛物线的解析式为1分由得当x 2时该抛物线的最大值是4 2分2①点P不在直线ME上已知M点的坐标为 24 E点的坐标为 40设直线ME的关系式为y kxb于是得解得所以直线ME的关系式为y -2x8 3分由已知条件易得当时OA AP 4分∵ P点的坐标不满足直线ME的关系式y -2x8 [来源ZxxkCom] ∴当时点P不在直线ME上 5分②以PNCD为顶点的多边形面积可能为5∵点A在x轴的非负半轴上且N在抛物线上∴ OA AP t∴点PN的坐标分别为 tt t-t 24t 6分∴ AN -t 24t 0≤t≤3∴ AN-AP -t 24 t - t -t 23 t t 3-t ≥0 ∴ PN -t 23 t7分ⅰ当PN 0即t 0或t 3时以点PNCD为顶点的多边形是三角形此三角形的高为AD∴ S DC·AD ×3×2 3ⅱ当PN≠0时以点PNCD为顶点的多边形是四边形∵ PN‖CDAD⊥CD∴ S CDPN ·AD [3 -t 23 t ]×2 -t 23 t38分当-t 23 t3 5时解得t 129分而12都在0≤t≤3范围内故以PNCD为顶点的多边形面积为5综上所述当t 12时以点PNCD为顶点的多边形面积为5当t 1时此时N点的坐标1310分当t 2时此时N点的坐标2411分说明ⅱ中的关系式当t 0和t 3时也适合故在阅卷时没有ⅰ只有ⅱ也可以不扣分60．2010山东青岛已知把Rt△ABC和Rt△DEF按如图1摆放点C与点E重合点BCEF在同一条直线上．∠ACB∠EDF 90°∠DF 45°AC 8 cmBC6 cmEF9 cm．△DEF从图1的位置出发以1 cms的速度沿CB△ABC匀速移在△DEF移的同时点P从△ABC的顶点B出发以2 cms的速度沿BA向点A动△DEF的顶点D移动到AC边上时△DEF停止移．DE与AC相交于点Q连接PQ设动时间为ts0＜t＜45．1当t为何值时点A在线段PQ的垂直平分线上2连接PE设四边形APE的面积为ycm2求y与之间的函数关系式是否存在某一时刻t使面积y最小若存在求出y的最小值若不存在说明理由．3是否存在某一时刻t使PQF三点在同一条直线上若存在求出此时t的值若不存在说明理由．答案解1∵点A在线段PQ的垂直平分线上∴AP AQ∵∠DEF 45°∠ACB 90°∠∠ACB＋∠EQC 180°∴∠EQC 45°∴∠DEF ∠EQC∴CE CQ由题意知CE tBP 2 t。

2010年中考数 学 试 卷*考试时间120分钟 试卷满分150分一、选择题（本大题共7小题，每小题4分，共28分）每题所给的四个选项中只有一项是符合题目要求的，请将所选项的代号字母填在答卷的相应位置处． 1） A． BC．-D2．反比例函数23m y x--=的图象位于（ ）A ．第一、三象限B ．第二、四象限C ．第二、三象限D ．第一、二象限3．从2、3、4、5这四个数中，任取两个数()p q p q ≠和，构成函数2y px y x q =-=+和，并使这两个函数图象的交点在直线2x =的右侧，则这样的有序数对()p q ，共有（ ） A ．12对 B ．6对 C ．5对 D ．3对4．把多项式2288x x -+分解因式，结果正确的是（ ） A ．()224x -B ．()224x -C ．()222x -D ．()222x +5．某等腰三角形的两条边长分别为3cm 和6cm ，则它的周长为（ ） A ．9cm B ．12cm C ．15cm D ．12cm 或15cm6．一次函数y kx b =+（k b ，是常数，0k ≠）的图象如图所示，则不等式0kx b +>的解集是A ．2x >-；B ．0x >；C ．2x <-；D ．0x <7．若0a >且2x a =，3y a =，则x ya -的值为（ ）A ．1-B ．1C ．23D ．32二、填空题（本大题共6小题，每小题4分，共24分）把答案直接填在答卷的相应位置处．xb +8．将点(12)，向左平移1个单位，再向下平移2个单位后得到对应点的坐标是 ．9．幼儿园把新购进的一批玩具分给小朋友．若每人3件，那么还剩余59件；若每人5件，那么最后一个小朋友分到玩具，但不足4件，这批玩具共有 件．10．李师傅随机抽查了本单位今年四月份里6天的日用水量（单位：吨）结果如下：7，8，8，7，6，6，根据这些数据，估计四月份本单位用水总量为 吨．11．我们知道利用相似三角形可以计算不能直接测量的物体的高度，阳阳的身高是1.6m ，他在阳光下的影长是 1.2m ，在同一时刻测得某棵树的影长为 3.6m ，则这棵树的高度约为 m ． 12．如图所示的半圆中，AD 是直径，且3AD =，2AC =，则sin B 的值是 ．13．某个圆锥的侧面展开图形是一个半径为6cm ，圆心角为︒120的扇形，则这个圆锥的底面半径为______________cm ．三、解答题（本大题Ⅰ—Ⅴ题，共10小题，共98分）解答时应在答卷的相应位置处写出文字说明、证明过程或演算过程． Ⅰ．（本题满分12分，第14题6分，第15题6分）14．计算：230116(2)(πtan60)3-⎛⎫--÷-+-- ⎪⎝⎭．15．先化简，再求值：221111121x x x x x +-÷+--+，其中1x =． Ⅱ．（本题满分28分，第16题7分，第17题10分，第18题11分）C BD A16．如图，线段AB 与⊙O 相切于点C ，连结OA ，OB ，OB 交⊙O 于点D ，已知6OA OB ==，AB =（1）求⊙O 的半径； （2）求图中阴影部分的面积．17．响应“家电下乡”的惠农政策，某商场决定从厂家购进甲、乙、丙三种不同型号的电冰箱80台，其中甲种电冰箱的台数是乙种电冰箱台数的2倍，购买三种电冰箱的总金额不超．．过．132 000元．已知甲、乙、丙三种电冰箱的出厂价格分别为：1 200元/台、1 600元/台、2 000元/台．(1)至少购进乙种电冰箱多少台？(2)若要求甲种电冰箱的台数不超过丙种电冰箱的台数，则有哪些购买方案？18．甲、乙两名运动员进行长跑训练，两人距终点的路程y （米）与跑步时间x （分）之间C OABD的函数图象如图所示，根据图象所提供的信息解答问题：(1) 他们在进行 米的长跑训练，在0＜x ＜15的时段内，速度较快的人是 ；(2) 求甲距终点的路程y （米）和跑步时间 x （分）之间的函数关系式； (3) 当x =15时，两人相距多少米？在15＜x ＜20的时段内，求两人速度之差．Ⅲ．（本题满分36分，第19题12分，第20题12分，第21题12分）19．把一副扑克牌中的3张黑桃牌（它们的正面牌面数字分别是3、4、5）洗匀后正面朝下放在桌面上．（1）如果从中随机抽取一张牌，那么牌面数字是4的概率是多少？（2）小王和小李玩摸牌游戏，游戏规则如下：先由小王随机抽出一张牌，记下牌面数字后放回，洗匀后正面朝下，再由小李随机抽出一张牌，记下牌面数字．当2张牌面数字相同时，小王赢；当2张牌面数字不相同时，小李赢．现请你利用树状图或列表法分析游戏规则对双方是否公平？并说明理由．20．如图，河流两岸a b ，互相平行，C D ，是河岸a 上间隔50m 的两个电线杆．某人在河分)岸b 上的A 处测得30DAB ∠= ，然后沿河岸走了100m 到达B 处，测得60CBF ∠=，求河流的宽度CF 的值（结果精确到个位）．21．三个生产日光灯管的厂家在广告中宣称，他们生产的日光灯管在正常情况下，灯管的使用寿命为12个月．工商部门为了检查他们宣传的真实性，从三个厂家各抽取11只日光灯管进行检测，灯管的使用寿命（单位：月）如下：试问：（1）这三个厂家的广告，分别利用了统计中的哪一个特征数（平均数、中位数、众数）进行宣传？（2）如果三种产品的售价一样，作为顾客的你选购哪个厂家的产品？请说明理由．Ⅳ（本题满分8分）BED CFab A22．如图， 已知等边三角形ABC 中，点D ，E ，F 分别为边AB ，AC ，BC 的中点，M 为直线BC 上一动点，△DMN 为等边三角形（点M 的位置改变时， △DMN 也随之整体移动） ． （1）如图①，当点M 在点B 左侧时，请你判断EN 与MF 有怎样的数量关系？点F 是否在直线NE 上？都请直接．．．．写出结论，不必证明或说明理由； （2）如图②，当点M 在BC 上时，其它条件不变，（1）的结论中EN 与MF 的数量关系是否仍然成立?若成立，请利用图②证明；若不成立，请说明理由；（3）若点M 在点C 右侧时，请你在图③中画出相应的图形，并判断（1）的结论中EN 与MF 的数量关系是否仍然成立?若成立?请直接写出结论，不必证明或说明理由．Ⅴ（本题满分14分）图① 图② 图③A·BCD EF··N MFEDCB ANMF EDCBA·23．如图，在平面直角坐标系中，以点(11)C ，为圆心，2为半径作圆，交x 轴于A B ，两点，开口向下的抛物线经过点A B ，，且其顶点P 在C 上．（1）求ACB 的大小；（2）写出A B ，两点的坐标； （3）试确定此抛物线的解析式；（4）在该抛物线上是否存在一点D ，使线段OP 与CD 互相平分？若存在，求出点D 的坐标；若不存在，请说明理由．2010年中考数学试题参考答案及评分标准二、填空题（本大题共6小题，每小题4分，共24分） 8．(00)，；9．152；10．210；11．4.8；12．23；13．4 三、解答题（本大题Ⅰ—Ⅴ题，共10小题，共98分） Ⅰ．（本题满分12分，第14题6分，第15题6分） 14．解：原式＝9－16÷（－8）＋1－23×23……………………2分 ＝9＋2＋1－3.……………………………………4分 ＝9 ………………………………6分15．解：原式211(1)1(1)(1)1x x x x x -=-++-+······································································ 2分 2211(1)(1)1(1)(1)x x x x x x -+--=-=+++ ······························································· 4分 22(1)x =+ ········································································································ 5分当1x =时，原式23== ··································································· 6分 Ⅱ．（本题满分28分，第16题7分，第17题10分，第18题11分）16．（1）连结OC ，则 OC AB ⊥． …………………………………………………1分∵OA OB =，∴1122AC BC AB ===⨯ ………………………………………2分在Rt AOC △中，3OC ===．∴ ⊙O 的半径为3． …………………………………………………………3分 （2）∵ OC =12OB , ∴ ∠B =30o , ∠COD =60o ． ……………………………………5分 ∴扇形OCD 的面积为OCD S 扇形=260π3360⨯⨯=32π． …………………………………5分阴影部分的面积为：Rt Δ=OBC OCD S S S -阴影扇形=12OC CB ⋅－3π2－3π2．…………………………7分 17．解：（1）设购买乙种电冰箱x 台，则购买甲种电冰箱2x 台，丙种电冰箱(803)x -台，根据题意，列不等式： ································································ 1分120021600(803)2000132000x x x ⨯++-⨯≤． ···························································· 3分解这个不等式，得14x ≥． ·································································································· 4分 ∴至少购进乙种电冰箱14台． ····························································································· 5分 （2）根据题意，得2803x x -≤． ····················································································· 6分 解这个不等式，得16x ≤． ·································································································· 7分 由（1）知14x ≥． 1416x ∴≤≤． 又x 为正整数， 141516x ∴=，，． ···················································································································· 8分 所以，有三种购买方案：方案一：甲种电冰箱为28台，乙种电冰箱为14台，丙种电冰箱为38台； 方案二：甲种电冰箱为30台，乙种电冰箱为15台，丙种电冰箱为35台； 方案三：甲种电冰箱为32台，乙种电冰箱为16台，丙种电冰箱为32台． ··················· 10分 18．解：（1）5000…………………………………2分甲 ………………………………4分（2）设所求直线的解析式为：y =kx +b (0≤x ≤20)， ………5分由图象可知：b =5000，当x =20时，y =0， ∴0=20k +5000，解得k = -250. …7分即y = -250x +5000 (0≤x ≤20) ……………7分（3）当x =15时，y = -250x +5000= -250×15+5000=5000-3750=1250. ………8分 两人相距：(5000 -1250)-(5000-2000)=750（米）………………9分 两人速度之差:750÷(20-15)=150（米/分）……………11分Ⅲ．（本题满分36分，第19题12分，第20题12分，第21题12分） 19解：（1）P （抽到牌面数字是4）13=； ········································································ 2分（2）游戏规则对双方不公平． ················································································· 5分 理由如下：由上述树状图或表格知：所有可能出现的结果共有9种． P （抽到牌面数字相同）=3193=， P （抽到牌面数字不相同）=6293=．∵1233<，∴此游戏不公平，小李赢的可能性大． ············································ 12分 （说明：答题时只需用树状图或列表法进行分析即可）20．解：过点C 作CE AD ∥，交AB 于E CD AE ∥，CE AD ∥ ····································································································· 2分∴四边形AECD 是平行四边形 ······························································································ 4分 50AE CD ∴==m ，50EB AB AE =-=m ，30CEB DAB ∠=∠= ···························· 6分又60CBF ∠=，故30ECB ∠=，50CB EB ∴==m ···················································· 8分∴在Rt CFB △中，sin 50sin 6043CF CB CBF =∠=≈m ········································ 11分 答：河流的宽度CF 的值为43m ． ······················································································ 12分21．答：（1）甲厂的广告利用了统计中的平均数． ····························································· 2分乙厂的广告利用了统计中的众数． ············································································ 4分 丙厂的广告利用了统计中的中位数． ············································································ 7分分…………………………8分11F B C （2） 选用甲厂的产品． 因为它的平均数较真实地反映灯管的使用寿命 ······················· 10分 或选用丙厂的产品．因为丙厂有一半以上的灯管使用寿命超过12个月 ··························· 10分Ⅳ．（本题满分8分）22．（1）判断：EN 与MF 相等 （或EN=MF ），点F 在直线NE 上， ········ 2分（2）成立． ······························ 3分 证明：法一：连结DE ，DF ．∵△ABC 是等边三角形， ∴AB =AC =BC ．又∵D ，E ，F 是三边的中点，∴DE ，DF ，EF 为三角形的中位线．∴DE =DF =EF ，∠FDE =60°．又∠MDF +∠FDN =60°， ∠NDE +∠FDN =60°，∴∠MDF =∠NDE ．在△DMF 和△DNE 中，DF =DE ，DM =DN ， ∠MDF =∠NDE ，∴△DMF ≌△DNE ． 8∴MF =NE ． ·························· 6分法二：延长EN ，则EN 过点F ．∵△ABC 是等边三角形， ∴AB =AC =BC ．又∵D ，E ，F 是三边的中点， ∴EF =DF =BF ．∵∠BDM +∠MDF =60°， ∠FDN +∠MDF =60°，∴∠BDM =∠FDN ．又∵DM =DN ， ∠ABM =∠DFN =60°，∴△DBM ≌△DFN ．∴BM =FN ．∵BF =EF ， ∴MF =EN ． ·························· 6分（3）画出图形（连出线段NE ）， 6MF 与EN 相等的结论仍然成立（或MF =NE 成立）． ·············· 8分Ⅴ．（本题满分14分）23．解：（1）作CHN C A B F M D E NC A B F MD E12 1CH = ，半径2CB = ·························································· 1分60BCH ∠= ，120ACB ∴∠= ········································· 3分（2）1CH = ，半径2CB =HB ∴=(1A ，················································ 5分(1B ··············································································· 6分 （3）由圆与抛物线的对称性可知抛物线的顶点P 的坐标为(13)， ······································· 7分 设抛物线解析式2(1)3y a x =-+ ·························································································· 8分把点(1B 代入上式，解得1a =- ·············································································· 9分 222y x x ∴=-++ ·············································································································· 10分 （4）假设存在点D 使线段OP 与CD 互相平分，则四边形OCPD 是平行四边形 ·········· 11分 PC OD ∴∥且PC OD =．PC y ∥轴，∴点D 在y 轴上． ····················································································· 12分又2PC = ，2OD ∴=，即(02)D ，． 又(02)D ，满足222y x x =-++， ∴点D 在抛物线上 ··············································································································· 13分 所以存在(02)D ，使线段OP 与CD 互相平分． ·································································· 14分。

一、二次函数 真题与模拟题分类汇编（难题易错题）1．如图，在平面直角坐标系xOy 中，A 、B 为x 轴上两点，C 、D 为y 轴上的两点，经 过点A 、C 、B 的抛物线的一部分C 1与经过点A 、D 、B 的抛物线的一部分C 2组合成一条封闭曲线，我们把这条封闭曲线称为“蛋线”．已知点C 的坐标为（0，），点M 是抛物线C 2：2y mx 2mx 3m =--（m ＜0）的顶点．（1）求A 、B 两点的坐标；（2）“蛋线”在第四象限上是否存在一点P ，使得△PBC 的面积最大？若存在，求出△PBC 面积的最大值；若不存在，请说明理由；（3）当△BDM 为直角三角形时，求m 的值．【答案】（1）A （，0）、B （3，0）．（2）存在．S △PBC 最大值为2716 （3）2m 2=-或1m =-时，△BDM 为直角三角形． 【解析】【分析】 （1）在2y mx 2mx 3m =--中令y=0，即可得到A 、B 两点的坐标．（2）先用待定系数法得到抛物线C 1的解析式，由S △PBC = S △POC + S △BOP –S △BOC 得到△PBC 面积的表达式，根据二次函数最值原理求出最大值．（3）先表示出DM 2，BD 2，MB 2，再分两种情况：①∠BMD=90°时；②∠BDM=90°时，讨论即可求得m 的值．【详解】解：（1）令y=0，则2mx 2mx 3m 0--=，∵m ＜0，∴2x 2x 30--=，解得：1x 1=-，2x 3=．∴A （，0）、B （3，0）．（2）存在．理由如下：∵设抛物线C 1的表达式为()()y a x 1x 3=+-（a 0≠），把C （0，32-）代入可得，12a =． ∴Ｃ1的表达式为：()()1y x 1x 32=+-，即213y x x 22=--． 设P （p ，213p p 22--）， ∴ S △PBC = S △POC + S △BOP –S △BOC =23327p 4216--+（）． ∵3a 4=-<0，∴当3p 2=时,S △PBC 最大值为2716． （3）由C 2可知： B （3，0），D （0，3m -），M （1，4m -），∴BD 2=29m 9+，BM 2=216m 4+，DM 2=2m 1+．∵∠MBD<90°, ∴讨论∠BMD=90°和∠BDM=90°两种情况：当∠BMD=90°时，BM 2+ DM 2= BD 2，即216m 4+＋2m 1+=29m 9+，解得：12m 2=-,22m 2=(舍去)． 当∠BDM=90°时，BD 2+ DM 2= BM 2，即29m 9+＋2m 1+=216m 4+，解得：1m 1=-，2m 1=(舍去) ．综上所述，2m =-或1m =-时，△BDM 为直角三角形．2．如图，在平面直角坐标系中，抛物线y=ax 2+bx ﹣3（a≠0）与x 轴交于点A （﹣2，0）、B （4，0）两点，与y 轴交于点C ．（1）求抛物线的解析式；（2）点P 从A 点出发，在线段AB 上以每秒3个单位长度的速度向B 点运动，同时点Q 从B 点出发，在线段BC 上以每秒1个单位长度的速度向C 点运动，其中一个点到达终点时，另一个点也停止运动，当△PBQ 存在时，求运动多少秒使△PBQ 的面积最大，最大面积是多少？（3）当△PBQ 的面积最大时，在BC 下方的抛物线上存在点K ，使S △CBK ：S △PBQ =5：2，求K 点坐标．【答案】（1）y=38x 2﹣34x ﹣3（2）运动1秒使△PBQ 的面积最大，最大面积是910 （3）K 1（1，﹣278），K 2（3，﹣158） 【解析】【详解】 试题分析：（1）把点A 、B 的坐标分别代入抛物线解析式，列出关于系数a 、b 的解析式，通过解方程组求得它们的值；（2）设运动时间为t 秒．利用三角形的面积公式列出S △PBQ 与t 的函数关系式S △PBQ =﹣910（t ﹣1）2+910．利用二次函数的图象性质进行解答； （3）利用待定系数法求得直线BC 的解析式为y=34x ﹣3．由二次函数图象上点的坐标特征可设点K 的坐标为（m ，38m 2﹣34m ﹣3）． 如图2，过点K 作KE ∥y 轴，交BC 于点E ．结合已知条件和（2）中的结果求得S △CBK =94．则根据图形得到：S △CBK =S △CEK +S △BEK =12EK•m+12•EK•（4﹣m ），把相关线段的长度代入推知：﹣34m 2+3m=94．易求得K 1（1，﹣278），K 2（3，﹣158）． 解：（1）把点A （﹣2，0）、B （4，0）分别代入y=ax 2+bx ﹣3（a≠0），得 423016430a b a b --=⎧⎨+-=⎩， 解得3834a b ⎧=⎪⎪⎨⎪=-⎪⎩， 所以该抛物线的解析式为：y=38x 2﹣34x ﹣3； （2）设运动时间为t 秒，则AP=3t ，BQ=t ．∴PB=6﹣3t ．由题意得，点C 的坐标为（0，﹣3）． 在Rt △BOC 中，．如图1，过点Q 作QH ⊥AB 于点H ．∴QH ∥CO ，∴△BHQ ∽△BOC ， ∴HB OC BG BC=，即Hb 35t =， ∴HQ=35t ． ∴S △PBQ =12PB•HQ=12（6﹣3t ）•35t=﹣910t 2+95t=﹣910（t ﹣1）2+910． 当△PBQ 存在时，0＜t ＜2∴当t=1时， S △PBQ 最大=910． 答：运动1秒使△PBQ 的面积最大，最大面积是910； （3）设直线BC 的解析式为y=kx+c （k≠0）．把B （4，0），C （0，﹣3）代入，得403k c c +=⎧⎨=-⎩， 解得3k 4c 3⎧=⎪⎨⎪=-⎩，∴直线BC 的解析式为y=34x ﹣3． ∵点K 在抛物线上． ∴设点K 的坐标为（m ，38m 2﹣34m ﹣3）． 如图2，过点K 作KE ∥y 轴，交BC 于点E ．则点E 的坐标为（m ，34m ﹣3）．∴EK=34m﹣3﹣（38m2﹣34m﹣3）=﹣38m2+32m．当△PBQ的面积最大时，∵S△CBK：S△PBQ=5：2，S△PBQ=9 10．∴S△CBK=94．S△CBK=S△CEK+S△BEK=12EK•m+12•EK•（4﹣m）=12×4•EK=2（﹣38m2+32m）=﹣34m2+3m．即：﹣34m2+3m=94．解得 m1=1，m2=3．∴K1（1，﹣278），K2（3，﹣158）．点评：本题是二次函数的综合题型，其中涉及到的知识点有待定系数法求二次函数解析式和三角形的面积求法．在求有关动点问题时要注意该点的运动范围，即自变量的取值范围．3．已知，m，n是一元二次方程x2+4x+3=0的两个实数根，且|m|＜|n|，抛物线y=x2+bx+c 的图象经过点A（m，0），B（0，n），如图所示．（1）求这个抛物线的解析式；（2）设（1）中的抛物线与x轴的另一个交点为抛物线的顶点为D，求出点C，D的坐标，并判断△BCD的形状；（3）点P是直线BC上的一个动点（点P不与点B和点C重合），过点P作x轴的垂线，交抛物线于点M，点Q在直线BC上，距离点P2个单位长度，设点P的横坐标为t，△PMQ的面积为S，求出S与t之间的函数关系式．【答案】（1）223y x x =--；（2）C （3，0），D （1，﹣4），△BCD 是直角三角形；（3）2213(03)2213(03)22t t t S t t t t ⎧-+⎪⎪=⎨⎪-⎪⎩＜＜＜或＞ 【解析】试题分析：（1）先解一元二次方程，然后用待定系数法求出抛物线解析式；（2）先解方程求出抛物线与x 轴的交点，再判断出△BOC 和△BED 都是等腰直角三角形，从而得到结论；（3）先求出QF=1，再分两种情况，当点P 在点M 上方和下方，分别计算即可． 试题解析：解（1）∵2+430x x +=，∴11x =-，23x =-，∵m ，n 是一元二次方程2+430x x +=的两个实数根，且|m|＜|n|，∴m=﹣1，n=﹣3，∵抛物线223y x x =--的图象经过点A （m ，0），B （0，n ），∴10{3b c c -+==-，∴2{3b c =-=-，∴抛物线解析式为223y x x =--；（2）令y=0，则2230x x --=，∴11x =-，23x =，∴C （3，0），∵223y x x =--=2(1)4x --，∴顶点坐标D （1，﹣4），过点D 作DE ⊥y 轴，∵OB=OC=3，∴BE=DE=1，∴△BOC 和△BED 都是等腰直角三角形，∴∠OBC=∠DBE=45°，∴∠CBD=90°，∴△BCD 是直角三角形；（3）如图，∵B （0，﹣3），C （3，0），∴直线BC 解析式为y=x ﹣3，∵点P 的横坐标为t ，PM ⊥x 轴，∴点M 的横坐标为t ，∵点P 在直线BC 上，点M 在抛物线上，∴P （t ，t ﹣3），M （t ，223t t --），过点Q 作QF ⊥PM ，∴△PQF 是等腰直角三角形，∵2，∴QF=1．①当点P 在点M 上方时，即0＜t ＜3时，PM=t ﹣3﹣（223t t --）=23t t -+，∴S=12PM×QF=21(3)2t t -+=21322t t -+，②如图3，当点P 在点M 下方时，即t ＜0或t ＞3时，PM=223t t --﹣（t ﹣3）=23t t -，∴S=12PM×QF=12（23t t -）=21322t t -．综上所述，S=2213 (03)22{13 (03)22t t t t t t t 或-+<<-．考点：二次函数综合题；分类讨论．4．如图所示，已知平面直角坐标系xOy ，抛物线过点A(4,0)、B(1,3)(1)求该抛物线的表达式，并写出该抛物线的对称轴和顶点坐标；(2)记该抛物线的对称轴为直线l ，设抛物线上的点P(m,n)在第四象限，点P 关于直线l 的对称点为E ，点E 关于y 轴的对称点为F ，若四边形OAPF 的面积为20，求m 、n 的值.【答案】(1)y=-224(2)4y x x x =-+=--+，对称轴为：x=2，顶点坐标为：（2，4）(2)m 、n 的值分别为 5，-5【解析】（1） 将点A(4,0)、B(1,3) 的坐标分别代入y ＝－x 2＋bx ＋c ，得：4b+c-16=0，b+c-1="3" ，解得：b="4" ， c=0．所以抛物线的表达式为：24y x x =-+．y=-224(2)4y x x x =-+=--+，所以 抛物线的对称轴为：x=2，顶点坐标为：（2，4）．（2） 由题可知，E 、F 点坐标分别为（4-m ，n ），（m-4，n ）．三角形POF 的面积为：1/2×4×|n|= 2|n|，三角形AOP 的面积为：1/2×4×|n|= 2|n|，四边形OAPF 的面积= 三角形POF 的面积+三角形AOP 的面积=20，所以 4|n|=20， n=-5．（因为点P(m,n)在第四象限，所以n<0）又n=-2m +4m ，所以2m -4m-5=0，m=5．（因为点P(m,n)在第四象限，所以m>0)故所求m 、n 的值分别为 5，-5．5．如图，已知点A （0，2），B （2，2），C （-1，-2），抛物线F ：y=x 2-2mx+m 2-2与直线x=-2交于点P ．（1）当抛物线F 经过点C 时，求它的解析式；（2）设点P 的纵坐标为y P ，求y P 的最小值，此时抛物线F 上有两点（x 1，y 1），（x 2，y 2），且x 1＜x 2≤-2，比较y 1与y 2的大小.【答案】(1) 221y x x =+-；(2)12y y >.【解析】【分析】 （1）根据抛物线F ：y=x 2-2mx+m 2-2过点C （-1，-2），可以求得抛物线F 的表达式； （2）根据题意，可以求得y P 的最小值和此时抛物线的表达式，从而可以比较y 1与y 2的大小.【详解】(1) ∵抛物线F 经过点C （－1，－2），∴22122m m -=++-.∴m 1=m 2=-1.∴抛物线F 的解析式是221y x x =+-.(2)当x=-2时，2442P y m m =++-=()222m +-. ∴当m=-2时，P y 的最小值为－2.此时抛物线F 的表达式是()222y x =+-.∴当2x ≤-时，y 随x 的增大而减小.∵12x x <≤－2，∴1y >2y .【点睛】本题考查二次函数的性质、二次函数图象上点的坐标特征、待定系数法求二次函数解析式，解题的关键是明确题意，找出所求问题需要的条件，利用数形结合的思想解答问题．6．已知：如图，抛物线y=ax2+bx+c与坐标轴分别交于点A（0，6），B（6，0），C（﹣2，0），点P是线段AB上方抛物线上的一个动点．（1）求抛物线的解析式；（2）当点P运动到什么位置时，△PAB的面积有最大值？（3）过点P作x轴的垂线，交线段AB于点D，再过点P做PE∥x轴交抛物线于点E，连结DE，请问是否存在点P使△PDE为等腰直角三角形？若存在，求出点P的坐标；若不存在，说明理由．【答案】（1）抛物线解析式为y=﹣12x2+2x+6；（2）当t=3时，△PAB的面积有最大值；（3）点P（4，6）．【解析】【分析】（1）利用待定系数法进行求解即可得；（2）作PM⊥OB与点M，交AB于点N，作AG⊥PM，先求出直线AB解析式为y=﹣x+6，设P（t，﹣12t2+2t+6），则N（t，﹣t+6），由S△PAB=S△PAN+S△PBN=12PN•AG+12PN•BM=12PN•OB列出关于t的函数表达式，利用二次函数的性质求解可得；（3）由PH⊥OB知DH∥AO，据此由OA=OB=6得∠BDH=∠BAO=45°，结合∠DPE=90°知若△PDE为等腰直角三角形，则∠EDP=45°，从而得出点E与点A重合，求出y=6时x的值即可得出答案．【详解】（1）∵抛物线过点B（6，0）、C（﹣2，0），∴设抛物线解析式为y=a（x﹣6）（x+2），将点A（0，6）代入，得：﹣12a=6，解得：a=﹣12，所以抛物线解析式为y=﹣12（x﹣6）（x+2）=﹣12x2+2x+6；（2）如图1，过点P作PM⊥OB与点M，交AB于点N，作AG⊥PM于点G，设直线AB 解析式为y=kx+b ，将点A （0，6）、B （6，0）代入，得： 660b k b =⎧⎨+=⎩， 解得：16k b =-⎧⎨=⎩， 则直线AB 解析式为y=﹣x+6，设P （t ，﹣12t 2+2t+6）其中0＜t ＜6， 则N （t ，﹣t+6）， ∴PN=PM ﹣MN=﹣12t 2+2t+6﹣（﹣t+6）=﹣12t 2+2t+6+t ﹣6=﹣12t 2+3t ， ∴S △PAB =S △PAN +S △PBN=12PN•AG+12PN•BM =12PN•（AG+BM ） =12PN•OB =12×（﹣12t 2+3t ）×6 =﹣32t 2+9t =﹣32（t ﹣3）2+272， ∴当t=3时，△PAB 的面积有最大值； （3）如图2，∵PH ⊥OB 于H ， ∴∠DHB=∠AOB=90°， ∴DH ∥AO ， ∵OA=OB=6， ∴∠BDH=∠BAO=45°， ∵PE ∥x 轴、PD ⊥x 轴， ∴∠DPE=90°，若△PDE 为等腰直角三角形， 则∠EDP=45°，∴∠EDP 与∠BDH 互为对顶角，即点E 与点A 重合，则当y=6时，﹣12x 2+2x+6=6， 解得：x=0（舍）或x=4， 即点P （4，6）．【点睛】本题考查了二次函数的综合问题，涉及到待定系数法、二次函数的最值、等腰直角三角形的判定与性质等，熟练掌握和灵活运用待定系数法求函数解析式、二次函数的性质、等腰直角三角形的判定与性质等是解题的关键.7．当今，越来越多的青少年在观看影片《流浪地球》后，更加喜欢同名科幻小说，该小说销量也急剧上升．书店为满足广大顾客需求，订购该科幻小说若干本，每本进价为20元．根据以往经验：当销售单价是25元时，每天的销售量是250本；销售单价每上涨1元，每天的销售量就减少10本，书店要求每本书的利润不低于10元且不高于18元． （1）直接写出书店销售该科幻小说时每天的销售量y （本）与销售单价x （元）之间的函数关系式及自变量的取值范围．（2）书店决定每销售1本该科幻小说，就捐赠(06)a a <≤元给困难职工，每天扣除捐赠后可获得最大利润为1960元，求a 的值．【答案】（1）10500(3038)y x x =-+；（2）2a =． 【解析】 【分析】（1）根据题意列函数关系式即可；（2）设每天扣除捐赠后可获得利润为w 元．根据题意得到w=（x-20-a ）（-10x+500）=-10x 2+（10a+700）x-500a-10000（30≤x≤38）求得对称轴为x ＝35+12a ，且0＜a ≤6，则30＜35+12a ≤38，则当1352x a =+时，w 取得最大值，解方程得到a 1=2，a 2=58，于是得到a=2． 【详解】解：（1）根据题意得，()()2501025105003038y x x x =--=-+； （2）设每天扣除捐赠后可获得利润为w 元．()()()()220105001010700500100003038w x a x x a x a x =---+=-++--对称轴为x ＝35+12a ，且0＜a ≤6，则30＜35+12a ≤38， 则当1352x a =+时，w 取得最大值， ∴1135201035500196022a a x a ⎡⎤⎛⎫⎛⎫+---++= ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦∴122,58a a ==（不合题意舍去），∴2a =． 【点睛】本题考查了二次函数的应用，难度较大，最大销售利润的问题常利用函数的增减性来解答，正确的理解题意，确定变量，建立函数模型．8．如图，已知直线y kx 6=-与抛物线2y ax bx c =++相交于A ，B 两点，且点A （1，－4）为抛物线的顶点，点B 在x 轴上。

人教版初中数学二次函数分类汇编附答案解析一、选择题1．已知二次函数y ＝ax 2+bx +c (a ＞0)经过点M (﹣1，2)和点N (1，﹣2)，则下列说法错误的是( )A ．a +c ＝0B ．无论a 取何值，此二次函数图象与x 轴必有两个交点，且函数图象截x 轴所得的线段长度必大于2C ．当函数在x ＜110时，y 随x 的增大而减小 D ．当﹣1＜m ＜n ＜0时，m +n ＜2a 【答案】C【解析】【分析】根据二次函数的图象和性质对各项进行判断即可．【详解】解：∵函数经过点M (﹣1，2)和点N (1，﹣2)，∴a ﹣b +c ＝2，a +b +c ＝﹣2，∴a +c ＝0，b ＝﹣2，∴A 正确；∵c ＝﹣a ，b ＝﹣2，∴y ＝ax 2﹣2x ﹣a ，∴△＝4+4a 2＞0，∴无论a 为何值，函数图象与x 轴必有两个交点，∵x 1+x 2＝2a，x 1x 2＝﹣1，∴|x 1﹣x 2|＝＞2， ∴B 正确；二次函数y ＝ax 2+bx +c (a ＞0)的对称轴x ＝﹣2b a ＝1a ， 当a ＞0时，不能判定x ＜110时，y 随x 的增大而减小； ∴C 错误；∵﹣1＜m ＜n ＜0，a ＞0，∴m +n ＜0，2a ＞0， ∴m +n ＜2a；∴D 正确，故选：C ．【点睛】本题考查了二次函数的问题，掌握二次函数的图象和性质是解题的关键．2．对于二次函数()21202y ax a x a ⎛⎫=+-< ⎪⎝⎭，下列说法正确的个数是（ ） ①对于任何满足条件的a ，该二次函数的图象都经过点()2,1和()0,0两点；②若该函数图象的对称轴为直线0x x =，则必有001x <<；③当0x ≥时，y 随x 的增大而增大；④若()14,P y ，()()24,0Q m y m +>是函数图象上的两点，如果12y y >总成立，则112a ≤-． A ．1个B ．2个C ．3个D ．4个 【答案】B【解析】【分析】根据二次函数的图象与性质（对称性、增减性）逐个判断即可．【详解】 对于()21202y ax a x a ⎛⎫=+-< ⎪⎝⎭当2x =时，142(2)12y a a =+-=，则二次函数的图象都经过点()2,1当0x =时，0y =，则二次函数的图象都经过点()0,0则说法①正确 此二次函数的对称轴为1212124a x a a-=-=-+ 0a <Q1114a∴-+> 01x ∴>，则说法②错误 由二次函数的性质可知，抛物线的开口向下，当114x a<-+时，y 随x 的增大而增大；当114x a≥-+时，y 随x 的增大而减小因11104a-+>> 则当1014x a <-≤+时，y 随x 的增大而增大；当114x a≥-+时，y 随x 的增大而减小 即说法③错误 0m >Q44m ∴+>由12y y >总成立得，其对称轴1144x a=-+≤ 解得112a ≤-，则说法④正确 综上，说法正确的个数是2个故选：B ．【点睛】 本题考查了二次函数的图象与性质（对称性、增减性），熟练掌握二次函数的图象与性质是解题关键．3．要将抛物线2y x =平移后得到抛物线223y x x =++，下列平移方法正确的是（ ） A ．向左平移1个单位，再向上平移2个单位 B ．向左平移1个单位，再向下平移2个单位 C ．向右平移1个单位，再向上平移2个单位 D ．向右平移1个单位，再向下平移2个单位【答案】A【解析】【分析】原抛物线顶点坐标为（0，0），平移后抛物线顶点坐标为（-1，2），由此确定平移办法．【详解】y=x 2+2x+3=（x+1）2+2，该抛物线的顶点坐标是（-1，2），抛物线y=x 2的顶点坐标是（0，0），则平移的方法可以是：将抛物线y=x 2向左平移1个单位长度，再向上平移2个单位长度． 故选：A ．【点睛】此题考查二次函数图象与几何变换．解题关键是将抛物线的平移问题转化为顶点的平移，寻找平移方法．4．方程2x 3x 10+-=的根可视为函数3y x =+的图象与函数1y x =的图象交点的横坐标，则方程3x 2x 10+-=的实根x 0所在的范围是（ ）A ．010<x <4 B ．011<x <43 C ．011<x <32 D ．01<x <12【答案】C【解析】【分析】首先根据题意推断方程x 3+2x-1=0的实根是函数y=x 2+2与1y x=的图象交点的横坐标，再根据四个选项中x 的取值代入两函数解析式，找出抛物线的图象在反比例函数上方和反比例函数的图象在抛物线的上方两个点即可判定推断方程x 3+2x-1=0的实根x 所在范围．【详解】解：依题意得方程3x 2x 10+-=的实根是函数2y x 2=+与1y x=的图象交点的横坐标，这两个函数的图象如图所示，它们的交点在第一象限．当x=14时，21y x 2216=+=，1y 4x ==，此时抛物线的图象在反比例函数下方； 当x=13时，21229y x =+=，1y 3x ==，此时抛物线的图象在反比例函数下方； 当x=12时，21224y x =+=，1y 2x==，此时抛物线的图象在反比例函数上方； 当x=1时，2y x 23=+=，1y 1x==，此时抛物线的图象在反比例函数上方． ∴方程3x 2x 10+-=的实根x 0所在范围为：011<x <32． 故选C ．【点睛】 此题考查了学生从图象中读取信息的数形结合能力．解决此类识图题，同学们要注意分析其中的“关键点”，还要善于分析各图象的变化趋势．5．如图，二次函数y ＝ax 2+bx +c 的图象过点A （3，0），对称轴为直线x ＝1，给出以下结论：①abc ＜0；②3a +c ＝0；③ax 2+bx ≤a +b ；④若M （﹣0.5，y 1）、N （2.5，y 2）为函数图象上的两点，则y 1＜y 2．其中正确的是（ ）A ．①③④B ．①②3④C ．①②③D ．②③④【答案】C【解析】【分析】 根据二次函数的图象与性质即可求出答案．【详解】解：①由图象可知：a ＜0，c ＞0， 由对称轴可知：2b a -＞0， ∴b ＞0，∴abc ＜0，故①正确；②由对称轴可知：2b a -＝1， ∴b ＝﹣2a ，∵抛物线过点（3，0），∴0＝9a+3b+c ，∴9a ﹣6a+c ＝0，∴3a+c ＝0，故②正确；③当x ＝1时，y 取最大值，y 的最大值为a+b+c ，当x 取全体实数时，ax 2+bx+c≤a+b+c ，即ax 2+bx≤a+b ，故③正确；④（﹣0.5，y 1）关于对称轴x ＝1的对称点为（2.5，y 1）：∴y 1＝y 2，故④错误；故选：C ．【点睛】本题考查二次函数，解题的关键是熟练运用二次函数的图象与性质，本题属于中等题型．6．小明从如图所示的二次函数2y ax bx c =++的图象中，观察得出了下面五条信息：①c ＞0，②abc ＜0，③a -b +c ＞0，④2b ＞4a c ，⑤2a =－2b ，其中正确结论是（ ）．A ．①②④B ．②③④C ．③④⑤D ．①③⑤【答案】C【解析】【分析】 由抛物线的开口方向判断a 的符号，由抛物线与y 轴的交点判断c 的符号，然后根据对称轴及抛物线与x 轴交点情况进行推理，进而对所得结论进行判断．【详解】①由抛物线交y 轴于负半轴，则c<0，故①错误；②由抛物线的开口方向向上可推出a>0；∵对称轴在y 轴右侧，对称轴为x=2b a ->0， 又∵a>0，∴b<0；由抛物线与y 轴的交点在y 轴的负半轴上，∴c<0，故abc>0，故②错误；③结合图象得出x=−1时，对应y 的值在x 轴上方，故y>0，即a−b+c>0，故③正确； ④由抛物线与x 轴有两个交点可以推出b 2−4ac>0，故④正确；⑤由图象可知：对称轴为x=2b a -=12则2a=−2b ，故⑤正确；故正确的有：③④⑤．故选：C【点睛】本题考查了二次函数图象与系数关系，观察图象判断图象开口方向、对称轴所在位置、与x 轴交点个数即可得出二次函数系数满足条件．7．将抛物线y ＝x 2﹣4x +1向左平移至顶点落在y 轴上，如图所示，则两条抛物线.直线y ＝﹣3和x 轴围成的图形的面积S （图中阴影部分）是（ ）A ．5B ．6C ．7D ．8【解析】【分析】B ，C 分别是顶点，A 是抛物线与x 轴的一个交点，连接OC ，AB ，阴影部分的面积就是平行四边形ABCO 的面积.【详解】抛物线y ＝x 2﹣4x +1=(x-2)2-3的顶点坐标C(2.-3), 向左平移至顶点落在y 轴上,此时顶点B(0,-3)，点A 是抛物线与x 轴的一个交点，连接OC ，AB ，如图，阴影部分的面积就是ABCO 的面积，S=2×3=6；故选：B ．【点睛】本题考查二次函数图象的性质，阴影部分的面积；能够将面积进行转化是解题的关键．8．某二次函数图象的顶点为()2,1-，与x 轴交于P 、Q 两点，且6PQ =．若此函数图象通过()1,a 、()3,b 、()1,c -、()3,d -四点，则a 、b 、c 、d 之值何者为正？（ ） A ．aB ．bC ．cD ．d【答案】D【解析】【分析】根据题意可以得到该函数的对称轴，开口方向和与x 轴的交点坐标，从而可以判断a 、b 、c 、d 的正负，本题得以解决．【详解】∵二次函数图象的顶点坐标为（2，-1），此函数图象与x 轴相交于P 、Q 两点，且PQ=6， ∴该函数图象开口向上，对称轴为直线x=2，∴图形与x 轴的交点为（2-3，0）=（-1，0），和（2+3，0）=（5，0），∵此函数图象通过（1，a ）、（3，b ）、（-1，c ）、（-3，d ）四点，∴a ＜0，b ＜0，c=0，d ＞0，故选：D ．此题考查抛物线与x 轴的交点、二次函数的性质、二次函数图象上点的坐标特征，解题的关键是明确题意，利用二次函数的性质解答．9．抛物线2y ax bx c =++（,,a b c 是常数），0a >，顶点坐标为1(,)2m .给出下列结论：①若点1(,)n y 与点23(2)2n y -，在该抛物线上，当12n <时，则12y y <；②关于x 的一元二次方程210ax bx c m -+-+=无实数解，那么（ ）A ．①正确，②正确B ．①正确，②错误C ．①错误，②正确D ．①错误，②错误【答案】A【解析】【分析】①根据二次函数的增减性进行判断便可；②先把顶点坐标代入抛物线的解析式，求得m ，再把m 代入一元二次方程ax 2-bx+c-m+1=0的根的判别式中计算，判断其正负便可判断正误．【详解】解：①∵顶点坐标为1,2m ⎛⎫ ⎪⎝⎭,12n < ∴点（n ，y 1）关于抛物线的对称轴x=12的对称点为（1-n ，y 1）， ∴点（1-n ，y 1）与2322n y ⎛⎫- ⎪⎝⎭，在该抛物线的对称轴的右侧图像上, 31(1)2022n n n ⎛⎫---=-< ⎪⎝⎭Q 3122n n ∴-<- ∵a ＞0，∴当x ＞12时，y 随x 的增大而增大， ∴y 1＜y 2，故此小题结论正确； ②把1,2m ⎛⎫ ⎪⎝⎭代入y=ax 2+bx+c 中，得1142m a b c =++, ∴一元二次方程ax 2-bx+c-m+1=0中， △=b 2-4ac+4am-4a 2211444()4042b ac a a b c a a b a ⎛⎫=-+++-=+-< ⎪⎝⎭ ∴一元二次方程ax 2-bx+c-m+1=0无实数解，故此小题正确；故选A ．本题主要考查了二次函数图象与二次函数的系数的关系，第①小题，关键是通过抛物线的对称性把两点坐标变换到对称轴的一边来，再通过二次函数的增减性进行比较，第②小题关键是判断一元二次方程根的判别式的正负．10．如图，已知点A（4，0），O为坐标原点，P是线段OA上任意一点（不含端点O，A），过P、O两点的二次函数y1和过P、A两点的二次函数y2的图象开口均向下，它们的顶点分别为B、C，射线OB与AC相交于点D．当OD=AD=3时，这两个二次函数的最大值之和等于（）A．5B．453C．3 D．4【答案】A【解析】【分析】【详解】过B作BF⊥OA于F，过D作DE⊥OA于E，过C作CM⊥OA于M，∵BF⊥OA，DE⊥OA，CM⊥OA，∴BF∥DE∥CM．∵OD=AD=3，DE⊥OA，∴OE=EA=12OA=2．由勾股定理得：5设P（2x，0），根据二次函数的对称性得出OF=PF=x，∵BF∥DE∥CM，∴△OBF∽△ODE，△ACM∽△ADE．∴BF OF CM AM DE OE DE AE ==，，即x 2x 2255-==，，解得：()52x 5BF ?x CM 22-==，． ∴BF+CM=5．故选A ．11．已知二次函数223(0)y ax ax a a =--≠，关于此函数的图象及性质，下列结论中不一定成立的是( )A ．该图象的顶点坐标为()1,4a -B ．该图象与x 轴的交点为()()1,0,3,0-C ．若该图象经过点()2,5-，则一定经过点()4,5D ．当1x >时，y 随x 的增大而增大【答案】D【解析】【分析】根据二次函数的图象与性质即可求出答案．【详解】解：y=a （x 2-2x-3）=a （x-3）（x+1）令y=0，∴x=3或x=-1，∴抛物线与x 轴的交点坐标为（3，0）与（-1，0），故B 成立；∴抛物线的对称轴为：x=1，令x=1代入y=ax 2-2ax-3a ，∴y=a-2a-3a=-4a ，∴顶点坐标为（1，-4a ），故A 成立；由于点（-2，5）与（4，5）关于直线x=1对称，∴若该图象经过点（-2，5），则一定经过点（4，5），故C 成立；当x ＞1，a ＞0时，y 随着x 的增大而增大，当x ＞1，a ＜0时，y 随着x 的增大而减少，故D 不一定成立；故选：D ．【点睛】本题考查二次函数，解题的关键是熟练运用二次函数的图象与性质，本题属于基础题型．12．已知抛物线y ＝x 2+2x ﹣m ﹣1与x 轴没有交点，则函数y ＝的大致图象是（ ）A．B．C．D．【答案】B【解析】【分析】由题意可求m＜﹣2，即可求解．【详解】∵抛物线y＝x2+2x﹣m﹣1与x轴没有交点，∴△＝4﹣4（﹣m﹣1）＜0∴m＜﹣2∴函数y＝的图象在第二、第四象限，故选B．【点睛】本题考查了反比例函数的图象，二次函数性质，求m的取值范围是本题的关键．13．在平面直角坐标系内，已知点A（﹣1，0），点B（1，1）都在直线1122y x=+上，若抛物线y＝ax2﹣x+1（a≠0）与线段AB有两个不同的交点，则a的取值范围是（）A．a≤﹣2 B．a＜98C．1≤a＜98或a≤﹣2 D．﹣2≤a＜98【答案】C 【解析】分a ＞0，a ＜0两种情况讨论，根据题意列出不等式组，可求a 的取值范围．【详解】∵抛物线y ＝ax 2﹣x +1（a ≠0）与线段AB 有两个不同的交点， ∴令1122x +＝ax 2﹣x +1，则2ax 2﹣3x +1＝0 ∴△＝9﹣8a ＞0 ∴a ＜98①当a ＜0时，110111a a ++≤⎧⎨-+≤⎩ 解得：a ≤﹣2∴a ≤﹣2 ②当a ＞0时，110111a a ++≥⎧⎨-+≥⎩解得：a ≥1∴1≤a ＜98综上所述：1≤a ＜98或a ≤﹣2 故选：C ．【点睛】本题考查二次函数图象与系数的关系，一次函数图象上点的坐标特征，二次函数图象点的坐标特征，利用分类讨论思想解决问题是本题的关键．14．如图，已知将抛物线21y x =-沿x 轴向上翻折与所得抛物线围成一个封闭区域（包括边界），在这个区域内有5个整点（点M 满足横、纵坐标都为整数，则把点M 叫做“整点”）.现将抛物线()()2120y a x a =++<沿x 轴向下翻折，所得抛物线与原抛物线所围成的封闭区域内（包括边界）恰有11个整点，则a 的取值范围是（ ）A ．1a ≤-B ．12a ≤-C ．112a -<≤D ．112a -≤<- 【答案】D【分析】画出图象，利用图象可得m 的取值范围【详解】解：∵ ()()2120y a x a =++<∴该抛物线开口向下，顶点(-1，2)，对称轴是直线x=-1.∴点(-1,2)、点(-1，1)、点(-1, 0)、点(-1,-1)、点(-1，-2)符合题意，此时x 轴.上的点(-2, 0)、(0, 0)也符合题意，将(0，1)代入()()2120y a x a =++<得到1=a+2.解得a=-1.将(1, 0)代入()()2120y a x a =++<得到0= 4a+2.解得a=1-2∵有11个整点，∴点(0，-1)、点(-2, -1)、点(-2,1)、点(0，1)也必须符合题意. 综上可知:当1-1a<-2≤ 时，点(-1，2)、点(-1，1)、点(-1, 0)、点(-1，-1)、点(-1，-2)、点(-2, 0)、(0，0)、点(0，-1)、点(-2，-1)、点(-2，1)、点(0, 1)，共有11个整点符合题意, 故选: D.【点睛】 本题考查了二次函数图象与系数的关系，抛物线与x 轴的交点的求法，利用图象解决问题是本题的关键.15．若A （－4，1y ），B （－3，2y ），C （1，3y ）为二次函数y =x 2+4x －m 的图象上的三点，则1y ，2y ，3y 的大小关系是（ ）A ．1y ＜2y ＜3yB ．3y ＜1y ＜2yC ．2y ＜1y ＜3yD ．1y ＜3y ＜2y【答案】C【分析】分别将点的坐标代入二次函数解析式，然后进行判断即可．【详解】解：y 1=（-4）2+4×（-4）m -=16-16m - =m -，y 2=（-3）2+4×（-3）m - =9-12m - =3m --，y 3=12+4×m - 1=1+4m - =5m -，∵-3m -＜m -＜5m -，∴y 2＜y 1＜y 3．故选：C.【点睛】本题考查了二次函数图象上点的坐标特征，解题的关键在于三个函数值的大小不受m 的影响．16．函数2y ax b y ax bx c =+=++和在同一直角坐标系内的图象大致是（ ） A ． B ． C ． D ．【答案】C【解析】【分析】根据a 、b 的符号，针对二次函数、一次函数的图象位置，开口方向，分类讨论，逐一排除．【详解】当a ＞0时，二次函数的图象开口向上，一次函数的图象经过一、三或一、二、三或一、三、四象限，故A 、D 不正确；由B 、C 中二次函数的图象可知，对称轴x=-2b a＞0，且a ＞0，则b ＜0， 但B 中，一次函数a ＞0，b ＞0，排除B ．故选C ．17．已知抛物线y ＝x 2+（2a +1）x +a 2﹣a ，则抛物线的顶点不可能在（ ）A ．第一象限B ．第二象限C ．第三象限D ．第四象限【答案】D【解析】【分析】求得顶点坐标，得出顶点的横坐标和纵坐标的关系式，即可求得．【详解】抛物线y＝x2+（2a+1）x+a2﹣a的顶点的横坐标为：x＝﹣212a+＝﹣a﹣12，纵坐标为：y＝()()224214a a a--+＝﹣2a﹣14，∴抛物线的顶点横坐标和纵坐标的关系式为：y＝2x+34，∴抛物线的顶点经过一二三象限，不经过第四象限，故选：D．【点睛】本题考查了二次函数的性质，得到顶点的横纵坐标的关系式是解题的关键．18．已知抛物线y=x2+2x上三点A（﹣5，y1），B（2.5，y2），C（12，y3），则y1，y2，y3满足的关系式为（）A．y1＜y2＜y3 B．y3＜y2＜y1 C．y2＜y1＜y3 D．y3＜y1＜y2【答案】C【解析】【分析】首先求出抛物线y=x2+2x的对称轴，对称轴为直线x=-1；然后根据A、B、C的横坐标与对称轴的位置，接着利用抛物线的增减性质即可求解；由B离对称轴最近，A次之，C最远，则对应y的值大小可确定.【详解】∵抛物线y=x2+2x，∴x=-1，而A（-5，y1），B（2.5，y2），C（12，y3），∴B离对称轴最近，A次之，C最远，∴y2＜y1＜y3．故选:C．【点睛】本题考查了二次函数的图象和性质，二次函数图象上点的坐标特征等知识点，能熟记二次函数的性质是解此题的关键．19．在同一直角坐标系中，反比例函数图像与二次函数图像的交点的个数至少有() A．0B．1C．2D．3【答案】B【解析】【分析】根据二次函数和反比例函数的图象位置，画出图象，直接判断交点个数．【详解】若二次函数的图象在第三、四象限，开口向下，顶点在原点，y 轴是对称轴；反比例函数的图象在第一，三象限，故两个函数的交点只有一个，在第三象限．同理，若二次函数的图象在第三、四象限，开口向下，顶点在原点，y 轴是对称轴；反比例函数的图象在第二，四象限，故两个函数的交点只有一个，在第四象限．故答案为：B ．【点睛】本题考查了二次函数和反比例函数的图象问题，掌握二次函数和反比例函数的图象性质是解题的关键．20．平移抛物线2:L y x =得到抛物线L '，使得抛物线L '的顶点关于原点对称的点仍在抛物线L '上，下列的平移中，不能得到满足条件的抛物线L '的是（ ）A ．向右平移1个单位，再向下平移2个单位B ．向左平移1个单位，再向下平移2个单位C ．向左平移32个单位，再向下平移92个单位 D ．向左平移3个单位，再向下平移9个单位【答案】D【解析】【分析】通过各个选项的平移分别得到相应的函数关系式，再判断原点是否在该抛物线上即可．【详解】解：由A 选项可得L '为：2(1)2y x =--，则顶点为（1，-2），顶点（1，-2）关于原点的对称点为（-1，2），当x ＝-1时，y ＝2，则对称点在该函数图像上，故A 选项不符合题意；由B 选项可得L '为：2(1)2y x =+-，则顶点为（-1，-2），顶点（-1，-2）关于原点的对称点为（1，2），当x ＝1时，y ＝2，则对称点在该函数图像上，故B 选项不符合题意；由C 选项可得L '为：239()22y x =+-，则顶点为（-32，-92），顶点（-32，-92）关于原点的对称点为（32，92）， 当x ＝32时，y ＝92，则对称点在该函数图像上，故C 选项不符合题意； 由D 选项可得L '为：2(3)9y x =+-，则顶点为（-3，-9），顶点（-3，-9）关于原点的对称点为（3，9），当x ＝3时，y ＝27≠9，则对称点不在该函数图像上，故D 选项符合题意；故选：D ．【点睛】本题考查了二次函数图像的平移，熟练掌握平移的规律“左加右减，上加下减”是解决本题的关键．。

人教版初中数学二次函数分类汇编及答案一、选择题1．如图，ABC ∆为等边三角形，点P 从A 出发，沿A B C A →→→作匀速运动，则线段AP 的长度y 与运动时间x 之间的函数关系大致是（ ）A ．B ．C ．D ．【答案】B 【解析】 【分析】根据题意可知点P 从点A 运动到点B 时以及从点C 运动到点A 时是一条线段，故可排除选项C 与D ；点P 从点B 运动到点C 时，y 是x 的二次函数，并且有最小值，故选项B 符合题意，选项A 不合题意． 【详解】根据题意得，点P 从点A 运动到点B 时以及从点C 运动到点A 时是一条线段，故选项C 与选项D 不合题意；点P 从点B 运动到点C 时，y 是x 的二次函数，并且有最小值， ∴选项B 符合题意，选项A 不合题意． 故选B ． 【点睛】本题考查了动点问题的函数图象：通过分类讨论，利用三角形面积公式得到y 与x 的函数关系，然后根据二次函数和一次函数图象与性质解决问题．2．一列自然数0，1，2，3，…，100．依次将该列数中的每一个数平方后除以100，得到一列新数．则下列结论正确的是（ ） A ．原数与对应新数的差不可能等于零B ．原数与对应新数的差，随着原数的增大而增大C ．当原数与对应新数的差等于21时，原数等于30D ．当原数取50时，原数与对应新数的差最大 【答案】D【解析】 【分析】设出原数，表示出新数，利用解方程和函数性质即可求解． 【详解】解：设原数为m ，则新数为21100m ，设新数与原数的差为y则2211100100y m m m m =-=-+， 易得，当m ＝0时，y ＝0，则A 错误∵10100-< 当1m 50122100b a ﹣﹣﹣===⎛⎫⨯ ⎪⎝⎭时，y 有最大值．则B 错误，D 正确． 当y ＝21时，21100m m -+＝21 解得1m ＝30，2m ＝70，则C 错误． 故答案选：D ． 【点睛】本题以规律探究为背景，综合考查二次函数性质和解一元二次方程，解题时要注意将数字规律转化为数学符号．3．已知，二次函数y=ax 2+bx+a 2+b （a≠0）的图象为下列图象之一，则a 的值为（ ）A ．-1B ．1C ．-3D ．-4【答案】A 【解析】 【分析】分别对图形进行讨论：若二次函数的图形为第一个，则b=0，其顶点坐标为(0，a 2)，与图形中的顶点坐标不符；若二次函数的图形为第二个，则b=0，根据顶点坐标有a 2=3，由抛物线与x 的交点坐标得到x 2=-a ，所以a=-4，它们相矛盾；若二次函数的图形为第三个，把点(-1，0)代入解析式得到a-b+a 2+b=0，解得a=-1；若二次函数的图形为第四个，把(-2，0)和(0，0)分别代入解析式可计算出a 的值． 【详解】解：若二次函数的图形为第一个，对称轴为y 轴，则b=0，y=ax 2+a 2，其顶点坐标为(0，a 2)，而a 2>0，所以二次函数的图形不能为第一个；若二次函数的图形为第二个，对称轴为y 轴，则b=0，y=ax 2+a 2，a 2=3，而当y=0时，x 2=−a ，所以−a=4，a=−4，所以二次函数的图形不能为第二个；若二次函数的图形为第三个，令x=−1，y=0，则a−b+a 2+b=0，所以a=−1； 若二次函数的图形为第四个，令x=0，y=0，则a 2+b=0①；令x=−2，y=0，则4a−2b+a 2+b=0②，由①②得a=−2，这与图象开口向上不符合，所以二次函数的图形不能为第四个. 故选A. 【点睛】本题考查了二次函数y=ax 2+bx+c(a≠0)的图象与系数的关系：a ＞0，开口向上；a ＜0，开口向下；抛物线的对称轴为直线x=-；顶点坐标为(-，)；也考查了点在抛物线上则点的坐标满足抛物线的解析式.4．已知抛物线2y ax bx c =++与x 轴的一个交点坐标为(4,0)，其部分图象如图所示，下列结论：①抛物线一定过原点；②方程()200++=≠ax bx c a 的解为0x =或4；③0a b c -+<；④当04x <<时，20ax bx c ++<；⑤当2x <时，y 随x 增大而增大．其中结论正确的个数有（ ）A ．1B ．2C ．3D ．4【答案】D 【解析】 【分析】根据题意，求得,,a b c ，根据二次函数的图像和性质，结合选项进行逐一分析，即可判断. 【详解】 由题可知22ba-=，与x 轴的一个交点坐标为(4,0)，则另一个交点坐标为()0,0， 故可得1640a b c ++=，0c =， 故可得4,0a b c -== ①因为0c =，故①正确；②因为二次函数过点()()0,0,4,0，故②正确；③当1x =-时，函数值为0a b c -+<，故③正确； ④由图可知，当04x <<时，0y <，故④正确； ⑤由图可知，当2x <时，y 随x 增大而减小，故⑤错误； 故选：D. 【点睛】本题考查二次函数的图像和性质，涉及二次函数的增减性，属综合中档题.5．如图是抛物线y ＝ax 2+bx +c （a ≠0）的部分图象，其顶点坐标为（1，m ），且与x 铀的一个交点在点（3，0）和（4，0）之间，则下列结论：①abc ＞0；②a ﹣b +c ＞0；③b 2＝4a （c ﹣m ）；④一元二次方程ax 2+bx +c ＝m +1有两个不相等的实数根，其中正确结论的个数是（ ）A ．1B ．2C ．3D ．4【答案】C 【解析】 【分析】根据抛物线的开口方向和与坐标轴的交点及对称轴可判别a ，b ，c 的正负；根据抛物线的对称轴位置可判别在x 轴上另一个交点；根据抛物线与直线y=m 的交点可判定方程的解． 【详解】∵函数的图象开口向上，与y 轴交于负半轴 ∴a>0,c<0∵抛物线的对称轴为直线x=－2b a=1 ∴b<0∴abc ＞0；①正确；∵抛物线与x 轴的一个交点在点（3，0）和（4，0）之间，而抛物线的对称轴为直线x=1，∴抛物线与x 轴的另一个交点在点（-2，0）和（-1，0）之间． ∴当x=-1时，y<0，即a-b+c<0，所以②不正确； ∵抛物线的顶点坐标为（1，m ）， ∴244ac b a- =m ，∴b 2=4ac-4am=4a （c-m ），所以③正确； ∵抛物线与直线y=m 有一个公共点， ∴抛物线与直线y=m+1有2个公共点，∴一元二次方程ax 2+bx+c=m+1有两个不相等的实数根，所以④正确． 故选:C ． 【点睛】考核知识点：抛物线与一元二次方程．理解二次函数性质，弄清抛物线与一元二次方程的关系是关键．6．方程2x 3x 10+-=的根可视为函数3y x =+的图象与函数1y x=的图象交点的横坐标，则方程3x 2x 10+-=的实根x 0所在的范围是（ ） A ．010<x <4B ．011<x <43C ．011<x <32D ．01<x <12【答案】C 【解析】 【分析】首先根据题意推断方程x 3+2x-1=0的实根是函数y=x 2+2与1y x=的图象交点的横坐标，再根据四个选项中x 的取值代入两函数解析式，找出抛物线的图象在反比例函数上方和反比例函数的图象在抛物线的上方两个点即可判定推断方程x 3+2x-1=0的实根x 所在范围． 【详解】解：依题意得方程3x 2x 10+-=的实根是函数2y x 2=+与1y x=的图象交点的横坐标，这两个函数的图象如图所示，它们的交点在第一象限．当x=14时，21y x 2216=+=，1y 4x ==，此时抛物线的图象在反比例函数下方； 当x=13时，21229y x =+=，1y 3x==，此时抛物线的图象在反比例函数下方； 当x=12时，21224y x =+=，1y 2x==，此时抛物线的图象在反比例函数上方； 当x=1时，2y x 23=+=，1y 1x==，此时抛物线的图象在反比例函数上方．∴方程3x 2x 10+-=的实根x 0所在范围为：011<x <32． 故选C ． 【点睛】此题考查了学生从图象中读取信息的数形结合能力．解决此类识图题，同学们要注意分析其中的“关键点”，还要善于分析各图象的变化趋势．7．已知二次函数y ＝ax 2+bx +c （a ≠0）的图象如图所示，则下列结论：（1）4a +2b +c ＜0；（2）方程ax 2+bx +c ＝0两根都大于零；（3）y 随x 的增大而增大；（4）一次函数y ＝x +bc 的图象一定不过第二象限．其中正确的个数是（ ）A ．1个B ．2个C ．3个D ．4个【答案】C 【解析】 【分析】由图可知，x=2时函数值小于0，故（1）正确，函数与x 轴的交点为x=1.x=3，都大于0，故（2）正确 ，由图像知（3）错误，由图象开口向上，a ＞0，与y 轴交于正半轴，c ＞0，对称轴x=﹣＝1，故b ＜0，bc ＜0，即可判断一次函数y ＝x +bc 的图象.【详解】①由x ＝2时，y ＝4a +2b +c ，由图象知：y ＝4a +2b +c ＜0，故正确； ②方程ax 2+bx +c ＝0两根分别为1，3，都大于0，故正确； ③当x ＜2时，由图象知：y 随x 的增大而减小，故错误； ④由图象开口向上，a ＞0，与y 轴交于正半轴，c ＞0，x=﹣＝1＞0，∴b ＜0，∴bc ＜0，∴一次函数y ＝x +bc 的图象一定过第一、三、四象限，故正确； 故正确的共有3个， 故选：C ． 【点睛】此题主要考查二次函数的图像，解题的关键是熟知各系数所代表的含义.8．二次函数y ＝x 2+bx 的对称轴为直线x ＝2，若关于x 的一元二次方程x 2+bx ﹣t ＝0（t 为实数）在﹣1＜x ＜4的范围内有解，则t 的取值范围是（ ） A ．0＜t ＜5 B ．﹣4≤t ＜5C ．﹣4≤t ＜0D ．t ≥﹣4【答案】B 【解析】【分析】先求出b ，确定二次函数解析式，关于x 的一元二次方程x 2+bx ﹣t ＝0的解可以看成二次函数y ＝x 2﹣4x 与直线y ＝t 的交点，﹣1＜x ＜4时﹣4≤y ＜5，进而求解； 【详解】解：∵对称轴为直线x ＝2， ∴b ＝﹣4， ∴y ＝x 2﹣4x ，关于x 的一元二次方程x 2+bx ﹣t ＝0的解可以看成二次函数y ＝x 2﹣4x 与直线y ＝t 的交点， ∵﹣1＜x ＜4，∴二次函数y 的取值为﹣4≤y ＜5， ∴﹣4≤t ＜5； 故选：B ． 【点睛】本题考查二次函数图象的性质，一元二次方程的解；将一元二次方程的解转换为二次函数与直线交点问题，数形结合的解决问题是解题的关键．9．若平面直角坐标系内的点M 满足横、纵坐标都为整数，则把点M 叫做“整点”．例如：P （1，0）、Q （2，﹣2）都是“整点”．抛物线y ＝mx 2﹣4mx +4m ﹣2（m ＞0）与x 轴交于点A 、B 两点，若该抛物线在A 、B 之间的部分与线段AB 所围成的区域（包括边界）恰有七个整点，则m 的取值范围是（ ）A ．12≤m ＜1 B ．12＜m ≤1 C ．1＜m ≤2 D ．1＜m ＜2【答案】B 【解析】 【分析】画出图象，利用图象可得m 的取值范围【详解】∵y ＝mx 2﹣4mx +4m ﹣2＝m （x ﹣2）2﹣2且m ＞0，∴该抛物线开口向上，顶点坐标为（2，﹣2），对称轴是直线x ＝2． 由此可知点（2，0）、点（2，﹣1）、顶点（2，﹣2）符合题意．①当该抛物线经过点（1，﹣1）和（3，﹣1）时（如答案图1），这两个点符合题意． 将（1，﹣1）代入y ＝mx 2﹣4mx +4m ﹣2得到﹣1＝m ﹣4m +4m ﹣2．解得m ＝1． 此时抛物线解析式为y ＝x 2﹣4x +2．由y ＝0得x 2﹣4x +2＝0．解得12120.62 3.42x x ==-≈+≈，． ∴x 轴上的点（1，0）、（2，0）、（3，0）符合题意．则当m ＝1时，恰好有 （1，0）、（2，0）、（3，0）、（1，﹣1）、（3，﹣1）、（2，﹣1）、（2，﹣2）这7个整点符合题意．∴m ≤1．【注：m 的值越大，抛物线的开口越小，m 的值越小，抛物线的开口越大】答案图1（m ＝1时） 答案图2（ m ＝时）②当该抛物线经过点（0，0）和点（4，0）时（如答案图2），这两个点符合题意． 此时x 轴上的点 （1，0）、（2，0）、（3，0）也符合题意． 将（0，0）代入y ＝mx 2﹣4mx +4m ﹣2得到0＝0﹣4m +0﹣2．解得m ＝12． 此时抛物线解析式为y ＝12x 2﹣2x ． 当x ＝1时，得13121122y =⨯-⨯=-<-．∴点（1，﹣1）符合题意．当x ＝3时，得13923122y =⨯-⨯=-<-.∴点（3，﹣1）符合题意． 综上可知：当m ＝12时，点（0，0）、（1，0）、（2，0）、（3，0）、（4，0）、（1，﹣1）、（3，﹣1）、（2，﹣2）、（2，﹣1）都符合题意，共有9个整点符合题意， ∴m ＝12不符合题． ∴m ＞12． 综合①②可得：当12＜m ≤1时，该函数的图象与x 轴所围成的区域（含边界）内有七个整点， 故选：B ． 【点睛】考查二次函数图象与系数的关系，抛物线与x 轴的交点，画出图象，数形结合是解题的关键.10．抛物线2y ax bx c =++（,,a b c 是常数），0a >，顶点坐标为1(,)2m .给出下列结论：①若点1(,)n y 与点23(2)2n y -，在该抛物线上，当12n <时，则12y y <；②关于x的一元二次方程210ax bx c m -+-+=无实数解，那么（ ）A ．①正确，②正确B ．①正确，②错误C ．①错误，②正确D ．①错误，②错误 【答案】A 【解析】 【分析】①根据二次函数的增减性进行判断便可；②先把顶点坐标代入抛物线的解析式，求得m ，再把m 代入一元二次方程ax 2-bx+c-m+1=0的根的判别式中计算，判断其正负便可判断正误． 【详解】解：①∵顶点坐标为1,2m ⎛⎫⎪⎝⎭,12n <∴点（n ，y 1）关于抛物线的对称轴x=12的对称点为（1-n ，y 1）， ∴点（1-n ，y 1）与2322n y ⎛⎫-⎪⎝⎭，在该抛物线的对称轴的右侧图像上, 31(1)2022n n n ⎛⎫---=-< ⎪⎝⎭Q3122n n ∴-<- ∵a ＞0，∴当x ＞12时，y 随x 的增大而增大， ∴y 1＜y 2，故此小题结论正确；②把1,2m ⎛⎫⎪⎝⎭代入y=ax 2+bx+c 中，得1142m a b c =++,∴一元二次方程ax 2-bx+c-m+1=0中， △=b 2-4ac+4am-4a 2211444()4042b ac a a b c a a b a ⎛⎫=-+++-=+-<⎪⎝⎭∴一元二次方程ax 2-bx+c-m+1=0无实数解，故此小题正确； 故选A ． 【点睛】本题主要考查了二次函数图象与二次函数的系数的关系，第①小题，关键是通过抛物线的对称性把两点坐标变换到对称轴的一边来，再通过二次函数的增减性进行比较，第②小题关键是判断一元二次方程根的判别式的正负．11．二次函数y=ax 2+bx+c （a≠0）的部分图象如图所示，图象过点（﹣1，0），对称轴为直线x=2，下列结论：（1）4a+b=0；（2）9a+c ＞﹣3b ；（3）7a ﹣3b+2c ＞0；（4）若点A（﹣3，y 1）、点B （﹣12，y 2）、点C （7，y 3）在该函数图象上，则y 1＜y 3＜y 2；（5）若方程a （x+1）（x ﹣5）=﹣3的两根为x 1和x 2，且x 1＜x 2，则x 1＜﹣1＜5＜x 2．其中正确的结论有（ ）A ．2个B ．3个C ．4个D ．5个【答案】B 【解析】根据题意和函数的图像，可知抛物线的对称轴为直线x=-2ba=2，即b=-4a ，变形为4a+b=0，所以（1）正确；由x=-3时，y ＞0，可得9a+3b+c ＞0，可得9a+c ＞-3c ，故（2）正确；因为抛物线与x 轴的一个交点为(-1,0)可知a-b+c=0，而由对称轴知b=-4a ，可得a+4a+c=0，即c=-5a.代入可得7a ﹣3b+2c=7a+12a-5a=14a ，由函数的图像开口向下，可知a ＜0，因此7a ﹣3b+2c ＜0，故（3）不正确；根据图像可知当x ＜2时，y 随x 增大而增大，当x ＞2时，y 随x 增大而减小，可知若点A （﹣3，y 1）、点B （﹣12，y 2）、点C （7，y 3）在该函数图象上，则y 1=y 3＜y 2，故（4）不正确；根据函数的对称性可知函数与x 轴的另一交点坐标为（5，0），所以若方程a （x+1）（x ﹣5）=﹣3的两根为x 1和x 2，且x 1＜x 2，则x 1＜﹣1＜x 2，故（5）正确． 正确的共有3个. 故选B.点睛：本题考查了二次函数图象与系数的关系：二次函数y=ax 2+bx+c （a≠0），二次项系数a 决定抛物线的开口方向和大小，当a ＞0时，抛物线向上开口；当a ＜0时，抛物线向下开口；一次项系数b 和二次项系数a 共同决定对称轴的位置，当a 与b 同号时（即ab ＞0），对称轴在y 轴左； 当a 与b 异号时（即ab ＜0），对称轴在y 轴右；常数项c 决定抛物线与y 轴交点． 抛物线与y 轴交于（0，c ）；抛物线与x 轴交点个数由△决定，△=b 2﹣4ac ＞0时，抛物线与x 轴有2个交点；△=b 2﹣4ac=0时，抛物线与x 轴有1个交点；△=b 2﹣4ac ＜0时，抛物线与x 轴没有交点．12．如图，已知将抛物线21y x =-沿x 轴向上翻折与所得抛物线围成一个封闭区域（包括边界），在这个区域内有5个整点（点M 满足横、纵坐标都为整数，则把点M 叫做“整点”）.现将抛物线()()2120y a x a =++<沿x 轴向下翻折，所得抛物线与原抛物线所围成的封闭区域内（包括边界）恰有11个整点，则a 的取值范围是（ ）A ．1a ≤-B ．12a ≤-C ．112a -<≤D ．112a -≤<- 【答案】D【解析】【分析】 画出图象，利用图象可得m 的取值范围【详解】解：∵ ()()2120y a x a =++<∴该抛物线开口向下，顶点(-1，2)，对称轴是直线x=-1.∴点(-1,2)、点(-1，1)、点(-1, 0)、点(-1,-1)、点(-1，-2)符合题意，此时x 轴.上的点(-2, 0)、(0, 0)也符合题意，将(0，1)代入()()2120y a x a =++<得到1=a+2.解得a=-1.将(1, 0)代入()()2120y a x a =++<得到0= 4a+2.解得a=1-2∵有11个整点，∴点(0，-1)、点(-2, -1)、点(-2,1)、点(0，1)也必须符合题意. 综上可知:当1-1a<-2≤ 时，点(-1，2)、点(-1，1)、点(-1, 0)、点(-1，-1)、点(-1，-2)、点(-2, 0)、(0，0)、点(0，-1)、点(-2，-1)、点(-2，1)、点(0, 1)，共有11个整点符合题意,故选: D.【点睛】本题考查了二次函数图象与系数的关系，抛物线与x 轴的交点的求法，利用图象解决问题是本题的关键.13．二次函数2y ax bx c =++（,,a b c 是常数，0a ≠）的自变量x 与函数值y 的部分对应值如下表：且当12x =-时，与其对应的函数值0y >．有下列结论：①0abc >；②2-和3是关于x 的方程2ax bx c t ++=的两个根；③0m <203n +<．其中，正确结论的个数是（ ） A ．0B ．1C ．2D ．3【答案】C【解析】【分析】 首先确定对称轴，然后根据二次函数的图像和性质逐一进行分析即可求解．【详解】∵由表格可知当x=0和x=1时的函数值相等都为-2∴抛物线的对称轴是：x=-2b a =12； ∴a 、b 异号，且b=-a ；∵当x=0时y=c=-2∴c 0<∴abc >0，故①正确；∵根据抛物线的对称性可得当x=-2和x=3时的函数值相等都为t∴2-和3是关于x 的方程2ax bx c t ++=的两个根；故②正确；∵b=-a ，c=-2∴二次函数解析式：2-a -2=y ax x ∵当12x =-时，与其对应的函数值0y >． ∴3204a ->，∴a 83>； ∵当x=-1和x=2时的函数值分别为m 和n ，∴m=n=2a-2，∴m+n=4a-4203>；故③错误 故选：C ．【点睛】 本题考查了二次函数的综合题型，主要利用了二次函数图象与系数的关系，二次函数的对称性，二次函数与一元二次方程等知识点，要会利用数形结合的思想，根据给定自变量x 与函数值y 的值结合二次函数的性质逐条分析给定的结论是关键．14．若A （－4，1y ），B （－3，2y ），C （1，3y ）为二次函数y =x 2+4x －m 的图象上的三点，则1y ，2y ，3y 的大小关系是（ ）A ．1y ＜2y ＜3yB ．3y ＜1y ＜2yC ．2y ＜1y ＜3yD ．1y ＜3y ＜2y【答案】C【解析】【分析】分别将点的坐标代入二次函数解析式，然后进行判断即可．【详解】解：y 1=（-4）2+4×（-4）m -=16-16m - =m -，y 2=（-3）2+4×（-3）m - =9-12m - =3m --，y 3=12+4×m - 1=1+4m - =5m -，∵-3m -＜m -＜5m -，∴y 2＜y 1＜y 3．故选：C.【点睛】本题考查了二次函数图象上点的坐标特征，解题的关键在于三个函数值的大小不受m 的影响．15．二次函数y=﹣x 2+mx 的图象如图，对称轴为直线x=2，若关于x 的一元二次方程﹣x 2+mx ﹣t=0（t 为实数）在1＜x ＜5的范围内有解，则t 的取值范围是（ ）A ．t ＞﹣5B ．﹣5＜t ＜3C ．3＜t≤4D ．﹣5＜t≤4【答案】D【解析】【分析】 先根据对称轴x=2求得m 的值，然后求得x=1和x=5时y 的值，最后根据图形的特点，得出直线y=t 在直线y=﹣5和直线y=4之间包括直线y=4．【详解】∵抛物线的对称轴为x ＝2， ∴22m -=-，m=4 如图，关于x 的一元二次方程﹣x 2+mx ﹣t=0的解就是抛物线y=﹣x 2+mx 与直线y=t 的交点的横坐标当x=1时，y=3，当x=5时，y=﹣5，由图象可知关于x 的一元二次方程﹣x 2+mx ﹣t=0（t 为实数）在1＜x ＜5的范围内有解， 则直线y=t 在直线y=﹣5和直线y=4之间包括直线y=4，∴﹣5＜t≤4．故选：D ．【点睛】本题考查二次函数与一元二次方程的关系，方程有解，反映在图象上即图象与x 轴(或某直线)有交点．16．在同一平面直角坐标系中，函数y=ax 2+bx 与y=bx+a 的图象可能是（ ）A ．B ．C ．D ．【答案】C【解析】试题解析：A 、对于直线y=bx+a 来说，由图象可以判断，a ＞0，b ＞0；而对于抛物线y=ax 2+bx 来说，对称轴x=﹣2b a＜0，应在y 轴的左侧，故不合题意，图形错误． B 、对于直线y=bx+a 来说，由图象可以判断，a ＜0，b ＜0；而对于抛物线y=ax 2+bx 来说，图象应开口向下，故不合题意，图形错误．C 、对于直线y=bx+a 来说，由图象可以判断，a ＜0，b ＞0；而对于抛物线y=ax 2+bx 来说，图象开口向下，对称轴x=﹣2b a位于y 轴的右侧，故符合题意， D 、对于直线y=bx+a 来说，由图象可以判断，a ＞0，b ＞0；而对于抛物线y=ax 2+bx 来说，图象开口向下，a ＜0，故不合题意，图形错误．故选C ．考点：二次函数的图象；一次函数的图象．17．在同一直角坐标系中，反比例函数图像与二次函数图像的交点的个数至少有( ) A ．0B ．1C ．2D ．3【答案】B【解析】【分析】根据二次函数和反比例函数的图象位置，画出图象，直接判断交点个数．【详解】若二次函数的图象在第三、四象限，开口向下，顶点在原点，y 轴是对称轴；反比例函数的图象在第一，三象限，故两个函数的交点只有一个，在第三象限．同理，若二次函数的图象在第三、四象限，开口向下，顶点在原点，y 轴是对称轴；反比例函数的图象在第二，四象限，故两个函数的交点只有一个，在第四象限．故答案为：B ．【点睛】本题考查了二次函数和反比例函数的图象问题，掌握二次函数和反比例函数的图象性质是解题的关键．18．在平面直角坐标系中，点P 的坐标为()1,2，将抛物线21322y x x =-+沿坐标轴平移一次，使其经过点P ，则平移的最短距离为（ ）A ．12B ．1C ．5D ．52【答案】B【解析】【分析】先求出平移后P 点对应点的坐标，求出平移距离，即可得出选项．【详解】 解：21322y x x =-+=()215322x --， 当沿水平方向平移时，纵坐标和P 的纵坐标相同，把y=2代入得：解得：x=0或6，平移的最短距离为1-0=1；当沿竖直方向平移时，横坐标和P 的横坐标相同，把x=1代入得：解得：y=12-， 平移的最短距离为152=22⎛⎫--⎪⎝⎭， 即平移的最短距离是1，故选B.【点睛】本题考查了二次函数图象上点的坐标特征，能求出平移后对应的点的坐标是解此题的关键．19．平移抛物线y ＝﹣（x ﹣1）（x +3），下列哪种平移方法不能使平移后的抛物线经过原点（ ）A ．向左平移1个单位B ．向上平移3个单位C ．向右平移3个单位D ．向下平移3个单位【答案】B【解析】【分析】先将抛物线解析式转化为顶点式，然后根据顶点坐标的平移规律即可解答.【详解】解：y ＝﹣（x ﹣1）（x +3）=-（x+1）2+4A 、向左平移1个单位后的解析式为：y ＝-（x+2）2+4，当x=0时，y=0，即该抛物线经过原点，故本选项不符合题意；B 、向上平移3个单位后的解析式为：y=-（x+1）2+7，当x=0时，y=3，即该抛物线不经过原点，故本选项符合题意；C 、向右平移3个单位后的解析式为：y=-（x-2）2+4，当x=0时，y=0，即该抛物线经过原点，故本选项不符合题意.；D 、向下平移3个单位后的解析式为：y=-（x+1）2+1，当x=0时，y=0，即该抛物线经过原点，故本选项不符合题意.【点睛】本题考查了二次函数图像的平移，函数图像平移规律：上移加，下移减，左移加，右移减.20．在同一坐标系中，二次函数2y ax bx =+与一次函数y bx a =-的图像可能是（ ） A ． B ．C ．D ．【答案】C【解析】【分析】直线与抛物线联立解方程组，若有解，则图象有交点，若无解，则图象无交点；根据二次函数的对称轴在y 左侧，a ，b 同号，对称轴在y 轴右侧a ，b 异号，以及当a 大于0时开口向上，当a 小于0时开口向下，来分析二次函数；同时在假定二次函数图象正确的前提下，根据一次函数的一次项系数为正，图象从左向右逐渐上升，一次项系数为负，图象从左向右逐渐下降；一次函数的常数项为正，交y 轴于正半轴，常数项为负，交y 轴于负半轴．如此分析下来，二次函数与一次函数无矛盾者为正确答案．【详解】解：由方程组2y ax bx y bx a⎧=+⎨=-⎩得ax 2＝−a ， ∵a ≠0∴x 2＝−1，该方程无实数根，故二次函数与一次函数图象无交点，排除B ．A ：二次函数开口向上，说明a ＞0，对称轴在y 轴右侧，则b ＜0；但是一次函数b 为一次项系数，图象显示从左向右上升，b ＞0，两者矛盾，故A 错；C：二次函数开口向上，说明a＞0，对称轴在y轴右侧，则b＜0；b为一次函数的一次项系数，图象显示从左向右下降，b＜0，两者相符，故C正确；D：二次函数的图象应过原点，此选项不符，故D错．故选C．【点睛】本题考查的是同一坐标系中二次函数与一次函数的图象问题，必须明确二次函数的开口方向与a的正负的关系，a，b的符号与对称轴的位置关系，并结合一次函数的相关性质进行分析，本题中等难度偏上．。

一、二次函数 真题与模拟题分类汇编（难题易错题） 1．已知抛物线26y x x c =-++.（1）若该抛物线与x 轴有公共点，求c 的取值范围；（Ⅱ）设该抛物线与直线21y x =+交于M ，N 两点，若MN =C 的值； （Ⅲ）点P ，点Q 是抛物线上位于第一象限的不同两点，,PA QB 都垂直于x 轴，垂足分别为A ，B ，若OPA OQB ∆≅∆，求c 的取值范围.【答案】（I ）9c -；（Ⅱ）2c =-；（Ⅲ）c 的取值范围是2174c -<< 【解析】 【分析】(1) 抛物线与x 轴有公共点，则判别式为非负数，列不等式求解即可;(2)求出二次函数与直线的交点，并根据勾股定理求出MN 的长度，列方程即可求解; (3)由OPA OQB ∆≅∆可知，P ,Q 两点的坐标特点，设坐标得到设点P 的坐标为(, )m n ，则点Q 的坐标为(,)n m ，代入二次函数，得到n,m 的关系，则只需保证该方程有正根即可求解. 【详解】解：（I ）∵抛物线26y x x c =-++与x 轴有交点，∴一元二次方程260x x c -++=有实根。

240b ac ∴∆=-，即264(1)0c -⨯-⨯.解得9c -（Ⅱ）根据题意，设()()1122,21,,21M x x N x x ++由2621y x x c y x ⎧=-++⎨=+⎩，消去y ，得2410x x c -+-= ①. 由2(4)4(1)1240c c ∆=---=+>，得3c >-.∴方程①的解为1222x x ==()()()()22221212122121520(3)MN x x x x x x c ∴=-++-+=-=+⎡⎤⎣⎦ 20(3)20c ∴+=，解得2c =-（Ⅲ）设点P 的坐标为(, )m n ，则点Q 的坐标为(,)n m ，且0,0,m n m n >>≠，2266m m c n n n c m⎧-++=∴⎨-++=⎩，两式相减，得227()0n m m n -+-=，即()(7)0m n m n -+-= 7m n ∴+=，即7n m =-2770m m c ∴-+-=，其中07m <<由0∆，即274(1)(7)0c -⨯-⨯-，得214c -.当214c =-时，72m n ==，不合题意。