下载文档原格式
交巡警服务平台的设置与调度摘要本文是在一个原有区域交警平台的基础上，分析讨论在该市警务资源有限的情况下，如何实现城市的实际情况与需求合理地设置交巡警服务平台、分配各平台的管辖范围、调度警务资源的实际问题。
实现最优化管理的方案。
以图论最优路径理论为基础，建立图的最优化模型。
针对问题（1），将A区路口和道路抽象成图，分别以交巡警服务平台对应的点为起点求小于等于3min的路径，再将同一起点的路径的终点相连，围成一个区域，便是交巡警服务平台的管辖范围。
在此基础上综合考虑各个路口发案率的大小、区域人口密集程度，从而建立一个图中路径最优化模型。
再根据各个区域之间的所产生的空白区，即交巡警的管辖盲区。
为其添加交巡警服务平台。
实现其管理最优化的目的。
针对问题（2），结合交巡警服务平台的设置原则，充分考虑全市各区不同的状况，如：人口密度、区域面积等，并以A区的分区标准为基础，实现对全市各区的交巡警服务平台的设置。
对于P点的逃犯，建立一个以P点为中心的最优逃跑路径所组成的图，然后在算出罪犯的最佳逃跑路线，再调度相应的交巡警，实现对他的围堵。
从而实现交巡警服务平台设置和调度的最优化的方案。
关键词：图论;最优化路径; 交巡警服务平台；MATLAB；数据结构1、问题重述“有困难找警察”，是家喻户晓的一句流行语。
警察肩负着刑事执法、治安管理、交通管理、服务群众四大职能。
为了更有效地贯彻实施这些职能，需要在市区的一些交通要道和重要部位设置交巡警服务平台。
每个交巡警服务平台的职能和警力配备基本相同。
由于警务资源是有限的，如何根据城市的实际情况与需求合理地设置交巡警服务平台、分配各平台的管辖范围、调度警务资源是警务部门面临的一个实际课题。
试就某市设置交巡警服务平台的相关情况，建立数学模型分析研究下面的问题：（1）附件1中的附图1给出了该市中心城区A的交通网络和现有的20个交巡警服务平台的设置情况示意图，相关的数据信息见附件2。
请为各交巡警服务平台分配管辖范围，使其在所管辖的范围内出现突发事件时，尽量能在3分钟内有交巡警（警车的时速为60km/h）到达事发地。
交巡警服务平台的设置与调度
按照功能划分，城区一般可分为生活区、工业区、山区、主干道路区及公园绿地区等，分别记为1类区、2类区、……、5类区，不同的区域环境受人类活动影响的程度不同。
现对某城市城区土壤地质环境进行调查。
为此，将所考察的城区划分为间距1公里左右的网格子区域，按照每平方公里1个采样点对表层土（0~10 厘米深度）进行取样、编号，并用GPS记录采样点的位置。
应用专门仪器测试分析，获得了每个样本所含的多种化学元素的浓度数据。
另一方面，按照2公里的间距在那些远离人群及工业活动的自然区取样，将其作为该城区表层土壤中元素的背景值。
附件1列出了采样点的位置、海拔高度及其所属功能区等信息，附件2列出了8种主要重金属元素在采样点处的浓度，附件3列出了8种主要重金属元素的背景值。
现要求你们通过数学建模来完成以下任务：
(1) 给出8种主要重金属元素在该城区的空间分布，并分析该城区内不同区域重金属的污染程度。
(2) 通过数据分析，说明重金属污染的主要原因。
(3) 分析重金属污染物的传播特征，由此建立模型，确定污染源的位置。
(4) 分析你所建立模型的优缺点，为更好地研究城市地质环境的演变模式，还应收集什么信息？有了这些信息，如何建立模型解决问题？。
交巡警服务平台的设置与调度优化分析摘要本文综合应用了Floyd算法，匈牙利算法，用matlab计算出封锁全市的时间为1.2012小时。
并在下面给出了封锁计划。
为了得出封锁计划，首先根据附件2的数据将全市的道路图转为邻接矩阵，然后根据邻接矩阵采用Floyd算法计算出该城市任意两点间的最短距离。
然后从上述矩阵中找到各个交巡警平台到城市各个出口的最短距离，这个最短距离矩阵即可作为效益矩阵，然后运用匈牙利算法，得出分派矩阵。
根据分派矩阵即可制定出封锁计划：96-151,99-153,177-177,175-202,178-203,323-264,181-317, 325-325,328-328，386-332,322-362,100-387,379-418,483-483, 484-541,485-572。
除此以外，本人建议在编号为175的路口应该设置一个交巡警平台，这样可以大大减少封锁全市的时间，大约可减少50%。
关键词: Floyd算法匈牙利算法 matlab一、问题重述“有困难找警察”，是家喻户晓的一句流行语。
警察肩负着刑事执法、治安管理、交通管理、服务群众四大职能。
为了更有效地贯彻实施这些职能，需要在市区的一些交通要道和重要部位设置交巡警服务平台。
每个交巡警服务平台的职能和警力配备基本相同。
由于警务资源是有限的，如何根据城市的实际情况与需求合理地设置交巡警服务平台、分配各平台的管辖范围、调度警务资源是警务部门面临的一个实际课题。
试就某市设置交巡警服务平台的相关情况，建立数学模型分析研究下面的问题：警车的时速为60km/h, 现有突发事件，需要全市紧急封锁出入口，试求出全市所有的交巡警平台最快的封锁计划，一个出口仅需一个平台的警力即可封锁。
二、模型假设1、假设警察出警时的速度相同且不变均为60/km h 。
2、假设警察出警的地点都是平台处。
3、假设警察接到通知后同时出警，且不考虑路面交通状况。
三、符号说明及一些符号的详细解释A 存储全市图信息的邻接矩阵 D 任意两路口节点间的最短距离矩阵X 01-规划矩阵ij a ,i j 两路口节点标号之间直达的距离 ij d 从i 路口到j 路口的最短距离 ij b 从i 号平台到j 号出口的最短距离ij x 取0或1，1ij x =表示第i 号平台去封锁j 号出口在本文中经常用到,i j ，通常表示路口的编号，但是在ij d ，ij b ，ij x 不再表示这个意思，i 表示第i 个交巡警平台，交巡警平台的标号与附件中给的略有不同，如第21个交巡警平台为附件中的标号为93的交巡警平台，本文的标号是按照程序的数据读取顺序来标注的，在此声明；j 表示第j 个出口，如：第5个出口对应于附件中的路口编号为203的出口。
全国大学生数学建模竞赛承诺书我们仔细阅读了中国大学生数学建模竞赛的竞赛规则.我们完全明白，在竞赛开始后参赛队员不能以任何方式（包括电话、电子邮件、网上咨询等）与队外的任何人（包括指导教师）研究、讨论与赛题有关的问题。
我们知道，抄袭别人的成果是违反竞赛规则的,如果引用别人的成果或其他公开的资料（包括网上查到的资料），必须按照规定的参考文献的表述方式在正文引用处和参考文献中明确列出。
我们郑重承诺，严格遵守竞赛规则，以保证竞赛的公正、公平性。
如有违反竞赛规则的行为，我们将受到严肃处理。
我们参赛选择的题号是（从A/B/C/D中选择一项填写）：B我们的参赛报名号为（如果赛区设置报名号的话）：所属学校（请填写完整的全名）：西北大学参赛队员(打印并签名)：1.张舒岱2.刘羽3.张成悟指导教师或指导教师组负责人(打印并签名)：日期：2014年8月10日全国大学生数学建模竞赛编号专用页赛区评阅编号（由赛区组委会评阅前进行编号）：全国评阅编号（由全国组委会评阅前进行编号）：交巡警服务平台的设置与调度摘要交巡警服务平台位置的选取以及划分交巡警服务平台的管辖范围对于处理突发事件有非常大的影响。
现阶段，一般依据经验选取服务平台位置及划分管辖区域。
所以如何科学合理处理的交巡警服务平台的设置与调度问题具有十分重要的现实意义。
本文研究了交巡警服务平台的设置与调度问题。
具体讨论了在给定的区域A内，如何合理的设置交巡警服务平台的管辖区域；发生特殊事件时应如何调动服务平台警力以快速封锁区域A；应该增加多少数量交巡警服务平台以及在哪个位置增加。
本文建立最短路模型、0-1整数规划模型，利用MATLAB软件解决了分配各平台管辖范围、调度警务资源以及合理设置交巡警服务平台这三个方面的问题。
在解决分配各平台管辖范围问题时，本文建立了最短路模型。
通过求解各个路口到交巡警平台的距离是否满足最低时间限制，解决交巡警服务平台分配管辖范围的问题。
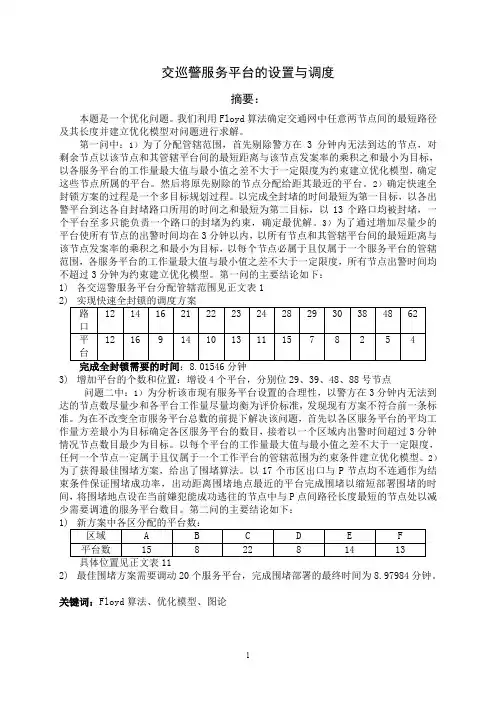
本文在MATLAB软件上运用Dijkstra算法进行求解，给出了中心城区A的20个服务平台的管辖范围，并求得到达最近的交巡警服务平台的时间超过3分钟的6个路口。
交巡警服务平台的设置和调度摘要本文针对交巡警服务平台的设置和调度问题，通过题目给出的全市交通信息，采用弗洛伊德算法思想、借助矩阵、MATBLE和LINGO软件，求出最短距离矩阵和最短路径矩阵，再过数据的分析、筛选和计算，将目标函数进行优化。
针对A区问题一：根据最短路径原则，利用弗洛伊德算法计算A区92个路口任意两个之间的最短路径距离。
首先，根据距离最短原则建立数学模型，即根据最短路径进行分配；其次，对模型进行优化，对模型增加各平台的工作量，即为平台到节点的距离和该节点的案发频率的乘积。
为使达到相对工作量均衡（大于10的即为不公平），将其大于10的进行调整。
针对A区问题二：将问题转化为求所有方案中到达指定A区出入口路径最长的交巡警平台的最小值问题，建立目标规划模型，即对13个出入A区的节点实现最短时间封锁，同时一个交巡警服务平台只能封锁一个出入路口。
运用LINGO 程序，进行求解，最优解为Km。
MIN0155.8针对A区问题三：对于该问题主要总结上面两小问，在满足各交巡警服务平台到达各管辖节点最长时间小于三分钟且工作量相对均衡下，求交巡警服务平台增加数的最小值。
建立在符合相应约束条件求最小值的线性规划问题，求得最优解为新增四个交巡警服务平台。
关键词Floyd算法整体规划优化决策问题重述为了有效地贯彻实施警察刑事执法、治安管理、交通管理、服务群众的职能，需要在市区的一些交通要道和重要部位设置交巡警服务平台，且各职能和警力配备基本相同。
警务资源是有限的，问题在于根据城市的实际情况与需求合理地设置交巡警服务平台、分配各平台的管辖范围、调度警务资源。
1.中心城区A要解决的问题（1）根据题目给出的各附表，为各交巡警服务平台分配管辖范围，使其在所管辖的有突发事件尽量能在三分钟内到达。
（2）调度全区20个交巡警服务平台的警力资源，对进出该区的13条范围内出现突发事件时，要道实现快速全封锁。
设计该区交巡警服务平台警力合理的调度方案。
交巡警服务平台的设置与调度作者：来志强于德恩孟利丹来源：《科技创新导报》 2012年第16期来志强于德恩孟利丹(河海大学力学与材料学院河南 210000)摘要:本文以2011年全国大学生数学建模竞赛B题为背景,主要解决如何根据城市的实际情况与需求合理地设置交巡警服务平台、分配各平台的管辖范围、调度警务资源等问题。
关键词:离散化 0—1规划引力场无约束多目标规划预备集中图分类号:C916 文献标识码:A 文章编号:1674-098X(2012)06(a)-0249-01首先对城市坐标图所有道路以一定单位长度为间距进行离散化。
针对问题1.1,利用就近原则方法建立就近区域模型,得到各个平台所管辖的区域,3min内到达的覆盖率,所有平台中到达所管辖区域内最远点的最长时间。
针对问题1.2,通过0—1规划和Floyd算法,建立极小极大模型,并进行求解优化,得到平台警力合理的调度方案,所有警力到达相应进区路口时所需的时间和最短总路程。
针对问题1.3,通过案发率、最短距离,两个指标加权构造引力因子,建立了引力场模型,最后最佳的调整方案针对问题1.2,在原有平台位置不变的情况下,考虑增加平台后,通过引力场方法,得到相应各区的前后目标对比值表,从而可以得到各平台的调整情况。
1 问题分析利用计算机求解得到各个平台的,通过对其数值分析,可以确定加4个平是最优方案。
3 预备集模型及定义嫌疑犯在3分钟后开始逃跑,下一次可参考文献[1]姜启源.数学模型[M].北京.高等教育出版社.1993.[2]赵静.数学建模与数学实验(第3版).北京.高等教育出版社2010年8月.[3]吴孟达,王丹.“110警车配置及巡逻方案”评阅综述.北京.选自数学的实践与认识期刊第40卷第15期,2010年8月.。
交巡警服务平台的设置与调度——云南师范大学 谭海云马 娟陈久毅摘要本文可分为五大问题，第一问首先通过用Matlab 软件把各线段的距离求出并标出92个交叉路口所对应的编号，由交巡警服务平台的原则：快速处警原则——城区接警后确保快速到达现场。
可知，所有的92个路口都应该属于距离它们最近的交巡警服务平台的管辖范围，然后用图论中的Dijkstra 矩阵算法，找出距离各个交叉路口最近的交巡警服务平台，建立了到达最远且用时最短的模型，及在最小的响应时间范围内，到达需求点所配备的服务平台数量最少，由此，建立了0-1规划模型。
结果发现，大多数交叉路口突发事件发生时，三分钟之内，都有交巡警到达事发点，只有28、29、38、39、61、92六个路口在事发三分钟内没有交巡警到达，但最长时间也只要5分36秒，比较合理。
第二个问题中，要调动全区的服务台来封锁交通要道，涉及到每个服务台的出警时间和工作量的不均衡。
于是，本文建立以最大相应量最小原则建立了责任划分模型，使得各个 服务区的工作量不是很大。
在第一个问题中，按交巡警服务平台的快速处警原则可以发现各个交警服务平台的负荷不平衡，而且有的交叉路口处案发率不同。
所以，第三个问题中可通过各个交巡警服务平台所管辖的路口平均每天的案发次数，结合A 区地图，分别假设交巡警服务平台可迁移和不可迁移的不同情况，分别可增加3个或者5个服务平台，使得每个交巡警服务平台所管辖的范围内平均每天的案发次数大多都在4—6次之间，且在遇突发事件的时候，几乎都能在3分钟之内到达。
第四个问题，我们根据A 、B 、C 、D 、E 、F 各个区域的平均每天案发次数和人口密度所占该市的比率12i i γγ和，通过定义一个指标——交警服务率：12(1)i i γαγαγ=+-来将80个交巡警服务平台重新分配到不同的区域，其中，权重α是已知的，且在不同人心目中的值不同。
经过计算人口密度的时候发现，A 区平均人口密度过大，达到2.72万人/平方千米。
2011高教社杯全国大学生数学建模竞赛题目（请先阅读“全国大学生数学建模竞赛论文格式规范”）题目B题交巡警服务平台的设置与调度摘要：本文研究的是某城区警车配置及巡逻方案的制定问题，建立了求解警车巡逻方案的模型，并在满足D1的条件下给出了巡逻效果最好的方案。
在设计整个区域配置最少巡逻车辆时，本文设计了算法1：先将道路离散化成近似均匀分布的节点，相邻两个节点之间的距离约等于一分钟巡逻路程。
由警车的数目m,将全区划分成m个均匀的分区，从每个分区的中心点出发，找到最近的道路节点，作为警车的初始位置，由Floyd算法算出每辆警车3分钟或2分钟行驶路程范围内的节点。
考虑区域调整的概率大小和方向不同会影响调整结果，本文利用模拟退火算法构造出迁移几率函数，用迁移方向函数决定分区的调整方向。
计算能满足D1的最小车辆数，即为该区应该配置的最小警车数目，用MATLAB计算，得到局部最优解为13辆。
在选取巡逻显著性指标时，本文考虑了两个方面的指标：一是全面性，即所有警车走过的街道节点数占总街道节点数的比例，用两者之比来评价；二是均匀性，即所有警车经过每个节点数的次数偏离平均经过次数的程度，用方差值来大小评价。
问题三：为简化问题，假设所有警车在同一时刻，大致向同一方向巡逻，运动状态分为四种：向左，向右，向上，向下，记录每个时刻，警车经过的节点和能够赶去处理事故的点，最后汇总计算得相应的评价指标。
在考虑巡逻规律隐蔽性要求时，文本将巡逻路线进行随机处理，方向是不确定的，采用算法2进行计算，得出相应巡逻显著指标，当车辆数减少到10辆或巡逻速度变大时，用算法2计算巡逻方案和对应的参数，结果见附录所示。
本文最后还考虑到4个额外因素，给出每个影响因素的解决方案。
关键词：模拟退火算法；Floyd算法；离散化一问题的重述110警车在街道上巡逻，既能够对违法犯罪分子起到震慑作用，降低犯罪率，又能够增加市民的安全感，同时也加快了接处警时间，提高了反应时效，为社会和谐提供了有力的保障。
现给出某城市内一区域，其道路数据和地图数据已知，该区域内三个重点部位的坐标分别为：（5112，4806），（9126， 4266），（7434 ，1332）。
该区域内共有307个道路交叉口，为简化问题，相邻两个交叉路口之间的道路近似认为是直线，且所有事发现场均在下图的道路上。
该市拟增加一批配备有GPS卫星定位系统及先进通讯设备的110警车。
设110警车的平均巡逻速度为20km/h，接警后的平均行驶速度为40km/h。
警车配置及巡逻方案要尽量满足以下要求：D1. 警车在接警后三分钟内赶到现场的比例不低于90％；而赶到重点部位的时间必须在两分钟之内。
D2. 使巡逻效果更显著；D3. 警车巡逻规律应有一定的隐蔽性。
现在我们需要解决以下几个问题：一. 若要求满足D1,该区最少需要配置多少辆警车巡逻？二. 请给出评价巡逻效果显著程度的有关指标。
三．请给出满足D1且尽量满足D2条件的警车巡逻方案及其评价指标值。
四. 在第三问的基础上，再考虑D3条件，给出你们的警车巡逻方案及其评价指标值。
五．如果该区域仅配置10辆警车，应如何制定巡逻方案，使D1、D2尽量得到满足？六. 若警车接警后的平均行驶速度提高到50km/h，回答问题三。
七. 你们认为还有哪些因素、哪些情况需要考虑？给出你们相应的解决方案。
二问题分析本题为城区道路网络中警车配置及巡逻问题。
在进行警车配置时，首先要考虑警车在接警后在规定时间内赶到现场的比例，在此条件下，以车数最少为目标，建模、求解；在制定巡逻方案时，要考虑巡逻的效果及隐蔽性问题。
问题一只要求满足D1，求最少的警车配置数，可以认为警车是不动的，在三分钟或两分钟内它能到达的区域就是它的覆盖范围。
据此，在满足所有街道的覆盖率不低于90%的条件下，寻找最优解。
问题二要评价巡逻效果，有两个方面需要考虑：一是巡逻的全面性，即经过一段时间后警车走过的街道数占总街道数的比例；二是巡逻的不均匀性，即经过一段时间后警车经过每一条街道的次数相差不大，用方差来衡量。
问题三是在满足D1的条件上尽量满足问题二所给的指标，并给出评价方案的指标。
首先找到一组满足D1的各警车位置，然后在和各警车位置相连的点中随机寻找一个点，判断新的点是否满足D1，如果满足则警车行驶到该点，否则重新寻找，直到满足为止。
一段时间后统计所有车走过的点数及每个点被走过的次数，用问题二给出的两个指标进行评价。
综合两个指标，可判断此路径的好坏，重复这个过程，直到综合评价指标达到一个满意的值为止。
问题四增加了隐蔽性要求，首先给出评价隐蔽性的指标，隐蔽性可用路线的随机性来评价，将它加入到问题三的模型中去进行求解。
问题五限制警车数量为10，要综合考虑D1、D2，先分配这10辆车使道路的覆盖率最高，然后按照问题三的步骤进行求解，其中每一步对D1的判断只需使道路的覆盖率尽量高即可。
问题六同问题三，只需将车速改为50km/h即可。
三模型的假设1.警车都在路上巡逻，巡警去处理案件的时间不考虑；2.所有事发现场都在道路上，案件在道路上任一点是等概率发生的；3.警车初始停靠点是随机的，但尽量让它们分散分布，一辆警车管辖一个分区；4.假定各个划分区域内，较短时间内，最多会发生一个案件；5.假设区域内的每条道路都是双行线，不考虑转弯对结果造成的影响；6.如果重点部位不在道路上的，假设这些重点部位在离它们最近的道路上；7. 图中水域对巡逻方案没有影响。
四符号说明m表示警车数目d表示警车初始停靠点到各道路的最短距离L表示整个区域的总道路长度l表示不能在3分钟内到达的区域的道路的长度k表示非重点部位的警车在3分钟内不能到达现场的比例r表示三分钟内能从接警位置赶到事发现场的最大距离是n表示整个区域总的离散点个数n表示第i区内的节点个数if表示区内调整函数1t表示模拟退火的时间，表征温度值f表示区间调整函数2r表示全面性指标e表示不均匀性指标h表示综合评价指标s表示第i辆车经过每条道路的次数is表示整个区域每条道路经过的平均次数五 模型的建立与算法的设计5.1 满足D1时，该区所需要配置的最少警车数目和巡逻方案5.1.1 满足D1条件时，区域最少警车的规律题目要求警车的配置和巡逻方案满足D1要求时，整个区域所需要配置的警车数目最少。
由假设可知警车都在道路上，且所有事发现场也都在道路上，但区域内总的道路长度是个定值的；警车在接警后赶到事发现场有时间限制和概率限制：三分钟内赶到普通区域案发现场的比例不低于90％，而赶到重点部位的时间必须控制在两分钟之内。
由此可知每辆警车的管辖范围不会很大，于是考虑将整个区域分成若干个分区，每辆警车管辖一个分区域。
由上面的分析，求解整个区域的警车数目最少这个问题可转化为求解每一辆警车所能管辖的街道范围尽量的大。
于是我们寻找出使每辆警车管辖的范围尽量大的规律。
为了简化问题，我们不考虑赶到现场的90%的几率的限制，仅对警车能在三分钟内赶到事发现场的情况作定性分析，其分析示意图如图1所示。
警车的初始停靠位置是随机的分布在道路上的任一节点上，我们假设一辆警车停靠在A 点上。
图1 一辆警车管辖范围分析示意图由于警车的平均巡逻速度为20km/h ，接警后的平均行驶速度为40km/h ，由于距离信息比较容易得到，于是我们将时间限制转化为距离限制，这样便于分析和求解。
当警车接警后，在三分钟内能从接警位置赶到事发现场的最大距离是r ，其中km r 240603=⨯=。
如图1所示，我们设警车初始停靠位置在A 点，A 点是道路1，2，3，4的道路交叉口。
我们仅以警车在道路1巡逻为例来进行分析，警车以h km /20的速度在道路1上A 到'A 点之间巡逻，'A 与初始停靠点A 的距离为xkm 。
由于案件有可能在道路上任一点发生，当警车巡逻到A点时，若案发现场在道路2，3，4上发生时，警车以40km/h的速度向事发现场行驶，警车能在三分钟内从'A点赶到现场的最大距离为km2(-。
如x)果警车在道路1上继续向前行驶，则该警车能在三分钟内赶到现场的距离继续缩小，当警车从初始点向A点行驶但没有达到'A点时，此时该警车的最大管辖范围比警车到达'A 点时的最大管辖范围大。
为了使警车的管辖范围尽量大，警车的巡逻范围越小越好，当2。
x时，即警车在初始停靠点静止不动时，警车的管辖范围达到最大值km 0=图1所分析的是特殊的情况，道路1，2，3，4对称分布，现在我们来对一般的情况进行分析，如图2所示。
图2.1 图2.2图2 一辆警车最大管辖范围分析示意图图2.1所示的情况是道路分布不对称，与图1相比，图2.1所示的道路方向和角度都发生了改变，图2.3中的情形更为复杂。
参照对图1的分析方法，我们分析这两种情形下，警车巡逻时能在三分钟内赶到现场的最大距离的规律，我们只分析图2.2的情况，道路1，2，3，4，5相交于点C,同时道路1与道路6也有个道路交叉口D，由于警车巡逻时是在道路上行驶的，行走的路线是分段直线,并不影响路径的长度，所以当警车巡逻到距离初始停靠点C点x远处的D，此时若有案件发生时，该警车要在三分钟内能赶到现场处理案件，最大行驶距离在km2(-之内，如果警车在道路1上继续向前行驶，x)则该警车能在三分钟内赶到现场的距离继续缩小，当警车没有行驶到D点时，此时该警车的最大管辖范围比km2(-大，为了使警车的管辖范围尽量大，警车的巡逻范围越小x)越好。
当0x时，即警车静止不动时，一辆警车的管辖范围能达到最大值。
=以上分析的仅作定性的分析，对于三个重点部位也可以同理分析，所得的结论是一致的，以上的分析没有考虑到90%的到达几率限制，但在设计算法需要充分考虑。
综上所述，当警车静止在初始停靠点时，在三分钟时间限制内，警车能从初始停靠点赶到事发现场的最大距离为km2。
5.1.2 将道路离散化由于事发现场是等概率地分布在道路上的，由区域地图可以发现，整个区域中的道路长度不均，为了使计算结果更加精确，可将这些道路离散化。
只要选取合适的离散方案，就能使警车在经过道路上的离散的点时就相当于经过了这条道路。
这样，不论是求解警车初始停靠点还求解警车赶到事发现场所经过的道路时，所计算得的的结果显然比仅考虑整条道路的叉路口要精确得多。
区域中共有307个道路交叉口，458条道路。
我们采用线性插值方法对道路进行离散化，以h km /20的速度行走一分钟的距离作为步长，一分钟时间的选择是参照问题三的结果要求来设定的，步长km b 3120601=⨯=。
用线性插值的方法，从道路的一个方向进行线性插值，实现将每条道路离散化的目标，考虑到有些道路不是km 31的整数倍，我们就一般情况进行讨论，其分析示意图如图3所示。
